基于奇异摄动法的固定翼无人机优化PID 控制①
朱涵智 梅 平 刘云平 赵中原 张婷婷
(南京信息工程大学自动化学院 南京210044)
(陆军工程大学指挥控制工程学院 南京210017)
0 引言
固定翼无人机(unmanned aerial vehicle,UAV)因其巡航时间长、飞行范围广、使用成本低、信息感知率强等优势,被广泛运用于巡逻侦察、电子干扰、战场支援、森林灭火以及地形绘制等军民用领域。由于以上优点,固定翼无人机被普遍认为是未来信息化发展的重要平台。然而,不同于旋翼无人机运动模型,固定翼无人机是典型的具有非完整线性约束的运动体,其动力学模型具有阶次高、非线性强等特性,且存在最大、最小空速以及最大航向角速度等的限制[1],同时风速的干扰是随机和时变的,对于不同重量和不同重心的固定翼无人机,飞行姿态与速度的控制效果也不尽相同,因此,固定翼无人机的控制相较于旋翼等其他无人机控制更为复杂,控制难度也更大。采用奇异摄动法能够降低系统阶次、消除系统刚性问题。同时由于奇异摄动法的基础是系统的时间尺度特性,因此它能够同时适用于线性及非线性系统[2]。
目前,固定翼无人机控制方法主要有比例积分微分(proportional integral derivative,PID)控制[3-4]、自适应控制[5]、鲁棒控制[6]以及多种控制方法融合等。对于固定翼飞行策略优化控制问题,众多国内外优秀学者都有不同的见解、设计与实践。王力等人[7]在设计固定翼控制方法时,引入了非线性干扰观测器对复合干扰进行精确估计,同时设计自适应二阶PID 滑模控制器消除了切换控制引起的抖震现象。宗群等人[5]针对固定翼无人机的姿态和速度控制中存在不确定和外部扰动的问题,设计自适应超螺旋滑模干扰观测器和控制器,从而实现固定翼无人机对速度和姿态命令的有限时间精确跟踪。Raza[8]等人利用输出反馈控制拓扑为非线性固定翼模型设计鲁棒控制器并且引入不确定性对控制器和观测器的鲁棒性进行了评估。以上各飞行优化方法使得固定翼无人机在有外部气体扰动的情况下的飞行姿态和速度控制响应时间和鲁棒性有了很大的提高。然而,由于固定翼控制器的设计复杂性,上述优化控制方法很难应用于实际飞行,当前应用较为广泛的仍为传统PID 控制器,因此,本文在传统PID 控制上采用奇异摄动方法进行优化,以提高系统的响应速度和稳定性。
在系统理论与控制工程中,建模是一个基本问题。多数物理系统都含有快、慢动态耦合的现象。早期对这类系统的处理方法是简单地忽略快变模态从而降低系统的阶数,然而,大量事实证明,基于这样的简化模型设计的控制效果往往与设计要求相距甚远。奇异摄动方法是有效处理这类问题的工具。其思想是首先忽略快变量以降低系统阶数,然后通过引入边界层校正来提高近似程度。这两个降阶的系统就可以用来近似原系统的动力学行为。文献[9]指出在飞机的姿态控制中,角速度的变化远远快于速度和角度,可以考虑将此类系统建为奇异摄动模型。
针对传统PID 控制无法使固定翼无人机达到较好的控制效果,使用奇异摄动法进行固定翼无人机PID 优化控制率设计。仿真结果表明,相较于传统PID 控制方法,采用奇异摄动法进行快慢分解的双闭环PID 控制器能够保证线速度等慢变量响应不变情况下,大大提高角速度等快变量的响应时间,更快达到期望控制量。
1 固定翼无人机奇异摄动系统建模
1.1 坐标系的建立与变换
运动中的固定翼飞机,其运动方程可以用独立的一阶常微分方程组表示。由于方程组中包含相关的空气动力、转动惯量等因素,纵向、横向和航向的运动之间会发生耦合,为了有效地分离耦合变量且简化非线性方程组,建立合适的坐标系是极其必要的。
为了描述固定翼无人机的速度和姿态变化,本文采用地面坐标系和机体坐标系来描述无人机的飞行状态,并给出相应的变换矩阵。
在地面上选一点为地面坐标系原点O,OR轴指向正北,OS轴指向正东并在地面上与OR轴垂直,OT轴指向地心且与面ORT垂直,符合右手坐标系。机体坐标系原点o位于固定翼无人机质心处,ox轴指向固定翼机头方向,oy轴垂直于ox轴指向飞机右侧,oz轴垂直于oxy轴指向固定翼机腹,为右手坐标系。坐标系示意图如图1 所示。
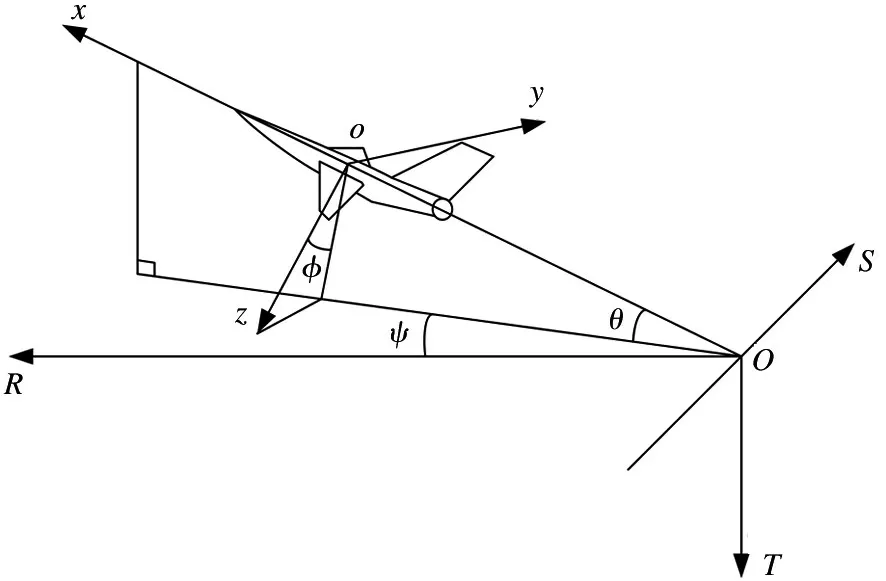
图1 坐标系示意图
为建立固定翼无人机模型,现将各方向运动由参数表示,参数及其含义见表1。

表1 机体坐标系下运动参数及其含义
同时,固定翼无人机的运动姿态和位置也能够由地面坐标系相对于机体坐标系的角度变化和坐标来确定。在地面坐标系下固定翼无人机的各参数及其含义见表2。

表2 地面坐标系下运动参数
1.2 固定翼无人机动力学建模
为减少不必要的干扰,简化无人机运动学方程推导,本文将做出如下假设。
(1) 飞机为刚体,不会出现弹性形变,机身任意两点距离相对不变,飞行时不受到外界干扰。
(2) 惯量积为0。
(3) 忽略地球自转对飞机的影响,且重力加速度g不随着飞机运动而改变。
可将非线性固定翼运动方程描述为
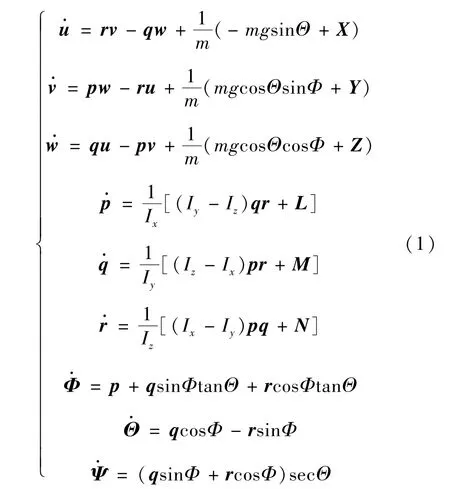
采用小扰动理论[10]可将方程组线性化处理,其理论简化步骤如下。
(1) 将式(1)中所有变量表示为基准值与扰动值之和,对于构造对称的飞机在水平飞行无干扰情况下,设定横、航向基准值为0。
(2) 选定无角速度的对称基准飞行状态(水平飞行),使得v0=w0=p0=q0=r0=Φ0=0,并定义u0为基准的飞行速度,θ0为航迹角。
(3) 假设所有干扰量都很小,其时间导数也很小。角度余弦值可视为1,正弦值为0。
可获得以扰动增量为变量的线性方程组:
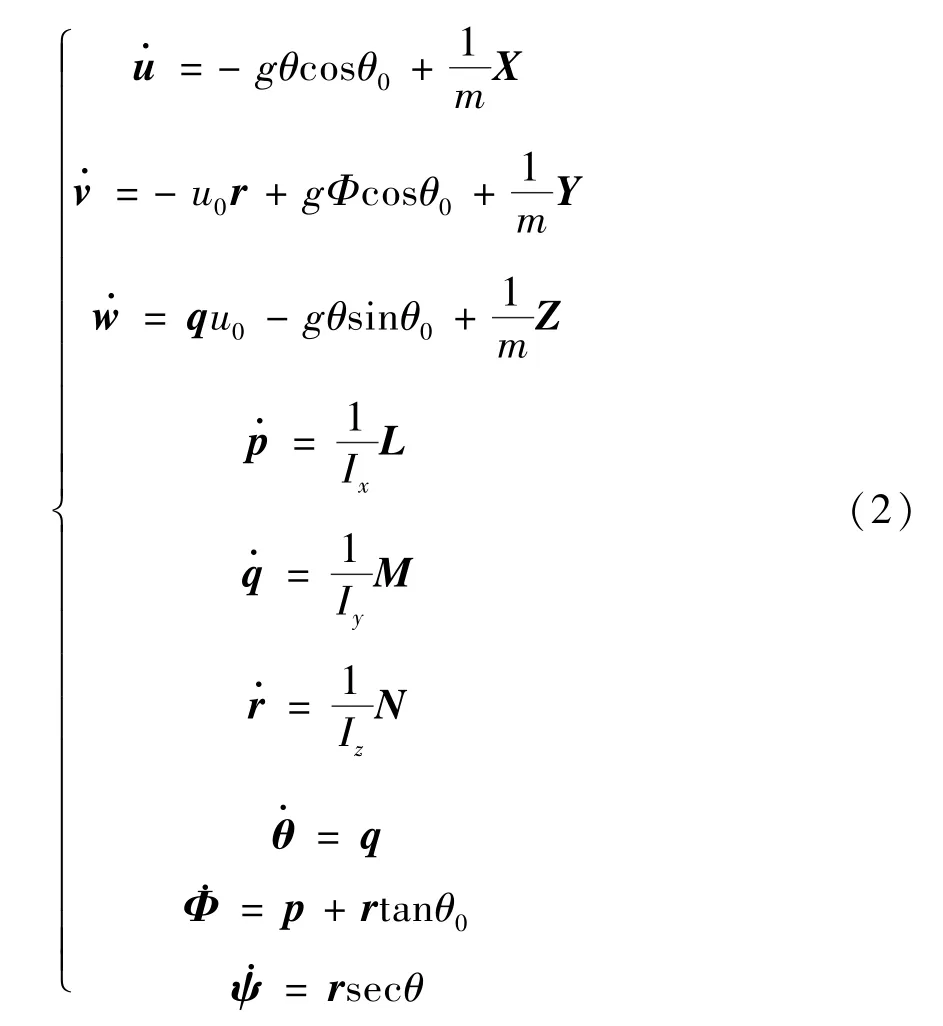
气动力与气动力矩的表达式如下,其中包含了系统产生的推力与力矩:
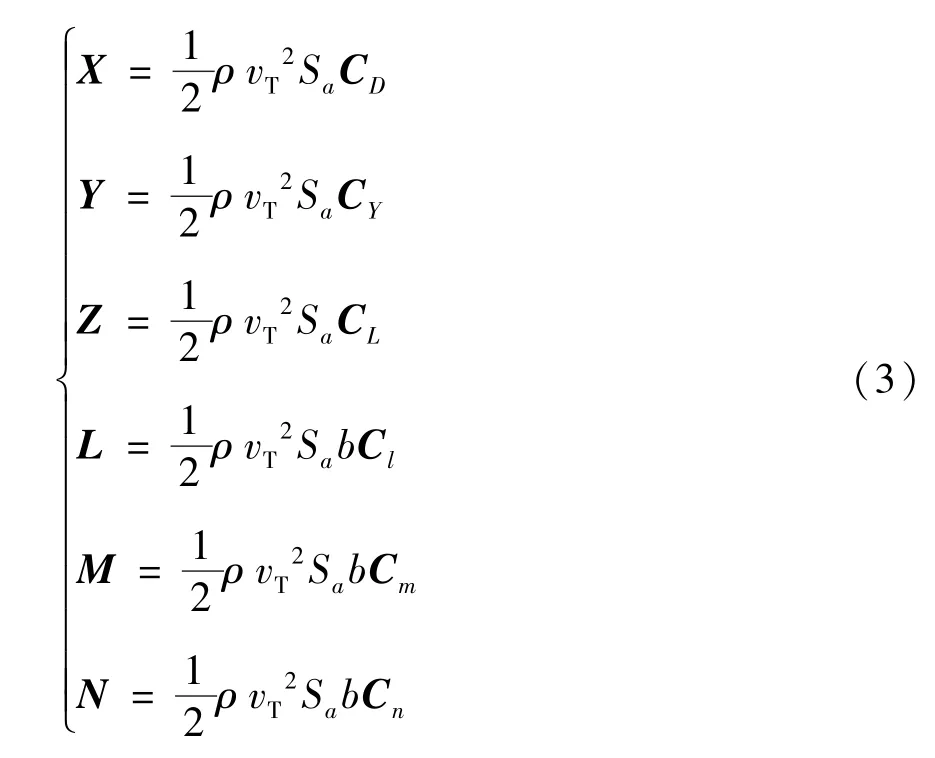
其中ρ为空气密度,θ0为俯仰角基准值,vT为基准速度(在小扰动线性化后即为u0),Sa为机翼面积,b为机翼长度,C(D,Y,L,l,n,m)为空气动力系数,通常由实验测得,其计算方式可参考文献[11]。
1.3 奇异摄动模型建立
为满足奇异摄动法进行快慢分解的要求,可将各变量表示为矩阵与行列式形式,其表示方法如式(4)所示。
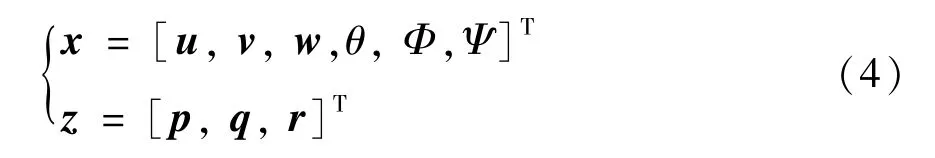
由式(2)可将固定翼动力学模型表示为


奇异摄动系统是带有小参数ε的系统,时标分解法在奇异摄动分解领域具有重要的作用。其原理为假设一个整体能够分解为快变化(非主导因素)和慢变化(主导因素)的系统。快子系统较于慢子系统的变化速率更快,达到稳定时所采用的时间也更少。引入小参数ε(0<ε <1),令z=εz1,可将式(5)表示为[12]

式(6)即为固定翼无人机的奇异摄动模型,其中F(x)=εF1(x),G=εB。
1.4 快慢子系统分解
奇异摄动方法能够根据不同的时间尺度,将系统分解为快子系统与慢子系统,对两个降阶子系统分别设计控制器以达到预期的控制目标。
显然可见常矩阵G为可逆矩阵,假设慢子系统的时间尺度为t,输入为u2s(t),则令ε=0,则由式(6)可求得降阶慢子系统:
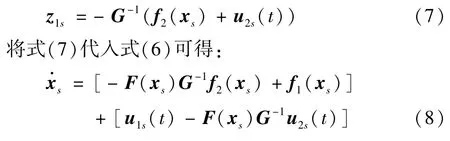
式(8)即为慢子系统数学模型。
由于z1=z1s +z1f,u2=u2s +u2f,在新的时间尺度下,能够近似认为慢变量保持不变,即,将式(7)代入下式:
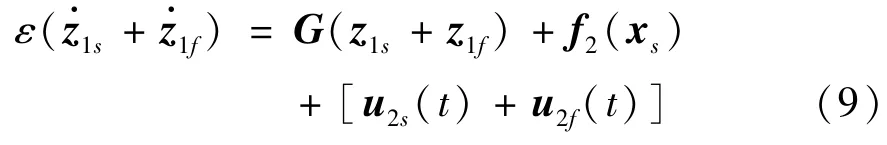
可求得快子系统的数学模型为

综上,式(8)、(10)构成了固定翼无人机的快慢子系统分解模型,其中x为线速度与姿态角向量,z为角速度向量。
2 优化PID 控制
2.1 传统PID 控制方法
传统的PID 控制方法所控制的对象通常为期望输出u0(t) 与实际输出y(t)的差值e(t),即:

传统PID 控制方法将e(t) 作为控制目标,通过比例(P)、积分(I)、微分(D) 3 个控制过程进行累加,从而得到控制量u(t),即:

然而,在固定翼模型使用传统PID 控制时,其对角速度等快变量的变化控制较为迟缓,调整时间过长,从而影响飞机舵机的调节能力,导致飞机稳定性变差。
2.2 基于奇异摄动的PID 优化控制
本设计采用奇异摄动时标分解方法,将固定翼无人机的系统飞行控制问题转化为不同的回路,分别设计控制器,此方法能够大大提高快系统回路的相应速度,同时提高各回路的控制精确性,其系统结构图如图2 所示。
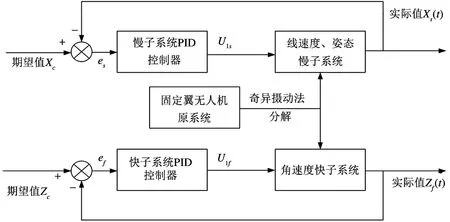
图2 基于奇异摄动的优化方法结构框图
首先,将原方程按照变化速率分解为快慢子系统,从而针对快子系统z(t)与慢子系统x(t)采用奇异摄动方法求得近似解xs(t) 与zf(t)。接着,根据求得的快慢系统近似解分别设计相应的PID 控制器,从而实现对无人机系统的优化控制。
针对式(8)所表示的慢子系统模型,设计对应的PID 控制量u1(t):
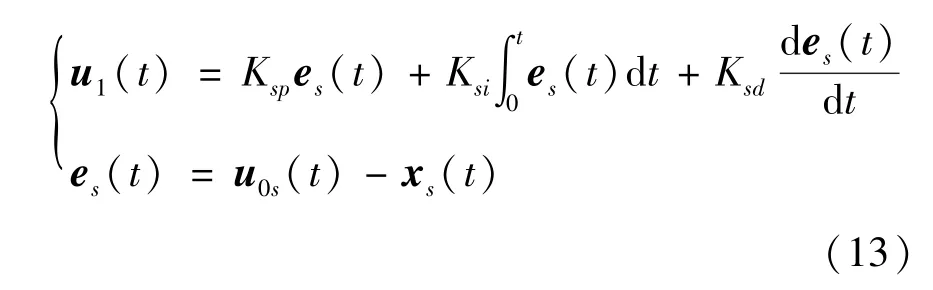
其中,Ksp、Ksi、Ksd分别为慢子系统的P(比例)I(积分)D(微分)系数,es(t) 为输出误差,us(t) 为系统控制量,u0s(t) 为慢系统输入期望值,xs(t) 为慢子系统输出。
同理,针对式(11)能够设计快子系统控制量:

对式(6)设计原系统PID 控制方法,其中:

即可求得固定翼无人机的奇异摄动控制优化PID 控制模型。
3 仿真与分析
由文献[11]可获得固定翼无人机的质量、翼展、面积等数据,再由其风洞实验可获得对应固定翼无人机的气动力参数等数据。
本文所做的仿真实验在Simulink 中运行,仿真目标是实现对机体坐标系下x轴的线速度和角速度进行控制,同时观测其在三维坐标系下的运动轨迹变化曲线。其中所涉及的参数及其数值如表3 所示。

表3 仿真相关参数
设置期望线速度为30 m/s,角速度为3 r/s,将参数代入式(7)可获得具体的快慢子系统,对快慢子系统分别做PID 控制器设计,在保证快慢子系统分别得到良好的控制情况下,获得的相应PID 参数为

整合快慢子系统控制方法,分别得到快慢系统以及原系统控制率为

将式(6)在Simulink 中进行仿真得到基于奇异摄动法的PID 优化模型(singularly perturbed PID control method,SP)并与传统PID 控制方法(traditional PID control method,TP)进行比较,得出的控制效果如图3 所示。
图3 为在固定翼无人机系统中加入TP 与SP 算法所得到的系统x轴线速度输出曲线。可以看到,采用SP 控制算法能够达到与TP 控制方法近乎相同的控制效果,都能够很快地达到稳态,并且其稳定时间与超调量都能够得到较为优异的控制。此验证说明对于慢子系统的优化控制,基于奇异摄动的优化方法能够达到与目前常用的PID 算法一样优异,对于角速度等快子系统的优化,其控制效果更优,如图4 所示。
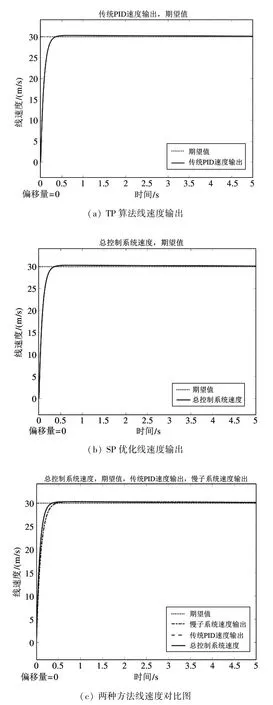
图3 两种算法线速度效果比较
图4(a)所示为TP 方法输出的x轴角速度曲线,图4(b)为SP 控制方法输出的角速度曲线,图4(c)为两种方法输出对比曲线。由图可得,对于快变系统的控制,传统PID 方法的跳变量较小,所需的调节时间过长,无法快速地达到期望值;这是由于奇异摄动法未忽略快子系统变化,而是单独考虑快子系统的控制方法而造成的。因此,经奇异摄动方法优化后的PID 控制能够在极短的时间内完成接近期望值的阶跃变化,同时能够极大地缩小调节时间,其对于角速度等快变量的控制效果要远高于传统PID。为验证SP 优化后的固定翼位置变化稳定性,本实验设置期望以x轴线速度30 m/s,z轴线速度10 m/s爬升5 s 后保持平飞。图5(a)为设定的仿真15 s 的固定翼速度变化轨迹,图5(b)为固定翼三轴位置变化轨迹。
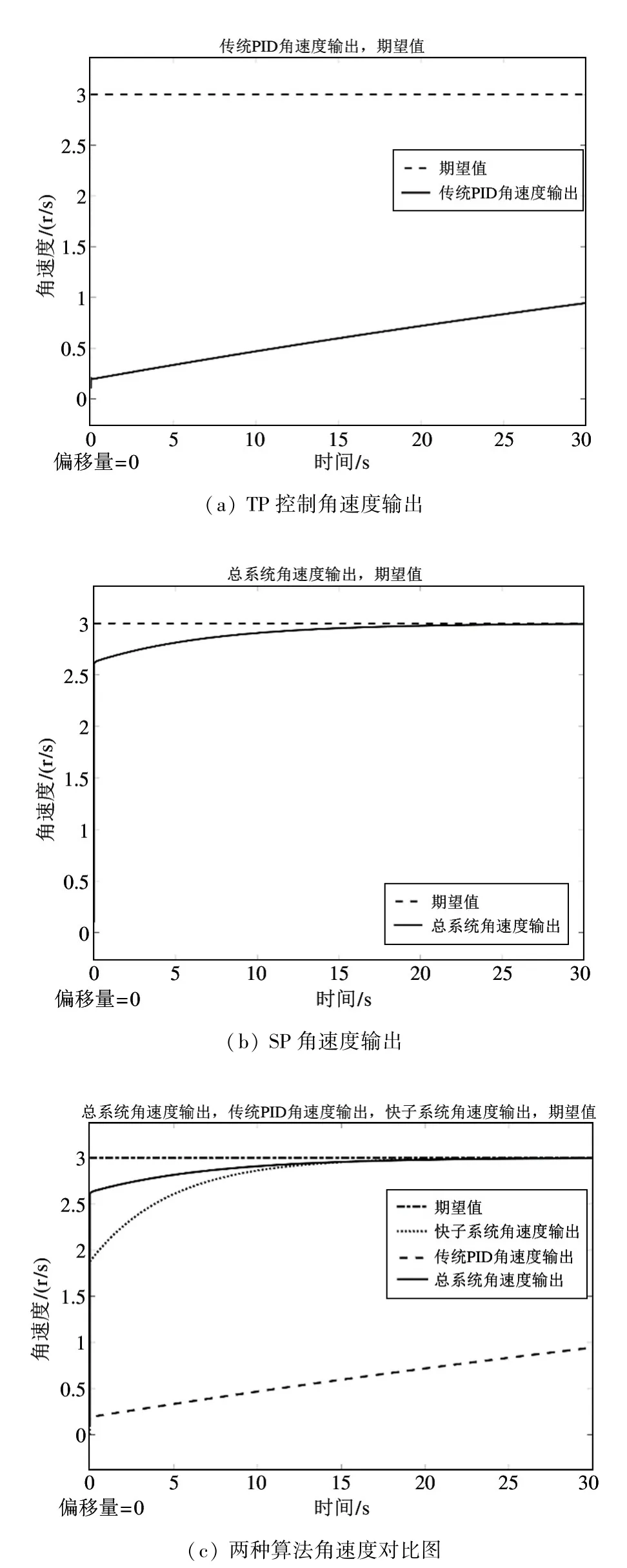
图4 两种算法角速度效果比较
由图5 可以看出,固定翼无人机在爬升阶段与平飞阶段能够保持较为平滑的线段,其飞行误差在运动中近似接近于0。此仿真表明本优化方法能够较好地控制固定翼无人机的飞行速度及姿态,对于位置控制也较为精确,相较于传统的固定翼控制方法,其理论有效性和先进性得到了证实。
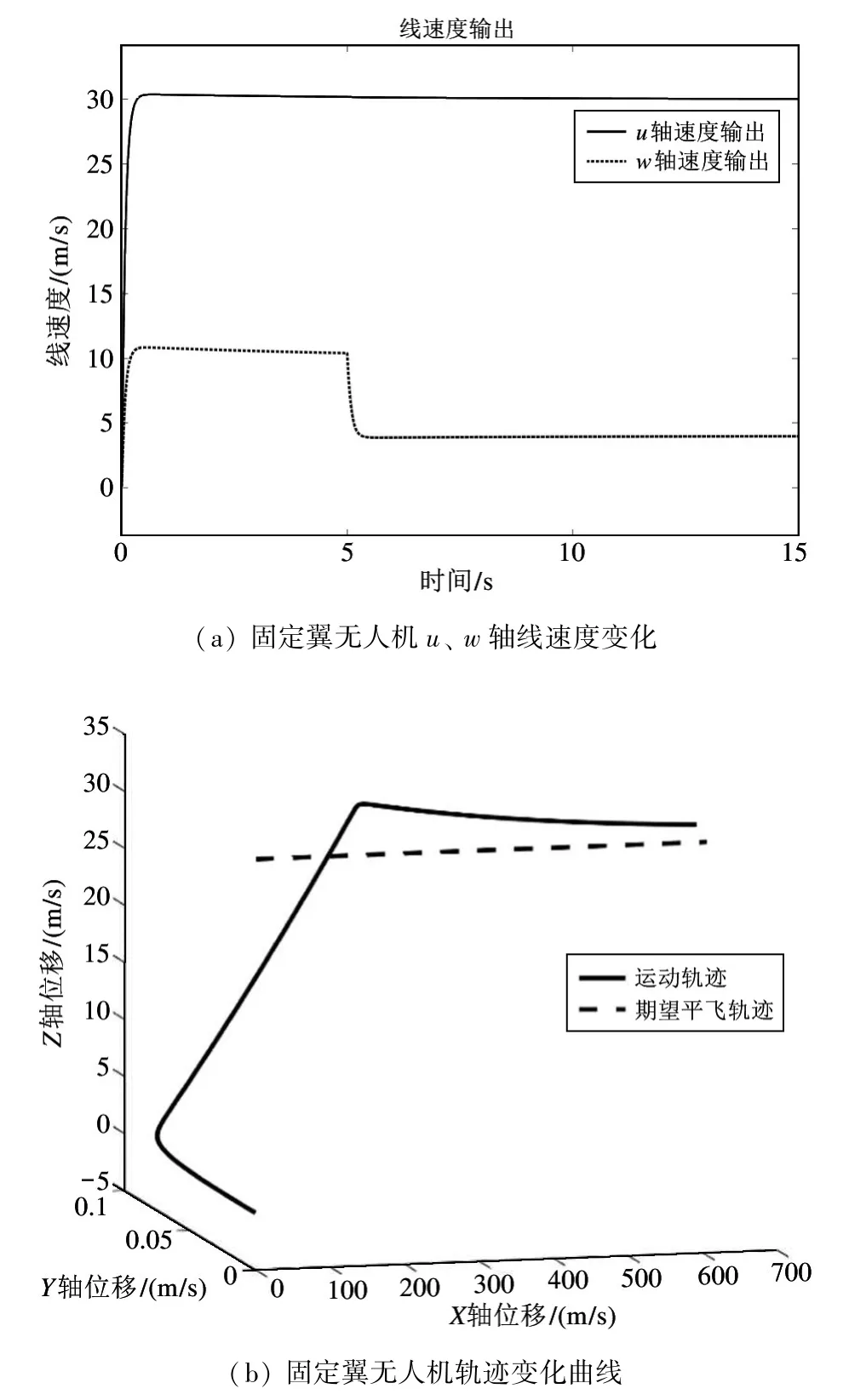
图5 固定翼速度及位置变化轨迹
4 结论
本文针对固定翼无人机进行了动力学建模,后采用奇异摄动法和PID 控制方法设计了固定翼无人机的奇异摄动优化PID 方法,并与传统PID 控制方法进行对比,实现了对固定翼无人机线速度与角速度输出的控制优化。仿真结果表明,对于线速度和角度等慢变量,奇异摄动优化PID 方法能够做到与传统PID 相同较为优异的控制效果;对于角速度等快变量,奇异摄动优化PID 方法能够达到更快的响应速度与更少的调节时间,其对于快变量的控制效果远远好于传统PID 控制方法。对于位置于姿态变化,本文方法能够进行有效的跟踪控制,同时减少控制时间,增加控制精度。

