基于定子磁场定向的永磁辅助同步磁阻电机无差拍直接转矩控制

翁子恺,储剑波

(南京航空航天大学 自动化学院，江苏 南京 211100)

0 引 言

永磁辅助同步磁阻电机(PMASynRM)具有调速范围宽、效率高、功率因数高、凸极比高等优点，在电动汽车、航空航天、家用电器等领域具有较好的应用前景[1-4]。与传统永磁同步电机(PMSM)相比，PMASynRM的电磁转矩由永磁转矩与磁阻转矩组成，占据主导部分的是磁阻转矩，其生产成本相对更低，发展前景较为广阔[5]。为了降低驱动系统的成本，提高驱动系统可靠性，在较多场合下均需要获取转子位置信息，因此无位置传感器方案也是PMASynRM研究的一个重点方向[6]。

与矢量控制策略相比，直接转矩控制(DTC)具有参数鲁棒性好、动态特性好、结构简单等优点，但也存在较大的转矩与磁链脉动。针对以上不足，国内外学者通过改进开关表、空间矢量调制技术、无差拍控制等对DTC进行优化。

文献[7]提出了一种基于复合转矩调节器的DTC策略，该策略设计了两个可变滞环，消除了转矩偏差和时间延迟对转矩脉动的影响，以优化DTC的转矩跟踪性能。文献[8]提出了适应低转速的DTC策略，引入转矩角的变化率作为速度估计的补偿，在无位置传感器的状态下更好地获取转速，有效抑制了转矩脉动。文献[9]提出了一种相位自整定定子磁链观测器，增强定子磁通观测器的鲁棒性和准确性，能够抑制转矩和定子磁链脉动。但基于开关表的DTC始终存在开关频率不固定及转矩、磁链波动明显的缺点。

文献[10]提出了一种基于M-T坐标系的SVM-DTC策略，将转速和转矩的PI控制器转化为转矩和磁链的PI控制器，降低了转矩和定子磁链脉动。文献[11]提出了一种定子磁链自适应的SVM-DTC策略，降低电机三相电流的输出，保持较低的转矩脉动，提高系统的功率因数，具有良好的稳态和动态性能。文献[12]提出了一种基于观测器的最优SVM-DTC策略，在静止参考系中采用最优控制理论来同时控制速度、转矩和磁链变量，该方法具有计算量小、转矩和磁链脉动小、鲁棒性强、瞬态响应好等优点。但由于PI控制器的引入，导致转矩的动态性能受PI参数的影响较大。

文献[13]提出了一种基于有效磁链观测器的无差拍直接转矩磁链控制(DB-DTFC)方法，实现了电机的无速度传感器控制，但其计算方法较为复杂，且受参数影响较大。文献[14]提出了一种基于静止坐标系的DB-DTC策略，但仅适用于隐极性PMSM。文献[15]提出了一种简化的DB-DTC策略，将电压的计算与磁链分离，该策略不受永磁磁链估计误差的影响，减少了算法的计算时间和复杂性，但可进行进一步的简化。文献[16]提出了一种基于定子磁场定向的DB-DTFC策略，将电压的计算与磁链分离，实现了对电磁转矩和定子磁链的解耦，减小电磁转矩和定子电流的脉动，并使动态响应、计算量以及鲁棒性等方面的性能均得到了改善，但是需要进行坐标变换。

为降低直接转矩控制的转矩脉动，提出了一种改进型DB-DTFC算法。基于有效磁链估算转子角度，并基于电机的数学模型推导DB-DTFC的公式，说明其能应用于PMASynRM。在x-y坐标系上建立电压分量与定子磁链和转矩的关系，实现基于定子磁场定向的DB-DTFC，降低了DB-DTC算法的复杂度。通过仿真证明本文提出控制策略的有效性。

1 PMASynRM的基本方程与有效磁链

图1为PMASynRM的结构示意图。与同步磁阻电机相比，PMASynRM转子中加入的铁氧体永磁材料只起到辅助励磁的作用。

图1 PMASynRM结构示意图

1.1 电机数学模型

为了便于简化分析，对PMASynRM做出如下假设：忽略铁心饱和问题，不考虑铁心涡流和磁滞损耗；永磁材料的导电性为零；磁场在气隙中呈正弦分布。

当PMASynRM稳态运行时，其转子坐标系下的电压方程为

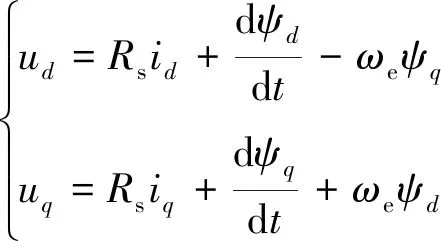
(1)

其中：

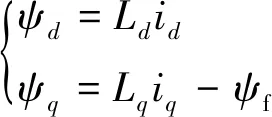
(2)

式中：ud、uq，id、iq，ψd、ψq分别为定子电压us、定子电流is和定子磁链ψs在d、q轴上的投影；Rs为定子电阻；ωe为转子电角速度；Ld、Lq分别为d、q轴电感；ψf为电机永磁磁链。

电磁转矩方程为

(3)

式中：p为电机的极对数。

电磁转矩Te同样可以用定子磁链幅值和转矩角δ表示为

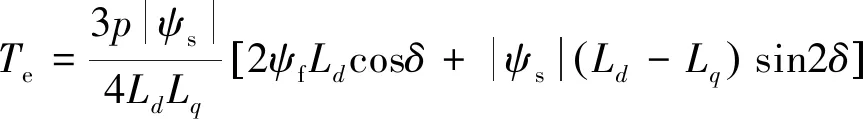
(4)

1.2 PMASynRM的有效磁链

对于PMASynRM，定义有效磁链ψa与q轴方向一致,其公式为

ψa=(Lq-Ld)iq-ψf

(5)

将式(5)代入电机磁链方程式(2)中：

(6)

将式(6)经过坐标转换，可得αβ坐标系下的有效磁链：

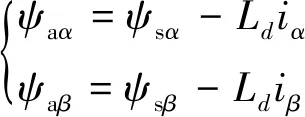
(7)

式中：ψsα、ψsβ，ψaα、ψaβ，iα、iβ分别为定子磁链、有效磁链以及定子电流在αβ坐标系下的分量。

定子磁链经过式(7)的计算后，根据有效磁链提取的估计角度值为

(8)

这一角度即α轴与永磁磁链的夹角，计算得到的角度值和传统定义的电角度值θr相差90°，因此有：

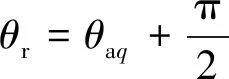
(9)

为了降低参考定子电压的计算复杂性和难度，定义基于定子磁链定向的两相旋转坐标系，新坐标系的x轴位于定子磁链矢量上，y轴与x轴垂直，如图2所示。αβ坐标系中变量可通过定子磁链角θs变换到xy坐标系中，电流矢量变换如下所示：

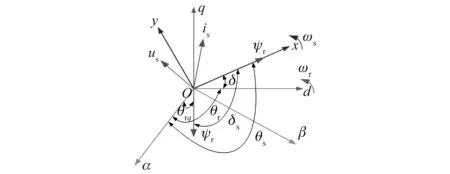
图2 定子磁链矢量分布图

(10)

式中:ix、iy为定子电流在xy坐标系下的分量。

2 PMASynRM的DB-DTC及其优化

传统DB-DTC应用于PMASynRM的计算繁琐，公式推导复杂，因此设计了改进型DB-DTC算法，以优化控制性能。

2.1 传统DB-DTC在PMASynRM的理论分析

将式(1)所示电机的电压方程移项并代入磁链方程式(2)，并对其进行整理和离散化：

(11)

其中：

X=ψd(k)+ωrTsψq(k)-Rsid(k)Ts=

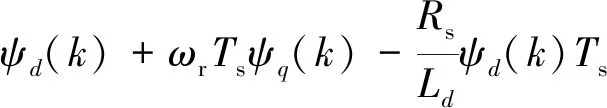
(12)

Y=ψq(k)-ωrTsψd(k)-Rsiq(k)Ts=

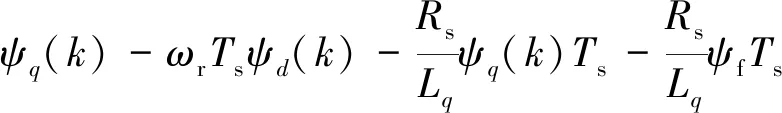
(13)

将式(2)代入转矩方程式(3)中求导并离散化得：

(14)

式中:Ts为采样周期;k为当前采样时刻；d轴磁链变化量Δψd=ψd(k+1)-ψd(k)；q轴磁链变化量Δψq=ψq(k+1)-ψq(k)。

转矩误差可写成ΔTe=Te(k+1)-Te(k),整理后得：

uq(k)Ts=Mud(k)Ts+B

(15)

其中：

(16)

(17)

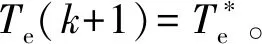
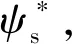
[ψs(k+1)]2=[ψd(k+1)]2+[ψq(k+1)]2=

(18)

最终解一元二次方程得到：

(19)

(20)

其中:

式(19)与式(20)即为DB-DTFC控制律,根据观测k时刻电机的定子磁链、电磁转矩、转速及所需的其他电机参数,可以分别计算出k时刻应施加在定子端的电压ud(k)、uq(k)。ud(k)、uq(k)经过旋转坐标逆变换即可得到两相静止坐标系下的目标电压uα(k)、uβ(k)。

2.2 基于定子磁场定向的DB-DTFC

传统DB-DTFC是根据dq轴的磁链与转矩方程进行推导，而对基于xy坐标系的磁链与转矩方程进行推导可降低参考定子电压的计算复杂性。

xy坐标系中的定子电压可表示为

(21)

定子磁链矢量位于x轴上，因此：

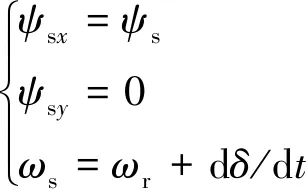
(22)

把式(22)代入式(21)中，xy坐标系下的定子电压可进一步推导为

(23)

式中：usx(k)、usy(k)、isx(k)、isy(k)为第k时刻的xy坐标系下的定子电压与电流，ψs(k+1)、δ(k+1)为第k+1时刻的定子磁链幅值和转矩角。

根据式(4)，对电磁转矩求导并离散化得：

(24)

电磁转矩和转矩角之间的关系可以进一步推导为

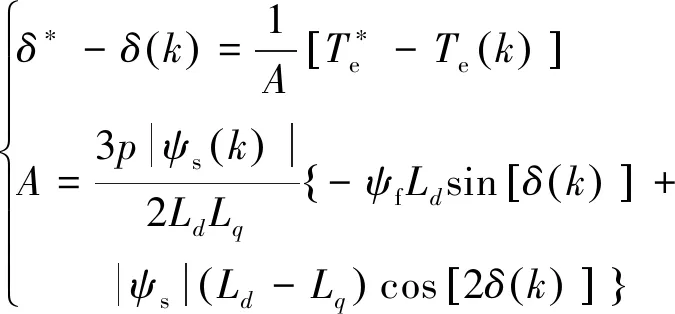
(25)

根据无差拍原理，把参考定子磁链幅值和转矩角赋给第k+1时刻的定子磁链幅值和转矩角，并结合式(23)与式(25)，参考定子电压可表示为

(26)

由此可见，x轴的电压分量只与定子磁链的幅值有关，与转矩的幅值无关；y轴的电压分量只与转矩的幅值有关，与定子磁链的幅值无关，从而对定子磁链与电磁转矩进行解耦。采用式(10)的逆变换矩阵，将式(26)变换到αβ轴上的参考定子电压。

但是，以上计算公式仅适用于磁链恒定时，在需要改变磁链大小的情况下转矩对时间微分并离散化得：

(27)

令转矩角变化量为Δδ=δ*-δ(k)。此时有：

(28)

其中：

(29)

(30)

此外，该方法能够对静止坐标系中SVM-DTC的表示方法进行推导。在SVM-DTC中，下一时刻的电压给定由给定磁链幅值和定子磁链角共同计算得到：

(31)

因此，在静止坐标系中根据无差拍原理求取下一时刻的定子磁链角即可实现无差拍控制，如下式所示：

(32)

式(32)中Δδ可通过式(25)或式(28)中的转矩角变化量求得。与2.1节中的DB-DTC方案相比，该方案无需进行坐标变换，无需求解一元二次方程，简化了计算。与SVM-DTC相比，该方案的定子磁链角给定值根据无差拍原理获取而非PI环的输出，同时由于其结构的相似性，对DB-DTFC和SVM-DTC进行仿真对比。

3 仿真验证与结果分析

根据PMASynRM的dq轴电压、电流等公式，在MATLAB/Simulink工具中搭建电机数学模型。基于磁链转矩方程、无差拍等搭建电机的DB-DTFC系统，如图3所示。DB-DTFC系统包括磁链转矩计算模块、SVPWM模块、无差拍模块等若干子系统模块。

图3 基于DB-DTFC的PMASynRM控制框图

电机仿真参数如表1所示。

表1 PMASynRM电机参数表

采用PMASynRM DTC，仿真条件为，电机给定转速n*=12 000 r/min，给定形式为斜坡函数，斜率为3 000 r/(min·s)；直流侧电压Udc=311 V；负载转矩初始给定TL=0.1 N·m；仿真时长为10 s，在t=0.2 s时系统切换成DB-DTFC算法，将磁链转矩观测器估算的电机转速和角度信息反馈至转速环和无差拍计算模块。

图4～图6是12 000 r/min转速下SVM-DTC和改进型DB-DTFC系统的波形对比图。

图4 电机转速波形

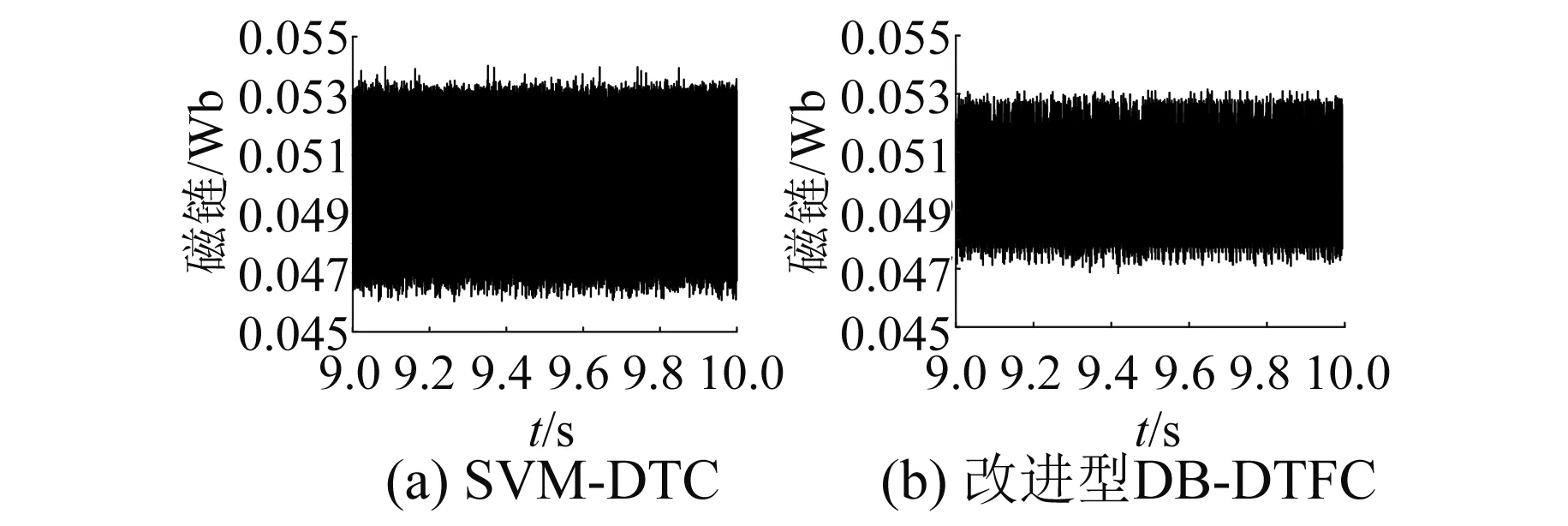
图5 电机磁链波形

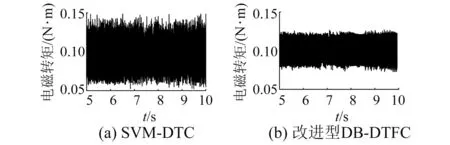
图6 电磁转矩波形

由图4的波形对比可知，SVM-DTC控制方案的电机转速存在50 r/min左右的超调，且转速振荡较大，动稳态性能一般；采用改进型DB-DTFC则转速波动较小，无明显超调，动稳态性能优秀。

对比图5波形，SVM-DTC的定子磁链脉动为7.6%。改进型DB-DTFC的定子磁链脉动为5.8%。证明改进型DB-DTFC能较为有效地减小磁链波动。

对比图6波形可知，SVM-DTC的转矩脉动为±0.045 N·m，改进型DB-DFTC的转矩脉动为±0.025 N·m，改进型DB-DFTC的转矩脉动比SVM-DTC大幅度减小。

对仿真系统做给定转速突增突减测试。在t=6 s时分别对给定转速突增和突减1 000 r/min，其余仿真条件如上。

由图7～图10波形可知，在对电机突增或突减给定转速时，SVM-DTC的速度向上和向下阶跃的响应时间分别为0.21 s和0.14 s；改进型DB-DTFC策略的速度向上和向下阶跃的响应时间分别为0.14 s和0.10 s。改进型DB-DTFC策略的转矩和速度动态响应时间快于SVM-DTC策略，有良好的动态性能。

图7 给定转速突增1 000 r/min时电机转速波形

图8 给定转速突增1 000 r/min时电机转矩波形

图9 给定转速突减1 000 r/min时电机转速波形

图10 给定转速突减1 000 r/min时电机转矩波形

对仿真系统做负载阶跃测试。在给定转速600 r/min下t=0.3 s时分别令负载转矩TL由0增加至2 N·m及由2 N·m减小至0。

由图11和图12波形的对比可知，当负载转矩突增时，SVM-DTC和改进型DB-DTFC电磁转矩值分别经过0.003 s和0.002 s调节至新的负载电磁转矩值，当负载转矩突减时分别经过0.002 5 s和0.001 7 s调节至新的负载电磁转矩值。改进型DB-DTFC能有效地抑制转矩脉动且转矩动态响应性能优于SVM-DTC。

图11 突加2 N·m负载转矩时电机转矩波形

图12 突减2 N·m负载转矩时电机转矩波形

4 结 语

为提高PMASynRM DTC的动稳态性能，设计了一种改进型DB-DTFC算法。该算法基于定子磁场定向的坐标系上的电压分量实现了定子磁链和转矩的解耦控制，并将其应用于静止坐标系中。仿真与分析结果表明，改进型DB-DTFC算法相比于SVM-DTC算法，拥有较好的稳态、动态性能，能够有效地抑制转矩脉动。