基于FLUENT 的竖井旋流泄洪洞水力特性模拟分析
高梦露
(1.福建省水利水电勘测设计研究院有限公司,福建 福州 350001;2.福建省水动力与水工程重点实验室,福建 福州 350001)
1 引言
旋流竖井具有适应流量范围大、水力现象稳定、洞线灵活和高消能率等优势,近年来被广泛应用于城市防山洪排涝、导流洞改建、高速水流泄水等工程中[1-2]。关于采用数值模拟的方法研究旋流竖井的水力特性,程庆迎[3]对水平旋流竖井的流动特性进行了详细模拟。杨海波等[4]对竖井的泄流能力和消能率以及洞顶余幅进行了验证。栗帅等[5]对竖井高尾水位条件下排气、流态和压强等分布进行了模拟。何军龄等[6]选取不同的紊流模型对超高水头、大流量强旋转的竖井进行了模拟以及对比分析。高志芹[7]对甲岩水电站旋流竖井从水力计算、物数模耦合、结构等方面论述了竖井旋流泄洪洞的设计研究。关于研究脉动压力的特性,秦亮等[8]对产生水跃现象的底板进行模拟。王旭[9]对泄水建筑物坝面隔墙脉动压力分布规律进行了模拟。此外,还有诸多学者探讨旋流竖井数值模拟方法。
因此,本文拟建立某工程竖井旋流泄洪洞三维整体数学水力学模型,旨在根据项目特点,研究其水力特性,验证竖井结构的可行性,为隧洞安全运营提供参考。
2 研究区概况
某小(2)型水库,工程等别Ⅴ等,水库洪水标准按20 年一遇设计,200 年一遇校核。水库大坝为混凝土面板堆石坝,最大坝高22.50 m,坝顶长度76.0 m。溢洪道为岸边侧槽式,位于大坝左岸,进口为宽顶堰,无闸控制,堰顶高程82.48 m,堰顶宽度19.00 m,下泄流量36.15 m3/s。现因修建地铁,隧道及高架桥部分占用溢洪道,影响水库汛期泄洪。故计划改造为旋流竖井的泄洪方式,改造示意图见图1。
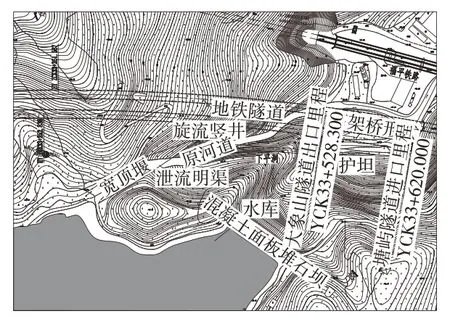
图1 溢洪道改造示意图
旋流竖井从上游至下游主要水工建筑物依次由宽顶堰、泄流明渠、涡室、竖向导流坎、竖井、涡室与竖井衔接的圆锥过渡段、水垫塘、泄洪洞、压坡段及护坦组成,护坦出口接原河道。泄流明渠长70.34 m,宽19 m~1.89 m,坡降0.337,左边墙1/4 椭圆曲线与涡室偏心连接。涡室底高程60.00 m,收缩段底高程54.00 m,水垫塘底高程17.08 m,明流泄洪洞进口底高程20.72 m,坡降0.005。采用2.5 m×3.0 m 城门洞型断面。为防止流速过大、涡室内壅水过高,且保证旋流稳定,在涡室内加设竖向导流坎避免竖井内水流与来流冲撞。为稳定泄洪洞内的水流及配合下游护坦处消能设计,泄洪洞进口加设1∶6 的压坡段,长10.8 m,出口3.0 m×1.2 m 矩形断面。
项目最大特点是小流量大流速,存在的问题:(1)考虑到涡室进口流速较大,避免水流在涡室内壅水过高,涡室内径需较大;(2)考虑到来流量较小,避免造成工程量浪费,涡室内径又需较小。经过多组次试验得出竖井内径为2.8 m,涡室内径为6.4 m,为竖井内径的2.28 倍,与传统的1.2 倍~1.6倍不同,整体形似头大身小的“漏斗”,竖井可能导致出现涡室内壅水、竖井内呛水等现象,有必要对其水力特性展开研究。
3 数学模型、边界及测点采集
3.1 数学模型
3.1.1Realizable k-ε 紊流模型
对除去脉动特性的研究采用Reynolds 平均法中的Realizable k-ε 模型,能够更有效地模拟旋转均匀剪切流、包含有射流和混合流的自由流动、管道内流动、边界层流动以及带有分离的流动等不同类型的流动[10]。水流控制方程包括连续性方程、动量方程、紊动能方程和紊动能耗散率方程。
连续方程:

动量方程:
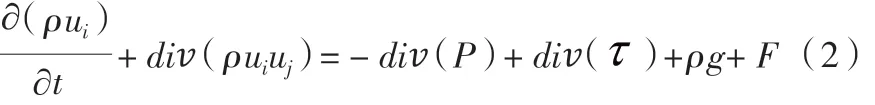
湍动能k方程:

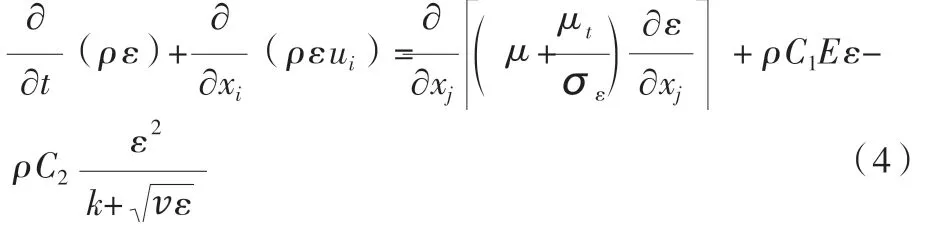
式中:t为紊流粘性系数, 和σε分别为k和ε的紊流普朗特数,σk=1.0 , σε=1.2;C1和C2为模型常数,为由平均速度梯度引起的湍动能k的产生项,
3.1.2大涡模拟
对脉动特性的研究采用计算瞬时量的大涡模拟(LES),首先建立一种数学滤波函数,放弃全尺度范围上的涡的瞬时运动的模拟,将尺度比滤波函数的尺度小的涡滤掉,从而分解出描写大涡流场的运动方程,而这时被滤掉的小涡对大涡运动的影响,则通过一定的模型在针对大涡流场的运动方程中来体现[10]。
通过滤波函数处理瞬时状态下的Navier-Stokes 方程及连续方程,有:

以上两式控制方程组完全是瞬时状态下的方程。τij=体现了小尺度涡的运动对所求解的方程的影响。
3.1.3VOF 模型
选取VOF 模型追踪模拟自由表面运动,控制方程为:

式中:aw为水的体积分数。
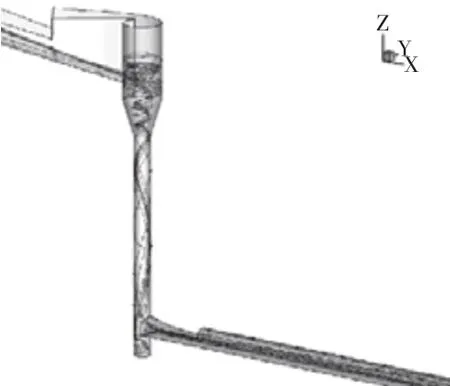
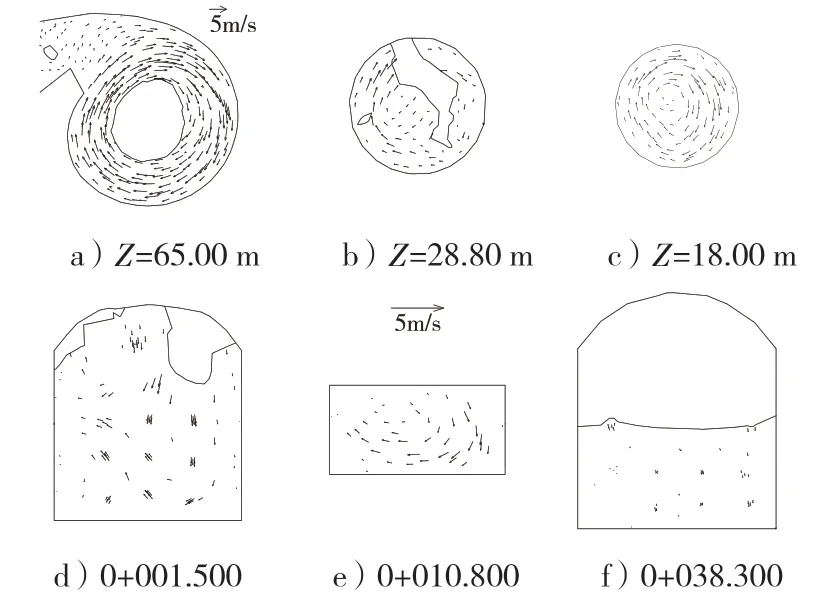
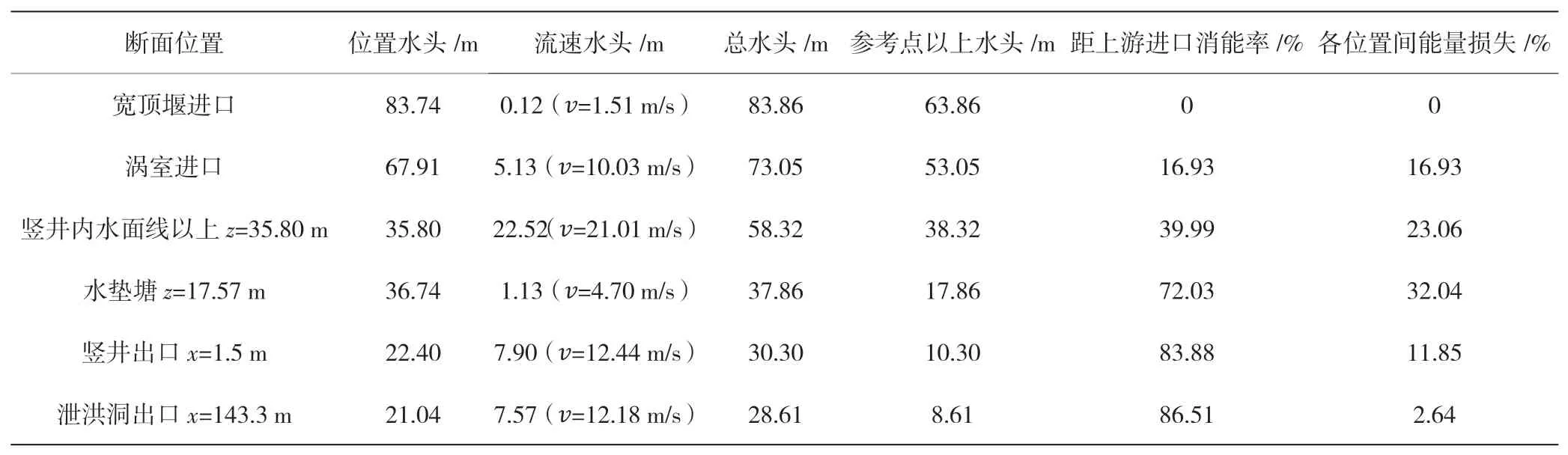
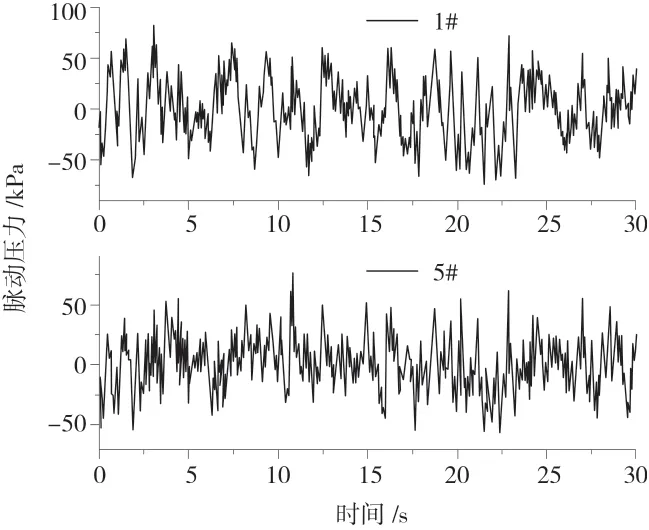
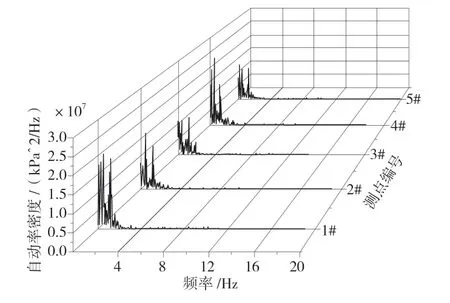
本文中研究竖井内水气二相流运动,流体的容积分数总和为1。aw= 0 表示控制体积内不存在水;aw= 1 表示控制体积内只存在水;0 建立从泄流明渠至泄洪洞的整体三维数值模拟计算区域。其中泄洪洞建立于X 轴方向,高程建立于Z 轴方向,以竖井中心线位置为桩号0+000.000,则即计算区域范围从桩号泄流明渠进口桩号0-082.000 至泄洪洞出口桩号0+143.300。竖井体型复杂,宜采用适应性好的四面体单元的非结构化网格。模型网格尺度0.3 m~2.0 m,网格数量40 万,网格节点7 万。 采用有限体积法显式迭代求解,速度压力耦合采用适合水气二相流的PISO。上边界为明渠流进口,设置为流速进口边界;下边界为泄洪洞自由出流,设置为压力出口边界;泄流明渠为明流,与空气接触的边界设置为压力进口边界;在固壁上给定法向的速度为零和无滑移条件,近壁的黏性底层采用标准壁面函数处理。初始流场根据实际情况设置计算水位以下竖井内全部充满水,以上全部充满气。该方法曾多次用于有压和无压旋流竖井的研究,物数模吻合良好。 水垫塘底部脉动压力测点分布见图2,5#为底部中心,1#~4#分别距中心1 m,且1#和3#平行于泄洪洞纵轴线,2#和4#垂直泄洪洞纵轴线。根据那奎斯特采样定理,采样频率必须大于脉动频率的两倍,才能保证频域不会失真,已有的分析结论及工程经验显示水流脉动压力主要频率一般不超过20 Hz,因此脉动压力采样频率取125 Hz,即每个测点采集间隔 0.008 s,采集次数3840 次,采集时间30.72 s。 图2 网格示意及脉压测点布置 图3可知水流沿着椭圆边墙收缩方向进入涡室后做离心运动,呈顺时针旋流而下,形成稳定的掺气空腔。由于涡室进口过水断面逐渐束窄,加之涡室内的部分旋转水流与来流碰撞引起来流受阻,故涡室进口处发生水跃,起跃位置至涡室进口长约11.60 m,水跃长度较短,且弗氏数约2.78,属急流,不会影响涡室进水口的泄流能力。 图3 整体流线分布 图4可知涡室内最大壅水高程68.20 m。空腔区约在锥形过渡段54.60 m 高程处空腔最小,直径约1.30 m,不会因竖井内径相比涡室较小而发生呛水现象。随着竖井内越往下垂向流速越大,水层厚度越薄,对应空腔半径越大。空腔底高程约Z=34.60 m,由于底部的水垫塘近乎满流,形成水垫,竖井内产生环状水跃,水跃范围约Z=34.60 m~20.10 m。泄洪洞进口水流由顺时针旋流突变为水平流,流态紊乱,通过采用压坡的方式,水面波动逐渐趋于平缓,气体析出。泄洪洞内最大水深在桩号0+012.210 处,为1.33 m,未超过直墙范围,洞顶余幅0.52,净空高1.67 m,满足要求。 图4 断面流态 图5反映了水流沿着壁面旋转,在中央形成稳定的空腔,直至(g)Z=34.60 m,产生环状水跃后水流运动紊乱。进入水垫塘Z=20.10 m 后,流速降低,水垫塘呈满流状态。 图5 竖井横剖面流态分布 图6可知,竖井沿程无负压分布,在涡室段至锥型过渡段压强为1.39 m~10.45 m,沿竖井向下至环状水跃附近,流速越大,压强越小,逐步降低至0.22 m,环状水跃以下遇水垫塘,压强迅速增大,压坡段全程正压,保证了压坡效果。水垫塘底部受水流冲击,是压强最大区域,最大压强24.00 m,最小18.49 m,平均20.58 m。图7(a)~(c)可知,同一高程的竖井断面,壁面压强最大,沿径向递减。图7(d)~(f)可知,竖井经过压坡进入泄洪洞压强稳定。 图6 竖井压强分布 图7 沿程断面压力分布 涡室进口处平均流速约10.03 m/s,在竖井段高程约35.80 m的处增至约21.01 m/s,水流空化数0.46,大于初生空化数0.3,未出现空蚀空化问题。水垫塘内平均流速约5.28 m/s,经泄洪洞压坡段后平均流速约12.18 m/s。图8(a)~(c)可知,竖井内水流沿壁面旋流而下,环状水跃范围内流场分布紊乱,水垫塘内流速较小。经过压坡段后流速稳定,如图8(f)桩号0+038.300 流速场分布平稳。 图8 沿程断面流速矢量图 以泄洪洞出口高程20.00 m 为参考点,选取6 个剖面位置分析各段的消能率,见表1。从库上游进口至涡室进口,即泄流明渠段由于坡度较陡、末段水跃,消能率为16.93%。而涡室进口至竖井水面线以上能量损失23.06%,原因是水流贴壁旋流路程增加,沿程阻力增大。水垫塘内消能率为72.03%,能量损失最多,为32.04%,原因是水流在竖井内产生环状水跃以及水垫塘消能,与壁面摩擦、水气混掺剪切作用下消耗能量。可见竖井的主要消能场所是环状水跃产生位置和水垫塘。总消能率为86.51%,若不设压坡,计算得出竖井总消能率90%,与卫勇[11]和何军龄[12]研究成果描述一致,压坡虽然能稳流,但会导致竖井内自由水面(环状水跃)位置升高,总消能率降低。但总体来看,消能效果良好。 表1 消能率计算表 水垫塘底板受水流冲击,底板脉动标准值最大[13]。均方根能够表示紊动程度的强弱,也称脉动强度[14]。压力脉动均方根表示为: pi和p分别为瞬时压力和时均压力。脉动压力概率密度分布中偏态系数Cs和峰态系数CE能够表示脉动压力序列分布与标准正态分布的偏离程度。标准正态分布,Cs= 0、CE= 3。自功率谱密度函数能够表示脉动压力的功率在频域内随频率的分布[15-18]。 1#~5#测点统计特征值见表2,脉动压力均方根为20.25 kPa~28.12 kPa,1#和5#测点脉动压力时程分布见图9,各测点时程图与其相似。根据前学者相关书籍及文献表明,此底板脉动压力值属正常范围。脉动压力概率密度分布是否符合正态分布采用序列的偏态系数Cs和峰态系数CE来验证,Cs>0 则为高于时均值的脉动压力出现的概率较高,CE>3 则为脉动压力分布较为集中,反之亦然[19-20]。Cs值为-0.38~0.08,CE值为2.45~3.62,脉动压力呈正态分布,1#和5#测点脉动压力概率密度分布见图10,其他类似。水垫塘底板脉动压力通过快速傅里叶变换,脉动压力频域内随频率分布用自功率谱密度函数表示,见图11。各测点优势频率为0~4 Hz,主频为0~1.27 Hz,水流脉动压力的优势频率集中于低频范围,不会引起竖井的共振危害。 图9 测点脉动压力时程线图 图10 脉动压力概率密度分布 图11 测点自功率谱密度函数 表2 测点统计特征值 (1)本项目最大的特点是小流量大流速,整体形似头大身小的“漏斗”。从水力学角度,旋流竖井流态稳定,竖井内形成稳定空腔,未因竖井内径相比涡室较小而发生呛水现象;沿程未出现负压,水垫塘底部受水流冲击,是压强最大区域,最大压强24.00 m,最小18.49 m,平均20.58 m;竖井内最大流速约21.01 m/s,水流空化数0.46,大于初生空化数0.3,未出现空蚀空化问题;主要消能场所在水跃位置和水垫塘。从宽顶堰进口至泄洪洞出口总消能率为86.51%,若无压坡,计算得出竖井总消能率90%,可见压坡虽然能稳流,但会导致竖井内自由水面(环状水跃)位置升高,总消能率降低。但总体来看,消能效果良好。 (2)水垫塘底板各测点脉动压力均方根为20.25 kPa~28.12 kPa,呈正态分布,优势频率为0~4 Hz,主频为0~1.27 Hz,水流脉动压力的优势频率集中于低频范围,不会引起竖井的共振危害。3.2 计算区域和边界条件
3.3 脉压测点布置与采集

4 计算结果分析
4.1 流态分布
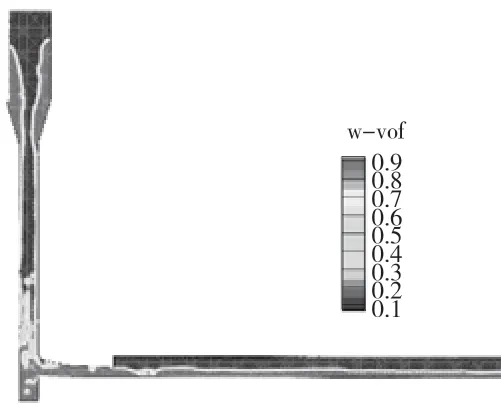

4.2 压强分布


4.3 流速分布
4.4 消能率
4.5 脉动压力
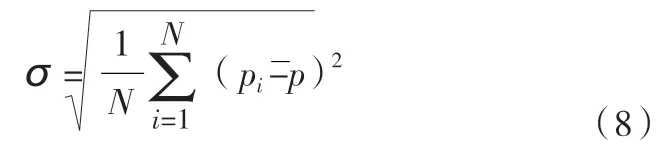


5 结论

