计及不确定性的智能机器人钻锚机械臂运动学误差分析

俞利宾，杨碧涛，吴 昊

(1.红河学院 工学院,蒙自 661199；2.云南省高校高原机械性能分析与优化重点实验室，蒙自 661199）

0 引言

对于智能机器人钻锚机械臂而言，末端执行器元件与主关节结构之间的运动关联度能够描述机械臂的运动误差行为，运动关联度指标的物理数值越大，机械臂运动误差行为的表现能力也就相对较为薄弱。在一些动作单一的应用场合中，机械臂只要能够准确到达各标记节点，就能够满足智能机器人的实际运动需求。随着科学技术手段的不断进步，机械臂的应用范围也在逐渐扩大[1]。在此情况下，由于应用环境的日益复杂化，机械臂元件往往不能完全达到已标记的各个运动节点，这也是导致运动误差行为出现的主要原因。完整的智能机器人钻锚机械臂由主关节、末端执行器等多个元件共同组成，且受到非相关运动行为的影响，关节转动角数值也会出现一定程度的改变。此时，末端执行器元件与主关节结构之间的统一运动趋势被打破，进而引发了明显的机械臂运动误差行为。为解决上述问题，提出计及不确定性的智能机器人钻锚机械臂运动学误差分析方法。

1 智能机器人钻锚机械臂的运动学参数标定

为实现对智能机器人钻锚机械臂的运动学参数标定，在已知机械臂组成结构的基础上，建立运动学参数模型。

1.1 机械臂结构组成

智能机器人钻锚机械臂由旋转杆、连接器、启动器、帮锚结构、顶锚结构等多个元件共同组成，其具体连接形式如图1所示。

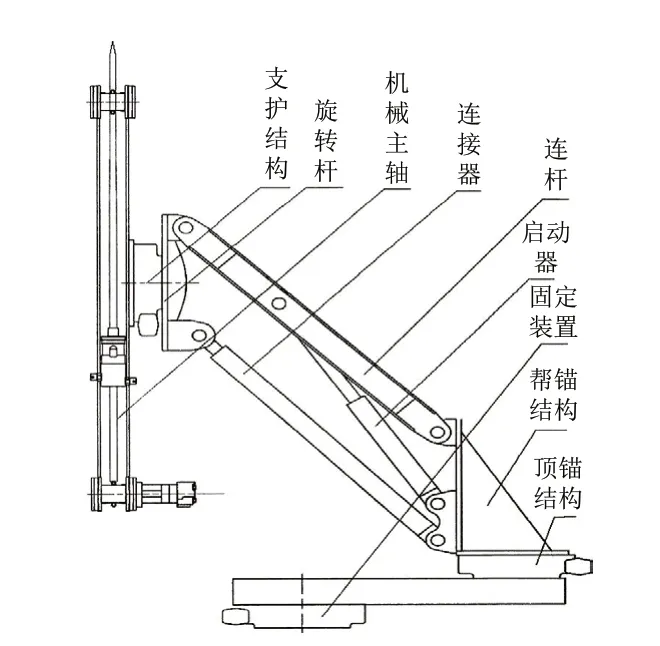
图1 智能机器人钻锚机械臂组成结构

支护结构、旋转杆、机械主轴作为机械臂元件的主臂体成分，整体呈现出竖直存在状态。其中，机械主轴位于主臂体中间，可在旋转杆元件的作用下，将其所承担压力分散至外部支护结构中，从而使得钻锚机械臂结构长期处于相对稳定的物理受力状态。连接器、连杆、启动器、固定装置作为机械臂元件的从属臂体成分，具备较强的弹性运动能力，可跟随主臂体成分的运行形式，更改固定装置的接入角度，避免明显运动误差行为的出现。帮锚结构、顶锚结构同时存在于智能机器人钻锚机械臂下端，能够根据从属臂体的连接形式，更改自身开合角度。

1.2 运动学参数模型

所谓运动学参数模型，是以运动学标定的方式，辨识出智能机器人钻锚机械臂各个节点处的参数指标，再根据已知的不确定性要素分析思想，对辨识得到的参数指标进行二次修正处理，可使已建立的运动学参数模型更符合实际应用需求，关节与末端执行器元件保持相同的运动趋势[2]。

在考虑不确定性原则的基础上，机械臂运动学参数模型标定的大体执行思路如下。首先，采集机械臂关节与末端执行器元件的运动行为，根据已知的不确定性指标，确定待标记参量的具体数值水平；其次，分别选取机械臂关节、末端执行器元件作为分析对象，建立待标记参量与既定机械臂运动学参数之间的数值映射关系；然后，借助不确定性系数指标，验证已知数值映射关系是否符合实际应用需求；最后，联合机械臂结构的实时运动位姿状态，对运动学参数模型进行修正处理。

设α表示机械臂帮锚结构与顶锚结构之间的物理夹角，g表示机械臂连杆的当前接入长度值，λ表示旋转杆转动系数。联立上述物理量，可将所选取的智能机器人钻锚机械臂运动学参数A表示为：

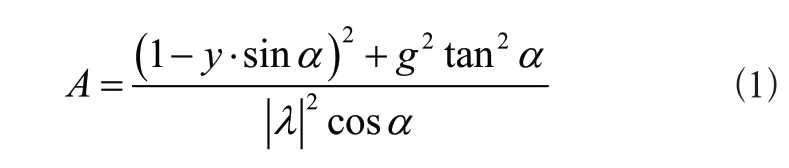
规定we表示不确定性标度系数为e时的机械臂运动指征向量，对于智能机器人钻锚机械臂运动行为而言，we∈A的取值表达式恒成立。β表示与机械臂结构相关的运动行为系数，r1、r2表示两个不同的运动学误差指标。在上述物理量的支持下，可将计及不确定性的智能机器人钻锚机械臂运动学参数模型表示为：

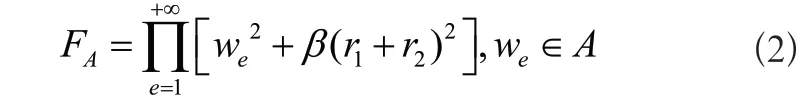
对于智能机器人钻锚机械臂的运动学参数标定处理，必须遵循运动学参数模型，且在实际运动过程中，帮锚结构与顶锚结构之间的物理夹角越大，机械臂组织的连续运动能力也就越强。

2 计及不确定性的机械臂运动学误差

在运动学参数标定原理的基础上，按照关节旋量定义、执行器末端位移误差计算、误差线性方程建立的处理流程，完成计及不确定性的智能机器人钻锚机械臂运动学误差分析方法的设计与应用。

2.1 关节旋量定义

为实现对智能机器人钻锚机械臂运动学误差的准确分析，可将关节元件的角度变化运动看作一种刚体约束性行为，在实际运算过程中，应将任何关节轴旋量偏差都视为一个刚体运动变量。对于智能机器人而言，机械臂关节旋量的刚体变换基本等同于伴随状运动变化行为，即随着机械主轴、连接器所处位置的改变，机械臂关节旋量的运动学行为也会产生变化，这在物理坐标系中，可被理解为一种特殊形式的线性变化状态[3]。若计及不确定性要素对伴随变换造成的影响，可将机械臂关节旋量及其相关误差指标定义成如下几个公式。

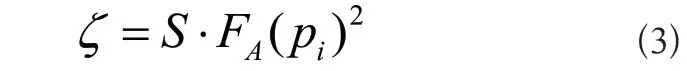
式(3)中，ζ表示机械臂关节元件旋量角度的刚性定义项，S表示主轴连接系数，i表示旋转系数，pi表示i取值条件下的连接器运动向量。

规定在如图2所示的关节旋量误差几何结构中，ε1、ε2、ε3三条基线都与唯一的辅助线保持对应性运动学关系，且每条辅助线的定义都具有一定的不确定性。

图2 关节旋量误差的几何结构

若以δ1、δ2、δ3分别命名三条辅助线，则可将机械臂关节旋量定义式表示如式(4)所示：

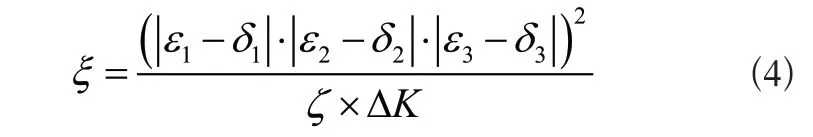
其中，ΔK表示单位时间内的关节转动角位移。在只考虑关节旋量误差的情况下，转动角的取值结果只能处于0～180°的物理区间。

2.2 执行器末端的位移误差

在不确定性要素的影响下，距离误差是由执行器末端元件的位姿偏差直接引起的，随着关节旋量取值结果的增大，执行器末端的位移误差水平也会逐渐增大，直至整个机械臂结构呈现出完全水平或完全竖直的存在状态。

规定b、m表示执行器末端两个不重合的运动点，其中，b点坐标为(xb，yb，zb)，m点坐标为(xm，ym，zm)。在基本位移系数为β的情况下，可将b、m之间的理论距离表示为：

规定b′、m′表示执行器末端两个不重合的静止点，其中，b′点坐标为点坐标为在静止系数为x的情况下，可将b′、m′之间的理论距离表示为：

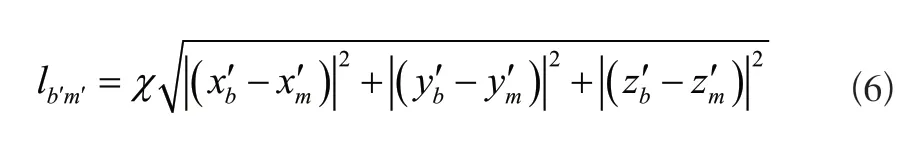
联立式(4)～式(6)，可将执行器末端的位移误差表达式定义为：

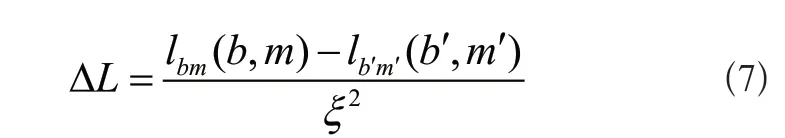
对于同一坐标系下的两组物理坐标而言，虽然它们所表现出的运动行为有所不同，但由这两组坐标点所决定的位移误差表达式却是唯一且固定的[4]。在已知关节旋量条件的前提下，智能机器人钻锚机械臂所表现出的运动行为越明显，执行器末端的位移误差取值结果也就越大，这样就可以通过总结误差值特性的方式，促使关节与末端执行器元件保持相同的运动趋势。

2.3 基于不确定性的误差线性方程

误差线性方程决定了智能机器人钻锚机械臂的运动行为能力。在计及不确定性要素的情况下，误差线性方程的构建受到机械臂关节位姿与执行器末端元件位姿的直接影响[5]。机械臂关节位姿是指由初始位置k0指向终止位置kn的物理向量，具体定义式如式(8)所示：

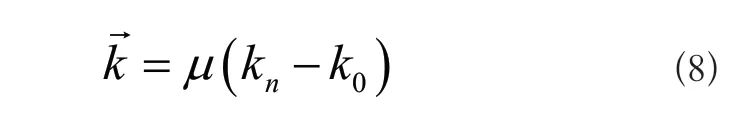
式(8)中，n表示关节位姿节点的个数值，μ表示与机械臂关节位姿相关的不确定性要素指标。

执行器末端元件位姿则是指由初始位置j0指向终止位置jn的物理向量，具体定义式如式(9)所示：

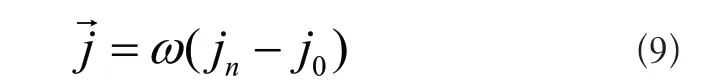
其中，ω表示与执行器末端元件位姿相关的不确定性要素指标。

规定智能机器人钻锚机械臂的运动行为始终符合线性计算原则，联立式(7)～式(9)，可将基于不确定性的误差线性方程定义为式(10)所示：

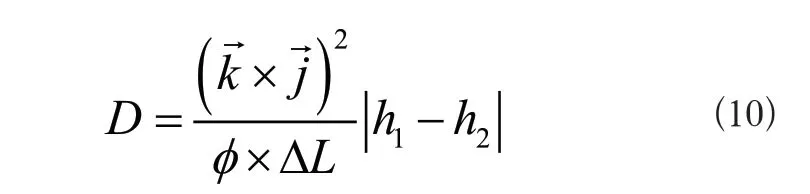
式(10)中，φ表示计及不确定性的运动学偏转系数，h1、h2表示两个不同的运动学误差标度值。至此，完成对各项指标参量的计算与处理，在考虑不确定性要素的情况下，实现智能机器人钻锚机械臂运动学误差分析方法的顺利应用 。

3 实例分析

选取如图3所示的智能机器人钻锚机械臂元件作为实验对象，分别应用计及不确定性的误差分析方法、自由度运动误差分析方法，对实验主机进行控制，其中前者作为实验组、后者作为对照组。

图3 实验操作原理

末端执行器元件与机器人主关节结构之间的运动关联度指标数值，能够描述机械臂结构的运动误差水平，关联度指标的数值水平越大，则表示机械臂结构的运动误差水平越小；反之，若关联度指标的数值水平越小，则表示机械臂结构的运动误差水平越大。

k指标代表机器人主关节结构的运动行为标度值，γ指标代表末端执行器元件的运动行为标度值，令配置实验组、对照组分析方法的机械臂元件同时搬运等重的货物，记录在此过程中，k指标与γ指标的具体数值变化情况。数值详情如表1所示。

表1 标度值指标数值

分析表1可知，随着搬运货物重量的增大，实验组k指标数值基本呈现出不断增大的变化趋势，且该指标的单位数值变化水平相对较为平均；实验组γ指标在实验前期始终保持稳定，当搬运货物种类超过40kg时，其数值水平开始不断上升。对照组k指标与γ指标的变化形式相对较为混乱，与实验组指标参量相比，其数值变化趋势并无明显规律。

已知末端执行器元件与机器人主关节结构之间运动关联度指标的计算表达式如式(11)所示：

规定本次实验过程中，D指标的取值结果始终为“1”。对应表1，计算实验组、对照组运动关联度指标的具体数值，详情如图4所示。

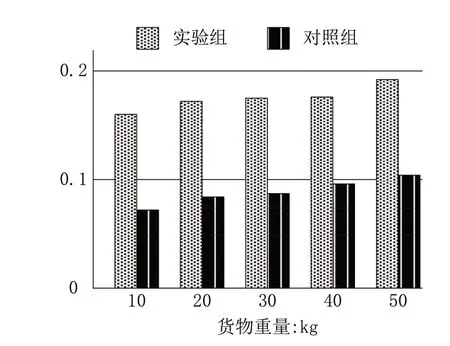
图4 运动关联度指标（10-50kg）

分析图4可知，实验组运动关联度指标的数值计算结果始终处于0.1～0.2之间，当获取重量取值为50kg时，实验组的运动关联度指标数值最大，为0.19575。对照组运动关联度指标的均值结果则始终小于实验组，当获取重量取值为50kg时，对照组的运动关联度指标数值最大，为0.1022。

分析图5可知，与图4相比，当货物重量取值处于60kg～100kg之间时，实验组运动关联度指标的均值水平更高，其最大值达到了0.23250。与图4相比，对照组的均值水平虽然略有升高，但依然低于实验组，其最大值也仅能达到0.10730。

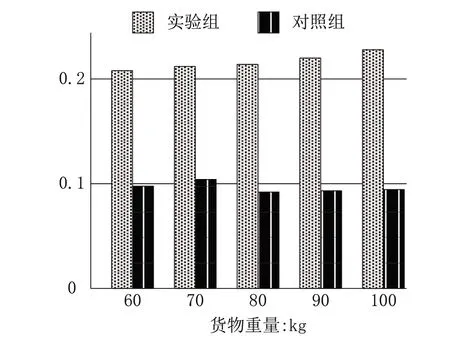
图5 运动关联度指标（60kg～100kg）

综上可知，与自由度运动误差分析方法相比，在计及不确定性误差分析方法的作用下，κ指标、γ指标的取值结果均出现一定幅度的上升，这对于增大末端执行器元件与机器人主关节结构之间的运动关联度指标数值，避免机械臂明显运动误差行为的出现。

4 结语

积极不确定性的误差分析方法，从智能机器人钻锚机械臂的运动学参数标定原理着手，在定义关节旋量、执行器末端位移误差的同时，建立完整的误差线性方程。实验结果显示，在这种新型分析方法的作用下，末端执行器元件与机器人主关节结构之间运动关联度指标的数值明显增大，不但能够促使二者保持相同的运动趋势，也可以避免智能机器人钻锚机械臂运动误差行为的出现。