Effect of conical intersection of benzene on non-adiabatic dynamics

Duo-Duo Li(李多多) and Song Zhang(张嵩)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China

2University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: conical intersection,nonadiabatic dynamics,ultrafast relaxation,quantum chemical calculations

1. Introduction

Born–Oppenheimer (BO) approximation is one of the fundamental approximations of atomic and molecular physics.[1]In the BO approximation,the electron and nuclear wave functions are separable because of their different time scales of motion,which makes up the premise for the adiabatic description of chemical reactions.[2]However,the BO approximation loses its effectiveness in some processes, such as ultrafast non-radiative relaxation, photodissociation, photofragmentation,chemiluminescence or isomerization of polyatomic molecules,etc.[3–6]For chemical reactions that occur in electronically excited states, non-adiabatic transition,[7–9]that is, the coupling between two close-lying adiabatic surfaces caused by nuclear motion is not only universal but also essential in many chemical processes and biological processes. In particular,the conical intersection(CI),in which two adiabatic surfaces cross in at least the two-dimensional coordinate, is accepted widely as the dynamic funnel for such non-adiabatic transitions.[10–13]Conical intersection plays a significant role in nonadiabatic dynamic behavior in terms of molecular structure and chemical reactivity.[14–17]

Benzene is selected for this study because although it has been studied extensively over many years,there are still some uncertainties regarding the dynamics. Owing to the ability to detect chemical behavior on a much shorter time scale, researches concentrate on the dynamic properties of benzene and its derivatives, such as its fluorescence lifetime, excited state relaxation,and photolysis.[18–30]It is noticed early that the fluorescence quantum yield of benzene drops sharply as the excitation energy is 3000 cm−1above the 0–0 transition energy of the S1state. This phenomenon has been explained by the effect of a CI between the S and S1states,which can promote non-radiative relaxation between electronic states. The lifetimes of vibronic sequencev6andv7in the1B2ustate were reported on a time scale of nanoseconds. Furthermore, the possible photochemical reactions caused by the effects of the S2/S1and S1/S conical intersections were inspected based on the MC-SCF calculations.[20]It is demonstrated that the occurrence of Dewar benzene as a product of the S2photochemistry is directly attributed to the efficient crossing via the conical intersection of S2/S1. Moreover, the origin of the low quantum yield (∼0.02) of photochemical benzvalene production from the S1results from the fact that most of populations decay and return to S benzene via S1/S conical intersection.Furthermore,the rapid decay of the S2state was measured to be about 50 fs by using time-resolved time-of-flight mass spectrometry and photoelectron spectroscopy experimentally.[31–35]Moreover,the arrival times of the wavepacket from the S2state to the S1and S states are 64 fs and 68 fs by VUV time-resolved photoelectron spectra,respectively.[36]It is considered that most of the populations in the S2state decay directly to the S state and are not detected in the S1state.And it is also pointed out that a small number of the populations do get trapped in the S1state and the conversion of the S2state into the S1state is only about 1%,[33,34]while the yield of S2→S1estimated from the timeresolved photoelectron imaging is much greater than 10%.[31]In addition, the long lifetime of the S1state conversion into the S state was measured to be 6.5, 6.7, and 7.6 ps given in Refs.[31–35],respectively. Furthermore,the excited state direct dynamic behaviors in the S2state and the S1state with quantum calculations were illustrated,and the mechanisms of internal conversion were revealed. It is concluded that the relaxation of the S2state is very fast via the S2/S1intersection and the following population on the S1state decays much more slowly via the S1/S intersection. The precise branching ratio between the populations in the two excited states would require a more detailed investigation of the topological geometries.

In this work, the energy values, structures, and orbits of the ground state and the excited states are determined by using the multi-configuration complete active space self-consistent field (CASSCF) theory.[37]At the same time, the topological structures and energy values of the S2/S1and S1/S conical intersections are also obtained. These results are conducive to explaining and clarifying the photophysical behavior of benzene excited to the S2state and the effects of the S2/S1and S1/S conical intersections.

2. Calculation methods

The photochemical dynamics of benzene have a high degree of multi-configuration due to the multiple electronic states with many degeneracies and near degeneracies due to the presence of conical intersection. The CASSCF methods were employed to study the relaxation path of the excited states of benzene. The static electronic structure calculation was carried out by the CASSCF(6, 6) method with the basis set 6-31+G(d, p) through using Gaussian 09 software.[38]In order to clarify the relaxation process of theππ∗excited state,it is necessary to select theπcharacteristic orbits and exchange thenorbit of HOMO-2[the highest occupied molecular orbit(HOMO)]with theπorbits of HOMO-4. The final activation space is composed of six electrons and six orbits(i.e.,threeπorbits and threeπ∗orbits). The energy values,structures,and the orbit of the ground state and orbits of the excited states are calculated. Finally, the CIs of S2/S1and S1/S are determined by scanning along the C1–C2–C3–C6 dihedral angle,and the structures, energy values, and orbits are all obtained. Moreover, the energy values of some critical points are obtained based on the CASPT2 method with the same basis set.

3. Results and discussion

The geometries of the ground state and excited states are optimized by the CASSCF(6, 6) method with the 6-31+G(d,p) basis set and illustrated in Fig. 1. The optimized structures of the S0, S1, and S2states are all planar withD6hsymmetry. The length of C–C bond and C–H bond in the S0state are calculated to be 1.398 ˚A and 1.076 ˚A at the CASSCF(6,6)/6-31+G(d,p),respectively.And the C–C bond lengths of the S0state are calculated to be 1.394, 1.37, and 1.39 ˚A by the methods of RASSCF(6, 1+5+6)/6-31G(d),CASSCF(6, 6)-PT2/6-31G(d), and CASSCF(6, 5)/6-31G(d),respectively.[39,40]In addition, according to the calculation by the CASSCF(6, 6)/6-31+G(d, p) method, the length of the C–C bond and C–H bond of the S1state are 1.435 ˚A and 1.074 ˚A, respectively. And based on the calculations by the methods of RASSCF(6, 1+5+6), CASSCF(6, 6)-PT2/6-31G(d), and CASSCF(6, 5)/6-31G(d), the C–C bond lengths of the S1state are determined to be 1.432, 1.43, and 1.47 ˚A,respectively.[39,40]The calculated geometry of the S0state and the S1state are in agreement with the previous results. However,two different structures of the S2state,i.e.,a boat-shaped and a plane structures, are discovered with the RASSCF(6,1+5+6)/6-31G(d) and SCF/4-31G[39,41]It is interesting that three minima at the S2state were also mentioned by employing the RASSCF method.[30]However, our calculations confirm that a plane geometry is more stable, which is consistent with the previous planar structure.[39]In addition,the C–C bond length of the S2state is also consistent with the values of 1.415 ˚A and 1.414 ˚A calculated by the CASSCF(6,6)/6-31+G(d,p)method and RASSCF(6,1+5+6)/6-31G(d)method,respectively.[39]

Fig. 1. Optimized geometries of (a) ground state S0, (b) the first excited state S1, and (c) the second excited state S2 based on CASSCF(6,6)/6-31+G(d,p). Bond lengths are all in unit ˚A.

Figure 2 shows the six selected orbits. The HOMO-2 to HOMO orbit and the LUMO[the lowest unoccupied molecular orbit(LUMO)]to LUMO+2 orbit areπorbit andπ∗orbit,respectively. The excited states S1and S2are both optically brightππ∗state. The S1state is predominantly a transition from the e1gorbit to the e2uorbit, while the S2state arises from the transition from the e1gorbit to the e2uorbit.

Fig.2. Six selected orbits: π obits(upper),and π∗orbits(lower).

The adiabatic excited energy values of S1and S2states are calculated to be 4.608 eV and 6.889 eV, respectively.And the vertical energy values of the S1state with 5.020 eV and 4.755 eV obtained by the CASSCF(6,6)/6-311G+(d, p)method and the CASPT2/6-311G+(d,p)method. The vertical energy values of the S2state obtained by the CASSCF(6,6)/6-311G+(d,p)method and the CASPT2/6-311G+(d,p)method are both 7.307 eV.The previous experimental values of the S1state are measured to be 4.722,[42]4.75,[31,33]and 4.9 eV.[40,43]Simultaneously, the energy values of the S2state are measured to be 6.05 eV[33,44]and 6.2 eV.[39,40]Based on the different methods, the energy values of the two excited states are summarized in Table 1. Our result of the S1state is slightly lower than the other calculations but closer to the experimental values. However, the energy values of the S2state are 6.159 eV and 6.537 eV obtained by the method of PBE1PBE/6-311G++(3df, 3dp)[45]and the calculations by the method of CCSD/aug-cc-pVTZ-CM2[46]are closer to the experimental values. The results of the S2state,calculated by the CASSSCF method,[37]are obviously higher than the experimental values. Since dynamic electron correlation effects are not considered,the higher excited state energy values calculated by the CASSCF method are different form the experimental values. While the vertical excitation energy values obtained at the CCSD and the CASPT2 levels are slightly lower than the values obtained by the CASSCF method and closer to the experimental value since the dynamic electron correlation effect is taken into consideration in the first two methods mentioned above.

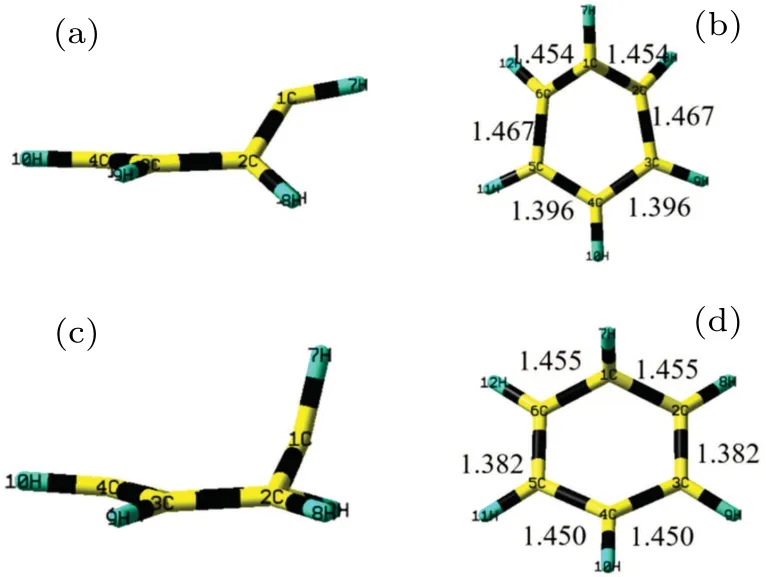
Fig.3. (a)Side view and(b)top view of optimized structure of S1/S0 conical intersection,(c)side view and(d)top view of optimized S2/S1 conical intersection. Bond lengths are in unit ˚A.

Table 1. Measured and calculated energy values(in unit eV)of excited states of benzene.

The optimal structures at the CIs of S1/S0and S1/S2are shown in Fig.3, and the detailed parameters of the bond distances, the bond angles and the dihedral angles are listed in Table 2. Our calculations reveal that the configures at the CIs of S2/S1and S1/S0no longer remain planar but evolves a half-boat-shaped structure along the out-of-plane coordinates.The distances of C2···C6 and C3···C5 bonds of the S1/S are 1.931 ˚A and 2.327 ˚A, respectively. And the C1–C2–C3–C6 and C4–C5–C6–C3 dihedral angles are 45.82◦and 3.894◦,respectively. The structure shape of S1/S0is similar to the previous calculated results.[26,40,44,47]According to the previous results, the distances of C2···C6 and C3···C5 were reported to be 1.92 ˚A and 2.33 ˚A by the method of CASPT2 and CASSCF(6, 5) with the 6-31G(d) basis set, respectively.The energy of the optimized structure at the CI of S1/S0is predicted to be 5.600 eV by the CASSCF method. It is only 0.992 eV higher than the minimum energy of the S1state. The energy at the CI of S1/S is determined to be 5.395 eV by the CASPT2 method, which is 0.205 eV lower than the value by the CASSCF method. Although the structures of the S2/S1are a boat-shape structure obtained by the CASSCF(6, 6)/6-31G(d)and CASSCF(6, 5)/6-31G(d)methods, our calculated structure of the S2/S1is confirmed to be a half-boat-shaped structure. The same structure is identified by the the method of RASSCF(6,1+5+6)/6-31G(d). The C2···C6 and C3···C5 bond distances of S2/S1are 2.443 ˚A and 2.488 ˚A,respectively.The C1–C2–C3–C6 and C4–C5–C6–C3 dihedral angles are 29.68◦and 10.29◦. In addition,the distances of C2···C6 and C3···C5 are about 2.46 ˚A and 2.49 ˚A at CASPT2/6-31G(d)and CASSCF(6, 5)/6-31G(d), respectively.[30]The bond distances C2···C6 and C3···C5 of the S1/S0are determined to be 1.931 ˚A and 2.327 ˚A,respectively,while the C2.C6 and C3.C5 bond distances of the S2/S1are determined to be 2.443 ˚A and 2.488 ˚A.It is concluded that the structure of the S2/S1becomes more slightly enlarged than that of the S1/S0and the warping degree of the S2/S1is not larger than that of S1/S0. The energy of the optimal CI of the S2/S1is located at 6.774 eV by the CASSCF method. It is obviously 1.174 eV higher than the energy of the S1/S0.The energy at the CI of S2/S1determined by the CASPT2 method is 6.590 eV,0.184 eV lower than that on the CASSCF method. With the half-boat-shaped the structure formed,the molecules lose their planar structures and their orbitals also change simultaneously. The corresponding orbitals of the S1/S and S1/S2are shown in Fig.4,respectively. Since the coupling of the orbitals occurs in the evolution of the relaxation,the orbital is no longer as regular as the shape in the Frank–Condon region. It is inferred that the changes in orbital properties of CIs are due to the reduced symmetry ofD6hand the coupling of states.

Table 2. Optical CIs (S1/S0 and S2/S1) structural parameters. Bond distances are in unit ˚A,and bond and dihedral angles are in degree.

Fig.4. Orbits of(a)S1/S0 and(b)S2/S1 conical intersections.

Time-resolved time-of-flight mass spectrometry and photoelectron spectroscopy experiments reveal that the relaxed lifetimes of S2and S1states are reported to be 50 fs and 6.7 ps, respectively.[31–35]Further, through the vacuum ultraviolet time-resolved photoelectron spectrum,the arrival times of S2at S1and S states are 64 fs and 68 fs, respectively,[36]which shows that the relaxation time of the S1state is very short. These experiments indicate that the decay of the S2state is so fast. Our calculations show that the S2/S1conical intersection is located at the out-of-plane bent structure near the minimum–energy structure of S2. The energy values of the S2state and the CI of the S2/S1are 6.889 eV and 6.774 eV,respectively. Since the energy value of the S2state is 0.115 eV higher than the energy value of the S2/S1, there is no potential barrier from the S2state to the S2/S1. This could explain that the relaxation process occurs on an ultrafast time scale with a lifetime of 50 fs after the excitation of the S2state, which is consistent with previous result. Reparameterization of PM3-FOMO-CASCI (6/6) predicts that the S2state decays to the lower excited states through CIs in a time of less than 100 fs.[40]It is mentioned that the different relaxation pathways are reported following the relaxation of the S2state. As described above, the CIs of the S2/S1and S1/S are both half-boat-shaped structures. It results in the fact that the wave packet will pass through the second CI immediately once passing S2/S1without undergoing significant structural changes. Simultaneously, since the energy value of the CI of the S2/S1is obviously 1.174 eV higher than the S1/S0,the large energy gradient will promote the direct internal conversion into the S0state. Although the direct relaxation to the S0state dominants, the branching ratio of at least 1% from S2to S1state is still indicated.[33,34]Specially, the yield of S2→S1is estimated at a value much greater than 10% by time-resolved photoelectron imaging with a time resolution of 22 fs.[31]Our calculations show that the energy difference between S2/S1and the minimum point of the S1state is as high as 2.166 eV.The high excess energy will preferentially make wave packet transfer to the minimum of the S1state. Furthermore, the energy of S1/S0is only 0.992 eV higher than the minimum energy of the S1state. Following arriving at a minimum value of the S1state,the wave packet carrying the excess energy overcomes the lower potential barrier and decays to the S0state through the CI of S1/S0.Furthermore,since the geometry changes from a planar structure on the S1minimum point to a half-ship structure of S1/S0,the indirect relaxation to the S0state is slow along multiple CIs paths. Accurately,the long lifetime decay of the S1state to the S0state is observed in the experiment. It is unfortunate that the quantum yields of the relaxation channels cannot be obtained in the present calculations.

4. Conclusions

The multi-configuration complete active space selfconsistent field method of the excited states of benzene provides important insights into the internal conversion mechanism. Based on the CASSCF(6, 6) method with 6-31+G(d,p) basis set, the minimum–energy structures of S, S1, and S2states are optimized to be planar structures. The adiabatic energy values of the S1and S2states are estimated at 4.608 eV and 6.889 eV, respectively. Simultaneously, optimized structures of the CIs S1/S and S2/S1are both half-boat structures.Although the structures of CIs S1/S and S2/S1are similar,the structure of S1/S is narrower and more warped than that of S2/S1. The energy values of S1/S and S2/S1are predicted to be 5.600 eV and 6.774 eV, respectively. Owing to the small difference in energy and the similar structures between the conical intersections of S2/S1and S1/S, wave packet directly decays to the S state through the two CIs after the excitation of the S2state. And this relaxation proves to be dominant.Our calculations also pointed out that a small fraction of wave packet relaxes to a minimum value of planar S1state through the CI of S2/S1. The subsequent wave packets with excess energy can cross the barrier of the CI of S1/S of the S1state. It takes longer time for the geometry to change from the planar minimum structure of the S1state to the CI of S1/S0.

Acknowledgements

Project supported by the National Key Research and Development Program of China (Grant No. 2019YFA0307700)and the National Natural Science Foundation of China(Grant Nos.11974381,11674355,and 21773299).