变均方根随机振动-变加速度离心复合试验

康 甜，欧 峰，严 侠，李明海

（中国工程物理研究院 总体工程研究所，绵阳 621999）

0 引言

飞行器再入飞行时，气动力会诱发强烈的振动和过载环境，对飞行器的结构完整性和功能有效性构成严峻挑战。为实现对飞行器的全动作流程考核，复现飞行力学环境效应，需要在地面试验中尽量真实地模拟再入飞行过载及振动力学环境的复合特性和时变特性。

当前，地面试验中的飞行过载-振动环境复合模拟主要有振动-离心复合试验和火箭橇试验2 种手段。美国Sandia 国家实验室从20 世纪70 年代以来，持续提升其振动-离心复合试验能力，并应用于洲际弹道导弹中弹道敏感组件、引信以及弹头的复合环境试验考核。我国的振动-离心复合试验技术发展较晚，2014 年才形成了可以模拟飞行力学环境的加速度-高频振动复合环境试验系统，并陆续开展了多类产品的过载-振动复合环境试验研究。上述试验研究均为恒定/缓变过载或稳态振动的复合，没有同时模拟两类飞行力学环境的时变特性。在火箭橇试验的飞行过载-振动复合模拟方面，以过载的时变特性模拟为主，没有要求振动模拟与飞行环境特性一致。

过载和振动环境时变特性的同时模拟需要有具备相应加载控制功能的试验设备和与之匹配的试验条件设计方法：试验设备的关键是解决激振装置适应动态离心场的问题；试验条件设计的关键则是提取出试验设备可模拟的、具有考核意义的时变特征量。

本文利用中国工程物理研究院总体工程研究所自行研制的具备过载、振动时变特性同时模拟功能的飞行过载-振动一体化动态模拟试验系统，开展再入飞行器子系统的变均方根随机振动-变加速度离心复合试验条件设计研究，以及复合试验控制验证。

1 再入飞行过载-振动力学环境

如图1 所示，某再入飞行器中包含2 个结构上相互独立但功能上相互关联的子系统，其功能动作由其中的过载环境敏感组件感知沿再入方向产生的轴向过载环境进行触发。为了实现2 个子系统的全动作流程考核、真实还原再入飞行过程中的潜在失效模式，需要按实际飞行环境同时模拟再入过程中轴向过载和轴向振动的时变历程。

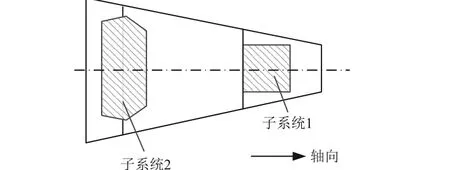
图1 某再入飞行器子系统示意Fig. 1 Illustration of concerned re-entry vehicle subsystem configuration

图2 和图3 分别为某次飞行试验中2 个子系统的轴向过载和轴向振动环境，图中的横、纵坐标均进行了归一化处理（下同）。图2 所示为飞行器质心处的轴向加速度随时间的变化，飞行器无摆动则2 个子系统的轴向加速度与质心处相同。图3 所示为2 个子系统安装位置测点振动响应的总均方根加速度随时间的变化，对应的频率范围为9～2240 Hz。

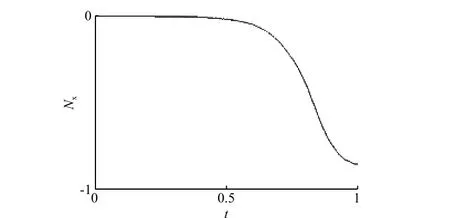
图2 再入段轴向过载环境Fig. 2 Axial inertial acceleration during re-entry

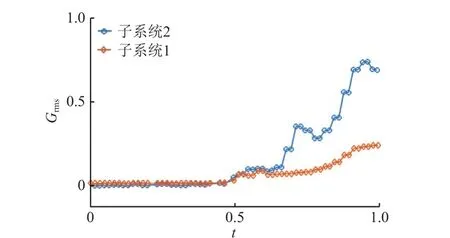
图3 再入段轴向振动环境Fig. 3 Axial random vibration during re-entry

本文以再现图2、图3 所示的过载、振动历程为目标，开展变均方根随机振动-变加速度离心复合试验研究。

2 变加速度离心试验条件设计

再入飞行器主要受轴向过载环境作用，要模拟的变加速度过程的附加切向加速度量值较小且不影响试验目的，因此可以不进行试件的多轴旋转控制，仅通过控制离心机转臂的转速来实现轴向加速度量值的变化，以降低试验系统的复杂程度。

变加速度离心用加速度序列进行描述，包含时刻和对应的加速度值。变加速度离心试验条件设计中的核心内容是确定加速度序列。本文利用图2 所示再入段轴向过载数据进行变加速度离心试验条件设计。先对轴向过载数据进行5 点滑动平均的平滑处理，以消除不影响试验目的且幅度较小的过载值波动。弹道数据的时间间隔为10 ms，相当于进行了上限频率为20 Hz 的低通滤波。低通滤波的上限频率是根据过载变化率确定的——过载变化率越大，则滤波的上限频率越高。应用低通滤波算法时须注意保持相位不变。

对平滑后的过载数据进行重采样，以增大试验条件中加速度序列的时间间隔，减少评判数据量。重采样时以两点间数据能够按线性插值进行恢复为前提，不是严格的等间隔采样。线性拟合的残差在控制容差的10%以内则不会影响实际加载控制的效果。

图4 给出所设计试验条件和实际过载的对比：在图示尺度下，试验条件的加速度序列与实际过载值完全重合，从过载变化率的对比可以看出平滑和重采样的处理效果。图5 为试验条件的局部放大，可以看出试验条件消除了小幅波动。

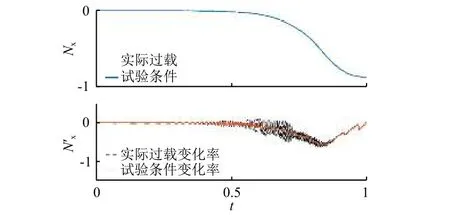
图4 变加速度离心试验条件与实际过载的对比Fig. 4 Comparison between the variable centrifugal acceleration test condition and the real acceleration load

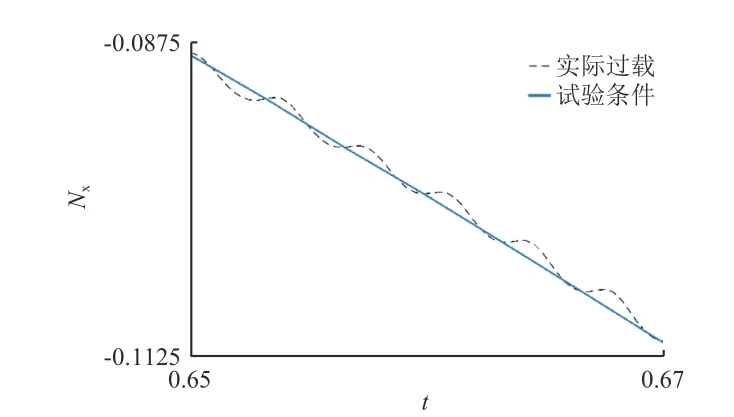
图5 试验条件的平滑处理Fig. 5 Smoothing of the test condition

3 变均方根随机振动试验条件设计

对振动环境时变特性的模拟，目前应用较多的是时域波形再现技术，但需要有实测的加速度时域数据。而此次飞行试验中受到遥测带宽的限制，地面接收到的振动测试数据是经过弹上预处理的频谱数据，不具备进行时域波形再现的前提条件。

频域的非平稳随机振动模拟可以通过调制实现均方根值时变的非平稳过程。为了能够模拟实际振动的均方根加速度变化历程，本文根据非平稳随机振动的调制思想，采用变均方根随机振动进行模拟：在常规随机振动的基础上，将均方根加速度作为控制的“增益”；在保证控制谱频率特性不变的情况下，控制总均方根加速度随时间变化。这是频域控制方法实现非平稳随机振动的一种简化方式。

变均方根随机振动采用归一化频谱和均方根加速度序列来进行描述。归一化频谱是加速度功率谱密度按总均方根加速度进行归一化后的表征，积分值为1。均方根加速度序列由分段时间点和总均方根加速度组成。变均方根随机振动试验条件设计的核心内容是确定归一化频谱和均方根加速度序列。

本文利用图3 所示的实测振动数据进行变均方根随机振动试验条件设计。实测振动数据是经过1/3 倍频程预处理的频段内均方根加速度，下限频率为9 Hz。而低频振动测量会受到动态变化的过载环境的影响，故在开展动态离心-振动复合试验时，不需要模拟这部分的低频振动；选取中心频率80 Hz 以上的频段，计算出每帧数据频段内的平均加速度功率谱密度作为试验条件设计的输入，在双对数坐标下功率谱密度分布情况如图6 和图7所示，图中时间为归一化坐标。

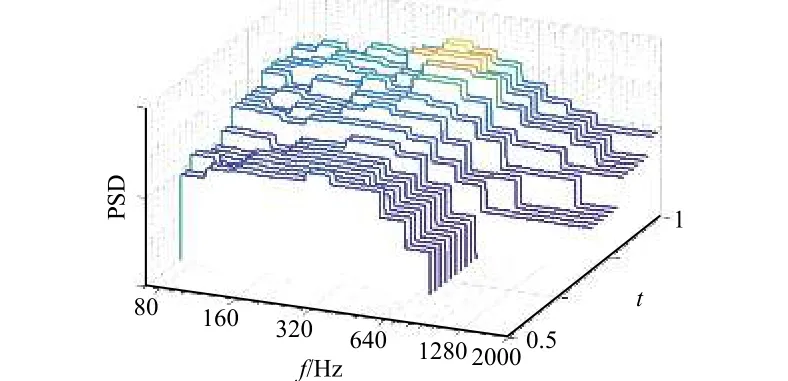
图6 子系统1 实测振动PSD 谱Fig. 6 The measured vibration PSD of subsystem 1 in flight

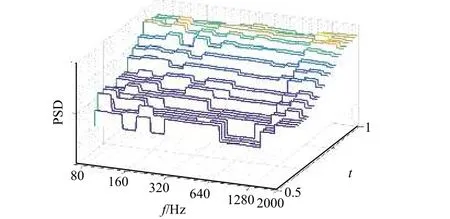
图7 子系统2 实测振动PSD 谱Fig. 7 The measured vibration PSD of subsystem 2 in flight

再入段前期振动量值小，测试数据主要为测量系统本底噪声，因此选取再入段后期信噪比达到2以上的测试数据来设计试验条件。

分段时间与遥测数据帧的时间长度保持一致。对每一帧频谱数据按式(1)进行归一化处理并提取出试验频率范围内的总均方根加速度。以各帧的总均方根加速度作为加权因子，按式(2)对各帧归一化功率谱密度进行加权平均，将加权平均后的谱作为试验条件中的归一化频谱。

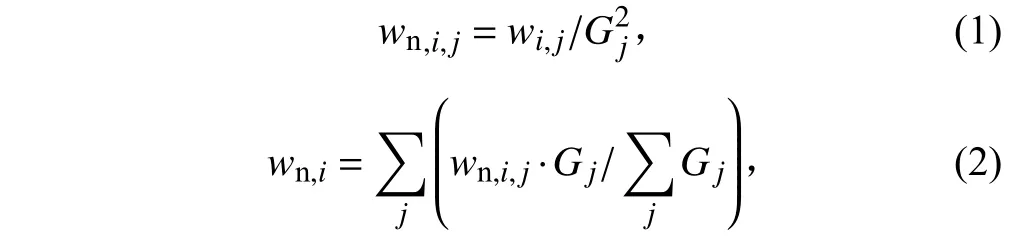
式中：为第帧、第个频段内的实测数据归一化功率谱密度，Hz；G为第帧的总均方根加速度，；为融合后，第个频段内的归一化功率谱密度，Hz。

图8 和图9 分别为利用子系统1 和子系统2 的振动测试数据处理得到的变均方根随机振动试验条件，其与实际振动环境的差异主要来源于试验条件未包含中心频率80 Hz 以下频段。图8、图9 中均方根加速度和时间为归一化坐标。

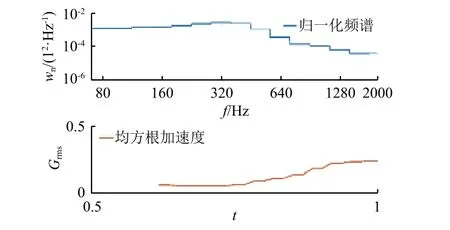
图8 子系统1 变均方根随机振动试验条件Fig. 8 Variable RMS random vibration test condition of subsystem 1

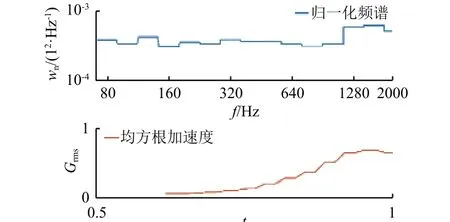
图9 子系统2 变均方根随机振动试验条件Fig. 9 Variable RMS random vibration test condition of subsystem 2

4 再入飞行器子系统复合试验

4.1 试验系统

飞行过载-振动一体化动态模拟试验系统如图10 所示，主要由GLJ-3R 三轴动态离心机、适应动态离心场的宽频激振装置以及时域振动控制系统等组成。该试验系统可实现50 kg 负载在15/s过载变化率下复合加载的随机振动均方根加速度达到6，具备波形再现和变均方根随机振动控制功能。试验对象在试验系统中的安装参见图10，振动测点位于2 个子系统的安装连接螺栓附近，振动加速度测量采样频率16.4 kHz；过载测点位于吊舱机械结构上，离心加速度测量采样频率10 kHz。

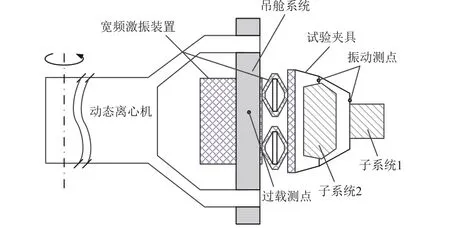
图10 飞行过载-振动一体化动态模拟试验系统和试验对象Fig. 10 The test system and the test items for the integrated dynamic simulation of flight overload and vibration

4.2 试验过程

采用图4 和图8 所示试验条件作为复合试验的加载条件。离心加载以子系统1 中的过载敏感组件位置为控制基准；振动加载以子系统1 安装位置为控制基准，通过试验夹具设计使得子系统2 安装位置的振动响应达到试验条件要求。振动加载是在离心机静止状态下通过反馈控制获得合适的驱动曲线后，当离心加载达到规定量值时，通过开环控制直接输出驱动实现的。由于振动条件的起始值不为0，在试验规定的起始时间之前增加了4 帧的时间来实现起振和平稳过渡，过渡段加载量值不超过试验起始值即可。

4.3 数据处理

由于离心控制基准位置与离心加速度测点位置的旋转半径不同，离心加速度测试结果按

进行修正。式中：为控制点的离心加速度；为过载测点加速度；为过载测点的等效旋转半径；为控制点的等效旋转半径。修正后的数据首先进行上限频率为20 Hz 的二阶巴特沃斯滤波处理，然后以离心加速度最大值时刻为标志与试验条件时间进行对齐，再按试验条件规定的时刻点进行数据抽取，计算出各时刻点上的相对偏差。

振动加速度测试结果以振动加载结束时刻为标志与试验条件时间进行对齐，按试验条件规定的分段时间划分数据帧，对每帧数据进行自功率谱分析，再按试验频率范围计算出每一帧的均方根加速度值。

4.4 试验结果

采用相同试验条件重复进行3 次试验，实现了振动历程和过载历程的同时模拟。离心加速度控制点的试验数据处理结果见图11；振动加速度控制点的试验数据处理结果见图12。可以看到：整个试验时间段内离心加速度与试验条件相比，最大偏差未超过±1%。在试验条件规定的振动加载时间段内，振动量值较小时，正偏差较大；振动量值增大后，偏差减小，均在±3 dB 以内。分析原因认为，在试验条件规定的加载时间之前，离心机工作的电气环境使得测量数据存在较大的本底噪声，而振动加载又是按照离心机静止状态下的驱动实施开环控制的，故而影响了低量值振动控制的测试结果。

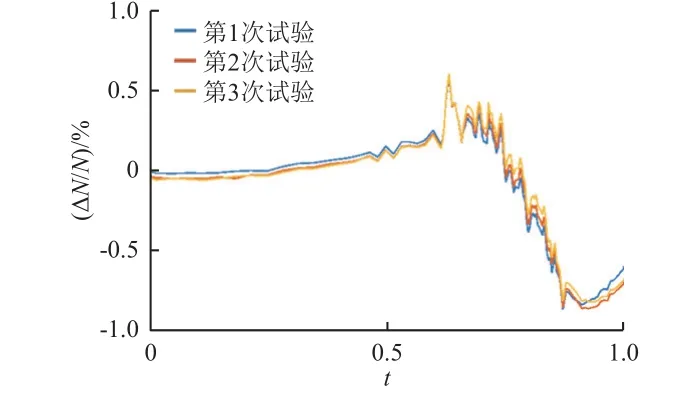
图11 复合试验中的离心加速度偏差Fig. 11 Centrifugal acceleration deviation in the combined test

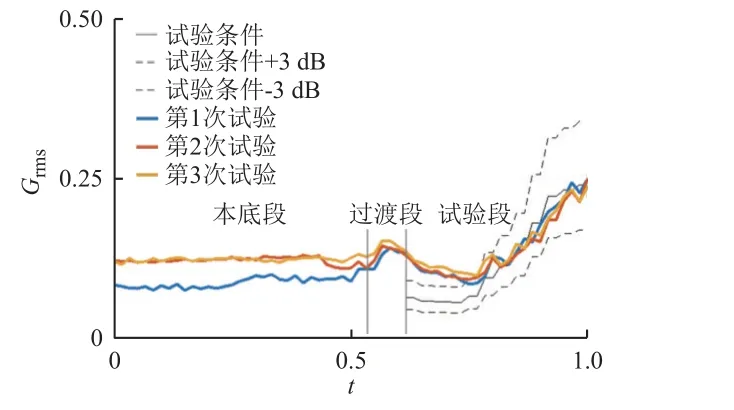
图12 复合试验中的随机振动均方根加速度Fig. 12 RMS acceleration of random vibration in the combined test

5 结束语

本文研究提出了一种变均方根随机振动-变加速度离心复合试验的试验条件设计方法，开展了再入飞行器子系统的复合试验验证，实现了在地面试验中对飞行过载和振动变化历程的同时模拟。这种试验方法对飞行器中惯性仪表等振动过载环境敏感组件的性能验证、误差修正建模等具有重要意义。后续还需开展三向动态过载与振动环境复合模拟的方法研究，以进一步提高地面试验中飞行力学环境模拟的真实性。