V 型皱褶芯材夹层板对流换热性能评价及优化

李丝丰，王志瑾

（南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016）

0 引言

热防护系统是高超声速飞行器不可或缺的重要组成部分，实现其防热-结构一体化将提升飞行器的结构效率和有效载荷。以胞元材料作为芯材的夹层结构不仅质轻，且具有可设计性，承载能力强，在散热、减振、隔声等多方面表现优异，常用于一体化热防护设计。将夹层结构与主动冷却相结合可以使结构具有更高的防热效率。

以超轻多孔金属材料为芯材的夹层结构是目前主动冷却式一体化热防护结构的主流构型，国内外学者对其冷却性能和优化方法已展开大量研究。Wang 等通过仿真和实验分析了3 种芯材杆件排列方式对夹层结构内流动阻力特性和换热性能的影响，发现杆件呈体心立方排列的点阵芯材夹层结构具有更高的主动冷却效率。徐亮等对点阵夹芯结构的换热性能进行评价，同时以杆件直径和倾角为设计变量，对金字塔和X 型点阵结构进行优化。Kemerli 等对Kagome 型点阵夹芯结构在恒定热流和恒定温度边界条件下的强制对流传热进行数值研究，分析了杆件尺寸对传热速率的影响。Rakow等研究了开孔金属泡沫夹层板在强制对流条件下的传热过程。孙雨果和高亮等研究了复合材料点阵夹芯结构在强制对流下的热传输特性，探索了流体流动特性对杆件倾角变化的响应。Khoshvaght-Aliabadi 等研究了具有不同流道曲线、不同截面形状的波纹夹芯结构在对流换热过程中的性能差异，并讨论了不同几何参数和流体组分的影响。

皱褶芯材是一种轻质、高比强度、高比刚度且具多功能潜力的新型芯材，研究其在主动冷却方面的应用，可为高超声速飞行器高效热防护设计提供新思路。黄盛等运用数值仿真方法对皱褶芯材夹层板进行流-固-热耦合分析，初步研究了该结构在强制对流情况下的对流换热特性。周晨和王志瑾等等进一步研究了V 型和M 型皱褶芯材夹层结构在特定条件下的换热性能和热应力分布，分析了芯材几何参数对流体流动的影响，并建立了V 型皱褶芯材用于被动防热的等效热传导预测方案。目前，针对强制对流条件下皱褶芯材夹层结构的研究主要集中在其对流换热特性以及芯材几何结构对流体流动的影响等方面，关于结构换热性能评价和优化策略需要进一步的研究。

本文以V 型皱褶芯材夹层板为研究对象，采用数值仿真的方法研究该结构在强制对流条件下的换热特性和流动阻力特性。利用Fluent 软件模拟基于流-固-热耦合的对流换热过程，得到流体域的温度场和速度场，并分析其换热特性和流动规律。探讨皱褶芯材夹层板中正三角和倒三角2 种流道的换热性能差异，提出相邻流道流体流向相反的优化方案。对比分析相同几何参数下的波纹芯材和皱褶芯材夹层板的对流换热性能，以及冷却剂流速对主动冷却性能和流动阻力的影响。定义一种新的综合考虑结构的冷却性能、冷却剂驱动功率和结构质量的换热效率指标，并以此为目标对皱褶芯材的几何参数进行初步优化设计。

1 模型设计及仿真设置

1.1 模型描述

皱褶芯材是将平板基材按照一定规律的线系网格进行局部折叠而得到的一种具有周期性胞元的立体构型（如图1 所示），与其他常见芯材相比，皱褶芯材具有多样化的构型和高度的可设计性，其内部空腔构成曲折的开环通道，向通道内通入冷却剂可实现主动冷却。

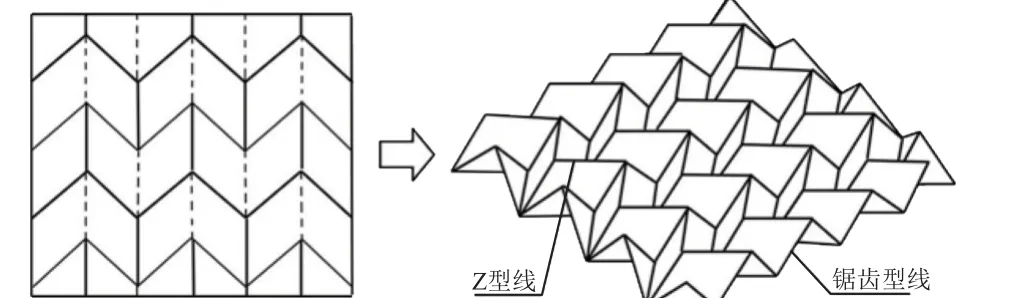
图1 皱褶芯材成型的几何示意[14]Fig. 1 Illustration of folded core forming

为模拟皱褶芯材夹层板作为热防护系统在飞行器上的应用，将热载荷施加在夹层结构的上面板上，向夹层板内部连通空腔内通入冷却剂进行主动冷却，如图2 所示。包含上、下面板的皱褶芯材夹层结构的周期性胞元如图3 所示，其中、和分别为上面板、芯材和下面板的厚度，胞元可由4 个独立参数（芯材高度、芯材截面宽度2、胞元步长2、皱褶偏折幅度）描述。本文所研究皱褶芯材夹层板几何尺寸的具体数值见表1。

表1 皱褶芯材夹层结构胞元几何尺寸Table 1 Geometric parameters of the cell in folded core sandwich structure单位：mm

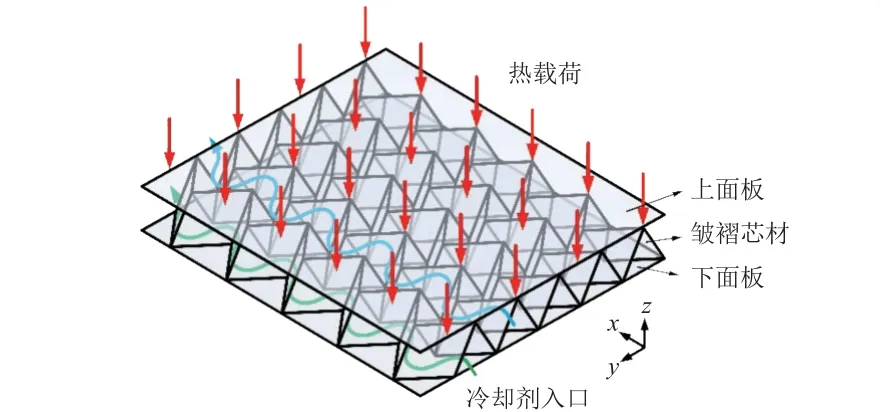
图2 热载荷条件下皱褶芯材夹层结构主动冷却过程示意Fig. 2 Active cooling of the folded core sandwich structure with thermal load

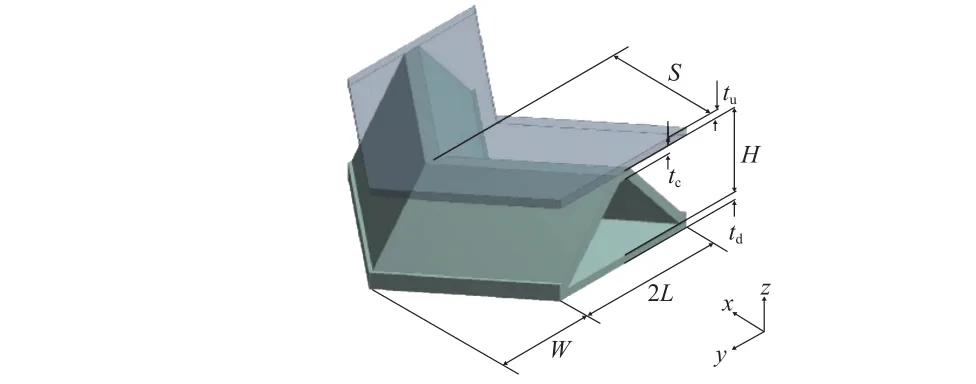
图3 皱褶芯材夹层结构胞元Fig. 3 A unit cell of the folded core sandwich structure

夹层板的上、下面板及芯材的材料均采用航空工业常用铝合金Al 2024-T851。冷却剂使用从燃料箱引入的碳氢燃料，可在实现主动冷却的同时对燃料进行预加热，提高其燃烧特性。为简化计算，忽略材料热物理性能随温度的变化，取室温下数值进行研究。材料的主要热物理性能如表2 所示。

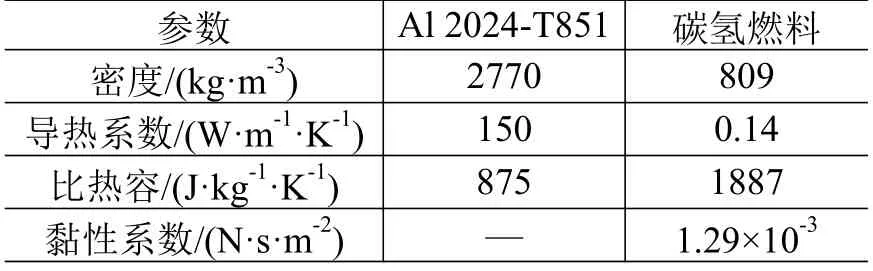
表2 材料热物理性能Table 2 Thermal physical properties of the materials

1.2 求解方法

强制对流条件下，皱褶芯材夹层板的传热过程包括：空腔内流体内部传热，固体结构的热传导以及流体与固体之间的对流换热。本文采用Fluent 软件模拟该共轭传热过程，对结构的温度场、压力场和速度场进行求解分析。数值模拟时假设：1）流动和传热是稳态的；2）流体为不可压缩的牛顿流体；3）不考虑结构与外部环境的自然对流和辐射换热。

皱褶芯材夹层板结构具有周期性，选取有代表性的部分进行计算便可以得出等效的整体结果。沿向取2 个周期、沿向（流向）取5 个周期共10 个胞元建立几何模型，简化后的模型如图4 所示。

图4 仿真计算用几何模型Fig. 4 Geometric model for simulation calculation

在皱褶芯材夹层板的上面板施加恒定的热流密度=100 000 W/m。流-固耦合界面采用Coupled无滑移、热耦合设置。其他壁面均设置为绝热壁面。在每个通路进口处沿向通入碳氢燃料作为冷却剂，其初始温度=300 K，进口流速=0.1 m/s，出口处设置参考压力=0。为了模拟整块夹层板的传热过程，在其向侧面上施加周期性边界条件。本研究通过雷诺时均法求解来获得稳态流场，湍流模型采用标准-模型。在近壁面处，选择增强壁面函数（enhanced wall treatment）处理。

1.3 网格近壁处理与网格独立性验证

使用ICEM 软件划分网格并对边界层区域网格加密处理。根据流场性质拟定，初始估算值为1，推算得到第1 层网格厚度后按图5 方案划分网格。

图5 夹层板模型网格划分方案Fig. 5 The meshing for the sandwich plate model

网格质量对数值模拟的准确性影响极大，为了减小误差，必须对网格独立性进行检验。图6 给出了平均努塞尔数随网格数量的变化曲线，可以看到在网格数超过1 000 000 后逐渐趋于稳定。平衡考量结果的准确性和计算的经济性，本文采用网格数为934 800 进行下一步分析，此时最大网格单元尺寸为0.8 mm。

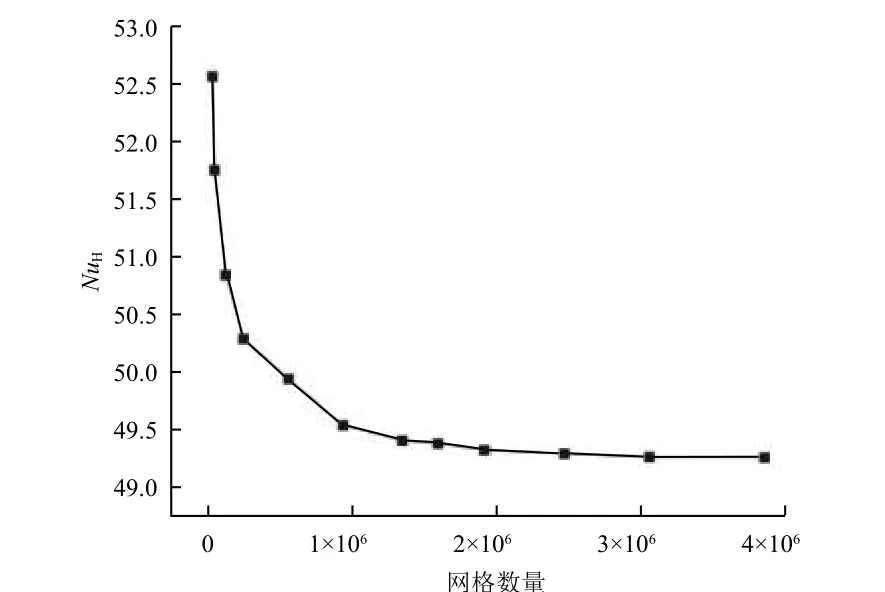
图6 平均努塞尔数随网格数量的变化Fig. 6 Variation of the average Nusselt number against the number of grids

2 对流换热性能分析

2.1 流场计算结果

图7 为流体区域紧靠上、下面板位置的速度分布云图；图8 为中间胞元在¯=0.5横截面上的流体速度矢量分布。由图7、图8 可知，经过进口段过渡后，流体速度随流道的曲折发生周期性变化：流体在拐角前贴近壁面处加速，在拐角尖峰处速度最大；经拐角处加速后，流体一部分以较大速度冲击下一个壁面，破坏该壁面上的附面层，另一部分发生回流形成涡流。

图7 流体区域紧靠上、下面板位置的速度分布云图Fig. 7 Velocity distributions of the coolant close to the upper and lower panels

图8 z¯ =0.5横截面上的流体速度矢量分布Fig. 8 Distributions of velocity vector on cross sectionz¯=0.5

图9 为流体区域紧靠上、下面板位置的温度分布云图。从图中可以看出，冷却剂流过通路，通过对流换热带走热量，温度逐渐升高。曲折管道使冷却剂流体不断地改变流动方向冲击壁面，减小了附面层厚度，同时产生的涡流增大了径向流动，使流体均匀混合，强化了对流换热效果。

图9 流体区域紧靠上、下面板位置的温度分布云图Fig. 9 Temperature distributions of the coolant close to the upper and lower panels

2.2 固体结构温度分布

图10 为稳态下皱褶芯材夹层板固体结构的温度分布云图；图11 为上面板、芯材和下面板的截面平均温度沿流向变化曲线。

图10 皱褶芯材夹层板固体结构的温度分布云图Fig. 10 Temperature contour for solid parts of the folded core panel

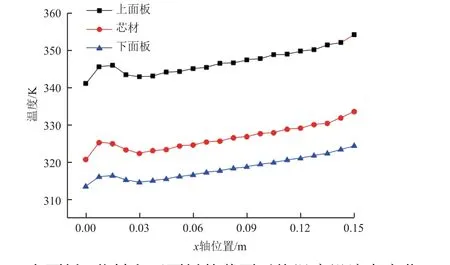
图11 上面板、芯材和下面板的截面平均温度沿流向变化曲线Fig. 11 Temperature distributions of the upper panel, the core and the lower panel along flow direction

由图10、图11 可知，结构截面平均温度沿流向逐渐升高，在进口段迅速上升后下降至一个低谷，随后平缓上升。这是由于冷却剂流体在进口段流动平缓，换热不够充分，使得进口段的固体结构温度迅速上升，经过流道偏折后流体换热能力得到增强，从而使固体结构温度的上升沿流向逐渐放缓。同时可以看到，在本研究中通过对皱褶芯材夹层板施加强制对流条件，有效减缓了热量由上面板向下传递的速率，使下面板维持较低的温度。

2.3 2 种流道的差异及改进

V 型皱褶芯材夹层板中的流道可根据其截面形状分为正三角流道和倒三角流道2 种。图12 为2 种流道中冷却剂温度沿流向变化曲线。可以看到：流道中冷却剂温度均在进口段大幅升高，在经过第1 次流道偏折后，呈现小幅度周期性波动的升高；同一截面位置，倒三角流道中的冷却剂温度明显高于正三角流道中的。这是由于在上面板上施加了恒定热流，而上面板直接构成倒三角流道的底面，使倒三角流道中的冷却剂流体与上面板大面积接触，对流换热效应最强，带走了大部分热量；还有一部分热量以热传导的方式通过芯材向下传递，再与正三角流道中的冷却剂进行对流换热。

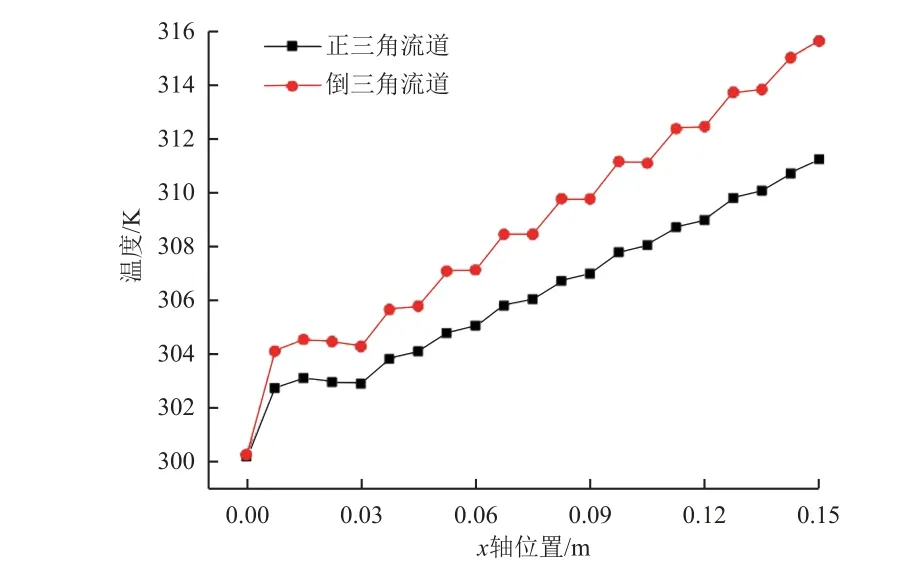
图12 2 种流道中冷却剂温度沿流向变化曲线Fig. 12 Temperature distributions of the coolant in the two flow channels along flow direction

位于底部的正三角流道中的冷却剂温度较低，为提高其利用效率，改变正三角流道中的冷却剂流动方向，使其与两侧相邻的倒三角流道中的冷却剂流动方向相反，如图13(b)所示。其他条件不变，将该流动方式与原流动方式（所有流道内冷却剂流向一致，见图13(a)）进行对比计算，得到如图14 所示的不同流动方式下的夹层板上面板温度沿流向变化曲线。由图14 可以看出，与流向一致的方式相比，流向相反方式的上面板温度变化梯度较小，温度分布更均匀。将不同流动方式下皱褶芯材夹层板各单元的最高温度整理成表3，可以看到，流向相反时夹层板各单元的最高温度有所降低，说明该流动方式使换热更均匀，提高冷却剂的利用效率。皱褶芯材夹层结构沿流向的温度梯度有所减小，使结构内部热应力减小，从而减轻结构的承载压力。

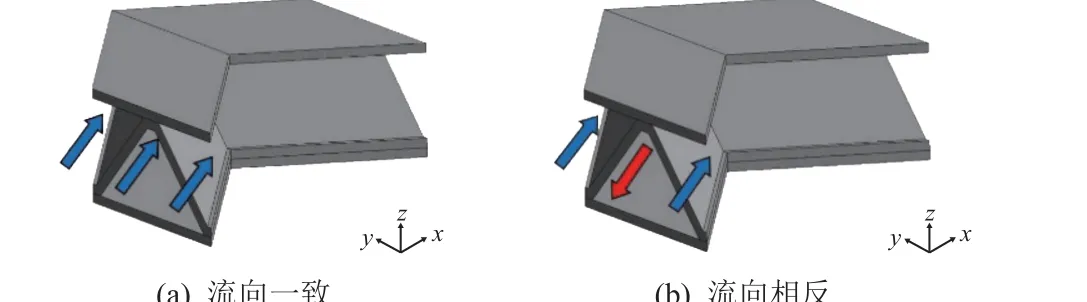
图13 2 种冷却剂流体流动方式Fig. 13 Two flow modes of the coolant fluid

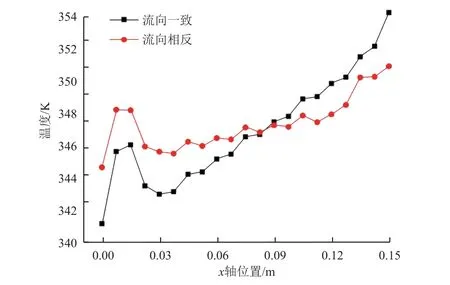
图14 不同流动方式下夹层板上面板温度沿流向变化曲线Fig. 14 Temperature distributions of the upper panel along the flow direction in two flow modes

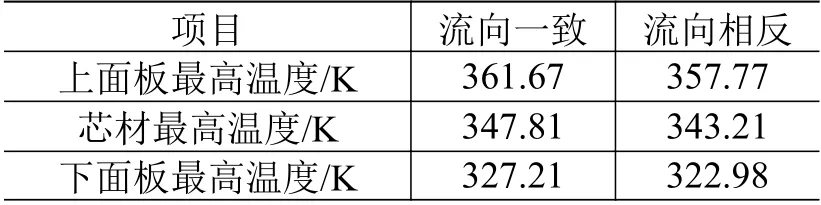
表3 不同流动方式下皱褶芯材夹层板各单元最高温度Table 3 Maximum temperature of each component of the folded core sandwich panels in two flow modes

2.4 与波纹芯材夹层板换热性能对比

当表征皱褶芯材曲折程度的参数趋于0 时，流道不再具有周期性偏折，曲折流道退化为平直流道，此时该构型可视为波纹芯材夹层板。在其他条件不变的情况下，取与上述皱褶夹芯结构具有相同截面形状、几何参数的波纹芯材夹层板进行分析计算。图15 为2 种夹层板的上面板温度沿流向变化曲线。由图可以看出，波纹芯材夹层板上面板温度显著高于皱褶芯材夹层板上面板温度，且沿流向的变化更显著。这是因为波纹芯材夹层结构中的流道平直，冷却剂流体随着管路长度的增加附面层逐渐增厚，流道变窄，即使流体靠近管壁的部分温度已经很高，但流道中间的低温冷却剂不能与管壁接触进行充分换热，导致冷却剂的利用效率较低。

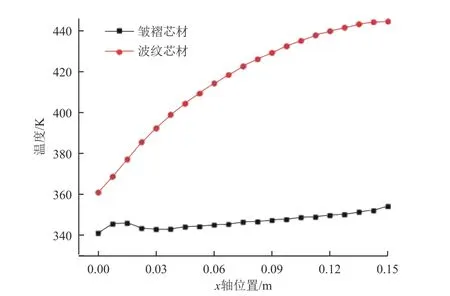
图15 2 种夹层板的上面板温度沿流向变化曲线Fig. 15 Temperature distributions of the upper panel of the two sandwich panels along the flow direction

流道构型的差异极大程度地影响着冷却剂流体的流动特性，从而导致对流换热效果的差异。而构型的改变还将导致结构质量的改变，定义皱褶芯材的当量密度为

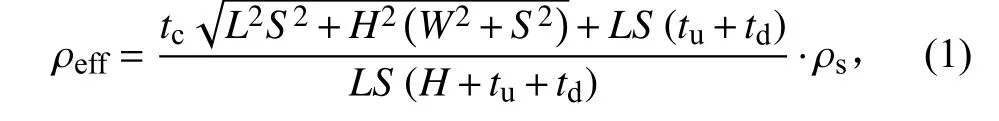
其中为结构材料（铝合金）的密度。计算时，波纹芯材可等效为=0 的皱褶芯材。

皱褶芯材夹层板与波纹芯材夹层板换热性能的计算结果如表4 所示。可以看到：与波纹芯材夹层板相比，皱褶芯材夹层板具有更好的换热性能；但皱褶芯材夹层板具有更大的单胞元质量，当量密度更大，且进出口压降损失较波纹芯材夹层板大得多，需要更大的泵功率来驱动冷却剂流动。

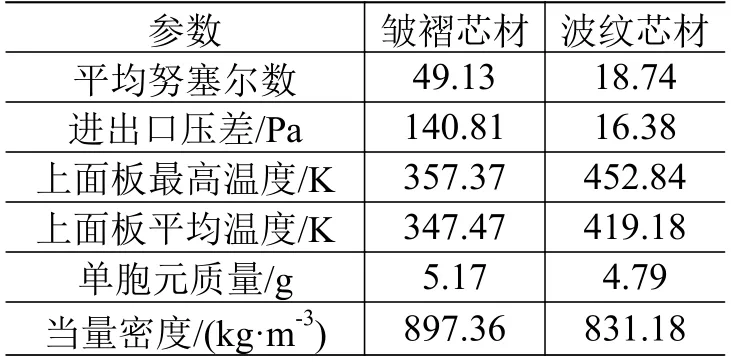
表4 皱褶芯材夹层板与波纹芯材夹层板换热性能对比Table 4 Comparison of heat transfer performance between folded core sandwich panel and corrugated core sandwich panel

2.5 压降损失的变化规律

在强制对流条件下，冷却剂的进口流速是影响主动冷却效果的重要参数之一，也决定了流道进出口压差，影响结构的承载能力和驱动冷却剂流动的泵功率。为研究不同进口流速对皱褶芯材夹层板和波纹芯材夹层板的换热性能和压降损失的影响，取不同进口流速分别进行计算。

图16、图17 分别为夹层板进出口压差和上面板平均温度随冷却剂进口流速的变化曲线。由图16可知，随着进口流速的增大，流道进出口压差逐渐增大，且皱褶芯材较波纹芯材压差升高的速率更大，这符合2 种流道的结构特性。由图17 可知，随着冷却剂进口流速的增大，上面板的平均温度逐渐降低，且降幅逐渐减小，在到达某值后趋于平缓。因此，设置冷却剂流速时应综合考虑进出口压差和冷却效果，选择一个合适的流速，在保证冷却效果的同时使泵功耗最小化。

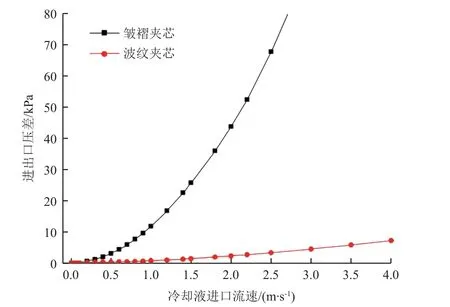
图16 进出口压差随冷却剂进口流速的变化曲线Fig. 16 Variations of pressure drop against inlet velocity

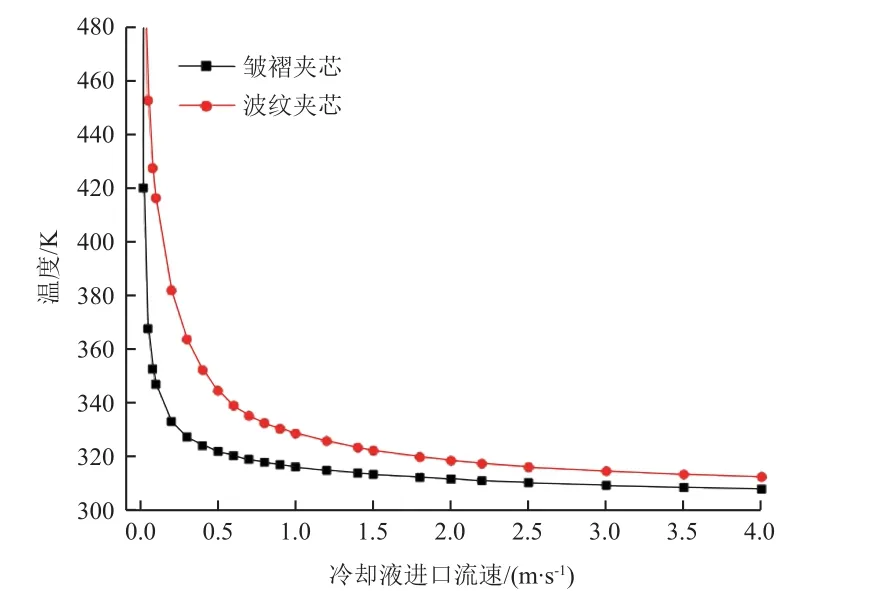
图17 上面板平均温度随冷却剂进口流速的变化曲线Fig. 17 Variations of average temperature of upper panel against inlet velocity

为进一步研究夹层结构的对流换热与流阻特性，以芯材高度为特征长度，引入雷诺数和文献[22]定义的用来表征流动阻碍作用的摩擦因子，

图18 显示的是雷诺数与摩擦因子之间的关系，对于皱褶芯材夹层板而言，在雷诺数小于2000的区域，阻力系数随雷诺数的增大而减小，流体流动受黏度的影响占主导；当雷诺数大于2000 时，流动实现了从黏度主导向结构形式主导的过渡，之后摩擦因子趋于一个稳定值。波纹芯材夹层板的压降损失较皱褶芯材的小很多，且在本实验的雷诺数范围内逐渐减小，压降损失始终受黏度主导。

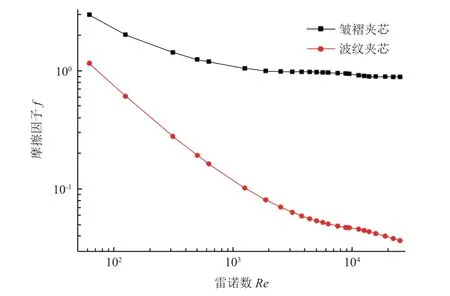
图18 摩擦因子和雷诺数之间的关系Fig. 18 The friction factor as a function of the Reynolds number

在对流传热研究中，充分发展段换热的整体特性可用实验关联式表示为

将不同雷诺数下计算得到的结果进行拟合，对于本研究中的结构，皱褶芯材夹层板与波纹芯材夹层板的实验关联式可分别拟合为=0.748和=0.072，拟合曲线与实验数值（实体点、块）在高雷诺数范围内一致性较高，如图19 所示。

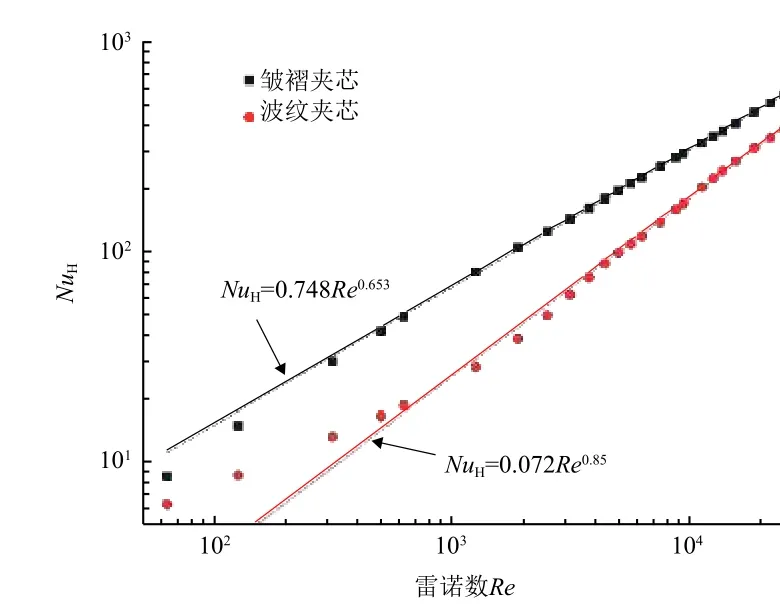
图19 平均努塞尔数和雷诺数之间的关系Fig. 19 The average Nusselt number as a function of the Reynolds number

3 换热效率评价及结构优化

3.1 热效率指标

改变皱褶芯材的几何参数可以得到不同构型的夹层板，为比较不同构型夹层板换热性能的优劣，需要引入热效率指标对其进行评价。热效率指标应综合考虑结构的换热特性、驱动冷却剂所需的泵功率以及结构的当量密度等，在不同需求下可调整各因素所占权重。

传统的热效率指标可表示为平均努塞尔数与摩擦因子的比值，

该指标既考虑了结构的冷却性能和驱动冷却剂所需的动力，又将结构质量考虑在内。

3.2 结构换热效率优化

皱褶芯材的众多几何参数为其构型设计提供了很大的空间，对这些参数进行优化可以使结构效率进一步提升。、、、是皱褶芯材的主要几何参数，其中和决定了结构的流道截面形状，和控制了流道的曲折程度。变动的会改变热防护结构的总厚度，因此将参数设置为定值，仅通过改变来控制流道截面形状。、、作为设计变量，控制其取值范围如表5 所示。

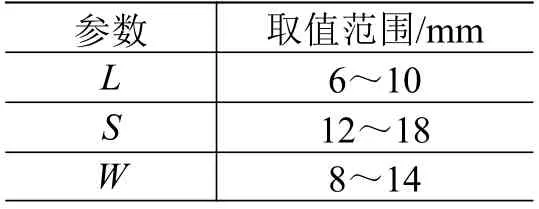
表5 结构几何参数取值范围Table 5 Ranges of the structural geometric parameters

采用优化的拉丁超立方取样法在设计空间中选取100 个样本点，计算努塞尔数、进出口压差和各单元温度等数值，根据样本点的计算结果建立Kriging响应面代理模型。为检测该代理模型的准确度，随机抽取10 个点进行检测，得到该代理模型的各项计算误差（以拟合优度系数表征，该系数值越大表示模型的计算误差越小）如表6 所示。可以看到，各项拟合优度系数均大于0.95，即该代理模型的拟合度较好，可以用来模拟结构的换热性能。

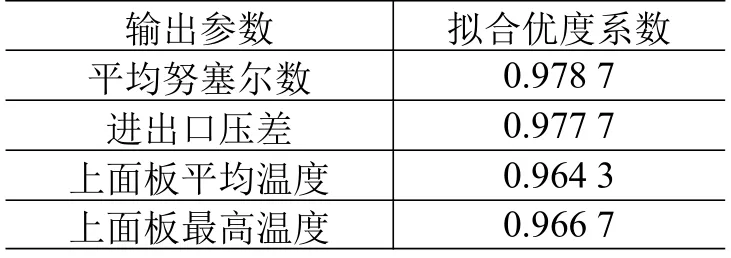
表6 代理模型计算误差Table 6 The errors of the approximate model

分别以上述4 种热效率指标为单目标函数进行无约束优化设计，即分别求解4 个优化问题：maxη，=1, 2, 3, 4。采用序列二次规划算法得到的优化设计结果如表7 所示。可以看出，以4 种热效率指标为优化目标分别求出的最优解数值比较相近，其中以为优化目标得到的最优解的值比其他优化目标的稍大，这是因为的定义中削弱了流动阻碍作用所占的权重。

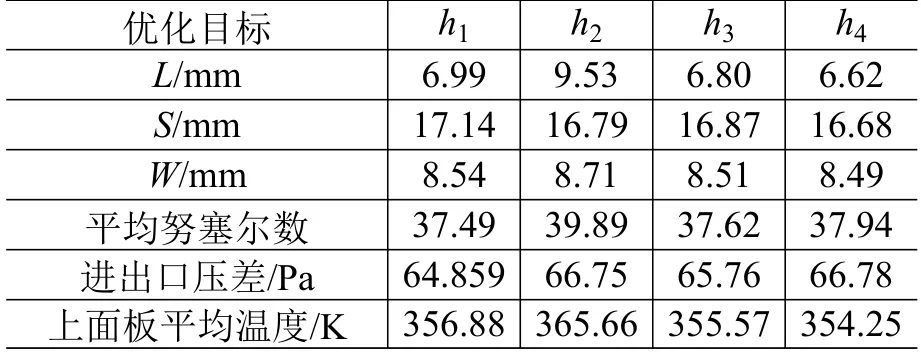
表7 以不同热效率指标为目标的优化结果Table 7 Optimized results with different thermal efficiency indexes as the target

4 结论

本文采用数值计算方法，对皱褶芯材夹层板在强制对流条件下的换热性能和流体流动特性进行研究，得到以下结论：

1）在强制对流条件下，皱褶芯材夹层板中的曲折流道使冷却剂流动方向发生周期性变化，冷却剂充分均匀混合并冲击壁面破坏附面层，增强了其与管壁的对流换热，有效减缓了热量向下面板的渗透。

2）皱褶芯材夹层板具有正三角和倒三角2 种流道，其中正三角流道中的冷却剂温度较低，未得到充分利用。为了提高冷却剂的利用效率，改变正三角流道中冷却剂的流动方向使与相邻流道中冷却剂的流动方向相反，可以降低夹层板结构的最高温度，减小结构温度梯度，使对流换热更均匀。

3）定义了一种同时考虑换热特性、冷却剂进出口压差和结构当量密度的热效率指标，以表征皱褶芯材夹层板在单位温差、单位功耗以及单位结构质量下耗散的热量。以多种热效率指标为目标对皱褶芯材的几何参数、、进行优化，找到了最优解，这些最优解具有相似的几何参数。