考虑压电耦合的空间充气展开结构频响特性分析

许素宇，李鹏飞，徐 超,2*

（1. 西北工业大学 航天学院，西安 710072； 2. 西北工业大学 太仓长三角研究院，苏州 215400）

0 引言

空间充气展开结构是由内腔含有超压气体的密闭薄膜组成的可收拢和展开的轻质结构，具有质量小、易展开、易存储等优点，能有效减小航天器载荷的质量和发射体积，解决大型空间结构发射困难的问题，并可显著降低大型空间结构的制造成本，因此在航天工程中得到广泛的关注和应用。

近年来，国内外已涌现出多种空间充气可展开结构，如充气式居留舱、充气式天线系统、充气式太阳电池阵等。充气结构展开后的结构自身刚度对空间系统整体的动力学特性有重要影响，因此采用仿真或实验方法准确获取充气结构的动态力学特性对空间结构的高可靠性设计至关重要。

在空间充气可展开结构动态特性仿真分析方面，有学者基于有限元方法对各类空间充气可展开结构的动力学特性进行了分析，但这些工作大多聚焦结构模态特性分析，很少涉及一定频率范围的稳态频率响应分析。

在空间充气可展开结构动态特性实验测试方面，大多仍采用传统实验方法——锤击法。然而，由于充气结构的自身柔性和带曲率表面几何特征，传统的激振和响应测量手段在应用时存在附加质量大、传感器不能共形贴附等问题。一种能更好地获取充气结构动态特性的方法是在充气结构表面粘贴轻质的柔性压电纤维复合材料（Macro Fiber Composite, MFC）作动器和传感器，利用主动压电激励获取结构关心频段内的响应特性。此外，柔性压电元件也被广泛应用于充气结构原位在线健康监测领域。

本文以空间充气杆为例，基于ABAQUS 有限元软件，考虑共形贴附在结构上的MFC 压电元件及其与充气结构的压电耦合作用，通过预应力分析研究充气压力的作用，在此基础上进行结构模态分析，并建立考虑充气预应力和压电耦合效应的结构动力学分析模型，采用直接积分方法获得结构的稳态频率响应特性。同时，开展基于柔性压电元件的充气结构频响特性测量实验，以对比验证仿真分析方法的有效性，并使用验证后的仿真方法研究充气压力对结构频响特性的影响。

1 充气杆频响特性分析

1.1 充气预应力分析

空间充气展开结构通常由内腔含有超压气体的密闭薄膜组成，薄膜材料多为聚酰亚胺（Polyimide,PI）。对于此类薄膜，可以采用ABAQUS 中的薄膜单元来建模，如M3D4R 单元（四节点四边形膜单元，减缩积分，沙漏控制）等。

空间充气展开结构内部需要保持一定的充气压力来确保结构刚度。因此，进行结构频率响应分析之前应考虑充气压力的预应力。为了在结构内部施加充气压力，需要定义流体腔，实际操作中选定充气薄膜内表面为流体腔表面，在内部取一点作为腔点，如图1 所示。流体腔的相互作用类型为气动类型，根据充气气体的不同设置理想气体分子量和充气压力，本文算例中选用空气作为充气气体。

图1 充气薄膜充气预应力分析建模Fig. 1 FE model of the inflatable film with prefilled gas

在所定义的流体腔施加充气预应力，进行静力学分析。基于膜结构的大变形特点，静力学分析时需要考虑流体腔的几何非线性，即结构刚度矩阵会随着载荷步迭代而变化，前一子步的应力状态会影响后续子步的刚度矩阵；这样到充气分析结束后，整体结构的刚度特性已纳入充气压力的预应力影响，后续压电耦合动力学分析中即以充气结束时的刚度矩阵作为结构初始刚度矩阵。

1.2 MFC 压电元件建模

MFC 压电元件具有高压电转化性能、高柔性及高可靠性等特点，一般由压电陶瓷纤维夹在胶层、电极和聚酰亚胺薄膜层之间组成。典型的MFC 元件如图2 所示，电极以互相交叉或者梳状模式附着在薄膜上，通过这些电极将电压施加到压电陶瓷棒上以及从压电陶瓷棒上输出电压。

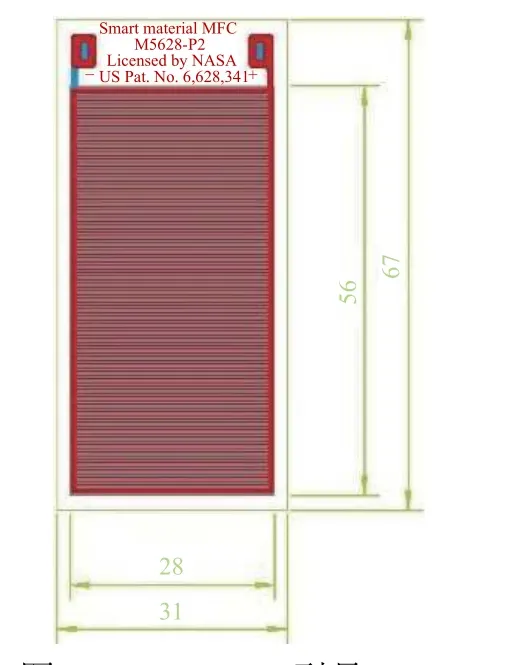
图2 M5628-P2 型号MFCFig. 2 MFC of the type of M5628-P2

压电效应原理是：压电材料在沿一定方向上受到外力的作用而变形时，其内部会产生极化现象，称为正压电效应；反之，在极化方向上施加电场，材料则会产生变形，称为逆压电效应。压电效应根据极化方向的不同分为效应和效应，本文采用的MFC 元件主要利用了压电材料的效应，即极化方向与应变方向垂直的纵向效应。MFC 材料的主要特性参数见表1。

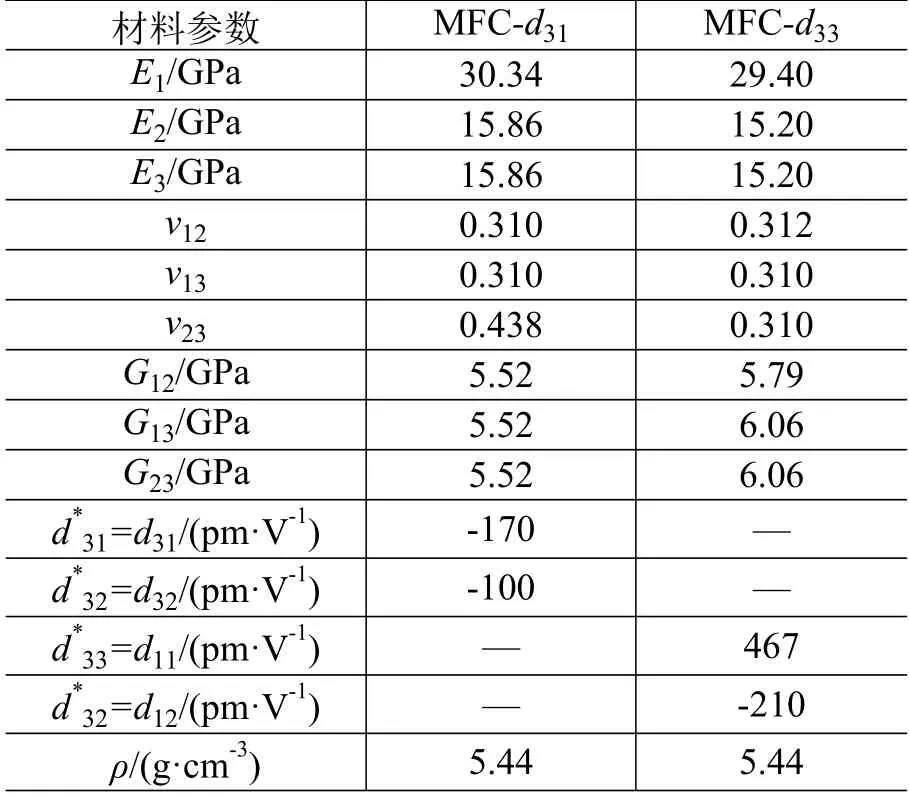
表1 MFC 材料主要参数[15]Table 1 Main parameters of the MFC material[15]

对于MFC 压电元件，可以采用ABAQUS 软件中的三维压电实体单元来建模，例如C3D8E（八节点线性压电六面体单元）等。但需要说明的是，由于本文使用的MFC 材料需要共形贴附到圆筒状的充气杆上，因此模型中的压电单元不是平面形状，需要重新为其指派材料方向，即采用单元坐标系描述压电材料的材料方向，如图3 所示。

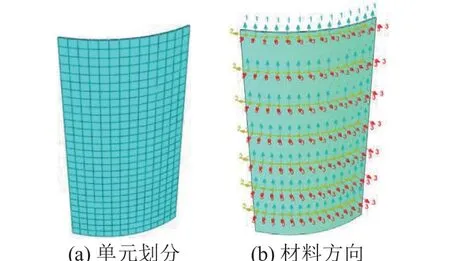
图3 MFC 压电元件有限元建模Fig. 3 FE simulation model of the MFC piezo-element

对于利用效应的MFC 压电元件，在压电片内外两面分布着梳状电极。在有限元仿真过程中，可为压电元件与空间充气展开结构粘贴接触的一面添加零电势边界条件，对压电元件的外表面施加正弦扫频电压信号，作为输入结构的激励。

1.3 频率响应特性分析方法

在建立了包含压电单元的耦合系统动力学有限元模型并获得了结构的充气预应力刚度的基础上，可进行关心频段内的稳态动力响应分析。

建模时已考虑压电耦合效应，故ABAQUS 软件采用直接稳态动力学积分方法在关心频段内的每个频率点对模型的原始微分方程直接积分，使用系统的质量矩阵、阻尼矩阵和刚度矩阵，根据模型的物理自由度直接计算获得系统的稳态谐波响应。

系统的阻尼定义可以采用全局阻尼定义，在ABAQUS 模型中直接通过*GLOBAL DAMPING,STRUCTURAL 来定义，具体输入的阻尼值可以根据实验结果估算得到。

1.4 小结

综合1.1～1.3 节所述的主要步骤，可以得到空间充气结构频响特性分析的基本流程，如图4 所示。

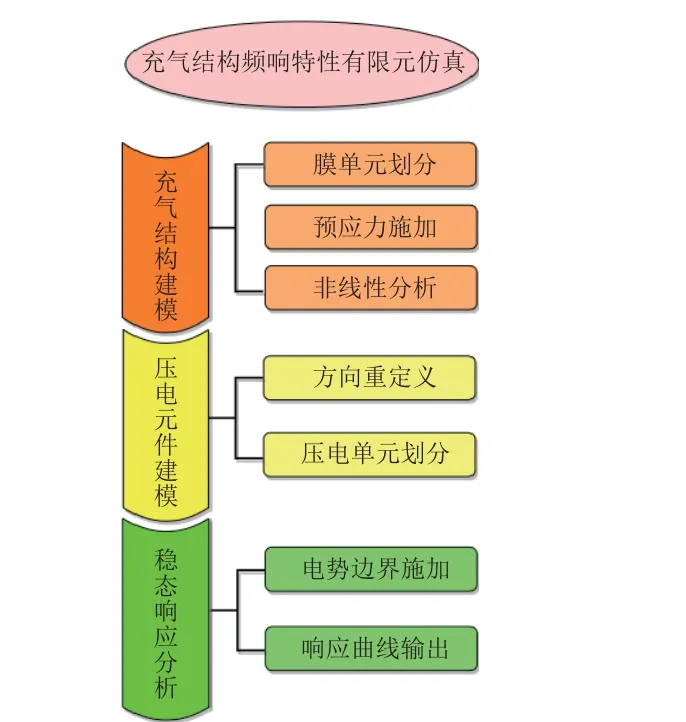
图4 空间充气结构频响特性分析基本流程Fig. 4 Flow chart of frequency response analysis of space inflatable structure

2 算例与实验验证

2.1 仿真分析

本文选取一个典型空间充气杆作为研究对象，杆高650 mm，外直径50 mm。如图5 所示，该结构由薄膜圆筒以及上、下端盖3 部分结构组装而成。其中，薄膜圆筒由厚度为15 μm 的矩形聚酰亚胺薄膜搭接而成，上、下端盖由聚乳酸高分子材料（PLA）3D 打印制造。两端盖圆外径均为50 mm，底座壁厚5 mm，带有4 条10 mm 厚的加强筋，并开有施加固支边界用的圆孔；顶盖壁厚3 mm。使用3M 公司的DP460 环氧树脂AB 胶将端盖与聚酰亚胺薄膜圆筒黏结起来。

图5 空间充气杆实体模型Fig. 5 Solid model of the space inflatable rod

根据空间充气杆几何模型的尺寸，简化上、下端盖后，建立其有限元仿真模型如图6 所示，其中MFC 压电元件采用C3D8E 单元，网格单元的近似全局尺寸为2 mm，单元数量为392 个，材料属性见表1；PLA 端盖采用C3D8R 单元（八节点线性六面体单元，减缩积分，沙漏控制），网格单元的近似全局尺寸为10 mm，单元数量为108 个，材料参数见表2；PI 薄膜圆筒采用M3D4R 单元（四节点四边形膜单元，减缩积分，沙漏控制），网格单元的近似全局尺寸为5 mm，单元数量为4160 个，材料参数见表2。

图6 空间充气杆仿真模型Fig. 6 Simulation model of the space inflatable rod

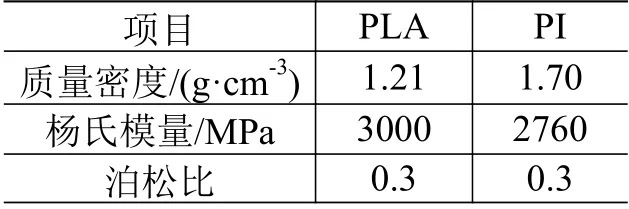
表2 PLA 及PI 材料参数Table 2 Material parameters of PLA and PI

有限元模型建立后，首先进行预应力分析：对结构流体腔施加0.02 MPa 的充气压力，获得结构的充压预应力刚度，充压后结构的应力和位移云图如图7 所示。从图中可以看出，在充气压力作用下充气薄膜不断张紧，产生了分布均匀的应力，最大Mises 应力为31.71 MPa；同时薄膜在压力下不断膨胀产生位移，最大位移为1.83 mm，出现在充气杆模型顶部。

图7 充气杆的应力和位移云图Fig. 7 The stress contour and the displacement contour of the inflatable rod

在预应力分析的基础上，对结构进行模态分析，获得充气结构的前5 个振动模态，如图8 所示。其中，前2 个振动模态对应整体结构的一阶弯曲振动，分别为和平面的弯曲振动。需要说明的是，由于粘贴MFC 压电元件的不对称性影响，这2 个弯曲振动模态的频率略有差别，分别为5.744 Hz和5.981 Hz。第3 个振动模态对应整体结构扭转振动；第4、第5 个振动模态对应整体结构的二阶弯曲振动。

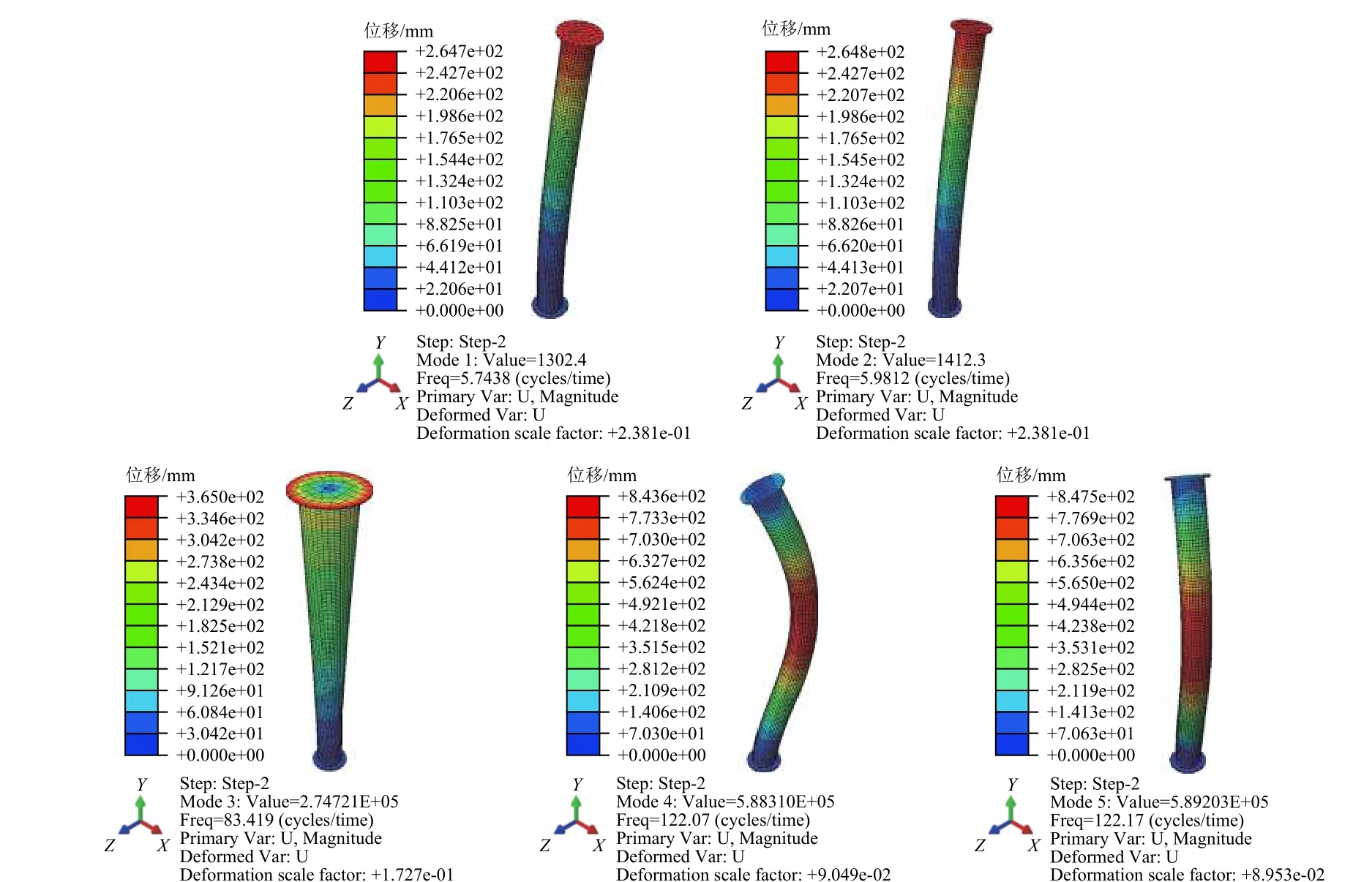
图8 充气杆的前5 个模态振型Fig. 8 The first five modal shapes of the inflatable rod

充气杆支撑结构在空间使用时，由于其自身柔性的限制，受到扰动易发生低频弯曲振动；同时考虑到实验室实验设备条件等限制因素，为便于将仿真结果与实验结果进行对比验证，本文主要对包含充气杆一阶整体弯曲振动模态的频率响应进行研究。前述分析表明该充气杆的一阶弯曲模态频率在5～6 Hz 之间，故后续频响分析中选择1～11 Hz频段进行对比验证。

2.2 实验验证

开展实验验证的目的是获取充气杆在压电激励元件作用下的频率响应特性，以验证仿真分析方法和结果。首先，为上述充气杆实体模型充压，充气压力保持在0.02 MPa。然后，将一片M5628-P2型号的MFC 压电元件通过环氧树脂胶沿充气杆径向粘贴在实验件底部往上10 cm 处，作为测量系统的激励元件。

激励信号采用步进式正弦扫频信号，激励能量集中，信噪比高，有利于获得高质量的实验结果。实验中，采用信号发生器产生激励信号，信号幅值±12 V，扫频范围1～11 Hz。

实验中使用激光测振仪测量充气杆的速度响应信号。由于聚酰亚胺薄膜的光反射率不能满足测量要求，需要在实验件的底部往上25 cm 处粘贴一片黑底白斑贴纸，以使激光测振仪能接收到较强的光信号。LMS 数据采集系统由信号发生器产生的电压信号触发，同时收集信号发生器产生的激励电压信号和激光测振仪采集的速度响应信号。采集系统将信号数据发送给计算机，在频域内计算出充气杆的频响特性。完整的充气结构测试实验平台如图9 所示。

图9 充气结构频响特性测试实验平台Fig. 9 Platform for testing the frequency response of inflatable structure

2.3 仿真分析与实验结果对比

取3 次实验测试结果进行平均后的频响曲线作为实验结果，与有限元仿真所得对应节点位置的频响曲线对比，如图10 所示。由图可见，空间充气杆的有限元频率响应仿真结果与地面实验结果符合良好，在所关心频段内都存在2 个共振峰，分别与模态分析中前2 个振动模态的频率相对应。由表3的对比可见，前2 个共振峰对应频率的仿真模型和实验测试结果间的相对偏差均小于2.3%，验证了本文所建立的考虑压电耦合效应的空间充气杆频率响应分析方法的有效性。仿真和实验获得的充气结构频率响应曲线在幅值上略有差异，可能是由于仿真中使用的经验阻尼参数与实际值不尽相同。

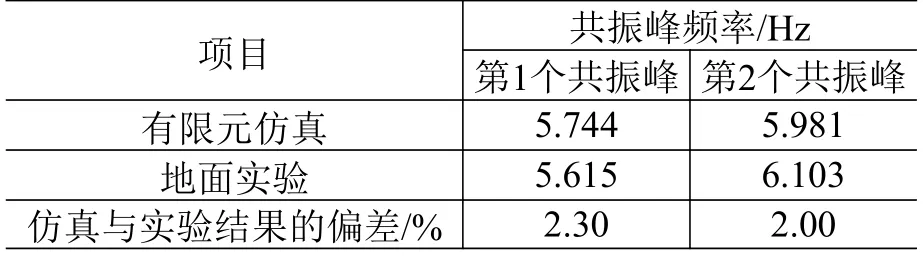
表3 仿真与实验共振峰频率对比Table 3 Comparison between simulated results and test results of resonant frequencies

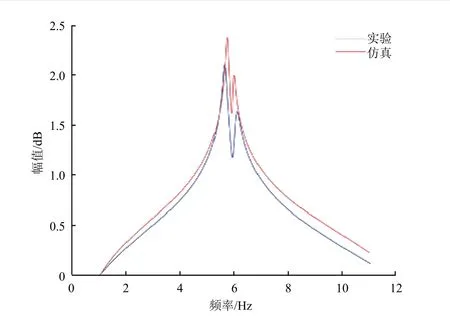
图10 空间充气杆频响曲线Fig. 10 Frequency response curve of the space inflatable rod

2.4 充气压力对频响特性的影响

对充气杆施加不同的充气压力将带来不同的预应力，对应不同的结构预应力刚度矩阵。为探究充气压力对空间充气结构频响特性的影响，运用本文所建立的充气结构频率响应分析方法分别对0.010 MPa、0.015 MPa、0.020 MPa、0.025 MPa 和0.030 MPa 共5 种充气压力下的充气杆进行频响特性仿真分析，得到其在不同充气压力下的频响曲线（见图11）和共振频率（见表4）。

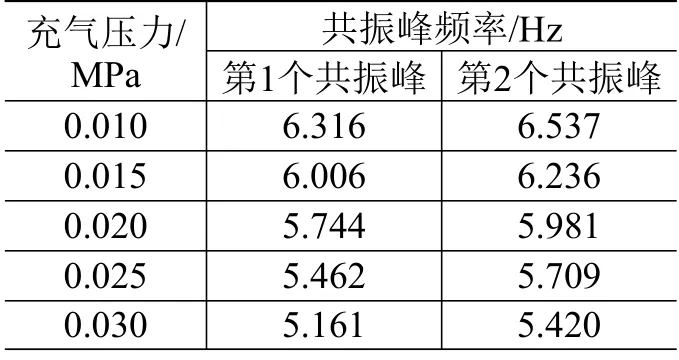
表4 不同充气压力下的结构共振频率Table 4 Resonance frequencies at different inflation pressures

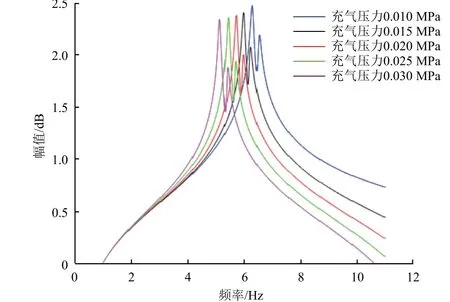
图11 不同充气压力下的结构频响曲线Fig. 11 Curves of frequency response under different inflation pressures

由上述结果可以看出，在一定充气压力范围内，充气压力和前2 个共振频率的变化呈负线性关系，随着充气压力的增大，空间充气杆的前2 个共振频率有降低的趋势，这是因为随着充气压力的增大，腔体内气体密度会增加，进而导致气体附加质量增加；当气体附加质量增加对结构刚度的影响超过充气压力增大所带来的影响时，将导致结构整体共振频率下降。因此，在结构的力学特性分析和优化设计时需要充分考虑充气压力的影响。

3 结束语

本文基于通用有限元软件ABAQUS，建立了考虑压电耦合的空间充气展开结构频率响应分析方法，依次进行非线性充气预应力分析、模态分析和频率响应特性分析，获得了考虑压电元件的空间充气杆的频率响应特性。同时，搭建了充气结构频率响应特性地面测试实验平台，利用MFC 压电激励和激光测振仪采集结构速度响应，获得了在相同充气压力下充气结构关心频段内的频响曲线。仿真分析与实验结果的对比验证了本文所提出的充气展开结构频响特性有限元仿真方法的有效性。使用验证后的仿真方法针对不同充气压力下的空间充气杆进行分析，结果表明充气压力对充气杆的频响特性有实质性影响。

本文研究结果可为进一步分析空间充气展开结构的动力学特性和实施结构优化设计提供参考。