基于两阶段特征选择和格拉姆角场的配电网拓扑辨识方法

潘毓笙，秦 超

（天津大学电气自动化与信息工程学院,天津市 300072）

0 引言

高比例分布式能源接入是未来配电网的基本特征。为应对分布式能源接入带来的不确定性,需要对配电网络进行频繁的拓扑重构,以保证配电网安全可靠经济运行［1-3］。配电网的拓扑信息是进行潮流计算、电压与无功优化、阻塞分析等工作的重要前提［4］。频繁变化的拓扑对配电网的管理提出了严峻挑战,如何准确高效地辨识配电网拓扑已成为亟须解决的关键问题。

近年来,国内外已有大量学者对配电网的拓扑辨识展开了研究,主要从2 种研究角度切入,分别是历史时序数据和时间断面数据。第1 种研究角度的基本思路是通过一段连续时间内配电网的时序量测数据,判断不同节点的连接关系,从而构建出网络拓扑。文献［5-8］通过分析不同节点电压间的相关性寻找节点连接关系。文献［9-11］以系统的潮流计算、状态估计功能为基础,对节点连接关系和线路参数进行联合辨识,但是要求大量且类型多样的量测数据。上述方法需要数小时的量测数据,无法实现配电网的在线拓扑辨识,若配电网拓扑在数据采样期间发生变化,则无法保证算法的有效性。

为了解决上述问题,一些研究从时间断面数据角度切入,通过建立配电网时间断面量测数据到拓扑的映射关系辨识其网络拓扑。文献［12］通过贝叶斯模型建立了光伏发电出力、负荷、节点电压幅值到配电网拓扑的映射关系。文献［13］通过深度置信网络建立了节点电压幅值到配电网所有开关状态的映射关系。但是,这些工作仅考虑了辐射状配电网,对于高比例分布式能源接入的配电网,需要考虑环状与辐射状拓扑混合运行的场景［14-15］。文献［16］通过深度神经网络直接拟合节点电压幅值与混合运行拓扑的映射关系,但是无法区分在部分系统运行状态下节点电压分布相似的拓扑,对量测存在误差的场景适应性较弱。

目前,受限于成本因素,量测设备在配电网中的配置不足。大多数研究［5-13,15］未能对时间断面的拓扑特征信息进行有效且充分的挖掘,一般需要全部量测的方式保证方法的有效性与适应性。

为此,本文提出一种基于两阶段特征选择和格拉姆角场（Gramian angular field,GAF）的配电网拓扑辨识方法。首先,基于XGBoost 计算每个量测的重要性,通过最大信息系数（maximal information coefficient,MIC）判定不同量测的相关性,从而筛选出重要且不冗余的量测数据。然后,基于GAF 特征变换,将一维时间断面的量测数据变换为二维的GAF,利用三卷积层神经网络模型实现准确、稳定的辨识拓扑。该方法仅需要部分节点电压幅值量测的时间断面数据,适用于分布式能源接入、辐射状拓扑和环网拓扑混合运行的配电网。

1 问题陈述

1.1 基本原理

目前,配电网拓扑辨识问题中最为常用的量测数据是节点电压幅值［5-8,12-13,16-17］。基于时间断面的节点电压幅值进行配电网拓扑辨识的原理如式（1）至式（3）所示。

式中:pi(t)、qi(t)和vi(t)分别为节点i在t时刻注入的有功功率、无功功率和电压幅值；h(∙)为潮流函数；N为配电网节点总数；εt为t时刻的拓扑辨识结果；C(t)为t时刻的节点电压分布；g(∙)为映射函数。

式（1）和式（2）表明,每个时间断面的C(t)由pi(t)、qi(t)和εt共同决定。式（3）表明,对于一个由时间断面的C(t)和相应的εt组成的数据集,通过给定C(t)的相似规律,可从数据集中匹配对应的ε(t),实现拓扑辨识［12-13,16-17］。

1.2 配电网电压分布特性

传统的中压配电网一般是辐射状拓扑,当不发生功率倒送或拓扑重构时,配电网的潮流是单向的,方向从电源流向负荷［18］,相应的配电网各条线路节点电压分布呈逐渐下降的趋势。

分布式能源接入后,配电网的节点电压分布变得更加复杂,可能引起馈线末端电压抬升等［19］。辐射状配电网闭合联络线形成弱环网,不同合环点因电压差的不同,会导致合环后对节点电压的提升作用不同,甚至可能出现抑制作用［20］。下面将通过具体场景来说明分布式能源接入对C(t)的影响。

同一拓扑下,考虑分布式能源随机波动性前后的节点电压分布特性如附录A 图A1 所示。不同拓扑下,考虑分布式能源随机波动性前后的节点电压分布特性如图A2 所示。可见,分布式能源随机波动性会导致同一拓扑下的电压分布特性更加多变,也可能导致不同拓扑下的电压分布特性呈现一定的相似性,增加准确拓扑辨识的难度。

此外,受到量测噪声的影响,节点电压分布会因为局部数值发生偏差［21］而发生改变。若量测数据出现缺失,则大量有用的拓扑特征信息可能会丢失［22］。

多种复杂因素使得配电网在不同拓扑下的电压分布规律更为隐蔽。因此,建立时间断面量测到配电网拓扑的准确映射变得十分困难。为了实现基于节点电压分布的相似规律辨识配电网拓扑,需要更为有效的数据挖掘方法提取在配电网电压分布曲线中隐藏的拓扑特征信息。

2 配电网在线拓扑辨识框架

本文提出了基于两阶段特征选择和GAF 的配电网拓扑辨识方法,其框架如附录A 图A3 所示。该辨识方法由离线和在线这2 个阶段组成。

1）离线阶段。首先,将不同拓扑结构下的节点电压幅值量测数据和相应的运行拓扑构成样本集。其次,对所有节点的量测数据进行特征选择,以筛选出不含冗余拓扑特征信息的量测数据。最后,将量测数据进行特征变换,即将一维的节点电压幅值量测时间断面数据转变为二维的GAF,传输至已设定的三卷积层神经网络模型中进行离线训练。

2）在线阶段。采集配电网当前时间断面的节点电压幅值量测数据,并进行特征变换,传输至训练好的拓扑辨识模型中辨识配电网当前的运行拓扑。其中,节点电压幅值量测数据可以通过数据采集与监 控（supervisory control and data acquisition,SCADA）系统、智能电表或相量测量单元（phasor measurement unit,PMU）获取。

2.1 两阶段特征选择

特征选择的目的是从配电网的全部量测数据中筛选出不含冗余拓扑特征信息的重要量测数据,指导配电网的量测优化配置。筛选出的量测数据应具备足够的拓扑信息,保证拓扑辨识的准确性。同时,量测数量应尽可能少,以适应配电网量测数据缺乏的实际。

XGBoost 是一种对梯度提升树（gradient boosting decision tree,GBDT）模型进行改进和优化的Boosting 集成学习算法,通过不断拟合上一棵树的残差来迭代产生新树,将所有树模型组成准确率更高、泛化能力更强的分类器［23］。此外,XGBoost还可以用于评价每个候选特征对于多分类问题的重要程度［23］。在本文中,拓扑辨识被处理为多分类问题,候选特征为节点电压幅值量测数据。因此,本文将XGBoost 用于判定每个节点电压量测对拓扑辨识问题的重要性,即通过决策树计算每个节点电压量测数据所有分裂子节点的信息增益。但是,依据重要度筛选出的量测数据可能包含大量冗余的拓扑特征信息。

MIC 是一种基于互信息和网格栅的关联评价方法,可以捕捉变量之间的联系并衡量相关关系［24］。其主要思想是,对于存在一定关联的2 个变量,在二维平面绘制这2 个变量的网格栅,通过每个网格栅计算相应的互信息值,将不同网格栅互信息的最大值作为MIC,常用于特征选择。本文将MIC用于衡量不同节点电压量测之间的相关程度,其优势是,对于相同噪声水平的2 个不同量测的相关关系,可以客观地给出相同或者相近的评价分数。但是MIC 无法对候选量测的重要性进行判断。

因此,本文提出一种基于XGBoost 和MIC 的两阶段特征选择方法,通过XGBoost 计算每个节点量测的重要性,基于MIC 判断不同量测间的相关关系,删除强相关且重要程度较低的量测数据,将剩余量测数据作为特征选择的结果。具体步骤如下:

步骤1:通过XGBoost 计算所有候选量测数据的重要度。

XGBoost 是由K棵决策树组成的加法集成模型［23］,如式（4）所示。

式中:SL、SR和SLR分别为叶子节点左决策子树、右决策子树和无分裂时式（6）的最优解,用于衡量叶子节点对总体损失的贡献；D为信息增益,当D<0时,表示决策树停止分裂。

遍历K棵决策树,将各量测数据作为分裂量测时得出的信息增益进行加权求和,作为该量测数据的重要程度。

步骤2:基于MIC 计算不同量测数据之间的相关关系［22］。

根据给定的网格栅,对vi和vj组成的二维空间进行划分,计算互信息值,表达式为:

由式（10）可知,当Ii,j,MIC>τ时,表示vi和vj强相关。其中,τ为强相关阈值。

步骤3:判断不同量测数据是否强相关,若2 个候选量测数据强相关,则删除重要程度较低的量测数据。

将量测数据按重要程度降序排序,将排序结果记为量测组合M。令β=N,α=N-1。

对M进行修正。对于M中第α个量测数据和第β个量测数据（α<β）,若二者强相关,则删除第β个 量 测 数 据,保 留 第α个 量 测 数 据,α减 去1；若α=0,则β减去1,α=β-1。重复执行,直至β=1结束,即排序结果中不再存在冗余量测数据。

2.2 特征变换

特征变换的目的是在不破坏原有的拓扑特征的同时,将量测数据中隐藏的拓扑特征信息提取并表征出来。常用的特征变换方法包括主成分分析（principal component analysis,PCA）、小 波 变 换（wavelet transform,WT）和GAF 等。PCA 的本质是降维,WT 的本质是对信号序列的分解和再重构,二者在进行特征变换的过程中,拓扑特征信息均存在一定程度的损失。

GAF 是一种可以将一维信号序列编码成二维图谱的特征变换方法［25］,包括格拉姆角求和场（Gramian summation angular field,GASF）和格拉姆角差分场（Gramian difference angular field,GADF）,一般用于图像分类问题。GAF 的本质是升维,能够充分挖掘样本中的拓扑特征信息,以保证拓扑辨识效果。因此,本文考虑采用GAF 进行特征变换,将一维的节点电压量测数据转换为图像,通过深度学习模型进行拓扑分类。GAF 不仅可以保留节点电压的分布规律,还可以提供节点之间的多种相对关系等其他拓扑特征信息,这对后续稳定提取拓扑特征工作起到重要作用。

通过GAF 进行特征变换的步骤如下:

步骤1:数值归一化。对每个时刻的节点电压量测数据进行归一化,表达式为:

若要同时包括GASF、GADF 中所表征的拓扑特征信息,只需保留GADF 的上三角元素和GASF的下三角元素。因此,本文结合GASF 和GADF,提出一种改进的GAF 二维表示,记为改进的GAF（Gramian angular field improved,GAFI）,如式（17）所示。

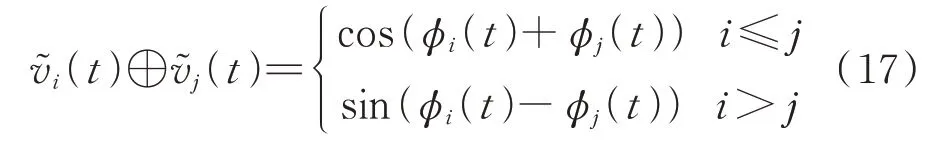
在GAFI 中,主对角元素通过余弦函数关系保留节点电压分布规律［25］,v͂i(t)和ϕi(t)的值可以通过余弦函数关系互相转换。上三角元素采用余弦函数表征相对关系［25］,由于余弦值在区间[0,π]内单调递减,表明不同节点的相对关系随ϕi(t)值的增大而减弱。下三角元素采用正弦函数表征相对关系［25］,由于正弦值在区间[-π/2,π/2]内单调递增,表明不同节点的相对关系随ϕi(t)值的增大而增强。

2.3 拓扑辨识

卷积神经网络（convolutional neural network,CNN）方法可有效提取图像的高维空间关键特征［26］。因此,本文采用CNN 方法来提取二维GAF的有效拓扑特征信息。具体步骤如下。

1）确定CNN 方法的基本结构

CNN 方法的输入为GAF,输出为拓扑标签。将单层卷积层、池化层和全链接层作为CNN 方法的基本结构。采用Adam 算法［24］自适应学习,加速模型收敛,默认学习率使用建议的0.001,神经元个数设置为16。采用ReLu 函数作为卷积层的激活函数,以增强模型的稀疏表示［26］,采用Dropout 函数提升模型的泛化能力［27］,采用Softmax 函数［27］将拓扑辨识结果输出。

2）模型的超参数确定

本文通过交叉验证的网格搜索法优化和确定CNN 方法的超参数。首先,确定各超参数取值范围,将各参数可能的离散取值进行排列组合,构建多个参数组合。其次,对于某个参数组合,采用6 折交叉验证方法评估模型性能,即将样本集随机分为6 等份,每个回合不重复地选择其中1 等份作为验证集,其余5 等份作为训练集,分别训练和验证CNN方法,并得到学习模型的性能分数,共6 个回合。然后,计算这6 个回合性能分数的平均值作为该参数组合的最终性能分数。最后,遍历所有参数组合,取学习模型分数最高的参数组合作为CNN 方法最优的超参数,如附录A 图A4 所示。图中:卷积核尺寸为3,个数为32。3 次卷积和池化操作有效弱化了工程范围内噪声数据的影响,并高度抽象了拓扑特征信息。

3 算例分析

本文以改进的IEEE 33 节点系统验证所提方法的有效性。该系统的初始拓扑如附录A 图A5 所示,线路参数可参考文献［28］。在该系统中,分别接入2 组风电机组和2 组光伏发电单元,接入位置和具体容量参考文献［29］。使用Matpower 软件仿真获得所有节点的电压量测数据［30］。假设光伏发电单元和风机机组的出力曲线服从高斯分布,均值为每一时刻的实际出力,方差为实际出力的10%。假设负荷出力曲线也满足高斯分布,均值为每一时刻的实际出力,方差设为实际出力的5%,负荷功率因数服从均匀分布U(0.75,0.85),其中,U(∙)为平均分布函数。假设风机能够维持机端电压恒定,将接入风机的节点设置为有功功率-电压（PV）节点,将接入光伏的节点设置为有功功率-无功功率（PQ）节点。

3.1 有效性验证

3.1.1 样本生成

以附录A 图A5 所示的初始拓扑为基准,通过以下步骤生成典型拓扑构成待辨识的拓扑库:

步骤1:闭合任一或多个联络开关的同时,断开相同数量的线路开关。

步骤2:直接闭合任一或多个联络开关。

形成的拓扑库中包括213 种辐射状结构和94 种环状结构,样本总数为240 574。每个样本添加0.01%的零均值高斯噪声［31］。数据缺失的模式参考文献［32］,数据缺失比例设置为5%,使用K近邻（Knearest neighbor,KNN）方法填补缺失值［33］。训练集、验证集、测试集数量的比例为8∶1∶1。采用精确率和召回率的调和平均值F1来评估拓扑辨识模型性能,计算公式如附录A 式（A1）至式（A3）所示。

3.1.2 特征选择方法验证

采用XGBoost 计算量测数据的重要性,量测数据按重要程度降序排序结果如图1 所示。不同量测数据之间的相关关系热图如附录A 图A6 所示。对量测组合进行修正,GAF-CNN 方法测试集的F1与τ的关系如图A7 所示。随着强相关阈值的增加,特征选择后所保留的量测数据个数也就越多。若采用全部特征进行训练,测试集的F1值为99.03%。当τ≥0.7 时,F1趋 于 稳 定；当τ<0.7 时,F1开 始 大 幅度下降。可见,当τ=0.7 时,所筛选的量测组合为{V25,V18,V1,V22,V14,V33,V10,V7,V5,V29}已不含冗余拓扑特征信息,量测个数为10,测试集的F1值为97.16%。若未对量测组合进行修正,直接选用降序排 序 结 果 中 前 10 的 量 测 组 合 为{V25,V18,V1,V22,V14,V33,V10,V12,V9,V7},测试集的F1为95.29%。其 中,V14与V12、V10与V9为 强 相关关系。这意味着,当配电网量测数据不足时,不含冗余拓扑特征信息的量测配置,要比直接选用XGBoost 降序结果中前10 位的量测数据更有效。

图1 量测重要程度降序排序结果Fig.1 Sorting results in descending order of importance of measurements

3.1.3 GAF-CNN 方法验证

为了验证GAF-CNN 方法的有效性,选择支持向量机（support vector machine,SVM）、深度神经网络（deep neural network,DNN）、CNN 等常用方法作为对照。

不同方法的拓扑辨识结果如表1 所示。表1 表明,在未进行特征变换之前,CNN 方法的F1最高,为85.63%。DNN 方法的F1比CNN 方法小4.85%,SVM 方法的F1比CNN 方法小13.07 个百分点。在进行特征变换之后,GASF-CNN 方法、GADF-CNN方法和GAFI-CNN 方法的F1分别为94.64%、95.01%、97.16%,相较于不采用特征变换的CNN方法分别提升了9.01、9.38、11.53 个百分点,表明GASF、GADF、GAFI 均能显著提升CNN 方法的拓扑辨识性能,其中本文建立的GAFI 效果更为明显。

表1 不同方法的拓扑辨识结果Table 1 Topology identification results with different methods

3.1.4 可视化解释

为了直观说明GAF 的有效性,本文将CNN 方法未能准确辨识的部分样本以热图形式描述,如附录A 图A8 所示。可以看出,GAF 可显式地表达拓扑之间的差异与共性。通过可视化工具t-SNE［34］将CNN 方法与GAFI-CNN 方法的最后一层输出映射到二维平面上,可视化结果如图2 所示。图中:横纵坐标代表空间距离,每一个样本映射为二维平面的一个点,点与点之间的距离表示样本间的相似度。相似度高的点紧密聚合,相似度低的点距离疏远。每个点根据CNN 方法所拟合的映射关系,聚合成不同的簇。图2 表明,与CNN 方法相比,GAFI-CNN方法的最后一层输出存在更多的簇,簇间的层次更为分明。可见,GAF 能够给CNN 方法提供更为明确的拓扑特征信息,包括节点电压分布规律和节点之间隐藏的相对关系等。这些拓扑特征信息帮助CNN 方法建立时间断面量测到拓扑的准确映射关系。

图2 CNN 方法最后一层输出的可视化结果Fig.2 Visualization results of last-layer outputs of CNN methods

3.2 适应性分析

本节采用的节点量测组合为{V25,V18,V1,V22,V14,V33,V10,V7,V5,V29},进一步检验所提方法对于不同量测噪声水平、不同数据缺失比例以及其他场景的适应性。

3.2.1 不同噪声水平

为了评估所提方法对不同量测噪声水平的适应性,本节在5 组不同程度的零均值高斯噪声的样本集进行测试,噪声的方差分别为0.01%、0.02%、0.03%、0.04%、0.05%,其余边界条件与3.1.1 节保持一致。

不同量测噪声水平对所提方法的影响如图3 所示。图3 表明,随着噪声水平的增加,GAF-CNN 方法的F1出现了不同程度的下降。但是,在最高0.05% 的量测噪声水平下,F1仍可以维持在92%以上。

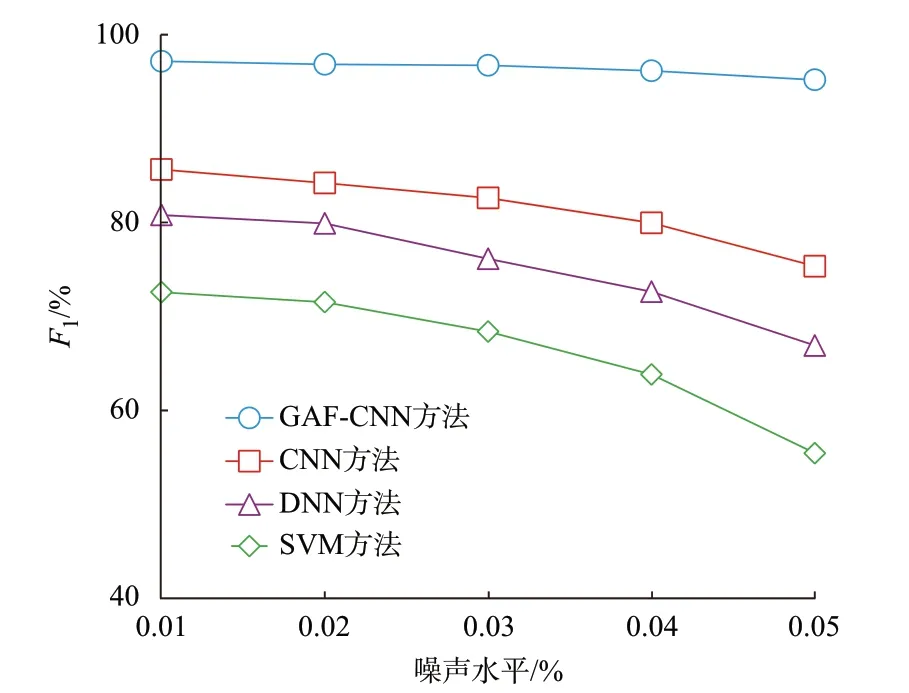
图3 不同量测噪声水平对所提方法的影响Fig.3 Influence of different noise levels on proposed method

量测数据的非同步性同样会影响拓扑辨识的准确性,体现为对真实值的偏移,即量测噪声。本文考虑了多种量测噪声的情况,能在一定程度上反映数据非同步性带来的影响。本文的主要研究对象是中压配电网,其地理分布范围较小,量测数据的非同步问题不突出。

3.2.2 不同数据缺失比例

为了评估所提方法对不同数据缺失比例的适应性,本节在5 组不同数据缺失情况的样本集进行测试,数据缺失的比例分别为5%、10%、15%、20%、25%,其余边界条件与3.1.1 节保持一致。

不同数据缺失比例的影响如附录A 图A9 所示。由图可知,随着数据缺失比例的增加,GAFCNN 方法的F1出现不同幅度的下降。但是在最高25%的数据缺失比例下,F1仍可以维持在95%以上,而CNN 方法的F1已下降至75.34%。

3.2.3 其他场景适应性

本文选择文献［12-13］和文献［16］所提的5 种场景,边界条件如附录A 表A1 所示。辨识结果的比较如表A2 所示。在场景1 中,所提方法的F1可达99.34%,在场景2 和场景5 中,所提方法的F1分别为99.62%和99.72%。这意味着,输入仅包含节点电压幅值量测可保证拓扑辨识性能,其他量测数据对最终性能提升有限。在场景3 和场景4 中,所提方法的F1超过98%。这表明,所提方法在其他场景下具备良好的适应性。

4 结语

本文提出一种基于两阶段特征选择和GAF 的配电网拓扑辨识方法。通过算例分析,得到如下结论:

1）所提方法基于XGBoost 计算量测数据重要性,通过MICE 判定不同量测数据的相关性,可以指导筛选不含冗余拓扑特征信息的重要量测组合,能够给配电网配置量测数据提供更为合适的参考。

2）所提方法将一维的节点电压幅值时间断面量测数据变换为二维的GAF,结合三卷积层的神经网络模型,可实现配电网在线拓扑辨识。

3）改 进 的GAF 二 维 表 示GAFI,与GASF 和GADF 相比,更能够表征时间断面中所蕴含的丰富的拓扑特征信息,显著提升CNN 方法的辨识效果。

4）所提方法在不同噪声水平、数据缺失比例以及其他场景下均具备良好的适应性。

后续研究将考虑分布式电源接入的配电网进行拓扑和线路参数的联合辨识。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。