黄河下游“驼峰”河段来水来沙条件和不平衡输沙特性研究

黄飞扬, 周子骏

(1.河海大学 水利水电学院， 江苏 南京 210024； 2.南京水利科学研究院， 江苏 南京 210024)

1 研究背景

由于黄河下游水流含沙量较大、水沙年际间不平衡以及独特的地理环境[1-3]，使其逐渐成为了典型的不平衡输沙河段[4]，在这种情况下河流发展十分迅速，河床演变剧烈，尤其在高村-艾山河段表现得尤为明显，出现了过洪水能力远小于其上、下游河段的“驼峰”现象[5]，因而高村-艾山河段为小浪底水库运用后黄河下游河道整治的重点区域。为了对此现象进行合理解释，众多学者对驼峰河段的特殊性进行了研究，其中，钱宁[6]采用上站含沙量获得了计算黄河下游各河段的输沙率公式，此公式结构简单、方便实用，在黄河下游的河道输沙计算中得到了广泛的应用；韩其为[7]在前人研究的基础上对黄河下游驼峰河段的成因进行分析，探索了黄河下游不平衡输沙现象的发展过程；陈绪坚等[8]通过改进黄河下游泥沙配置综合评价方法，计算出了改善河道不平衡输沙危害的新水沙系列和配置模式条件；张旭东等[9]在上述学者研究的基础上，采用空间插值和实测资料分析了下游河段的地貌演变情况，并提出了“驼峰”河段的整治方案。江恩惠等[10]总结出了黄河下游不平衡输沙的两大问题，并对黄河下游驼峰河段的特殊性机理给出了合理解释。上述研究成果表明，黄河下游不平衡输沙特性是驼峰现象发展的诱因，该问题亟待解决。

目前研究不平衡输沙的方法主要是拟合输沙率经验公式[11-12]和分析排沙比与来水来沙关系[13-14]的影响因素。如钱宁等[15-16]对黄河下游河道输沙能力进行了全面的分析，从而提出了满足黄河下游输沙特点的经验公式，进一步建立了河段输沙率与不平衡输沙之间的关系，但其研究中没有完全给出各个参数与河道水沙特征、地貌特征之间的相关性和趋势性，然而在对黄河下游河道输沙自我调整能力进行分析后可以发现，黄河下游的输沙率与上游流量、含沙量均存在一定的关系[17]。在对驼峰现象的研究过程中，众多学者都对其形成机理给出了解释，并对其发展趋势进行了预测，陈建国等[18]针对河段断面形态特征，分析了“驼峰”河段的形成原因，并提出了“机械挖淤”的治理方式；齐璞[19]提出了塑造窄深河槽的方法来改造“驼峰”河段，利用窄深河道可提高输沙率的特点，将高含沙水流输送入海，以改善驼峰现象；许炯心[20]分析多个洪水场次的资料后，计算得出了黄河下游各河段“微冲不淤”的临界来沙系数，提出了改善黄河下游驼峰河段的流量与含沙量范围。对于黄河下游河段，采取一定的措施塑造合理的水沙过程，对于“驼峰”河段的治理具有重要的意义。因此本文在钱宁等[15-16]总结的黄河下游河道输沙率公式的基础上进行推导，进一步拟合出了黄河下游河段排沙比分别与来水来沙条件、断面形态特征之间的计算公式，同时建立了完整的黄河下游泥沙输移体系与黄河下游来水来沙条件、河道断面形态特征之间的函数关系，使黄河下游不平衡输沙理论得到进一步的完善。

2 黄河下游来水来沙量变化过程分析

黄河下游河道承担着泄洪及泥沙输送的双重任务，来水来沙条件受小浪底水库调节作用的影响。通过花园口水文站实测水文数据对黄河下游“驼峰”河段发展较为明显的1990-2020年的黄河来水来沙过程进行统计，得到的来水来沙量变化过程如图1所示。

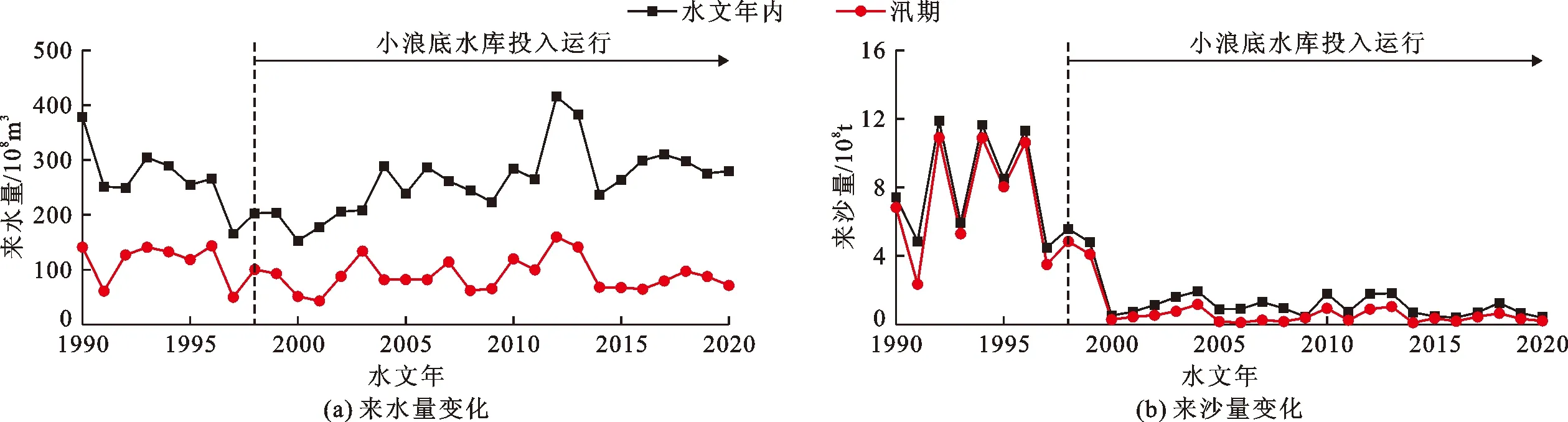
图1 1990-2020年黄河下游花园口水文站各年份来水来沙量变化情况

如图1所示，在1998年之前，即小浪底水库建成投入使用之前，花园口站来水量连续偏枯，来沙量年际变化较大，年内水沙分配不均衡，其中最小来沙量年份为1997年，仅为4.5×108t，最大来沙量年份为1992年，高达11.8×108t。当1998 年小浪底水库正式投入运行之后，水库自身对黄河下游年内水量起到了“丰蓄枯排”的调节作用，使得年内水量分配发生变化，其中汛期水量逐渐减小且变化平稳；在小浪底水库的拦蓄作用下，大量泥沙沉积在小浪底库底，使其下游水流含沙量急剧减小，年均来沙量由1998年小浪底水库运行之前的5.80×108t/a减少到2020年的0.65×108t/a，减少了88.7%。

有关资料文献[16]表明，黄河下游的冲淤变化主要发生在含沙量变化较大的汛期，汛期的下游河道主要承担着水量输送和泥沙输运的任务，这使得黄河下游在汛期会产生较为剧烈的河道演变。通过对1990-2020年黄河下游高村-艾山河段的汛期和非汛期的来水来沙量数据进行统计后发现，相对于非汛期而言，各年份汛期的来水来沙过程相差较大。1990-2020年汛期和非汛期黄河下游高村-艾山河段冲淤量年际变化以及高村水文站来沙系数如图2所示。

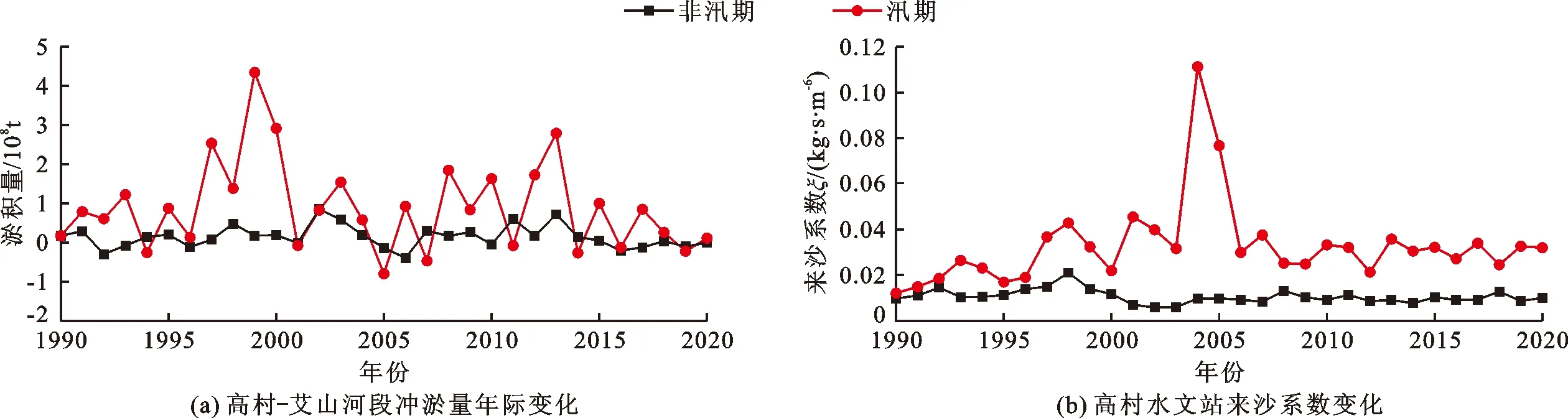
图2 1990-2020年汛期和非汛期黄河下游高村-艾山河段冲淤年际变化及高村水文站来沙系数

如图2所示，1990-2020年汛期黄河下游高村-艾山河段不同年份的淤积量变化较大，有些年份还发生了冲刷，而非汛期河道整体基本保持冲淤平衡状态(图2 (a))。相应时段黄河下游高村水文站汛期的来沙系数明显大于年内非汛期的来沙系数(图2 (b))，从侧面反映出黄河下游在汛期存在“水少沙多，水沙搭配不平衡”等问题。黄河下游高村站非汛期来沙系数各年份基本维持在0.009 8 kg·s/m6左右，且在非汛期黄河下游高村-艾山河段总体淤积量略小于0，表明黄河下游“驼峰”河段在非汛期保持着较好的“微冲不淤”状态；但汛期由于水沙关系不协调，黄河下游“驼峰”河段主要以淤积为主，此时黄河下游高村-艾山河段整体表现为“多来多排多淤”的状态。

3 黄河下游汛期不同量级流量下的输沙关系分析

由图2、3可知，黄河下游在汛期会产生较强的河道冲淤变化，而在非汛期河道基本维持“微冲不淤”的状态。所以对黄河下游1990-2020年各年份的汛期水文资料进行了重点研究，发现当各水文站点的水流含沙量小于25 kg/m3时，黄河下游在小浪底水库的调节下长期处于较为稳定的冲刷状态；而当黄河下游各水文站点的水流含沙量达到25～65 kg/m3时，由于受到上游来水量和地形地貌的影响，黄河下游各河段的冲淤状态较为复杂；若各水文站点的水流含沙量大于65 kg/m3时，在现有的黄河水文资料记载中，下游河道一直处于淤积状态。

为了进一步了解汛期不同流量条件下黄河下游河段水流含沙量和冲淤比(冲淤比定义为冲淤量与来沙量之比，用于描述河道冲淤效果)之间的关系，对较为复杂的流量变化序列进行分级研究，其中将黄河下游流量按大小分为1 000～2 000、2 000～3 000、3 000～4 000、4 000～5 000 m3/s共4级，并分析不同流量级情况下含沙量变化对黄河下游河道冲淤比的影响，其结果如图3所示。

图3中各级流量含沙量与冲淤比之间的关系均以Log3P1型曲线进行拟合，其拟合方程形式为y=a-b·ln(x+c)，具体拟合结果见表1。

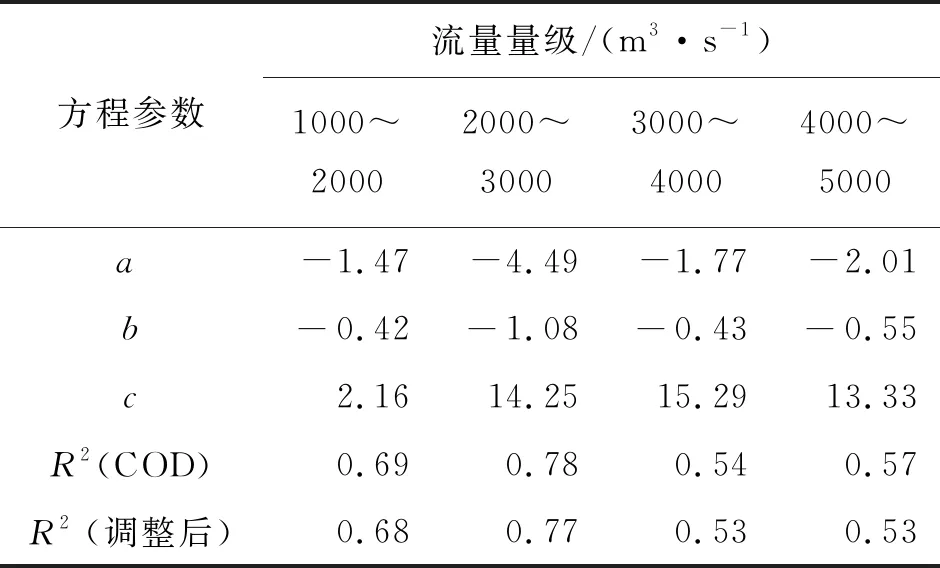
表1 各级流量含沙量与冲淤比关系曲线拟合结果

由图3和表1可知，不同流量量级下黄河下游河段水流含沙量与冲淤比呈较为明显的正比关系，且二者关系较为符合对数函数。随着含沙量的增大，黄河下游淤积效果明显增强，当含沙量逐渐增大到50 kg/m3以上时，冲淤比在不同流量量级条件下均大于0，黄河下游处于一种持续淤积的状态。

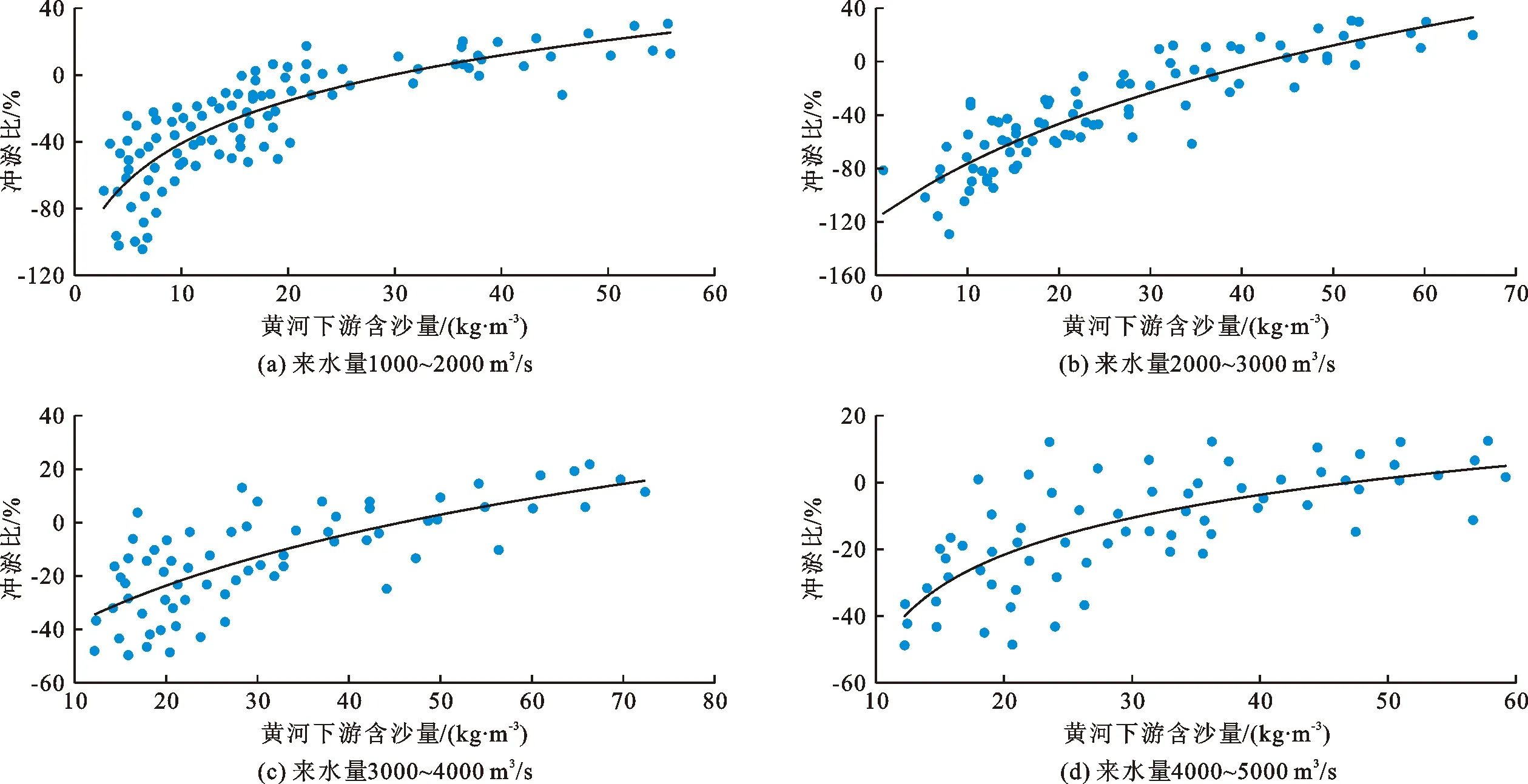
图3 不同流量级下黄河下游河段水流含沙量与冲淤比之间的关系

综合上述分析可知，在不同来水量和含沙量组合条件下黄河下游河段的冲淤特性存在较大的差异。为了进一步研究黄河下游来水来沙条件与淤积量之间的关系，可利用黄河下游全河段排沙比λs(排沙比λs为一定时段出口沙量与进口沙量之比)估算一定水沙条件下黄河下游的淤积量Ws。黄河下游全断面的河道淤积量公式如下：

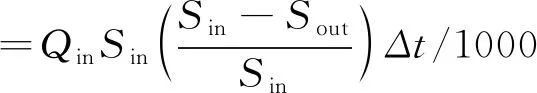
=QinSin(1-λs)Δt/1000

(1)

式中：Ws为黄河下游全断面的淤积量，t；Qin为花园口水文站测点的进入流量，m3/s；Sin、Sout分别为花园口水文站测点进口、出口的水流含沙量，kg/m3；λs为黄河下游全河段排沙比，通过查阅相关时间段的黄河下游水文年鉴获取；Δt为时间段，s。

可以将1 d(即Δt=86 400 s)的淤积量定义为黄河下游河段的淤积强度Ws/d，用于分析每日来水来沙条件对河道冲刷的影响。Ws/d的计算公式如下：

Ws/d=86.4QinSin(1-λs)

(2)

式中：Ws/d为黄河下游全断面的淤积强度，t/d。

利用公式(2)和1990-2020 年黄河下游水文资料对黄河下游汛期非漫滩流量进行统计计算，得到了如图4所示的黄河下游来水来沙条件与河道淤积强度关系云图(图中无实测点的淤积强度定义为0)。

图4 黄河下游全断面来水来沙条件与河道淤积强度的关系云图

以黄河下游实际汛期流量范围为参考值，当黄河下游河段来水来沙量在图4所示的矩形区域中时，则黄河下游的淤积强度在年内的平均值处于“微冲”状态，结合图3所示的4个不同流量级和含沙量组合的冲淤比变化结果总结得出：当花园口进口流量为3 000～4 300 m3/s、含沙量为35.0～42.5 kg/m3时，淤积强度平均值在0附近，此时黄河下游可保持较为稳定的均衡输沙方式。

4 黄河下游“驼峰”河段排沙比与来水来沙条件之间的关系

为了进一步探讨黄河下游“驼峰”河段独特的水沙特性，需要对黄河下游河段的来水来沙情况与排沙比之间的关系进行分析，通过参考相关研究发现黄河下游排沙比可能直接受到黄河下游河道之间泥沙级配的影响。在对黄河下游相关流速查询中，因无法准确地计算出黄河下游的纵比降，从而不能通过求得河道摩阻流速而推算出不同流量级下泥沙浓度对应的输沙率。所以本文使用黄河下游来水来沙时间序列作为本次计算的基本条件，建立1990-2020年黄河下游“驼峰”河段排沙比λs与来水来沙条件之间的关系，引入来沙系数ξ作为重要参数，用于表征水沙条件(来沙系数定义为含沙量S与流量Q之比)。其中排沙比λs可以表示为：

(3)

式中：λs为排沙比；Qs-in、Qs-out分别为河段进口、出口的输沙率，kg/s；Δt为计算时间段。

由于黄河下游为典型的不平衡输沙河段，可以采用钱宁等[15-16]论证的黄河下游河段输沙率经验公式对黄河下游输沙率进行计算，黄河下游不平衡输沙率经验公式可以表示为：

(4)

式中：K为输沙系数，其值随着河床的冲刷量的增大而减小；a为沙量指数，与河床纵比降呈正相关；b为流量指数，与河道的河相系数呈负相关。经钱宁等[15]验证发现a+b=2，其中a<1且b>1。

由于黄河各河段进、出口距离较远，使得出口输沙量对于黄河下游各河段的输沙率影响逐渐减小，此时可以认为沙量指数a→0，再将公式(4)代入公式(3)可得：

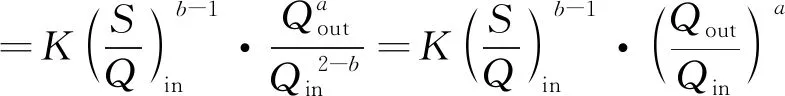
(5)

在不考虑人为因素和水文条件(如降雨、蒸发、下渗[13]、入汇流[21])等因素的影响时，可以认为流量Qin=Qout，从而简化公式(5)可以得到：

λs=Kξb-1

(6)

根据公式(6)可知，黄河下游各河段的排沙比与来沙系数呈幂指数函数关系，为了验证“驼峰”河段(高村-艾山河段)因其独特的地形环境和水沙关系，而导致其河道输沙条件和输沙关系与其他河道存在的较大差异，对黄河下游花园口-高村、高村-艾山河段的排沙比与来水来沙条件建立幂函数关系，拟合结果如图5所示。

图5 黄河下游花园口-高村、高村-艾山河段排沙比与来水来沙条件之间的幂函数关系

如图5所示，黄河下游“驼峰”河段及其以上河段排沙比与来沙系数之间存在较强的关联性，对上述二者关系进行幂函数拟合，拟合得到的相关参数如表2所示。

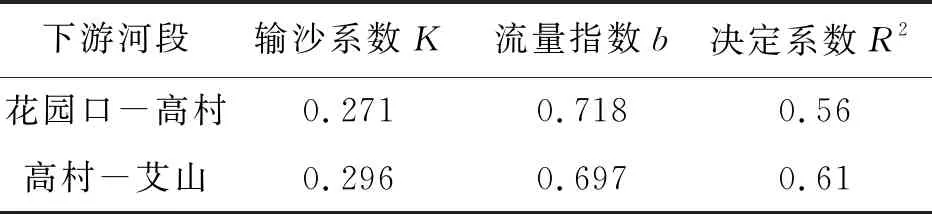
表2 黄河下游花园口-高村、高村-艾山河段排沙比与来沙系数幂指数关系拟合结果

如表2所示，黄河下游花园口-高村、高村-艾山河段排沙比与来沙系数之间存在较好的关联性和趋势性，二者拟合的幂指数函数曲线的决定系数分别为0.56和0.61。比较表2中的相关参数可以发现，花园口-高村河段的输沙系数K较高村-艾山河段偏小，表明花园口-高村河段相比于高村-艾山河段的冲刷量较大；花园口-高村河段的流量指数b较高村-艾山河段偏大，表明花园口-高村河段的河相系数较小，河道相对窄深，高村-艾山河段的河相系数较大，河道相对宽浅。当排沙比λs=1时(当λs>1时，河流处于冲刷状态；当λs<1时，河流处于淤积状态)，即河道处于冲淤平衡状态时，花园口-高村河段相应的来沙系数为0.012 kg·s/m6，而下游的高村-艾山“驼峰”河段达到冲淤平衡时，其相应的来沙系数为0.010 kg·s/m6，这也间接表明了在相同的水沙情况下，“驼峰”河段对于泥沙具有较强的滞留性。从而证明了黄河下游各河段之间仍处于一种不平衡发展阶段。对图5中来沙系数的区间进行对比后可以发现，花园口-高村河段的来沙系数相较于高村-艾山河段偏小，在这种情况下使得高村站以下河段处于非饱和的输沙状态，从而十分有利于高村站下游输沙，减小了下游“驼峰”河段的淤积量。

5 黄河下游河槽形态特征与排沙比之间的关系

黄河下游河道尤其是花园口-高村游荡性河段的断面十分复杂[22]，为典型的复式断面，由于黄河下游河段河型存在差异，其输沙方式也有较大的不同。因此为了考虑河道断面形态对于黄河下游水沙关系的影响，在以往的研究中一般需要引入河相系数来表示断面的形态。早期的河相关系基本上是经验性质的，本文选用较为经典的格鲁什科夫的河相系数计算公式[22-23]，其表达式如下：

(7)

(8)

由公式(8)计算得到的黄河下游花园口-高村、高村-艾山河段的平滩河槽形态参数如图6所示。由图6可以看出，黄河下游河段的平滩水深呈不断增加的趋势，且花园口-高村河段相较于高村-艾山河段的增幅更大，尤其是1999-2002 年小浪底水库投入使用后，使得黄河下游游荡性河段在年内整体以冲刷为主，从而造成河道加深。在河段平滩河宽方面，由于花园口-高村河段为典型游荡性河段，河床稳定性较差，所以河宽年际变化较为剧烈，但其平均值基本稳定。

根据花园口-艾山河段的地形资料[24]和图6的计算结果，采用公式(7)对黄河下游达到平滩流量时的河相系数进行计算，并对1990-2020 年黄河下游的实测水沙资料进行统计，由此计算出黄河下游花园口-高村、高村-艾山河段的排沙比与河相系数之间的变化关系，结果如图7所示。

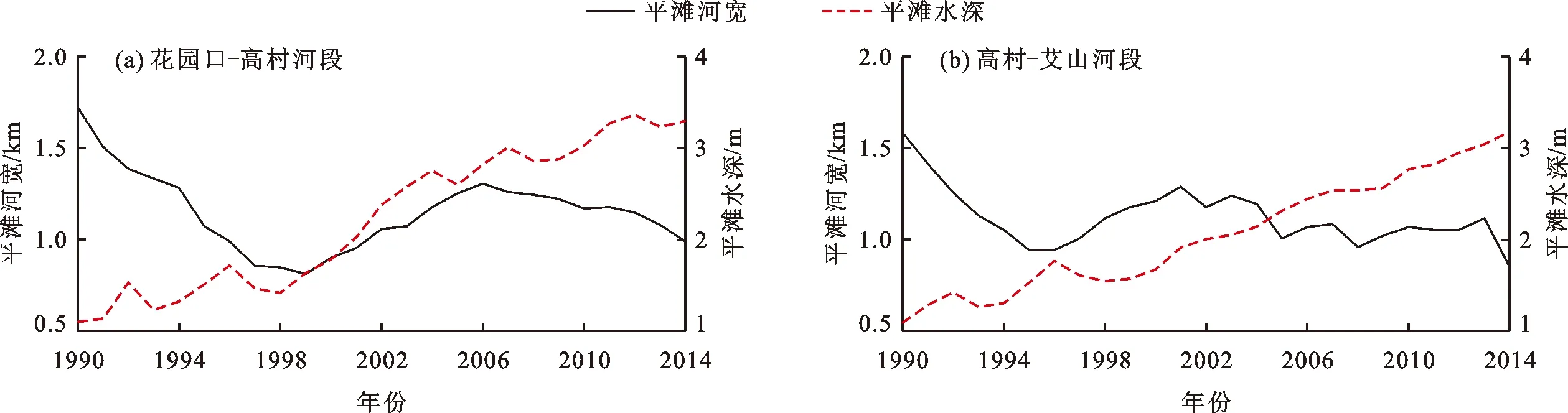
图6 黄河下游花园口-高村、高村-艾山河段平滩河槽形态参数

图7 黄河下游花园口-高村、高村-艾山河段河相系数和排沙比之间的变化关系

如图7所示，黄河下游游荡性河段(花园口-高村河段)和“驼峰”河段(高村-艾山河段)的排沙比λs与河相系数ζ之间存在较为稳定的幂函数关系，拟合公式的决定系数R2分别为0.53和0.47，表明公式的相关性较好。当河相系数逐渐增大时，排沙比逐渐减小，这是因为随着河相系数的增大，河道变得宽浅，使得河道输沙能力逐渐减弱。从河相系数的分布上看，花园口-高村河段由于河床的不稳定性导致河相系数范围分布较广，当河相系数ζ大于26 m-1/2时，该河段处于淤积状态；高村-艾山河段的河相系数分布范围较窄，河道相对较为稳定，当河相系数ζ大于9 m-1/2时，该河段处于淤积状态。这也证明在相同的河道断面形态情况下黄河下游“驼峰”河段更加容易淤积。总体上看，上述河段在不同的年份内有淤有冲，但“驼峰”河段冲刷难度较大，更易淤积。

通过以上分析可知，黄河下游排沙比与来沙系数ξ、河相系数ζ之间均保持着较好的幂函数关系，故可以建立黄河下游河段来水来沙条件与河槽形态的特征函数，同时考虑两者对黄河下游河道冲淤特点的影响，最终建立的函数表达式如下：

λs=K1ξA-K2ζB+C

(9)

式中：K1、K2分别为沙量输沙系数和形态输沙系数；A、B分别为沙量指数和形态指数；C为经验参数，主要受到河流比降、河道糙率等因素影响。

本文对黄河下游水文年鉴1990-2020年中各水文站点的数据进行了统计，并结合公式(9)对其中的参数K1、K2、A、B、C进行了计算。再对水文年鉴数据进行了相关性分析，对参数的正确性进行了率定和验证。得到如表3所示的率定结果。

表3 黄河下游花园口-高村、高村-艾山河段公式(9)参数率定结果

如表3所示，黄河下游花园口-高村、高村-艾山河段公式(9)拟合曲线的决定系数R2分别为0.68和0.73，相较于公式(6)的相关性有所提高；对公式(9)右边各项参数的数值大小进行对比后发现，K1ξA小于K2ζB且前者仅为后者的50%，说明来沙系数相较于河相系数对排沙比的影响更弱，即来沙系数对河道冲淤情况的影响小于河流断面形态的影响；公式(9)中加入了经验参数C，可以更加全面地反映出黄河下游不同河型对河道冲淤变化的作用，因此公式(9)可以更加准确地计算出黄河下游河段排沙比与来沙系数、河流断面形态之间的关系。

6 结 论

本文利用黄河下游河段1990-2020年实测的水文资料，对黄河下游来水来沙条件进行了分析。以“驼峰”河段特殊的不平衡输沙特点为基础，建立了黄河下游排沙比与来沙系数、断面形态之间的函数关系，得出如下结论：

(1)自1998年小浪底水库投入使用后，黄河下游来水来沙量急剧减少。黄河下游汛期河道总体处于淤积状态；非汛期来沙系数维持在0.009 8 kg·s/m6左右，黄河下游总体上维持着“微冲不淤”的稳定状态。

(2)通过对黄河下游汛期水沙关系进行分析并对来水流量进行分级，研究了汛期不同流量情况下冲淤比与黄河下游含沙量之间的关系。结果表明，当黄河下游花园口进口流量在3 000～4 300 m3/s、含沙量在35.0～42.5 kg/m3区间时，黄河下游可保持较为稳定的均衡输沙模式。

(3)黄河下游驼峰河段相较于其上游河段更易于淤积，“驼峰”河段冲淤平衡的来沙系数为0.010 kg·s/m6，与结论(1)所示的黄河下游来沙系数维持在0.009 8 kg·s/m6时河道处于“微冲不淤”的状态进行对比，“驼峰”河段易于淤积且年内长期处于淤积状态。

(4)使用黄河下游地形实测资料和水文资料构建了河槽形态特征与排沙比之间的幂指数关系。进一步建立了如公式(9)所示的黄河下游河段排沙比的计算公式，该公式相较于公式(6)提高了计算的准确性，更适合于对黄河下游不平衡输沙率的计算。