基于组合赋权法和Vague集理论的预警卫星探测效能评估
陈秋琼,洪 俊,徐华志,2
(1.海军大连舰艇学院信息系统系,辽宁 大连 116018;2.中国人民解放军91889部队,广东 湛江 524000)
0 引言
预警卫星用于监视、发现和跟踪敌方战略导弹,是导弹防御系统中的重要节点,科学合理地评估预警卫星探测效能,对于导弹防御系统效能的整体评估具有重要指导意义。目前关于侦察卫星效能评估方法的研究并不全面。文献[1]建立了光学侦察卫星效能指标评估体系,通过仿真分析对比不同方案的优劣性;文献[2]针对多任务预警时效能评估能力不足的问题,提出了一种基于模糊综合法的效能评估方法;文献[3]在构建预警卫星情报处理系统效能指标体系的基础上,依靠专家对系统各指标进行打分从而评估系统整体效能;文献[4]从预警卫星工作模式角度,建立了海量情报处理系统评估体系和数学模型。以上系统效能评估方法在评价过程中,指标权重主要是通过主观赋权的方法给定,缺乏数学定量评价,不能完全排除人为因素带来的误差,很难真实反应待评估系统效能的优劣程度。
针对上述问题,本文提出一种基于组合赋权法和Vague集理论的预警卫星探测效能评估方法。该方法在建立科学的评估指标体系基础上,将区间层次分析法和改进CRITIC法综合确定指标组合权重,使指标权重的计量更加科学合理;构造Vague集决策矩阵,利用Vague集综合决策规则评估单一系统效能的优劣。
1 评估指标体系
1.1 指标体系构建
影响预警卫星系统探测效能的因素很多,各因素间存在一定的关联性,因此指标权重的分配需科学合理。结合预警卫星系统的工作特点,依据指标体系构建原则对预警卫星系统进行指标体系构建。预警卫星系统的探测效能主要从探测能力、识别能力、跟踪定位能力、预报能力四个方面体现[5]。本文建立的预警卫星系统效能评估指标体系如图1所示。
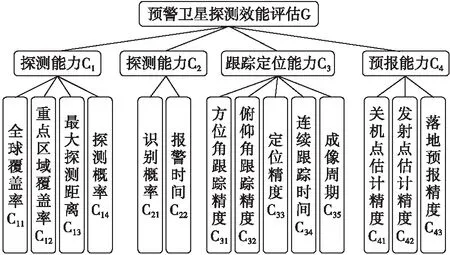
图1 预警卫星系统评估指标体系Fig.1 Evaluation index system of early warning satellite system
1.2 指标权重求解
预警卫星系统指标权重的确定需要根据系统作战流程和特点综合考虑影响系统效能的主观和客观因素。效能指标权重的求解主要有主观赋权法和客观赋权法两类。主观赋权法通过专家打分评估指标的重要性,优点是直观性强,但受人为影响因素较大;客观赋权法通过客观数据分析处理,操作简便,但过于依赖数据,完全忽略了专家意见,也存在一定的局限。将主、客观赋权法相结合确定最终指标权重,能够对结果进行有效修正。
本文采用区间层次分析法(IAHP)和改进CRITIC法对系统指标进行组合赋权,有效解决了传统层次分析法难以精准评测和传统CRITIC法在赋权过程中容易出现指标差异性和冲突性的问题;同时,通过采用博弈论极化模型计算组合权重既降低了评估者的主观偏好又反映了客观数据的影响。
1.2.1 基于IAHP法的主观权重
区间层次分析法与传统的层次分析法相比,引入了区间数的概念[6],专家在实际打分过程中,往往会面临信息不完备或考虑因素复杂等问题,因此对于某个指标更愿意给出一个区间数而不是单点数值。
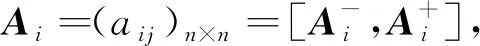
。
(1)
2) 计算系数p和q
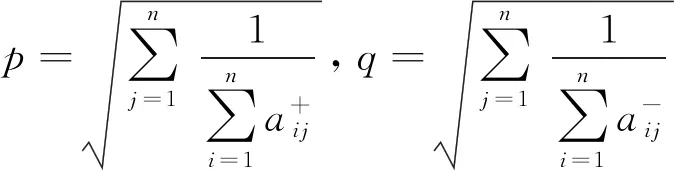
(2)
3) 计算权重
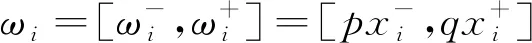
(3)
4) 取ωi区间端点的平均值作为各指标权重
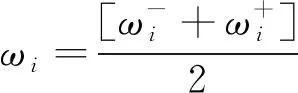
(4)
则各指标权重向量为ωsub=[ω1,…,ωi,…,ωn]T。
1.2.2 基于改进CRITIC法的客观权重
传统CRITIC法是通过衡量各指标间的差异性、冲突程度的标准差和相关系数来确定指标权重。然而由于不同指标间的数量级和量纲的差异性的影响,标准差在反映不同指标间差异性方面并不理想,且各指标间的相关系数可能存在负值,导致相关系数越小,指标冲突性越大[7]。
针对上述两个问题,本文提出改进CRITIC法,通过基尼系数[8]来衡量不同方案间指标的差异性,并考虑指标间正负相关系数情况,具体过程如下所述。
1) 评估指标预处理
评估矩阵Y由k个指标,m个评估对象构成。
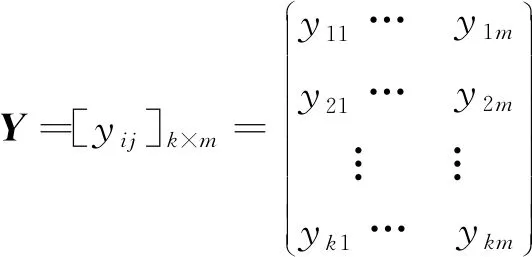
(5)
式(5)中,yij表示第j个评估对象对第i个指标的真实值。由式(6)对Y中的元素进行预处理,得到矩阵Z=[zij]m×k。

(6)
式(6)中,zjmin和zjmax分别表示第j个指标实际值的最小值与最大值。
2) 确定相关系数矩阵
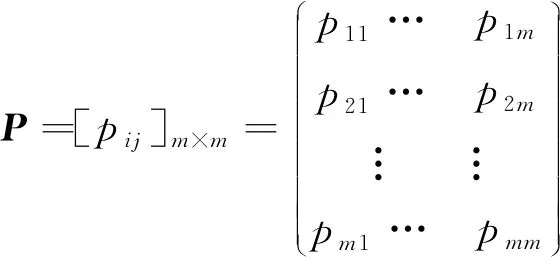
(7)
式(7)中,pij表示第i个指标和第j个指标之间的相关系数,由式(8)计算得到。
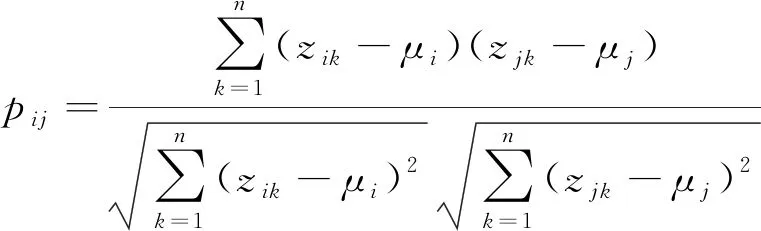
(8)
式(8)中,zik和zjk分别表示第i个指标和第j个指标下的第k个方案的指标标准值,μi和μj分别表示指标i、j的均值。
3) 计算基尼系数γi
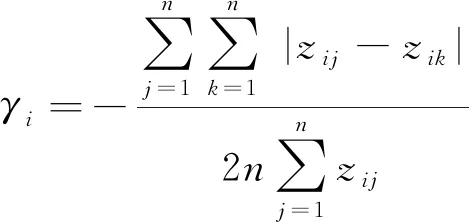
(9)
式(9)中,zij和zik和表示相同指标在不同决策方案下的标准值。
4) 计算指标间的冲突系数
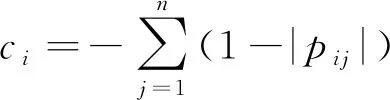
(10)
5) 确定指标客观权重
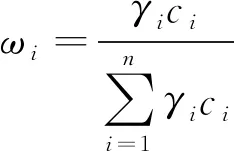
(11)
则各指标权重向量为ωobj=[ω1,ω2,…,ωn]T。
1.2.3 计算组合权重
基于IAHP法计算主观权重是根据专家的先验知识,改进CRITIC法计算客观权重是依据指标数据所包含的客观原始信息。组合赋权法综合考虑单一主观赋权和客观赋权的缺点,可使评估结果更加科学合理。目前,组合赋权法主要有加法和乘法两类。乘法组合赋权法在组合时存在“权重倍增”现象,即大的权值更大,小的权值更小;加法组合赋权法注重主客观权重的偏好,按照一定规则设计主客观权重偏好系数,更能体现组合赋权中主客观权重的贡献情况。本文采用加法组合赋权法,借助博弈论集化模型计算组合权重[9],具体方法如下所述。
假设存在l种不同的指标赋权方法,基础权重向量集ωk=[ω1,ω2,…,ωn]T,k=1, 2,…,l。则l种赋权法的线性组合权重为:
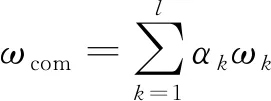
(12)
式(12)中,系数αk通过式(13)计算得到。

(13)
对系数αk作归一化处理:
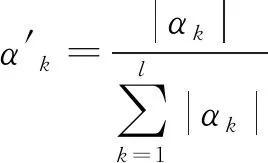
(14)
则指标组合权重为:
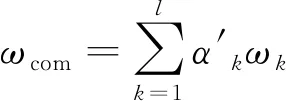
(15)
2 基于Vague集的预警卫星系统效能评估
2.1 Vague集基本理论
设存在一个论域U,x为其中任意一个元素,U中的一个Vague集A可由两个函数tA(x)和fA(x)表示,其中真隶属函数tA(x)是支持x的证据所推导的隶属度下界,假隶属函数fA(x)是反对x的证据所推导的隶属度下界,不确定函数πA(x)=1-tA(x)-fA(x)为x对于Vague集A的犹豫度,πA(x)越大,x对于A的不确定部分越多,称区间[tA(x),1-fA(x)]为A在元素的Vague值。tA(x)和fA(x)将闭区间[0,1]上的实数与论域U中的所有元素联系起来,即tA:U→[0,1],fA:U→[0,1],且0≤tA(x)+fA(x)≤1[10]。
当U离散时,Vague集A可表示为:
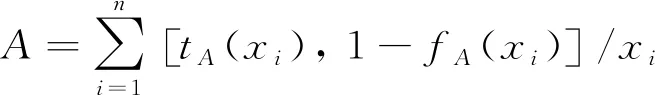
(16)
对于Vague值x=[tA(x),1-fA(x)],定义:
αx=(tx+txπx)-(fx+fxπx)=(tx-fx)(1+πx),
(17)
βx=(tx+txπx)+(fx+fxπx)=(tx+fx)(1+πx)。
(18)
则U中的两个Vague集A、B之间的相似度量定义为:
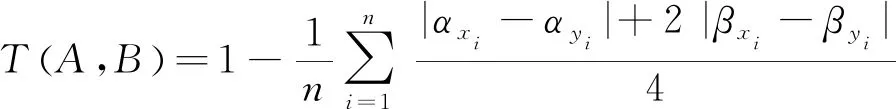
(19)
A、B之间的加权相似度量为:
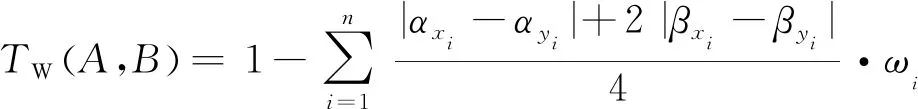
(20)
2.2 评估指标Vague集表示
评估指标通常可分为经济型(指标值越大越好)和成本型(指标值越小越好)两类,其Vague值表示方法如下:
设有指标集C=(C1,C2,…,Cn),方案集A=(A1,A2,…,Am),其中xij为Ai的第j个指标值。则区间数xij=[xij,yij]的Vague集值表示为
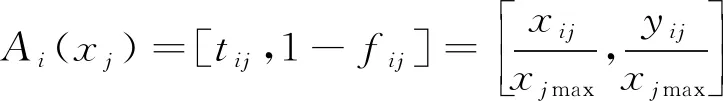
(21)
式(21)中,tij表示Cj满足Ai程度的下界,fij表示Cj不满足Ai程度的下界,且1≤i≤m,1≤j≤m,xjmax=max{x1j,x2j,…,xmj}。
单值数据xij可以看做特殊的区间数,即xij=[xij,xij],Vague集值为
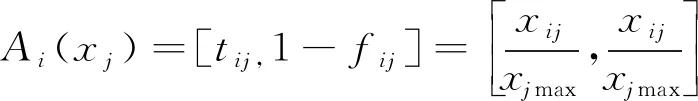
(22)
2.3 Vague集评估模型建立
依据经典模糊综合评价模型的分析过程[11],基于Vague集的预警卫星系统效能评估模型建立过程如下:
1) 构建预警卫星系统评估指标体系,如图1所示。
2) 计算指标组合权重。依照前文方法分别计算基于IAHP的主观权重和基于改进CRITIC的客观权重,并由博弈论极化模型得到组合权重。
3) 建立指标Vague集。区分经济型指标和效益性指标,由式(21)、式(22)将指标样本集表示为Vague集。
4) 构造理想Vague集。比较不同方案指标Vague值,得到理想Vague集B。
5) 计算加权相似度量,确定最优系统。根据式(17)-式(20)分别计算方案Ai与B之间的相似度和加权相似度。由Vague集综合决策规则可知,待评估系统Vague集与理想Vague集B加权相似度越大,该系统效能越好。
3 实例分析
3.1 计算指标权重
1) 计算指标主观权重
首先邀请50位相关领域专家对图1中给出的探测能力、识别能力、跟踪定位能力、预报能力指标权重进行打分,采用传统的层次分析法的1~9打分策略确定指标比较的区间数值,分层建立判断矩阵,检查一致性并求指标权重[12]。本文以预警卫星探测能力对其所属指标全球覆盖范围、重点区域覆盖范围、最大探测距离、探测概率4个二级指标的判断矩阵为例,判断矩阵C1如下:
将C1拆分为两个矩阵:
由式(1)分别求两个矩阵的最大特征根对应的归一化特征向量:
x-=[0.089 6,0.191 0,0.222 5,0.496 9]T,x+=[0.088,0.161 6,0.239 6,0.510 9]T。
再根据式(2)求得p=0.882 7和q=1.074 1,则指标主观权重向量为:
2) 计算指标客观权重
同样以预警卫星探测能力对其所属指标的评价矩阵为例进行说明。假设某地于某时从某基地发射场发射某型弹道导弹攻击L城,采用4组不同的预警卫星系统(即方案A1、方案A2、方案A3、方案A4)对其进行探测,4组方案全球覆盖范围、重点区域覆盖范围、最大探测距离以及探测概率所构成的评价矩阵Y为:

根据式(5)—式(11)即可得到上述4个指标的客观权重值:
ωobj=[0.201 4,0.359,0.179 7,0.259 9]T。
3) 计算组合权重
结合上述主客观权重向量,根据式(12)—式(15),指标组合权重
ωcom=[0.174,0.314,0.191,0.316]。
按照上述步骤即可求得预警卫星系统其他指标权重值,结果如表1所示。
3.2 建立样本集
现对A1、A2、A3、A4这4类预警卫星系统探测效能进行评估,构成方案集A=(A1,A2,A3,A4),由图1构建的评估指标体系形成指标集,结合各系统作战效能得到各指标样本值,如表2所示。
3.3 建立指标Vague集和理想Vague集
根据式(21)—式(22)将表2中的原始样本数据进行转换,得到所有指标的Vague值评价数据,结果如表3。
区分成本型指标和效益型指标,得到理想Vague集B,结果如表4所示。
3.4 确定最优系统
由式(20)计算方案A1、A2、A3、A4的Vague集与理想Vague集B之间的加权相似度:TW(A1,B)=0.851;TW(A2,B)=0.905;TW(A3,B)=0.847;TW(A4,B)=0.867。
由Vague集综合决策规则可知,待测系统Vague集与理想Vague集B之间的加权相似度越大,则该系统效能越好。因此,4个方案的效能排序结果为:A2>A1>A4>A3,即方案A2对应的预警卫星系统效能最优。
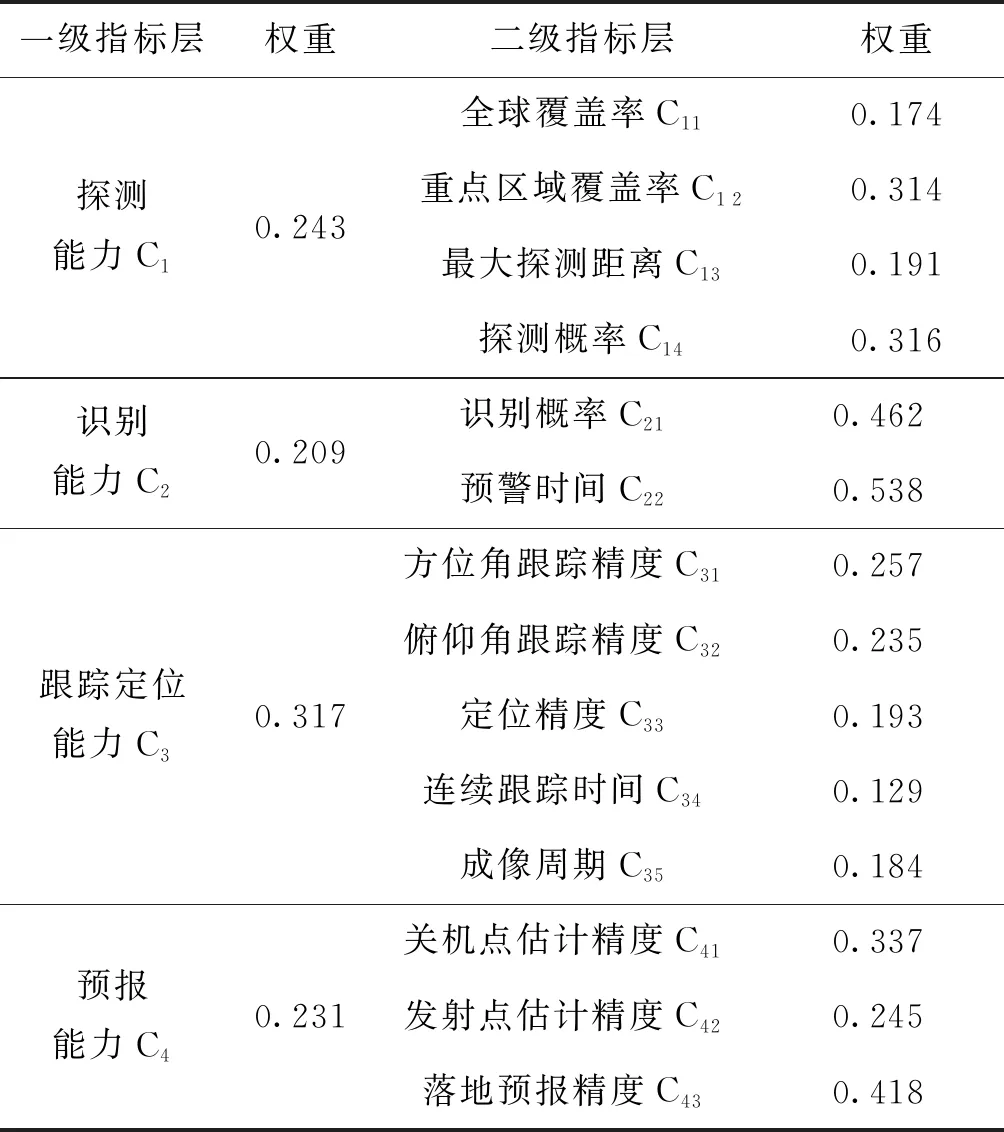
表1 预警卫星系统评估指标体系权重Tab.1 The weight of the early warning satellite system evaluation indicator system
4 结论
预警卫星系统效能评估实际上是一个多指标综合决策过程,且涉及到定性和定量的指标。本文提出基于主客观组合赋权与Vague集理论相结合的预警卫星系统效能评估方法。利用IAHP法得到系统评估指标的主观权重,改进CRITIC法得到客观权重,由博弈论集化模型将主客观权重相结合得到组合权重;综合考察定量和定性指标的优劣,构造理想Vague集,利用Vague集综合决策规则评估预警卫星系统效能优劣。仿真实验结果表明,该方法能够较客观地反应预警卫星系统效能,为后续预警防御系统整体探测效能的评估提供了参考依据。

表2 预警卫星系统指标样本集Tab.2 Sample set of early warning satellite system indicators
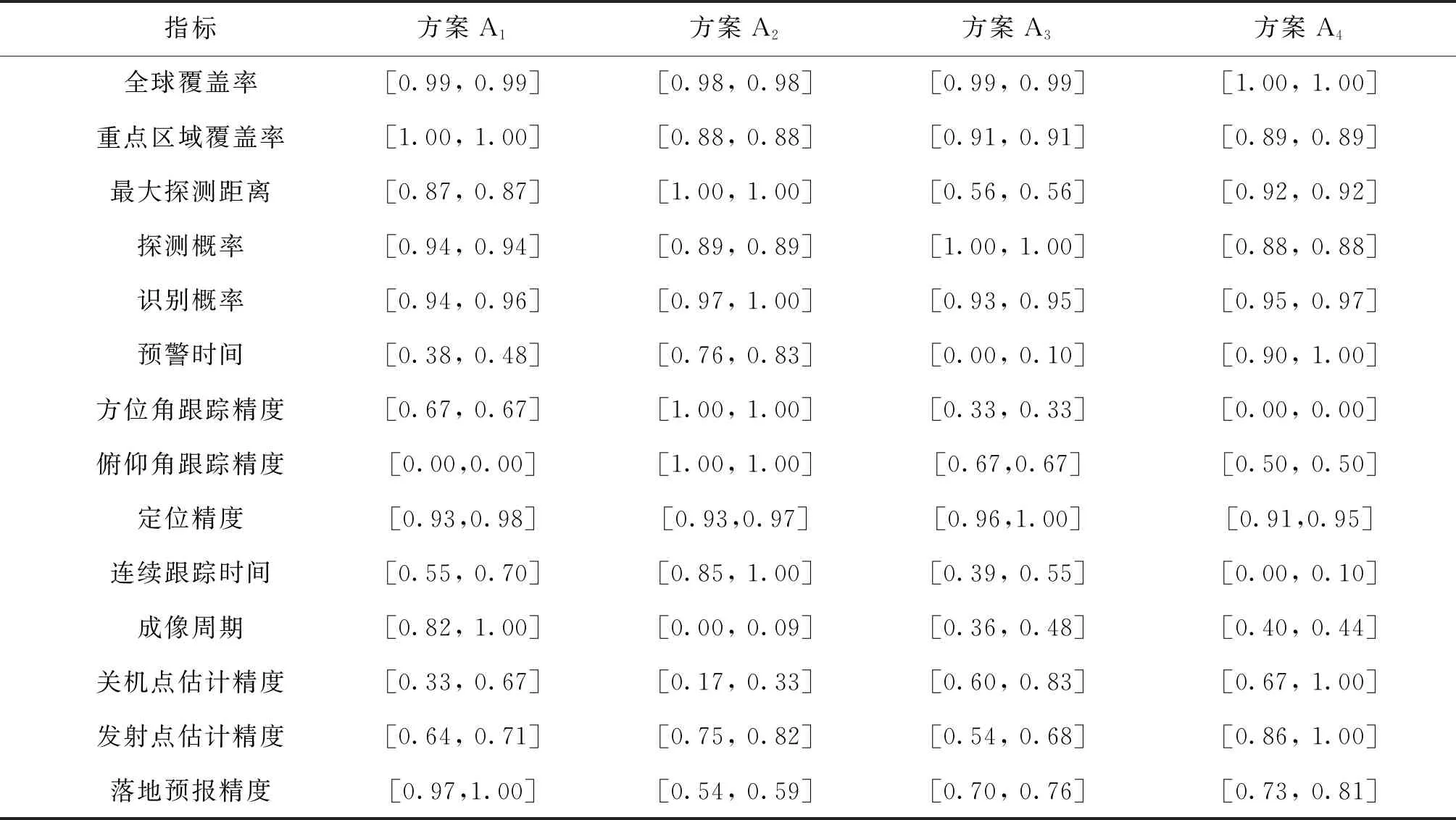
表3 预警卫星系统指标Vague集表示Tab.3 Vague set representation of early warning satellite system indicators

表4 预警卫星系统指标理想Vague集表示Tab.4 Representation of ideal Vague set for early warning satellite system indicators

