地铁和多中心结构如何影响中国大城市的人口增长？

魏守华 黄 和 吴海峰

(南京大学，江苏 南京 210093)

一、引言与文献综述

近30年来，中国城镇化率从1990年的26.41%迅速上升到2020年底的63.89%，年均新增城镇人口1500万人左右，堪称人类发展史的奇迹(魏守华 等，2021)。但是，城市间的人口增长率并不“平行”，而是呈现特大城市规模迅速膨胀而中小城市相对萎缩的两极化现象(魏后凯，2014)。以第五～第七次全国人口普查数据为例，2000年末中国35个大城市的人口规模为14666万人，2020年末为30088万人，20年间人口增长率为105.15%，平均每个城市人口规模净增加441万人，城市规模迅速膨胀。按照城市经济学的经典理论，城市人口规模取决于正向集聚效应与负向拥挤效应的权衡(奥沙利文，2013)。那么这两种效应在中国(特)大城市中是如何体现的？

现有文献主要从集聚效应角度解释中国大城市人口的快速增长，特别是认为政策偏向使高等级城市(大城市)人口持续增长。魏后凯(2014)认为，中国城镇化进程中存在明显的行政中心偏向，导致城市规模与行政等级显著相关。年猛等(2016)回顾了改革开放以来城市发展政策，认为政策显著偏向高等级行政中心，促成一批特大城市，甚至是超大城市出现。邓涛涛等(2019)发现，在交通状况日益改善的背景下，中国大城市的集聚效应更加明显，如高铁建设对大城市人口规模增加的正向作用要高于中小城市，导致人口规模分布的两极化。魏守华等(2020)认为，国家的经济导向政策和土地供给政策是导致中国高等级城市(大城市)和低等级城市(中小城市)人口增长差异的重要原因。可以看出，已有文献少有从拥挤效应或通勤成本角度解释这一现象，本文基于集聚效应，侧重于交通技术进步，即从地铁建设及多中心空间结构角度解释中国特大城市人口快速增长现象。

运量大、运行效率高、绿色环保的地铁是中国城市建设中的新兴公共交通工具，极大地提高了居民的出行便捷度。1971年中国第一条城市地铁在北京开通，截至2000年，只有北京、天津、上海和广州四个城市开通地铁。但2000—2010年，大连、长春、武汉、重庆、深圳、南京、成都、沈阳陆续开通城市地铁。截至2020年，全国已经有41个城市开通地铁，尤其是副省级城市和省会城市基本开通地铁。此外，一些经济发达的大城市，如苏州、无锡、常州、温州等也已开通地铁。根据2019年的数据，全国地铁交通运营线路长度为5531.51公里，客运量达到233.1亿人次，地铁每公里客运量约为传统交通工具的14.8倍。地铁建设与交通网络的形成会大幅度降低通勤成本，减缓拥挤效应，有助于城市人口的增长。

关于地铁如何促进大城市人口规模增长，现有文献主要分两方面进行分析：一是地铁等交通基础设施建设会降低居民的通勤成本而有助于城市规模增长。Gonzalez-Navarro et al.(2018)基于对全球632个大城市的地铁建设(以站点数量、线路数量和基于站点经纬度计算的线路长度来衡量)，研究发现地铁建设对城市人口增长的作用比较微弱。肖挺(2021)以地铁运营长度衡量地铁建设水平且加入地铁开通虚拟变量，通过Heckman两步法和门限回归方法检验地铁开通对全要素生产率尤其是环境生产率的积极影响。这意味着地铁建设可以促进城市生产率和改善环境效应，间接有助于城市人口规模的增长。二是地铁建设影响城市空间形态——空间结构，并间接地影响城市人口增长。Baum-Snow et al.(2017)探究了公路和铁路对中国城市形态，尤其是城市人口与产业扩散的影响，研究发现放射状和环状的公路都会促使人口和经济活动由市中心向外围转移。Gonzalez-Navarro et al.(2018)对全球632个大城市的研究发现，地铁建设会引起城市人口和产业由中心地区向外围的分散化。华杰媛等(2015)基于2010年的城市截面数据，运用与人口密度、首位度概念等相关的四个指标衡量107个大都市区的多中心结构，实证结果显示，多中心的空间结构有益于提高大都市区的经济绩效。王峤等(2021)间接地考察了空间结构对城市经济增长的作用，发现城市多中心化会抑制创新，但城市人口规模扩张能够缓解这一不利影响。Li et al.(2018)认为，城市空间结构的经济效应在不同等级城市之间存在差别，人口密度更高的城市因能够从多中心形态中获益而生产率较高，这一促进效应可能与主中心、次中心之间的可达性有关。总的来看，现有文献较少将地铁与中国城市的人口规模、内部空间结构直接联系起来，从经济学角度分析城市地铁建设水平在其中的作用。此外，在测度城市多中心度时，使用的数据不够完美，如间隔期偏长(10年)的全国人口普查数据，或是较为间接的夜间灯光数据。

本文考虑包含生产者与消费者的两部门基本模型，并聚焦于住房和通勤成本，设定居民(消费者)的效用函数，探讨地铁对城市规模增长的促进作用以及多中心结构的中介效应。此外，本文使用城市连续多年、分市辖区的常住人口数据，设计新的多中心结构指标，在测度城市多中心结构时有一定创新性。

二、理论分析及假说提出

参考Henderson(1987)、魏守华等(2020)分析城市体系中单个城市有效规模的思路，构建理论模型，阐释地铁对城市规模增长的促进作用以及多中心结构的中介效应。

(一)基本设定

城市居民的效用函数设定如下：

U=λ(t)HZ

(1)

其中， H和Z分别为住房和住房以外的其他商品的消费量，λ(t)为生活舒适度。住房与其他商品是城市生产的两类最终产品。城市生活舒适度作为居民效用的一部分，可以被纳入直接效用函数(刘修岩 等，2019)，具体形式如下：

λ(t)=θe

(2)

其中：θ表示除交通条件之外，公共服务、生态环境等其他影响生活舒适度的因素，由于本文模型主要分析地铁的作用，因此将其设定为外生变量；t表示城市内部单位距离的通勤时间，体现交通基础设施对居民效用的影响，t越大表示居民投入在通勤上的时间比重越大。简言之，交通基础设施的完善，尤其是地铁的建设，有利于降低通勤成本，从而优化居民的通勤和生活体验，提高居民的满意程度。

(二)地铁建设与人口规模

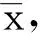
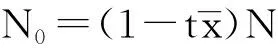
(3)

假定城市生产住房和其他商品的规模报酬不变，其中其他商品的生产需要投入劳动与资本两种要素，其生产函数如下：

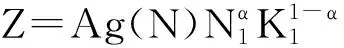
(4)

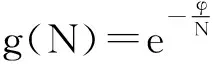
住房的生产函数为：

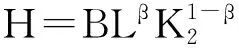
(5)

住房的生产中所投入的生产要素为土地与资本，其投入量分别以L与K表示，B表示生产效率参数。其中土地要素L的利用可视作中间产品的生产(Henderson，1974)，表示如下：

L=(DN)N

(6)

其中：D表示生产效率参数；N表示投入到土地开发中的劳动力，满足N=N-N；δ表示地形复杂度，地形越复杂则土地产出越低(魏守华 等，2020)。

假设资本的价格利息率r是外生给定的，其他商品生产的利润最大化条件有：

MPN×p=w

(7)

MP×p=r

(8)

其中，MPN和MP分别表示劳动力和资本的边际产品，p是贸易品的价格。结合以上两式可以将其表示为：

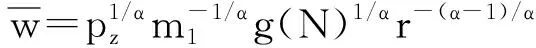
(9)

其中，m=Aα(1-α)。

同理，住房的价格p可以表示为：

p=mNwr

(10)

其中，m=BD。

对于城市整体而言，总收入为有效劳动投入获得的工资总和：

(11)

由于有效劳动供给中已经考虑了通勤成本的影响，因此城市居民的预算约束包含住房和其他商品的消费：

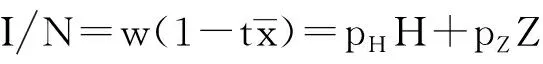
(12)

城市居民的目标是最大化其效用，即max[λ(t,N)HZ]，并且受到式(12)条件的约束。可求得，居民效用最大化时，住房和其他商品的需求分别为：

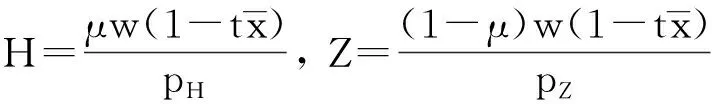
(13)

将式(13)和式(9)、(10)、(11)代入效用函数中，得到居民的间接效用函数：

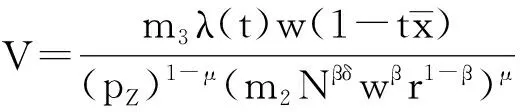
(14)

其中，m=μ(1-μ)。

将式(2)代入式(14)，进一步整理得到：

V=φe(e)N=φeN

(15)

令∂V/∂N=0，得到城市有效人口规模：

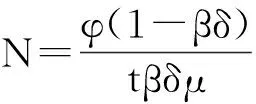
(16)

由式(16)可知，城市通勤成本t降低会使城市总人口增加。此外，土地的产出弹性β、地形的复杂度δ和住房的消费倾向μ都会负向影响城市规模。地铁建设缓解了城市的交通压力，降低城市整体的通勤成本，有助于城市人口规模的增长。由此，得到：

假说

1

：

城市地铁建设有利于降低通勤成本，提升城市人口规模。

(三)地铁建设与城市多中心结构

在城市经济学中，经典的假设为单中心城市模型，即就业集中于城市中心(中央商务区)，而居住区分布在外围(丁成日，2006)。初始的单中心结构与城市最终可能形成的多中心结构并不矛盾，McMillen(1996)认为多中心结构下初始的中央商务区仍可能占据主导地位。在中国，随着城市规模的扩大和交通技术的进步，许多城市正从单中心结构向多中心结构演变(魏守华 等，2016)。因此在以上模型的基础上，本文基于效用函数的设定，进一步讨论地铁建设对城市多中心结构的影响。

地铁建设会影响城市单位距离的通勤时间t，但对居住在不同城市区位的居民影响不同。将城市中心视为一个点，居民居住在市中心外围，到市中心的距离为x。初始情况下，所有居民都要前往市中心就业，通勤距离也为x，居民的收入为w-tx。与前文一样，居民的有效收入分配于住房和其他商品的消费。那么居民的预算约束为：

w(1-tx)=Z+pH

(17)

其中，H和Z仍然分别表示住房消费和其他商品消费。与前文有所不同的是，将其他商品的价格设定为1，以简化分析，而住房价格p受到位置(即到市中心的距离)等因素的影响。可以求得居民效用最大化时，住房和其他商品需求分别为：

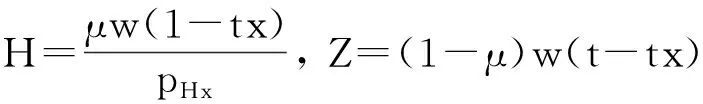
(18)

将商品需求代入效用函数中，得到间接效用函数：

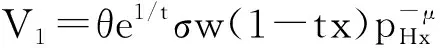
(19)

其中，σ=(1-μ)μ。居民的偏好、消费倾向等特征都相同，且在城市中自由移动，这意味着不同区位的居民效用具有无差异性，设到市中心距离不同的居民都将达到同一效用水平V，由此住房价格可表示为：

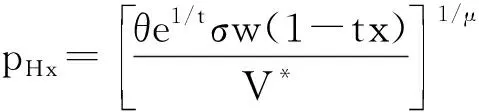
(20)

易求得，∂p/∂x<0，这说明随着到市中心距离的增加，住房价格将逐渐降低。住房需求中，有∂H/∂p<0，进一步得到∂H/∂x=∂H/∂p×∂p/∂x<0，这说明住房消费量将随着到市中心距离的增加而提高。这两组关系表明，不同地点居民的效用水平相同，住在相对外围区域的居民面临更高的通勤成本，而获得较低的住房价格作为“补偿”。由于消费者替代的存在，价格较低时，居民可能会选择更大面积的住房：

Δp×H(x)+Δx×t=0

(21)

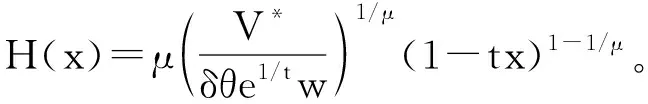
可得住房曲线的斜率为：

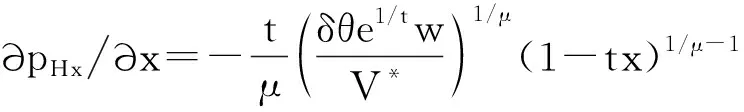
(22)

由式(22)可知，在其他条件不变的情况下，单位距离通勤成本t降低时，住房价格函数的斜率绝对值也减小，住房价格曲线将向逆时针方向旋转，变得较为平坦，如图1所示。

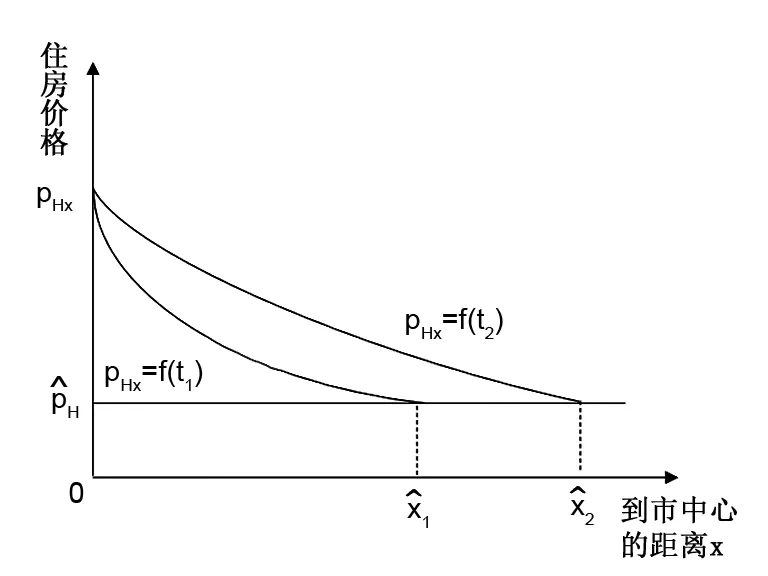
图1 通勤成本变化与住房价格

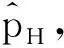
假说

2

：

地铁建设有助于扩大城市建成区面积，增加城市规模。

前文假设城市居民均在市中心就业，接下来假设在距离市中心处d有一个新的就业中心，分析城市次中心形成的影响因素。

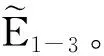
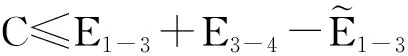
(23)

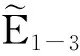
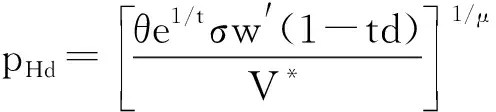
(24)

其中，d表示从居住地点到次中心d的距离。

再转换为从居住地点到市中心距离x的函数为：

(25)

则

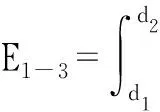
(26)

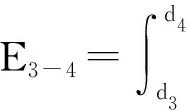
(27)

另外，基于式(20)计算得出机会成本为：

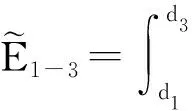
(28)

将式(26)～(28)代入式(23)，得到式(29)，表示如下：

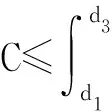
(29)

通过对式(29)右侧求导可以得出，城市次中心建设的可能性随t的减小而增大。因此随着地铁的修建，城市通勤成本降低，住房价格曲线将如图2所示，会出现次一级的集聚中心，城市呈现多中心形态。由此，得到：

图2 次中心建设与住房价格

假说

3

：

地铁建设有助于城市形成多中心结构。

由前文和图2可知随着城市次中心的建设，次中心的房价将会高于单中心时期同一路段的房价，因而居民将只能买得起更少数量的房屋。在同一区位房屋数量一定的前提下，该区位将会容纳更多数量的居民。因此，可以得出城市房价越高的区位，人口数量也会越多。而随着城市次中心的形成，d-d区段的房价均高于单中心时的房价，且次中心的建设使得城区面积扩张到了d-d路段，这两种影响均会使得城市人口增加。这进一步验证了式(16)关于城市人口影响因素的结论。综合以上讨论，得到：

假说

4

：

地铁建设下的城市多中心结构会优化城市形态，推动城市人口规模增长。

三、研究设计与变量说明

(一)模型设定

借鉴年猛(2021)的城市人口增长模型，构建地铁建设影响城市人口增长的模型：

ln(P/P)=β+βln Subway+βln Agglom+βX+ε

(30)

其中：P/P为i城市t到t+1时期市辖区的常住人口增长率；Subway表示地铁建设后的路网密度，代表城市的拥挤效应对城市规模增长的影响；Agglom表示集聚经济效应，反映其对推动城市规模增长的作用；X表示一系列影响城市规模增长的控制变量，如初始规模、政府投资、产业结构、自然条件等；ε为误差项。

(二)变量界定与测度

1.被解释变量

被解释变量以人口增长率的自然对数ln(P/P)来表示。

2.核心解释变量

地铁指标，以地铁里程密度(地铁里程/建成区面积)来表示。需要说明的是，地铁建设对城市规模的影响有滞后效应，因而本文将式(30)中的关键解释变量滞后一期。

3.控制变量

为了使模型更符合实际情况，减少遗漏变量带来的误差，本文选取以下控制变量：

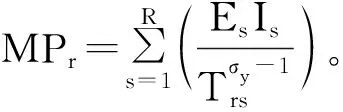
(2)初始城市规模(City Size，CS)。初始城市规模(取对数，记作ln CS)会产生集聚效应和拥挤效应。Eeckhout(2004)论证了当居民在城市间无成本地自由迁移且城市间效用函数恒等的情况下，城市规模将“等比例增长”，ln CS的系数将不显著。在中国，一方面，大城市居民的效用函数显著高于中小城市和农村，人口会向大城市集中；另一方面，特大城市规模过大导致拥挤效应日益增强，国家逐渐加强对特大城市规模的管控。在回归分析中，将ln CS滞后到t-1期。

(3)公共财政支出(Fiscal Spending，FS)，反映政府对城市发展的干预作用，以城市公共财政支出占地区生产总值的比重表示。

(4)产业结构(Industrial Structure，IS)，以第二产业与第三产业产值比值表示，数值越大表示城市的第二产业相对越发达。第二产业与第三产业的就业吸纳能力、区位与交通条件要求不同，产业结构可能影响城市规模与地铁建设。

(5)道路密度(Road Density，RD)，以城市公路道路长度与建成区面积之比表示。地铁与城市道路存在着一定的互补与替代的关系。这个指标的系数为正，表明公路密度与地铁密度具有互补性；如果系数为负，则表明地铁密度与公路密度具有替代性。

(6)城市的自然环境指标。优越的自然环境会增强城市居民的舒适度(王垚 等，2015)。选择年平均气温(Temp)与年降水量(Prcp)作为自然环境的代理变量，均进行自然对数处理。

(三)数据来源与描述性统计

本文的“城市”是指城市市辖区范围内的常住人口。但现实中，有的城市在考察期内存在行政区划的变动，如撤县设区。如果统计时不考虑区划变动，则会错误估计真实的城镇人口。因此，本文以2019年末各城市市辖区区划为基准，对历年有区划变更的城镇进行调整，使每个城市的行政区范围尽可能保持一致。

本文的被解释变量与中介变量均涉及城市常住人口，通过以下方法得到：首先，收集城市各市辖区每年的常住人口数据；其次，对其进行加总得到城市每年的人口规模。具体来源是《中国2010年人口普查分县资料》以及各城市或对应省份的统计年鉴。

地铁里程数据来自《中国城市建设统计年鉴》中的分城市轨道交通数据，并且将“建成”与“在建”两部分进行加总。这样的做法是考虑到地铁开通存在“试运营”的阶段，而统计中这一阶段的数据可能被计入“在建”一栏。另外，居民也可能根据城市地铁建设规划进行区位选择，因此建设中的地铁也会对城市规模产生潜在的影响。考虑单位面积的地铁建设情况，土地面积数据来自《中华人民共和国行政区划简册》。控制变量数据来自《中国城市统计年鉴》《中国城市建设统计年鉴》和各地区的统计年鉴。对于有些数据零散或缺失的情形，根据前后年份的数据进行平滑处理和填补。

截至2019年，内地有近40个城市开通了地铁，考虑到数据的完备性与可得性，最终选择其中的20个城市为研究对象，考察期为2011—2019年，解释变量因滞后一期而为2010—2018年。此外，之所以选择2010年为研究起点，是因为：第一，2010年进行了第六次全国人口普查，可以获得高质量的区县层面的常住人口数据。这部分数据是本文测度城市多中心度的基础。第二，内地城市的地铁大部分是在2010年之后开通的。第三，从2009年开始，《中国城市建设统计年鉴》才明确“建成”与“在建”轨道交通统计的区分。简言之，以2010年为时间起点，本文的数据较为完善。

表1呈现变量的含义与描述性统计结果。

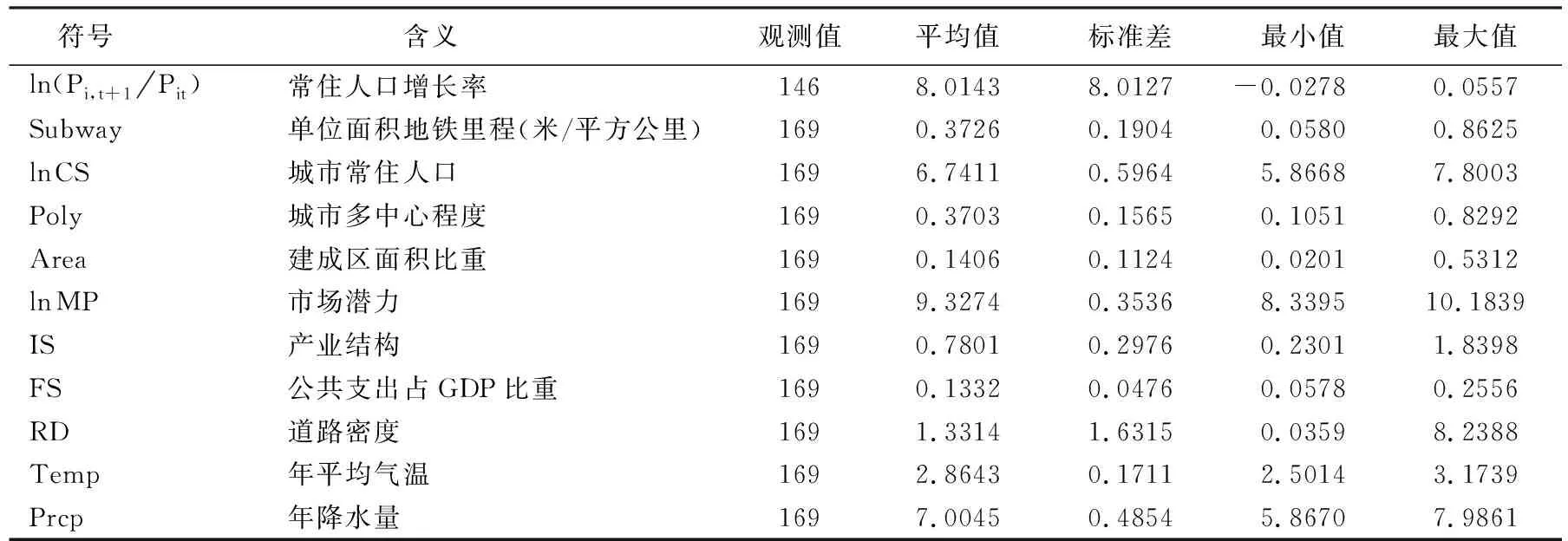
表1 变量含义与描述性统计

四、回归结果及其解释

(一)基准回归结果

为了检验地铁建设对城市常住人口增长率的影响，基于式(29)验证假说1，结果见表2。列(1)、(2)为混合OLS模型，列(3)、(4)为固定效应模型；列(1)、(3)仅有核心解释变量，列(2)、(4)则加入控制变量。可以看到，无论是否加入控制变量、采用何种模型，核心解释变量地铁里程密度(ln Subway)的系数都显著为正，且均在1%水平上显著。这表明，地铁建设有助于提高人员流通的效率，降低通勤成本，拓展城市建成区的空间，增加城市的人口规模。假说1得到支持。

表2固定效应模型中的其他关键解释变量均显著。初始城市规模(ln CS)的系数显著为负，表明初始城市人口规模较大的城市，人口增长率相对较低，城市规模有趋于稳定态的趋势。市场潜力(ln MP)的系数显著为正，表明城市集聚效应越大，城市人口增长率越高，说明中国特大城市人口增长也受益于集聚经济效应。除道路密度外，其它控制变量的系数均不显著，但不影响本文的核心论点。

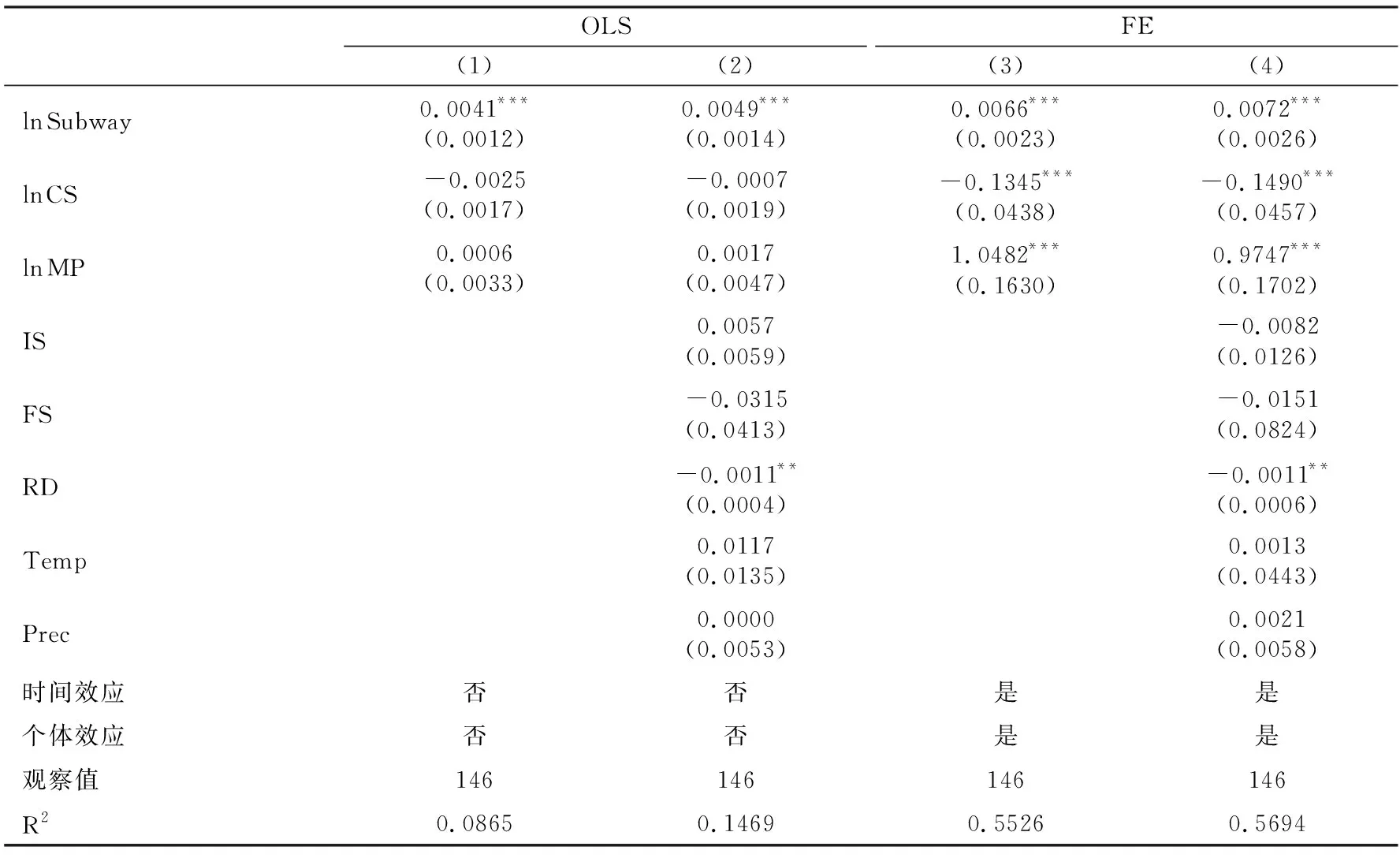
表2 基准回归结果

(二)稳健性检验

1.替换地铁指标

为保证基准回归结果是稳健可信的，本文进行稳健性检验。使用不同的地铁度量指标，从不同角度反映地铁建设对城市人口规模增长的影响，并缓解关键解释变量指标选择带来的偏误，具体如下：

(1)使用城市地铁站点数量/建成区面积的对数值(可称为“地铁站点密度”，ln Station)作为核心解释变量。地铁站点数量与里程都体现了地铁建设对城市的覆盖范围，而且地铁站与居民的出行选择直接对接。地铁站的建设能够同时反映地铁建设的广度和深度：一方面，在城市相对外围的区域设置地铁站，提升了该区域的通达性；另一方面，根据城市人口和产业的空间分布有序地规划站点，能够更高效地发挥地铁的作用，提高居民出行的便利程度。表3的列(1)、(2)使用地铁站点密度(ln Station)作为核心解释变量，其它变量均不变。可以看到，不论是否加入控制变量，地铁站点密度(ln Station)的系数均为正，且在1%的水平上高度显著；同时，地铁站点密度(ln Station)的系数相对于地铁里程密度(ln Subway)的系数更大，反映了地铁站点数增加带来的人口增长更明显。

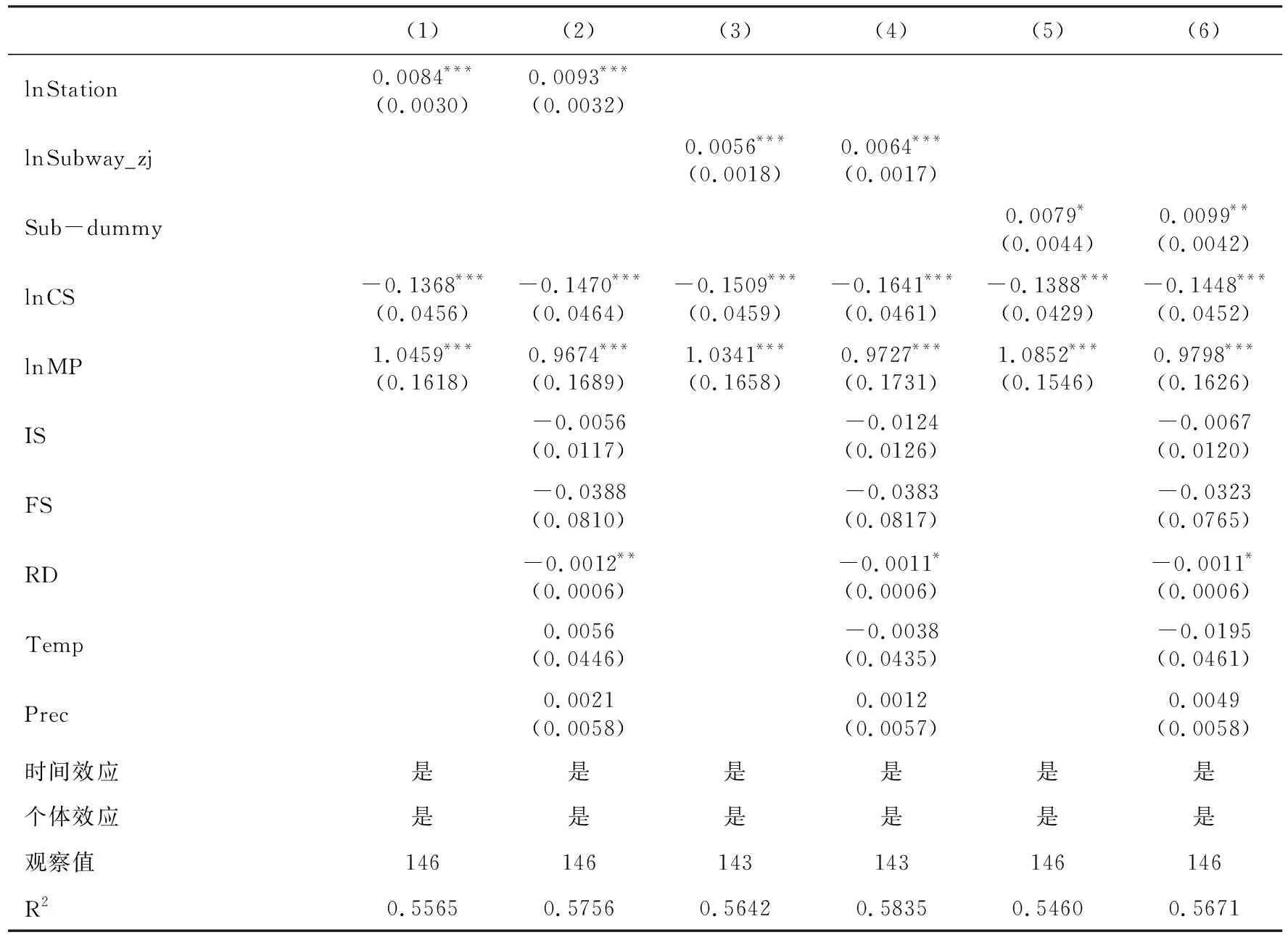
表3 稳健性检验：替换地铁度量指标

(2)使用城市在建地铁里程数/建成区面积的对数值(可称为“在建里程密度”，ln Subway_zj)作为核心解释变量。前文以“在建”和“建成”地铁里程数总和构建地铁建设指标，考虑到城市“在建”地铁里程数能够反映城市未来的空间发展重点，影响居民的区位选择和城市的规模增长，故用“在建”地铁里程数构造在建里程密度(ln Subway_zj)，其它变量均不变。回归结果如表3列(3)、(4)所示，可以看到，不论是否加入控制变量，在建里程密度(ln Subway_zj)的系数均显著为正，且系数相对于地铁里程密度(ln Subway)较小，反映了城市在建地铁里程密度提高有助于人口规模增长，同时也表明城市已建成的地铁对人口集聚增长的促进作用不可忽视。

(3)使用地铁开通年份虚拟变量(Sub-dummy)作为核心解释变量，开通年份之前为0，开通当年及以后为1。地铁开通后能够降低城市通勤成本、扩大城市半径，采用地铁开通年份虚拟变量(Sub-dummy)能够反映地铁建设带来的影响，其它变量均不变。回归结果如表3列(5)、(6)所示，可以看到，地铁开通年份虚拟变量的系数在加入控制变量前后均显著为正，说明城市地铁在建或建成后对于人口增长均具有促进作用。

2.剔除部分城市

近年来，中国开通地铁的城市越来越多，而新近开通地铁的城市，地铁对人口规模增长率的作用可能更明显。因此，本文剔除了2015年及以后开通地铁的城市(青岛、南宁、厦门)，剔除后样本城市共有17个，回归结果如表4列(1)、(2)所示。可以看到，结果仍然稳健，地铁里程密度的系数比表2基准回归相应的系数都有所减少，说明新近地铁开通带动人口规模增长的作用更明显。此外，城市开通地铁需要考虑拥挤效应和集聚效应的平衡，在跨越人口门槛后修建地铁带来的人口规模增长可能更显著。因此，本文剔除了2010年城镇人口小于300万的城市样本(福州、南宁、厦门)，表4列(3)、(4)汇报了人口门槛以上的17个城市样本的回归结果。可以看到，结果依然稳健，地铁里程密度的系数比表2基准回归相应的系数都有所增加，说明跨越人口门槛的城市开通地铁对人口规模增长的促进作用更大。

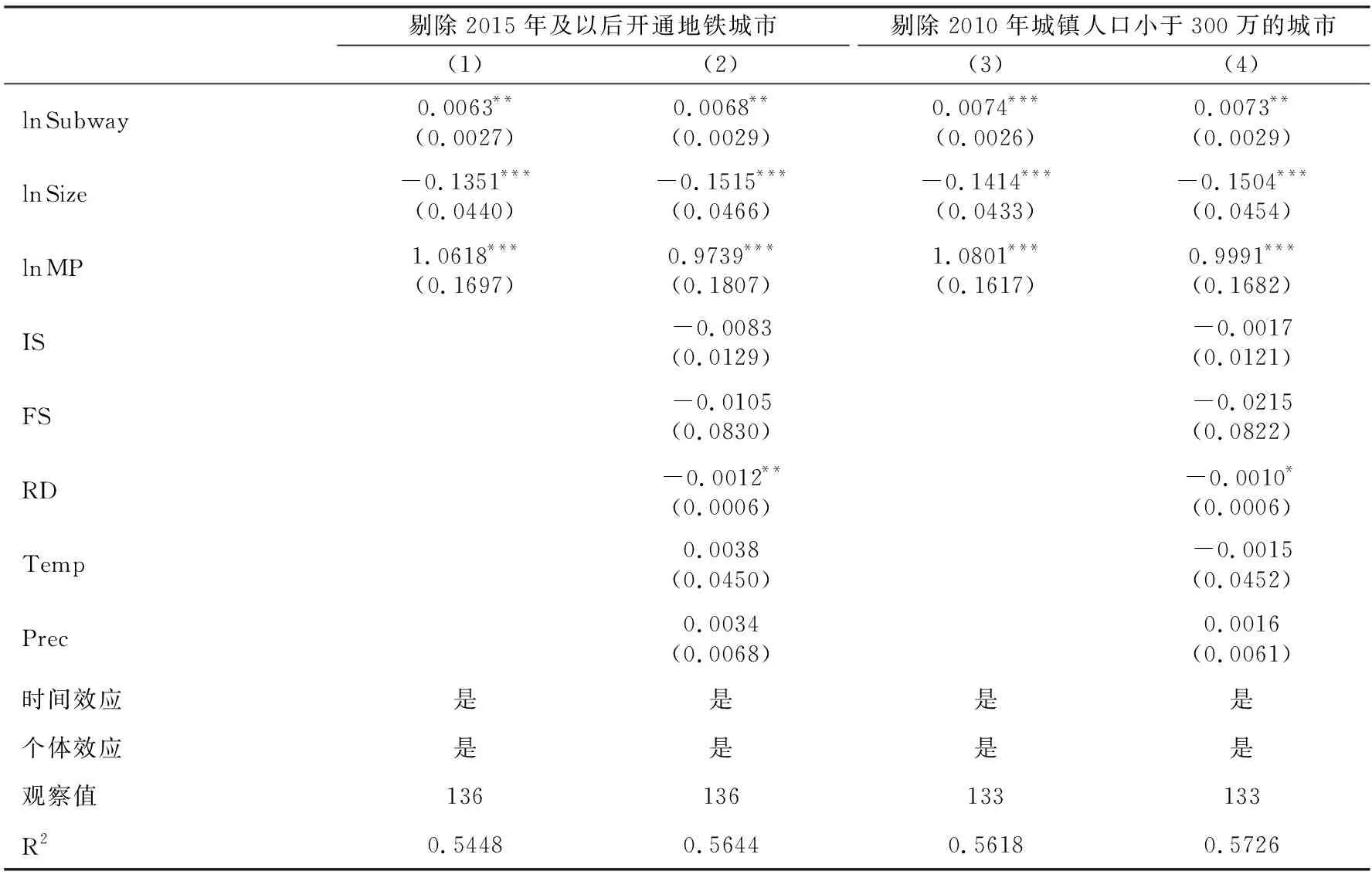
表4 稳健性检验：剔除部分城市

3.内生性与工具变量

在基准回归和稳健性检验中，尽管将核心解释变量与控制变量分别进行滞后处理，削弱了双向因果关系带来的内生性，但是仍可能存在遗漏变量造成的偏差，因此尝试使用工具变量法对此进行处理。本文分别采用滞后两期的地铁里程密度和处理后的地铁里程密度作为工具变量。其中，自变量的滞后项是常见的工具变量，其相关性与外生性容易满足，回归结果如表5列(1)、(2)所示。可以发现，地铁里程密度的系数仍然显著为正，初始城市人口规模和市场潜力的系数也符合预期。此外，考虑到地铁统计数据可能存在跳跃幅度过大的缺陷，本文将处理过的地铁里程密度作为工具变量。具体处理方式是：利用各城市样本期第一年和最后一年的地铁里程，计算样本期内地铁里程的几何平均增长率，再推算出中间各年的地铁里程数据。处理过的地铁里程指标由于首尾两期数据采用实际数据而与原地铁里程指标相关，且因采用几何平均增长的方式填充中间年份数据而不受当期外部冲击的影响，符合工具变量的假设，回归结果如表5列(3)、(4)所示。可以发现，结果仍然稳健。总的来看，地铁里程密度的系数均增大，表明潜在的内生性可能起到的作用被低估，工具变量的回归结果进一步支持了本文的主要结论。

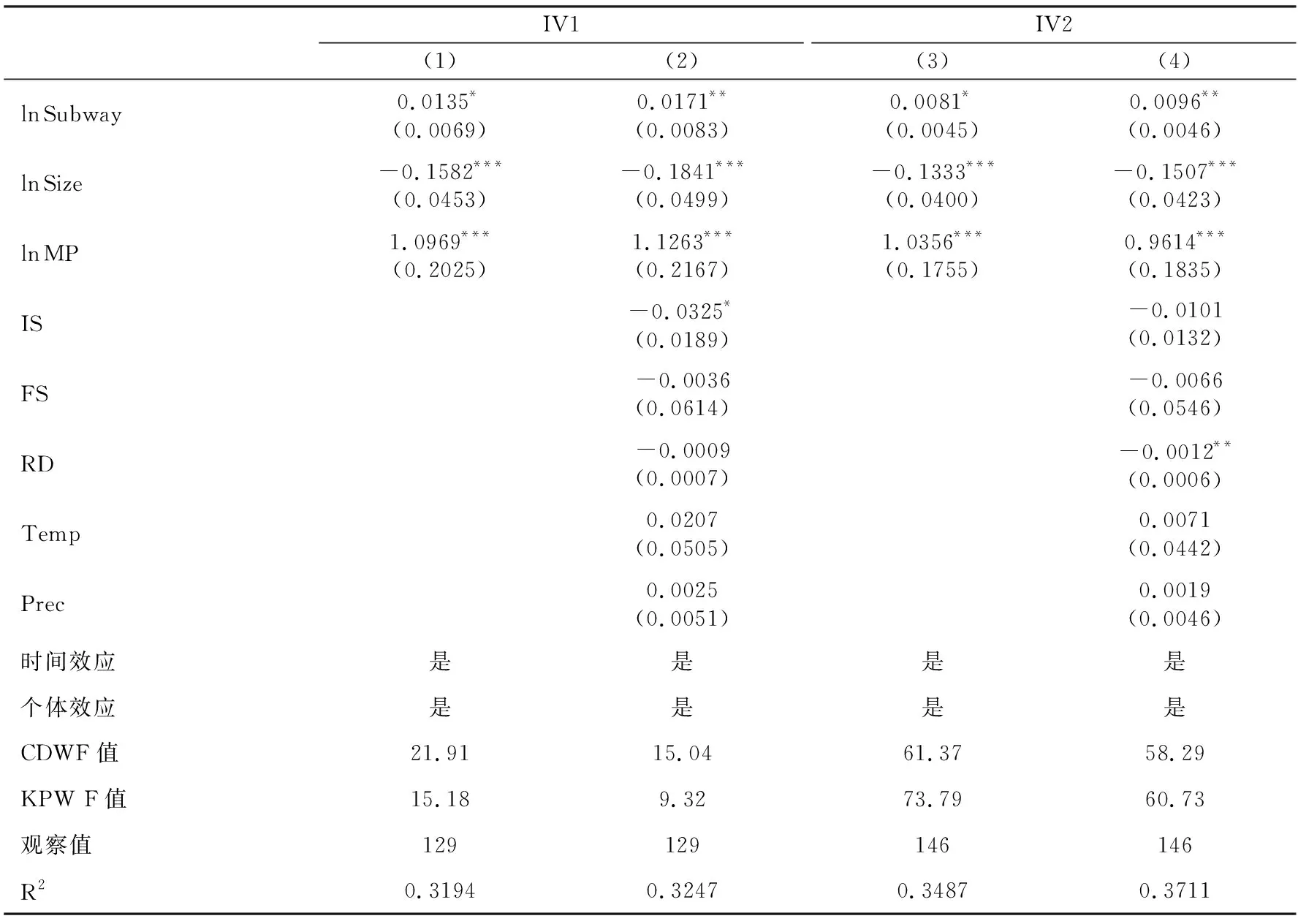
表5 工具变量回归

五、多中心空间结构与中介效应回归

(一)中介效应模型

上文的理论假说认为，地铁建设通过促进城市多中心发展和建成区面积扩张，进而影响城市人口规模。借鉴Baron et al.(1986)、邵帅等(2020)的做法，采用逐步法实证检验该理论假说，构建如下中介效应模型：

mediat=α+αln Subway+αX+φ

(31)

ln(P/P)=γ+γln Subway+γln Agglom+γmediat+γX+ζ

(32)

其中：ln(P/P)为人口增长率；ln Size为滞后一阶的城市初始人口规模；ln Subway为滞后一阶的地铁里程密度；X为市场潜力以及其它控制变量；mediat为可能的中介变量且作滞后一阶处理，包括城市建成区面积占比(以城市的建成区面积/全市面积(Area)表示)、城市的多中心程度(以次城区常住人口/市辖区常住人口的对数值(ln Poly)表示)。

(二)城市多中心结构的界定与测度

早期的城市空间组织多是单中心结构，即就业集中在中心城区而居民居住在外围，城市交通路线呈以市中心向外辐射的“轮毂”状(孙斌栋 等，2016)。随着交通技术进步，环城高速公路特别是地铁的建设，城市空间形态由单中心结构向多中心结构转变，即出现一个或多个城市副中心(subcenter)。本文将城市的“次城区”界定为城市副中心。具体来说，根据城市各市辖区到市中心的距离及人口密度，将城市“由内到外”分为中心城区、次城区和外围城区三个圈层。次城区是城市新要素集聚的形成场所，当中心城区过度集聚时会产生拥挤效应，导致人口、资本等要素向外扩散，由此在次城区形成新的集聚，也即城市副中心。城市副中心形成的过程，即是城市空间结构由单中心向多中心转化的过程。

基于前文式(30)～(32)中介作用模型，采用Poly代表城市的多中心度，测度如下：

Poly=P/N

(33)

其中，P表示i城市t年的“次城区”常住人口，N表示全市(所有市辖区)常住人口。该指标的含义是次城区人口比重，在一定程度上反映了地铁建设背景下城市空间结构的变迁。需要指出的是，这一指标不能体现职住均衡、就业分布(Lee，2007)或不同产业类型次中心(魏守华 等，2016)在多中心结构中的作用。本文关注的是次城区的相对人口规模，次城区相对人口规模越大，则城市的多中心发展程度越高。

(三)中介效应回归结果及分析

1.基准回归结果

表6汇报了基于式(31)、(32)的中介效应回归结果。列(1)、(2)验证了地铁建设通过扩张城市建成区面积影响人口增长率的机制，可以看到，地铁里程密度(ln Subway)和建成区面积占比(Area)的系数均显著为正,说明地铁建设促进城市建成区面积的扩张，进而为城市人口增长扩大了空间载体。由此，假说2得到支持。列(3)、(4)验证了地铁建设通过提高城市多中心程度影响人口增长率的机制，可以看到，地铁里程密度(ln Subway)和城市多中心程度(ln Poly)的系数均显著为正,说明地铁建设有助于次城区人口相对更快增长，推进城市空间结构向多中心形态演变，进而为城市人口增长提供更大动力。由此，假说3和4得到支持。

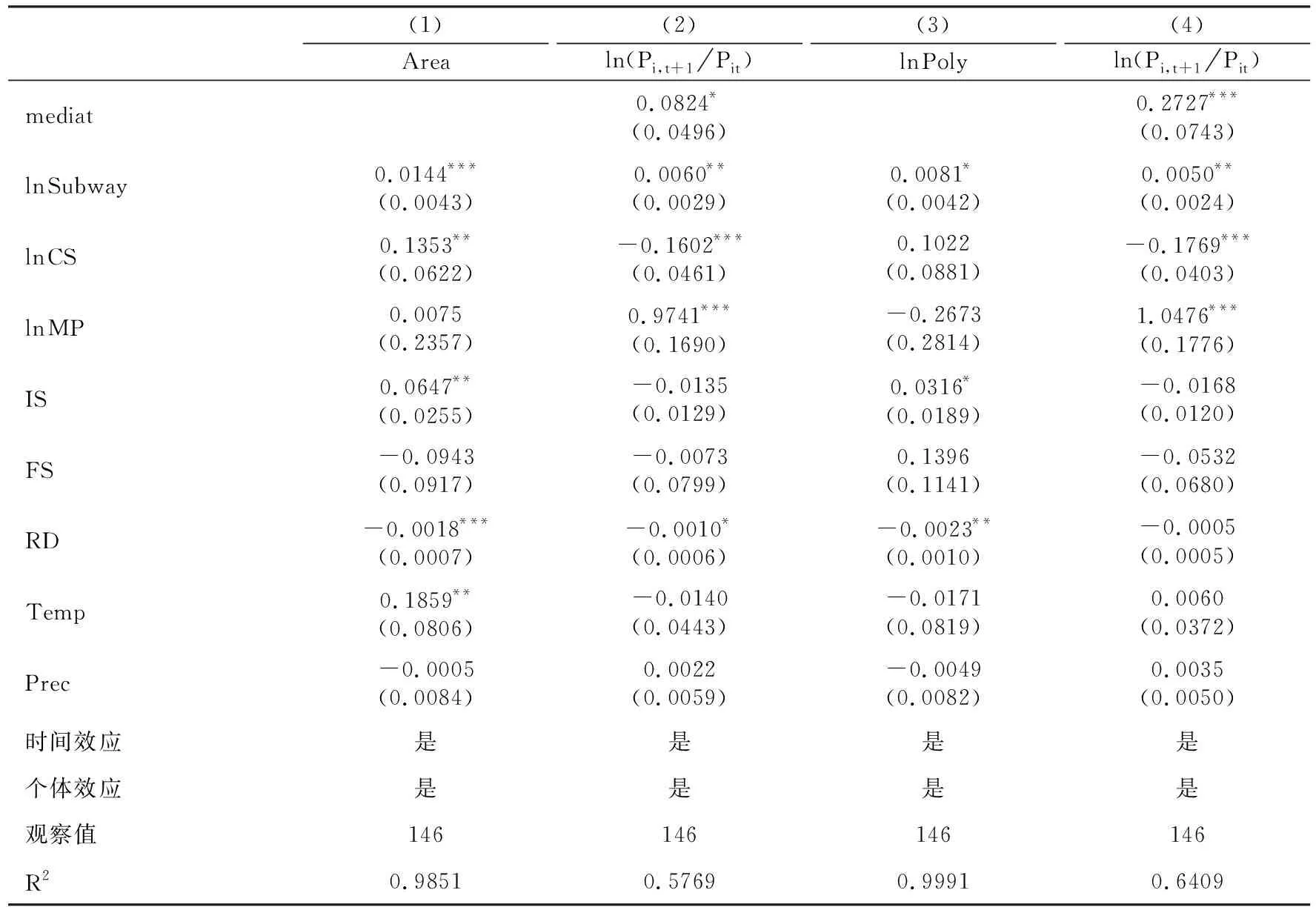
表6 中介效应模型的基准回归结果

交通基础设施改善促进了次城区的形成和建成区面积的扩张。交通基础设施的建设通常是从城市中心起步，逐渐向外扩散而形成网络，推动城市空间向外扩张，轨道交通尤其地铁的建设也是如此。城市中心在整体交通网络中处于核心地位，其可达性优于网络边缘的外围城区(周文通 等，2016)。次城区范围内的地铁线路与主城区联系紧密，通常能够形成纵横交错的线路网，居住在非城市中心的居民通勤成本降低，进而可以扩大城市半径。而由城市中心通往外围城区的地铁工程开通较晚，且线路单一，虽然有利于带动外围城区旅游业等产业的发展，但是由于人员流动成本更高，加之外围城区产业基础和配套设施较薄弱，因此相比于次城区，外围城区难以吸引本市居民迁入，也难以吸引其他城市的人口迁入定居。简言之，地铁建设以及因此形成的地铁网络强化了次城区的交通条件优势，助推了城市建成区面积的扩张，并带动了次城区的兴起，从而使得城市人口容纳规模提升，人口增长速度加快。

此外，地铁带动次城区发展、推动城市空间组织形式向多中心演进，还可能与地铁线形态有关。多横多纵的类“井”字形地铁线路强化了地铁站点之间的协同，扩大了地铁站点的服务范围。随着地铁建设的完善，这样的线路形态可能会逐渐出现在次城区，如广州地铁3号线南段，与8号线、4号线等线路交错合围，增强了番禺区的经济活力。放射状的地铁线路连接了大都市中心与近郊区地带，配合环线轨道，拓展了市中心的功能空间(龚锐 等，2019)，次城区居民将有更多的生活出行与工作通勤选择。

2.稳健性检验

沿用基准回归的思路，中介效应回归的稳健性包括以下两部分：

(1)将地铁站点密度(ln Station)作为核心解释变量。表7的列(1)、(2)显示，以建成区面积占比(Area)作为中介变量，地铁站点密度和建成区面积占比(Area)的系数均显著为正，说明建成区面积占比的中介效应仍然稳健；列(3)、(4)显示，以城市多中心程度(ln Poly)作为中介变量，地铁站点密度和城市多中心程度(ln Poly)的系数均显著为正，说明城市多中心程度的中介效应也是稳健的。总的来看，地铁站点密度相对地铁里程密度的系数较大，这可能与地铁站点数更能代表附近区域的可达性有关。

表7 中介效应稳健性检验：替换地铁度量指标

(2)筛选城市样本。在剔除2015年及之后开通地铁的城市的基础上，对中介效应进行稳健性检验，结果如表8所示。表8的列(1)、(2)显示，以建成区面积占比(Area)作为中介变量，地铁里程密度和建成区面积占比(Area)的系数均显著为正，说明建成区面积占比的中介效应仍然稳健；列(3)、(4)显示，以城市多中心程度(ln Poly)作为中介变量，地铁里程密度和多中心程度(ln Poly)的系数显著为正，说明城市多中心程度的中介效应也是稳健的。总的来看，地铁里程密度的系数稍微下降，这可能与地铁新近开通后几年内城市人口增长较快有关。

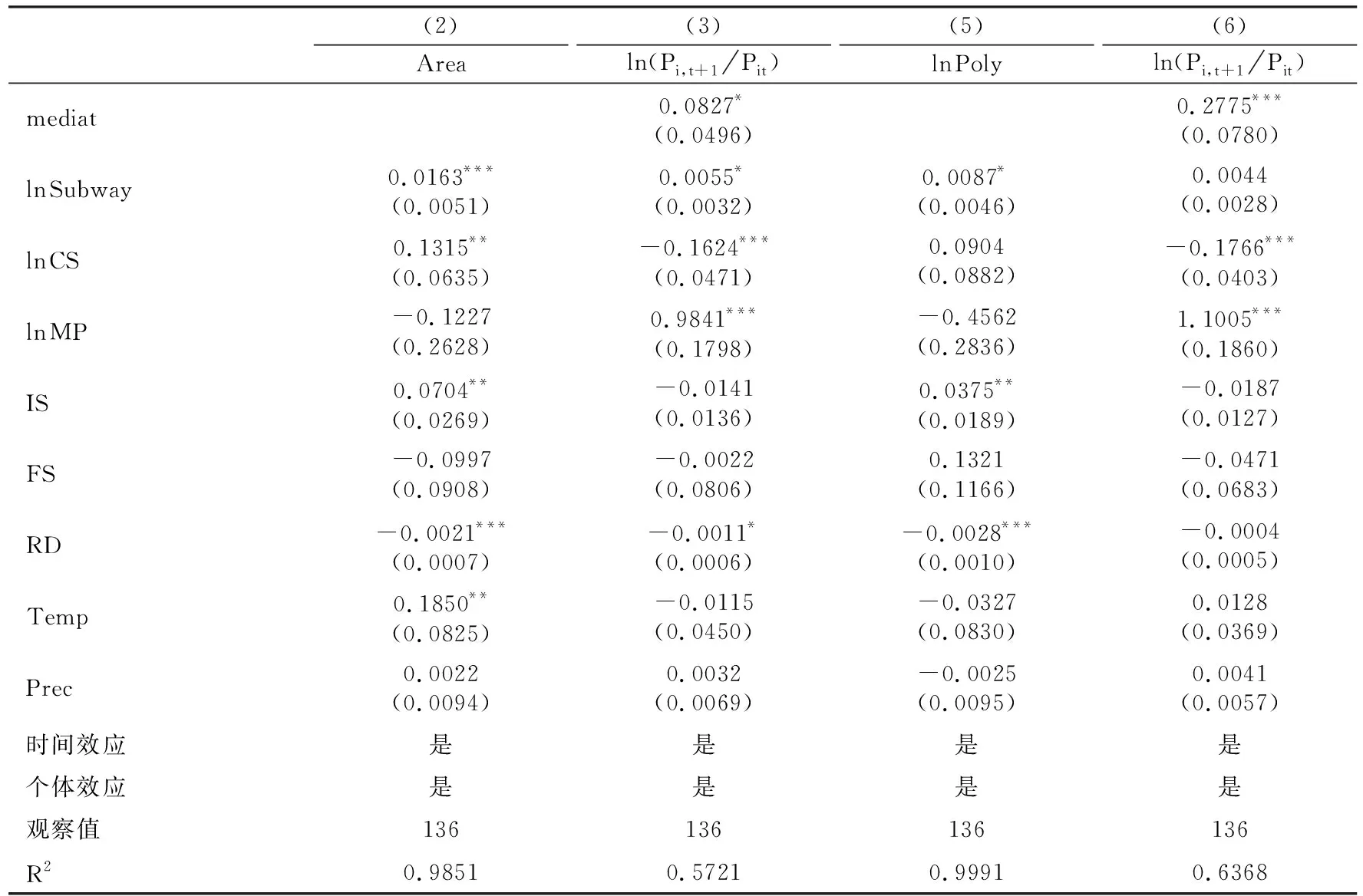
表8 中介效应稳健性检验：剔除部分样本

六、结论与政策含义

在理论模型分析的基础上，本文以地铁里程与站点密度衡量城市地铁建设水平，实证检验其对城市人口规模的影响；进一步，基于圈层结构划分出城市次城区并聚焦于其相对发展程度，构建新的指标测算城市的多中心水平，实证检验城市多中心结构在地铁建设促进人口规模增长中的中介效应。结果表明：城市地铁建设的推进对城市规模增长存在显著的正向作用，且这一作用部分是通过促进城市空间形态向多中心演变而实现的。地铁的扩张大大延展了人们的活动范围，经济活动不再局限于市中心，市中心集聚的拥挤效应得到疏解，在原本较为外围的区域形成了新的增长点，促进了市中心周边土地的开发利用，改善了城市外围的区位条件，增强了城市人口容纳能力。

本文的政策含义是：第一，应当进一步科学规划地铁建设，形成运行效率高、辐射范围大的地铁网络，并与城市道路相互配合，构建城市快速交通体系，提高城市内部各区位的可达性。第二，完善相关基础设施与配套服务，从而使得城市内部人员、产业等要素流通更便捷，增强城市的经济和人口承载能力。