一种Buck型DC-DC变换器的快速响应设计

张湘映，刘文政，赵 赟，李 旭，王德恒

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

近年来，采用数字方式控制的电源由于其可编程性以及可靠性等优势受到了市场的青睐。然而，数字控制方式相较传统模拟控制方式增加的模/数、数/模转换部分导致其系统难以企及模拟系统的及时性。因此，为使数字控制电源的优越性得到最大化彰显，本文以比例积分微分(PID)控制模块为基础，采用自适应PID、融入非线性思想的PID控制算法对其进行改进，从而提升系统的动态响应。通过这3种算法的对比，选择最适算法，并对其进行硬件实现。

1 Buck型DC-DC开关电源拓扑

Buck型DC-DC电路包括：主拓扑模块、模/数转换(ADC)模块、数字脉宽调制(DPWM)模块以及补偿模块构成。其中主拓扑模块如图1所示。

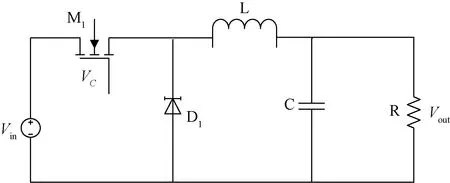
图1 Buck型DC-DC开关电源拓扑

其基本工作原理如下：

当作用于开关管M的驱动信号使其导通时，二极管 D反偏，此时该路不导通。该模式下负载R两端的电压由电源提供，此时电感的电压电流表现为如下关系：

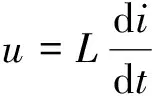
(1)

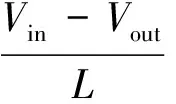
当开关管M表现为截止状态时，续流二极管D正偏呈导通态，电感能量借助其传送至负载R，同时当作用于负载R的压降小于电容C的压降时，电容C亦向负载R传送能量。

系统在平衡状态下，忽略器件内阻等因素时的负载输出电压为：

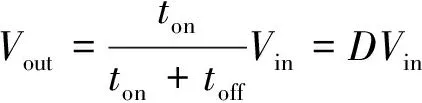
(2)

式中：恒小于1，即恒小于，因此Buck型开关拓扑也可称为降压式开关电路。

2 数字DC-DC电路的设计与验证

2.1 基于原始PID控制的数字DC-DC电路的设计与验证

Matlab/Simulink平台搭建的Buck型DC-DC电路模型如图2所示。其模型由主拓扑模块、ADC模块、DPWM模块以及补偿反馈模块组成。

图2 数字PID控制的Buck型DC-DC电路的Matlab/Simulink模型

PID模块编写的核心为PID补偿器的公式：

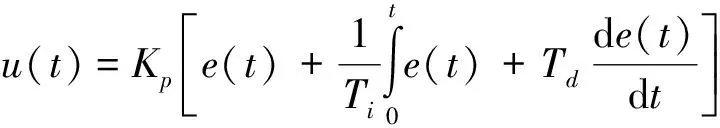
(3)

本次搭建模型的采样时间设置为1 μs；输出电压取值为(1)×1 000；PID补偿器的公式中误差信号表示为-，定义为参考电压值相较实际输出电压值的差值。

图3为PID补偿系统的原理框图，其利用实际输出的电压值与基准值的差值通过PID运算生成控制量()，从而实现对被控量的控制。理想情况下连续时间PID控制器可用下式表示：

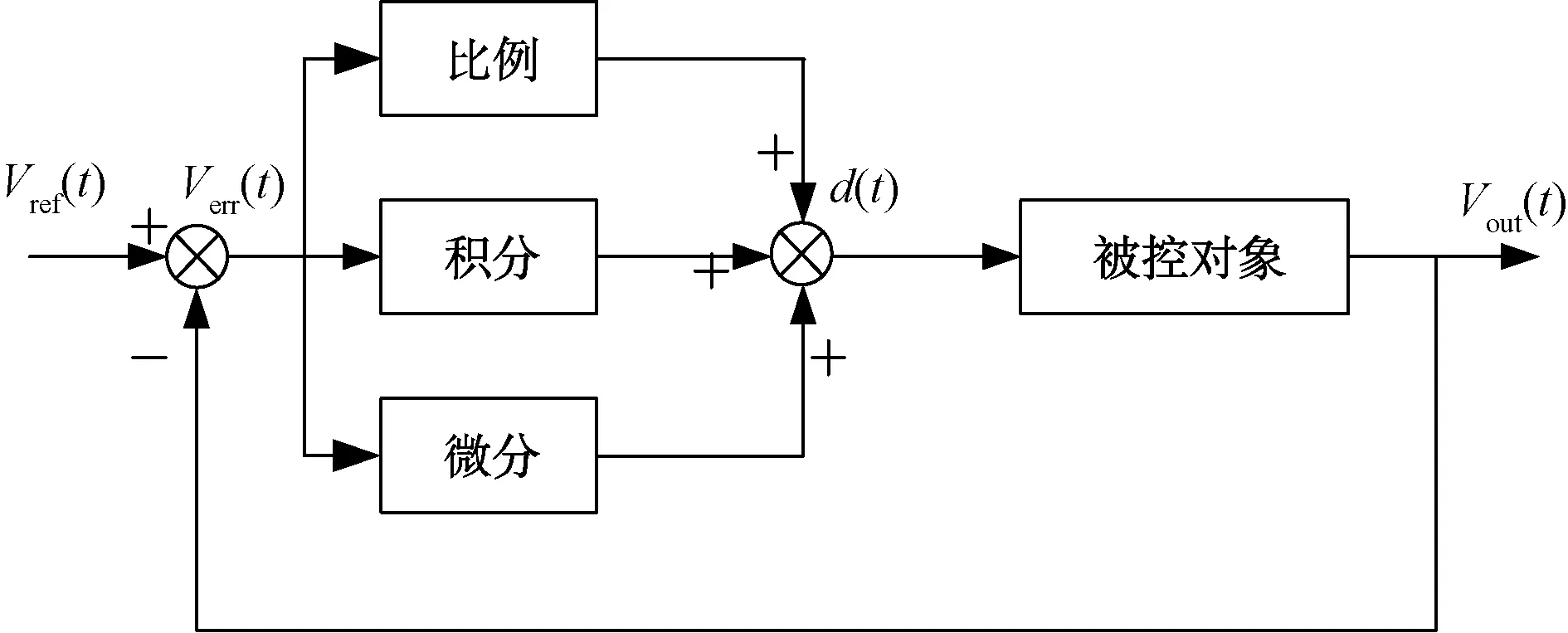
图3 PID控制系统原理框图

(4)

式中：为比例系数；、分别表示积分、微分时间常数；()为实际输出信号与参考信号的差值。

2.2 引入自适应的PID控制

自适应PID的控制方程为：

()=(-1)+(+)[()-(-1)]+

(+)()+(+)[()-

2(-1)+(-2)]

(5)

式中：、、稳态时的值为0；瞬态时这三者的值由2.1节所述误差信号决定。

、、的值随误差信号的改变而自适应地变化。图4为其实现的原理框图。

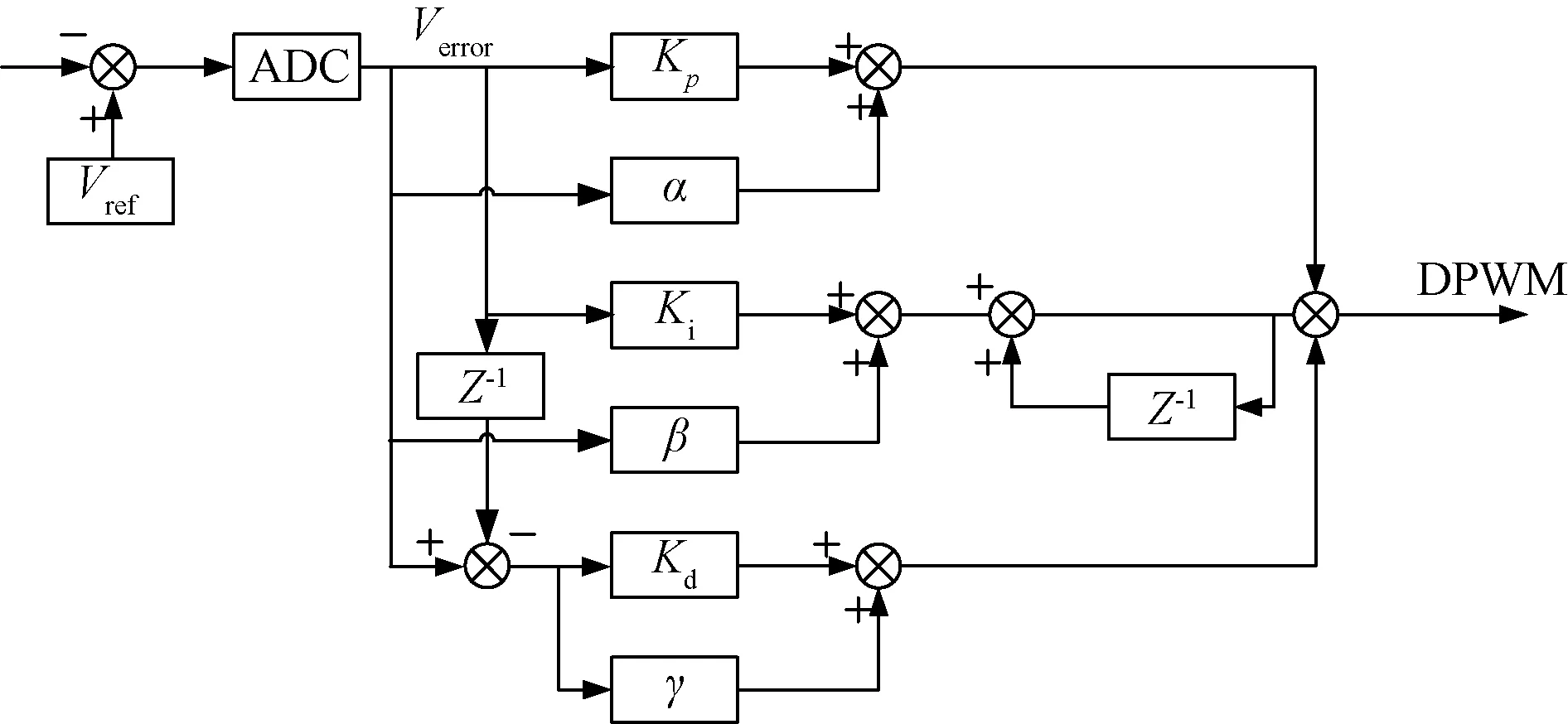
图4 自适应PID补偿器框图

、、3个参数值的判定公式如下：

(6)

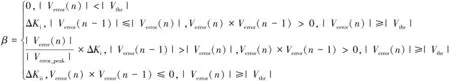
(7)

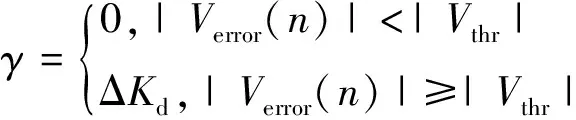
(8)

式中：|()|表示当前状态下误差信号的绝对值；||表示阈值电压的绝对值；||表示误差电压的峰值的绝对值；Δ、Δ分别表示上升沿瞬态时、的值;Δ、Δ分别表示过渡瞬态时，的值;Δ表示过渡瞬态、上升沿瞬态时的值。

2.3 基于改进PID控制的数字DC-DC电路的设计与验证

fal函数是对“大误差，小增益；小误差，大增益”的数学拟合，它具有快速收敛性，因此是一种常见的非线性反馈结构，兼具良好的鲁棒性和适应性。其表达式如下：

(9)

式中：表示线性区间段的长度；可理解为fal函数的非线性度，其值取0～1间的某一常数；表示输入误差。

结合fal函数后的PID控制器的形式如下：

=fal(,,)+

fal(,,)+fal(,,)

(10)

式中：为误差信号；、、分别为PID控制模块的各增益参数。

其控制器结构图及其对应电路框图如图5、图6所示。

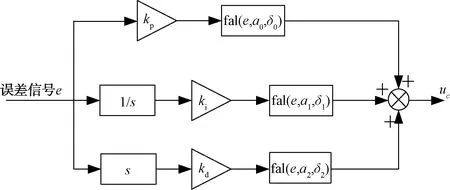
图5 fal-PID控制器结构图

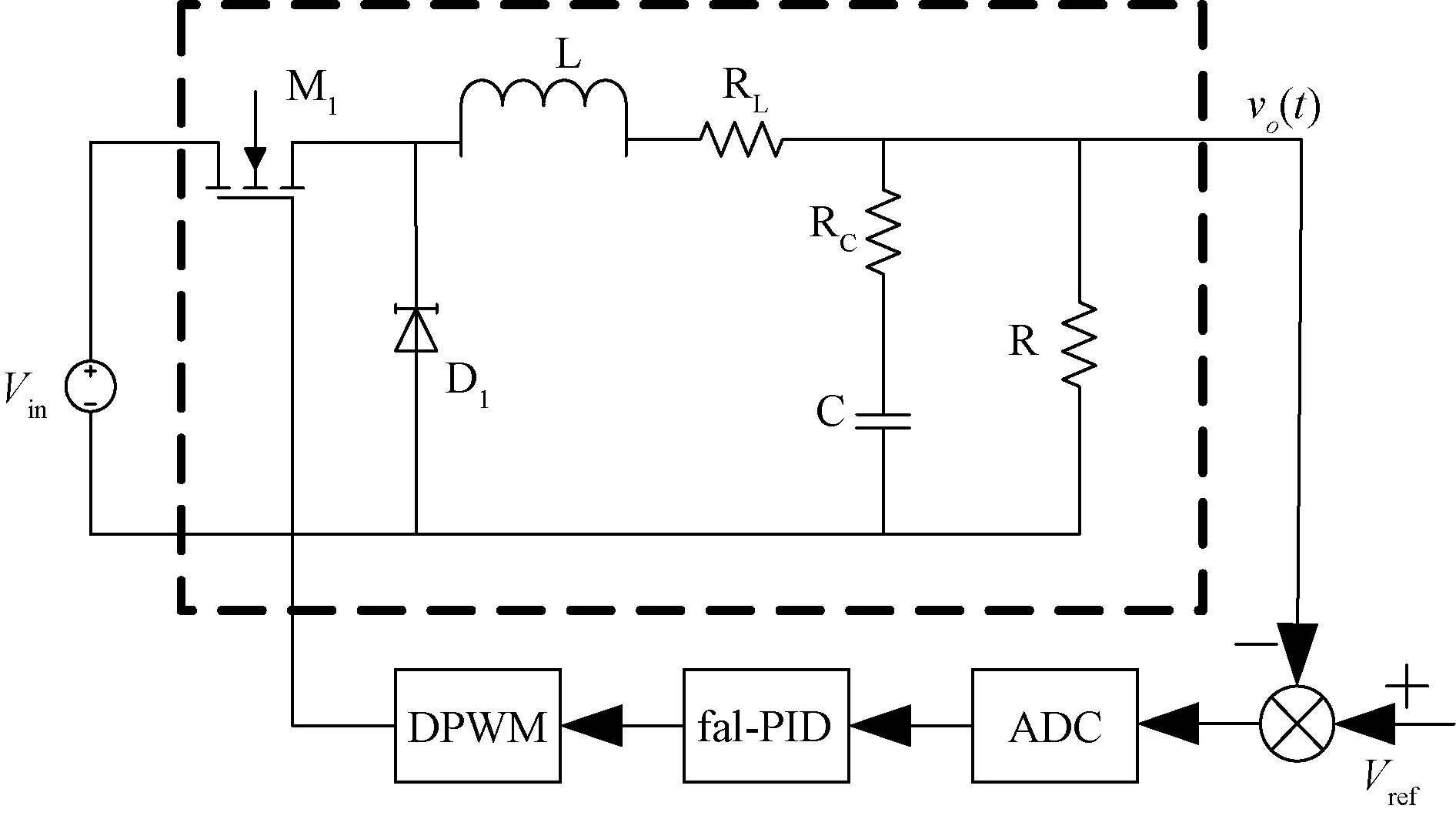
图6 fal-PID控制电路框图

2.4 3种PID控制的数字DC-DC电路的仿真结果对比

图7～图9所示分别为基础PID、引入自适应思想的PID、引入fal后函数的PID对应电路在负载突变时的输出电压曲线。为便于比较，设置统一的仿真时间6 ms，在5 ms时，负载电流由0.12 mA突变为0.24 mA。

图7 基础PID负载突变的输出电压曲线图

图8 自适应PID负载突变的输出电压曲线图

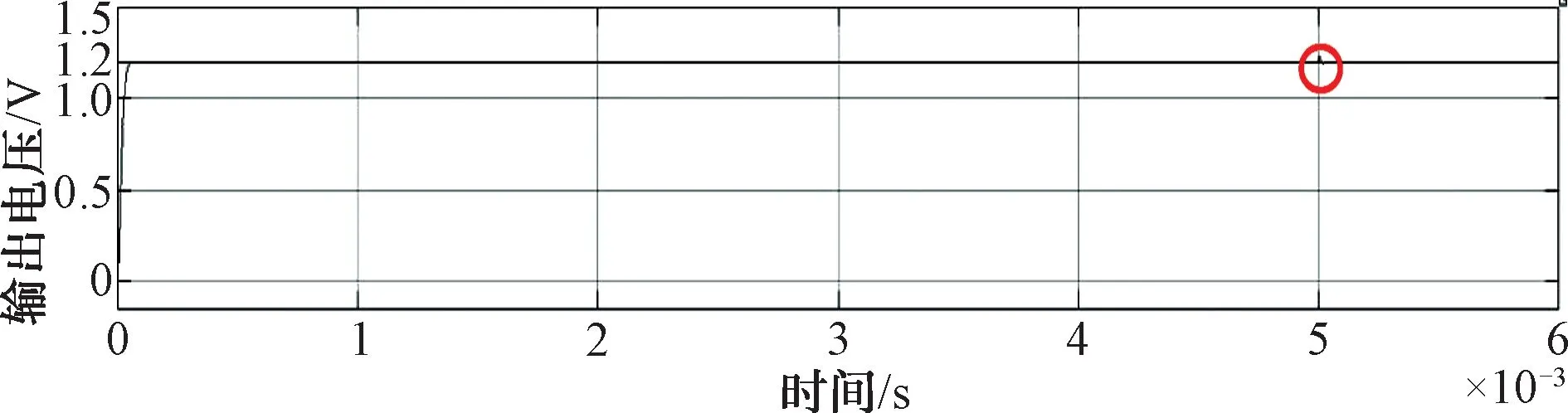
图9 引入fal函数的PID负载突变的输出电压曲线图

综合所得输出曲线图的结果，结合了fal函数这一非线性控制方法的PID控制器具有简便、构造效率高等众多优点，且其输出能达到更佳的动态性能。同时，与2.2节所述自适应PID结构相比，算法上更加简洁，而其结果也更佳。

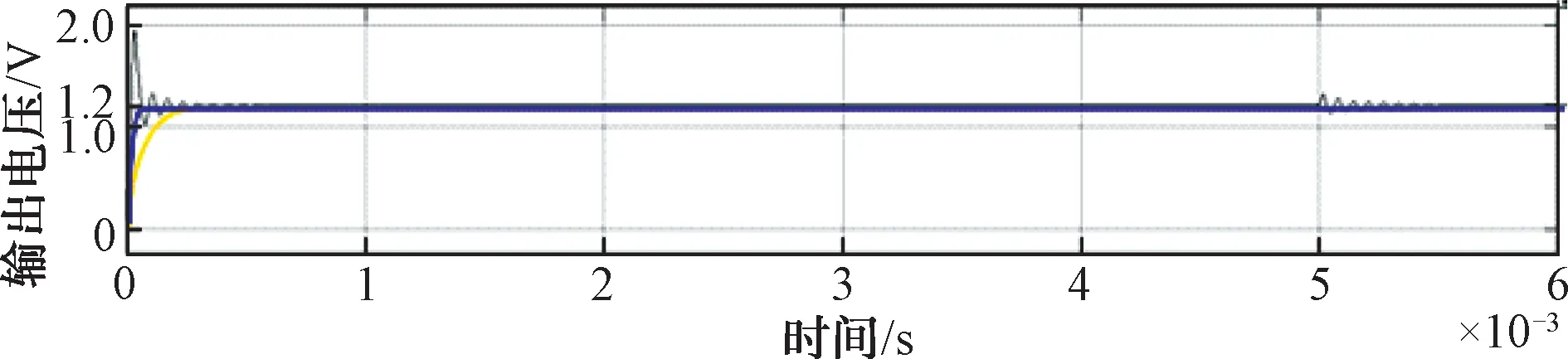
图10 3种输出电压曲线图对比

为更加直观地观察自适应PID与引入fal的PID在负载突变时的输出结果，取5～6 ms这一区间，将图8和图9在5 ms负载突变时(即图中圈出部分)的结果放大，如图11和图12所示。

图11 自适应PID负载突变的输出电压放大曲线图

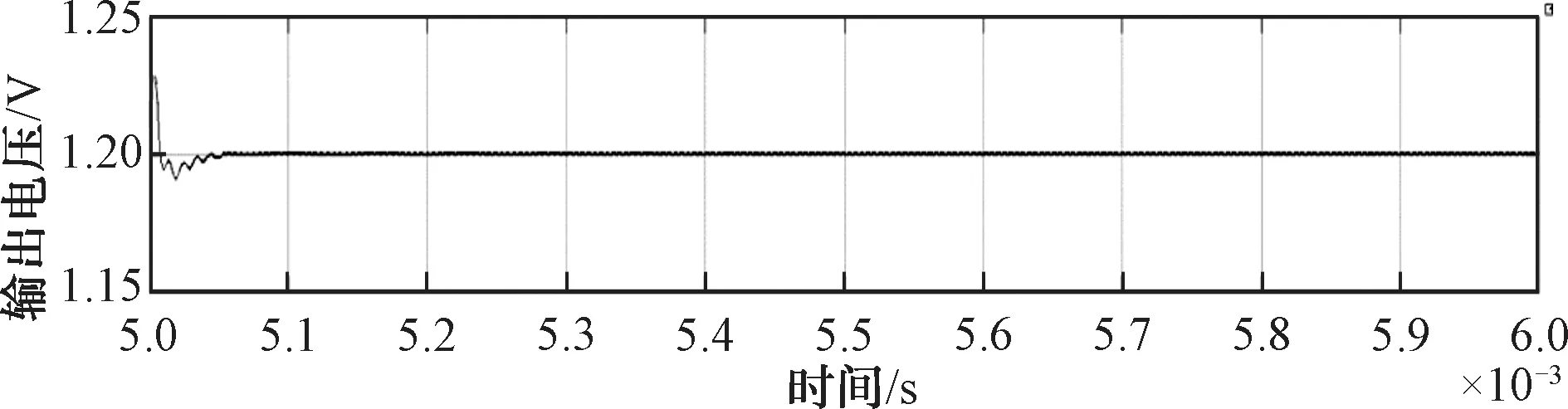
图12 引入fal函数的PID负载突变的输出电压放大曲线图

表1将这3种PID控制下的输出电压的主要指标进行了对比。由表格内容可见，相较前2种算法，fal-PID控制在系统启动时的响应时间分别缩短了50%和33%，在负载突变时的响应时间分别缩短了78%和50%。

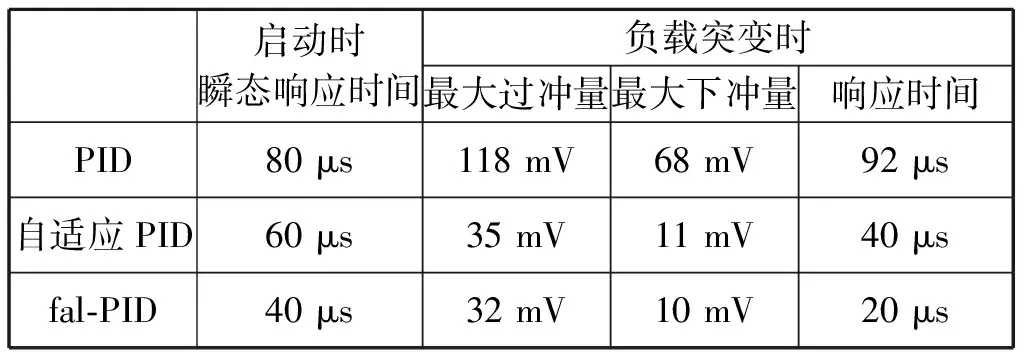
表1 3种PID算法对应输出电压主要指标

3 Buck型DC-DC电路在FPGA上的实现

本次测试的输入电压设为5V，期望的输出电压为1.8 V。得到的输出结果如图13所示。

图13 示波器输出电压

为研究其负载突变时的动态响应性能，在某一时刻将原10 Ω电阻突变为5 Ω，并在另一时刻再突变为10 Ω，其对应输出波形如图14所示。

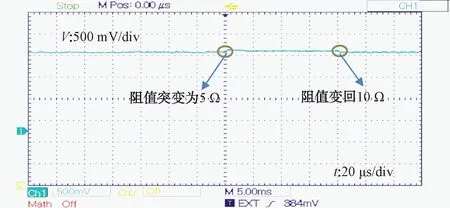
图14 负载突变波形

如图14所示波形，电阻在突变为5 Ω以及突变回原始阻值时，都表现出了良好的动态响应性能。在某时刻对其负载进行改变时，负载电流由100 mA增至300 mA，对应的正负电压阶跃最大仅为80 mV左右，约为输出电压值的4.7%，其瞬态响应时间也仅为150 μs左右，负载调整率为40 μV/mA。本次实验结果基本符合预期。

4 结束语

本文对Buck型DC-DC电路进行了介绍，并就其中的动态响应性能进行分析。为进一步验证，基于Simulink平台对Buck型开关变换器的各模块进行搭建、仿真，并针对输出电压的动态性能就PID模块进行改进并进行系统仿真，对比改进前后的输出电压波形，验证改进后的系统具有更佳的动态响应性能。最后，基于现场可编程门阵列(FPGA)平台对其中最优算法的Buck型开关变换器进行搭建，并进行了硬件实测验证。