基于概率密度的面源刻度法对碘盒中131I 的定量监测
许 丰 王所富 郭建友 於国兵 徐 平 王雪建
1(安徽大学物理与光电工程学院 合肥 230601)
2(安徽大学物质科学与信息技术研究院 合肥 230601)
3(安徽省生态环境保护厅辐射环境监督站 合肥 230071)
4(中国科学技术大学核科学技术学院 合肥 230027)
碘的放射性同位素有125I、129I和131I,环境中气态放射性碘的监测主要针对核设施中释放的131I[1-3]。131I是一种气态放射性核素,吸入后主要趋向于甲状腺照射,是核设施气态流出物监测的重点项目[4-6]。环境中131I的监测有两种方法:一是采用监测仪进行实时监测;二是使用碘采样器采样后对碘盒进行γ 能谱测量。γ 能谱测量方法逐渐在监测领域成为常用手段,因此探测器对碘盒中131I 的探测效率刻度是影响定量监测准确度的关键因素。碘盒取样131I 的探测效率需专门制作131I标准源来刻度,但131I 半衰期短(T1/2=8.025 2 d),易挥发,不宜用作长期标准源,并且制作此源也比较困难。因而探索一种简易估算131I γ 总探测效率的方法很有意义。
气态131I 在含活性炭介质的碘盒中,一般会沿着深度方向呈非均匀分布的形态[7],如果将非均匀分布的体源当作均匀分布的体源进行测量,会产生很大的误差[8]。因此,为了实现对碘盒中131I的定量监测,需要建立不均匀分布的碘盒体源测量模型。国内外学者对碘盒不均匀分布的情况进行了大量的研究,如用133Ba 点源[9-10]或133Ba 面源[11-13]代替131I加权积分以及131I点源直接估算碘盒中体源探测效率的方法[14],虽然对碘盒体源的制作方法的改进有一定的意义,但是采用点源、面源加权积分去计算非均匀碘盒体源的探测效率过程繁复,且并未讨论气态碘在碘盒中的分布系数问题;还有学者通过蒙特卡罗方法对碘盒分层模拟计算实现了特定分布系数下的碘盒体源探测效率[15]或者求解病态矩阵方程等数值推导得出特定深度分布情况下的探测效率[16-17],虽然研究了分布系数对非均匀分布碘盒的探测效率的影响,但是并未解决实际样品的分布系数求解与相关探测效率标定。综上所述,如果能直接根据获得的碘盒样品内的分布系数对气态碘进行定量计算将具有十分重要的意义性。
本文提出了一种基于概率密度的面源效率刻度方法,解决了碘盒体源的分布系数求解和探测效率标定的问题。通过该刻度方法对正反放置下探测效率或者计数率的比值与分布系数α进行函数拟合,得到了适用于标定碘盒体源分布系数的相关经验公式。只需通过简单的正反放置下的能谱分析,即可求出气态碘在碘盒中的分布系数,然后结合有源、无源或者有源-无源联合测量的手段进行探测效率计算,实现碘盒中131I的定量监测。
1 方法原理
基于蒙特卡罗方法模拟131I 面源,假定将含活性炭介质的碘盒切割成多个等间隔高度区域,面源放置在不同高度区域上测量其γ射线特征峰的探测效率εdisk,通过对探测效率εdisk与样品高度h最小二乘法拟合得到函数关系εdisk(h),具体测量模型如图1所示。
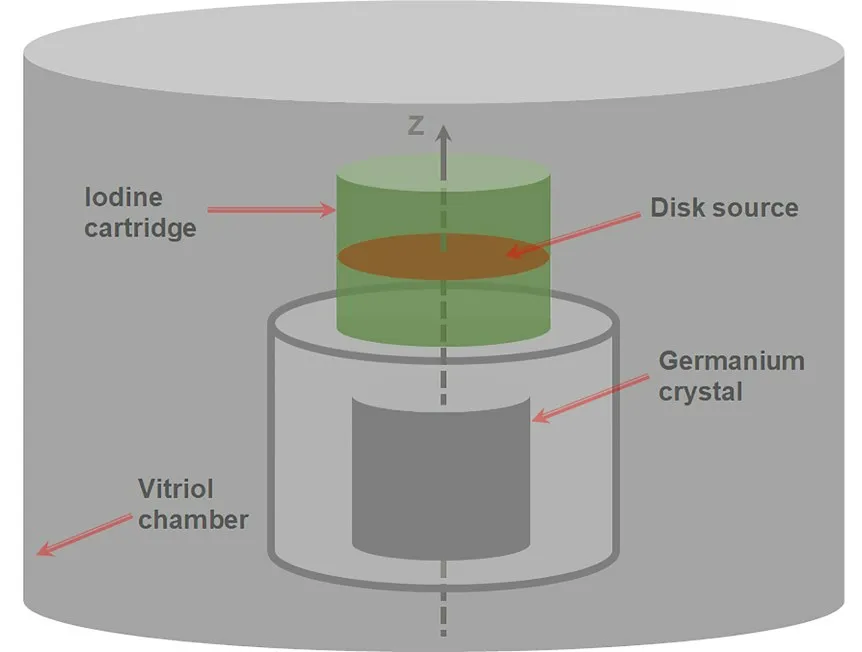
图1 面源对碘盒内气态碘效率计算模型的示意图Fig.1 Schematic diagram of the calculation model of gaseous iodine efficiency in iodine cartridge by disk source pair
同时由于气态碘在碘盒中是非均匀分布的,一般呈现负指数分布的形态,引入一个概率密度函数λ(h),λ(h)= e-αh,α为分布系数。因此探测器对于整个非均匀分布的碘盒样品的探测效率εV可以表示为式(1)。
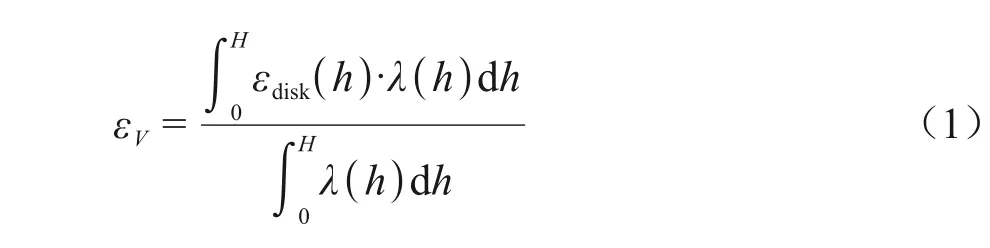
对于式(1)物理含义的解释:放射性核素沿深度方向呈现概率密度分布时,体源探测效率等于均匀分布情况下面源效率函数εdisk(h)乘以概率密度函数λ(h),并对深度积分归一化处理的结果。然后假设将碘盒反向放置,则其概率密度函数为λ'(h),通过数学分析可知,λ'(h)=Ceαh,C为反向放置的概率密度函数的常数项。因此探测器对于碘盒反向放置样品的探测效率ε'V可以表示为式(2)。

因此通过数值计算,可以获得对于碘盒正反放置时,不同指数系数下的131I γ 核素的各射线峰的探测效率值。在实际测量时,即使知道不同分布系数下的探测效率,对于实际分布系数目前仍是无法求解的。因此为求解碘盒体源的分布系数,本文引入指数系数因子K,该因子是正反放置下探测效率的比值,是获取气态碘在碘盒中实际探测效率的关键参数。具体数学表达如式(3)。

2 结果与分析
2.1 概率密度面源刻度方法对碘盒正反放置效率计算
本文采用基于蒙特卡罗方法开发的无源效率刻度软件LabSOCS 进行探测效率的模拟计算,该软件是由法国Canberra 公司与美国Los Alamos 国家实验室共同开发的产品,相关学者或机构将该软件与传统的有源效率刻度技术进行对比研究,结论表明该软件分析结果与传统方法分析结果一致[18-20]。具体表征探测器为实验室型号BE5030(Ultra-Low-Background)γ 谱仪系统(该探测器晶体尺寸为φ80.5 mm×31.0 mm,相对探测效率为47.3%,多道脉冲分析器(Lynx)为Canberra 生产)。假定将TC45 型号碘盒分成多个等间隔高度的区域,高度间隔为0.2 cm。面源分别置于不同高度区域上测量其探测效率,计算结果如图2所示。
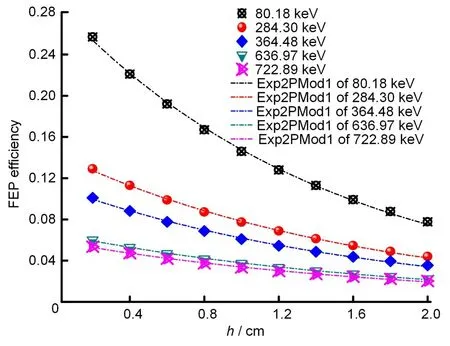
图2 碘盒内部不同高度面源的模拟计算结果(彩色见网络版)Fig.2 Simulation results of disk sources at different heights inside iodine cartridge(color online)
对图2中131I的5条γ射线峰的探测效率利用计算结果进行最小二乘法拟合,采用指数函数拟合公式,具体表达式为εdisk(h)=A·exp(B·h)。式中,A、B为拟合参数,详细拟合参数值及拟合优度R2如表1所示。
通过表1中拟合得到的具体参数进行气态碘指数形式活度分布相关系数的计算。假定指数分布系数α的取值范围为0~10.0,依据是对于指数系数趋向于0,其核素的张驰深度为无限大,此时其核素在2 cm 活性炭中的分布趋向于均匀分布。而对于指数系数为10.0,其张驰深度为1 mm,此时核素分布于活性炭-采样器一面的活性炭表层,此时等效为面源。当指数系数大于10.0 的情况,在实际采样过程中属于罕见情形,不做讨论。因此,对指数系数αϵ(0,10.0),分别选取0.1、0.2、…、1.0;1.1、1.2、…、1.5;2.0、4.0、…、10.0。利用式(1)对碘盒正向放置的探测效率进行计算,将计算结果整理如表2 所示。

表1 碘盒内部面源与高度的函数拟合参数Table 1 Function fitting of internal disk source and height of iodine cartridge
表2已经对正向放置条件下碘盒体源的探测效率进行了计算,参照表2中的指数分布系数,对反向放置条件下的碘盒探测效率进行求解。反向放置的探测效率求解首先是确定一个合理且易于计算的概率密度函数。这里取反向放置的概率密度函数形式为λ'(h)=Ceαh,为证明该函数关系具有良好的拟合效果,选取α=1进行正反放置下的概率密度函数的拟合效果对比研究,如图3(a)所示,不同指数系数条件下对应的反向放置的概率密度函数的常数项C的拟合关系如图3(b)所示。

表2 碘盒正向放置时不同能量的探测效率计算结果Table 2 Calculation results of detection efficiency of different energies when iodine cartridge is placed forward
通过图3可以看出,反向放置下选取的概率密度函数对选取点的拟合结果与实际取值吻合,验证了反向放置下的概率密度函数的可靠性。同时对于任意分布系数α,可以利用图3(b)对反向放置下的概率密度函数的常数项C求解,该关系式可用于碘盒反向放置时进行碘盒的体源探测效率计算。因此根据上述关于碘盒反向放置下的概率密度函数的分析,可以结合式(2)对反向放置条件下的碘盒体源的探测效率进行计算,分布系数的选取同表2,最后将反向放置的探测效率计算结果整理如表3所示。
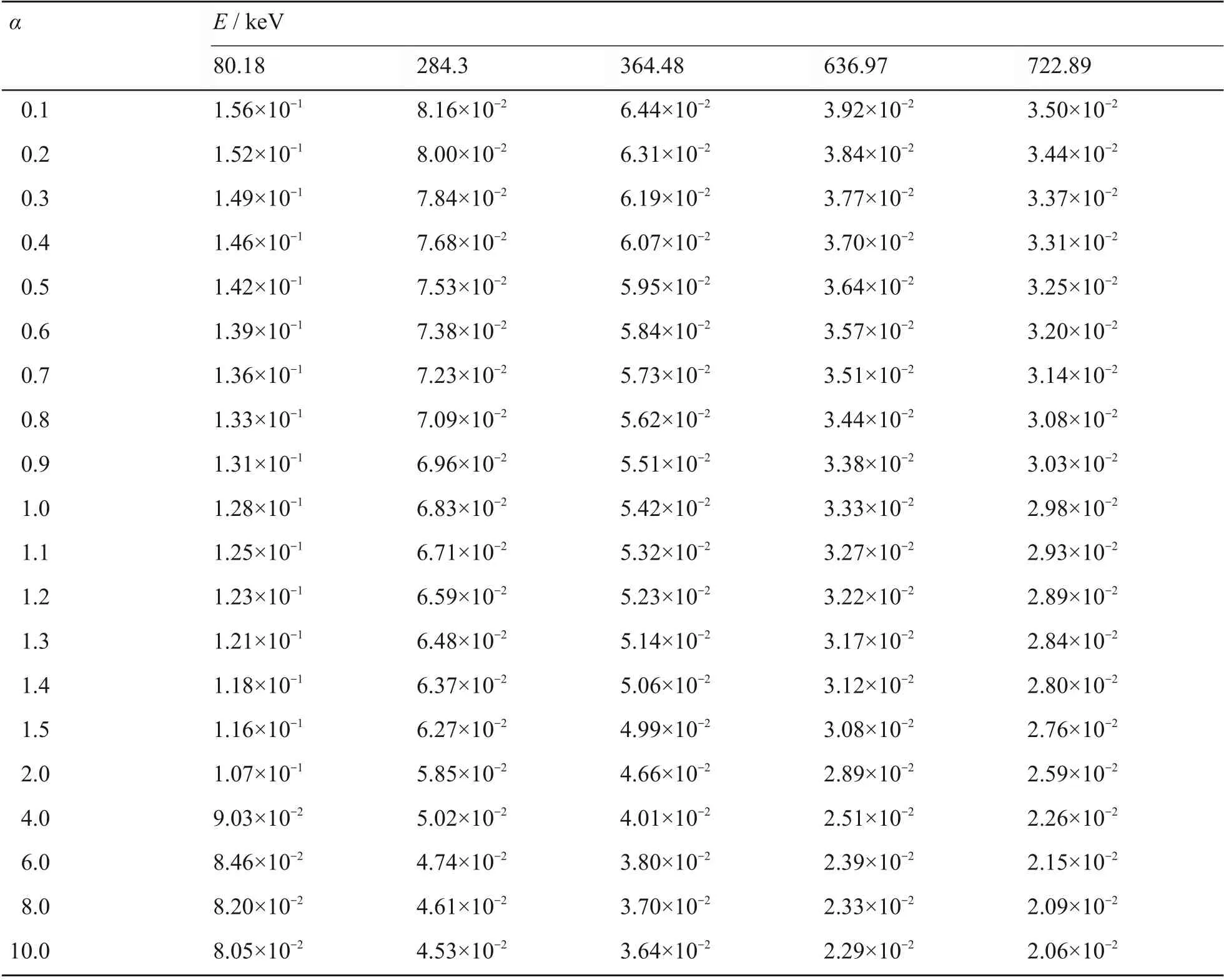
表3 碘盒反向放置时不同能量的探测效率计算结果Table 3 Calculation results of detection efficiency of different energies when iodine cartridge is placed reverse

图3 碘盒内气态131I正(a)反(b)向放置下分布函数比较Fig.3 Comparison of distribution functions of gaseous131I in iodine cartridge in positive(a)and negative(b)direction
2.2 碘盒内气态碘分布系数标定公式提出
通过表2、3 对正反放置下的探测效率的计算结果,可以得到不同分布系数情况下的碘盒正反放置的探测效率比值,即指数系数因子K,具体计算过程参照式(1)~(3)对指数系数因子K进行求解,然后根据正反放置时得到的指数因子K与分布系数α对应关系进行数值分析。指数因子K与分布系数α对应关系如图4所示。

图4 指数系数因子K与分布系数α的关系Fig.4 Relationship between exponential coefficient factor K and coefficient α
通过图4可以看出,指数系数因子K随着分布系数α逐渐增大,射线之间由于不同能量而导致的自吸收效应不同,探测效率之间有所差异。因此,虽然变化规律基本一致,但是最终得到的指数系数因子K对分布系数α的灵敏性不同。根据图4中131I的所有特征γ射线峰所表征的α-K关系进行最小二乘法拟合,选取的函数形式表达式为α=m·exp(K/t1)+n·exp(K/t2)+P。式中:m、n、t1、t2、P为拟合参数,拟合得到的详细参数值和拟合优度R2如表4所示。

表4 指数系数因子K与指数系数α的函数拟合参数Table 4 Function fitting parameters of exponential coefficient factor K and exponential coefficient α
2.3 实验验证
为验证上述方法得到的经验公式在实际工作的可靠性,采用北京华瑞核安科技公司生产制造的HH02-IS42 型碘采样器(仪器参数:重量7.6 kg;规格1.8~7.2 m3/h;额定电压AC220 V;额定功率160 W;准确度±2.5%)对气态碘进行采样,碘盒型号TC45。采样得到多组样品,编号#1、#2、#3、#4 和#5,然后利用实验室型号BE5030(Ultra-Low-Background)γ 谱仪系统对样品进行测量,实际气态碘采样环境布置如图5(a)所示。在实验分析中选取特征峰364.48 keV 去计算碘盒中131I探测效率及放射性活度,主要是由于131I的虽然有5个能量峰,但是364.48 keV的发射强度高度81.5%,远高于其余4 个能量峰的发射强度(80.18 keV、284.3 keV、636.97 keV、722.89 keV的发射强度分别为7.16%、 6.12%、 2.62%、1.77%)。核应急等场所面临短时间测量或日常辐射监测遇到的活度较低等情况,选取该射线分析气态碘放射性的计数统计误差最小。根据表4中拟合的经验参数和式(4)对实际样品中分布系数α进行计算,然后通过概率密度的面源刻度方法求解特征峰364.48 keV的探测效率。为对比验证方法的可靠性,采用拆解-搅拌-回填的手段实现均匀碘盒源测量,具体流程是首先对碘盒进行拆解,然后转移至纸杯中搅拌均匀,最后装回原碘盒中封装。均匀样品在实验室常常采用相对比较法[21]进行计算处理,碘盒拆解前后如图5(b)所示。

图5 碘采样现场布置图(a)及碘盒样品处理(b)Fig.5 Iodine sampling site layout(a)and iodine cartridge sample processing(b)
为反映碘盒直接测量的不均匀性导致的计数差异性和拆解-搅拌-回填方法处理不均匀碘盒的效果,选取编号为#1 的碘盒样品,对正反放置下直接测量得到的γ 能谱,和拆解-搅拌-回填后样品正反放置下测量的γ 能谱进行分析,测量时间均为60 s。具体能谱前后测试及对比情况如图6所示。

图6 编号#1样品能谱测试前(a)后(b)对比(彩色见网络版)Fig.6 Comparison of energy spectra of sample No.#1 before(a)and after(b)test(color online)
通过图6(a)可以看出,对于不均匀分布的碘盒体源直接进行测量,正反放置情况下的计数差异比较大,具体表现为对于γ 射线特征峰364.48 keV,直接测量选取的#1样品的正反计数偏差高达59.84%,如果视作均匀体源计算时不可避免会引起较大的偏差,因此本文涉及的方法对于碘盒非破坏性直接测量具有十分重要的意义。而通过图6(b)可以看出,在反复搅拌后,碘盒正反放置的计数趋于一致,说明经过拆解-搅拌-回填后样品均匀性较好,作为对照组满足均匀体源的测量要求,因此对其余几组样品采用相同的方法进行处理。然后分别对采集的气态碘131I 进行计数率计算,同时结合表4 的拟合参数和式(4)对分布系数α进行计算,样品的计数率与分布系数α的计算结果如表5所示。
通过表5 可以看出,测试的碘盒样品直接测量所得到的计数率偏差较大,具体计数率偏差:编号#1~#5 的正反放置计数率偏差分别是59.84%、60.84%、62.70%、62.32%和60.76%,因此,如果将样品视作均匀体源处理,将会造成极大的偏差,同时也可以看出,偏差与分布系数是正相关的。根据直接测量得到的正反放置下计数率的比例关系,对131I 的364.5 keV 的射线峰开展分布系数计算,然后结合式(1)或式(2)计算364.5 keV 的射线峰所对应的探测效率。同时根据表5,也可以看出,拆解-搅拌-回填的手段获得的对照组均匀性良好,可以视作均匀体源去计算分析,搅拌后的正反放置的具体计数率偏差为:编号#1~#5的正反放置计数偏差0.5%、2.2%、1%、2.3%和1.9%。最后根据上述分析,对碘盒内气态131I 的放射性活度进行计算处理,活度计算过程中选取的特征γ射线能量为364.48 keV,体源的活度计算方法为:Am=n/(FεQ),n该γ 特征射线峰的计数率,单位为s−1;F为γ 射线发射强度;Q为衰变修正因子;Am为样品活度,单位为Bq;ε为体源探测效率。将具体的计算结果整理如表6所示。

表5 实验样品γ射线峰计数率及分布系数α计算结果Table 5 Calculation results of γ-ray peak counting rate and distribution coefficient α of the experimental sample
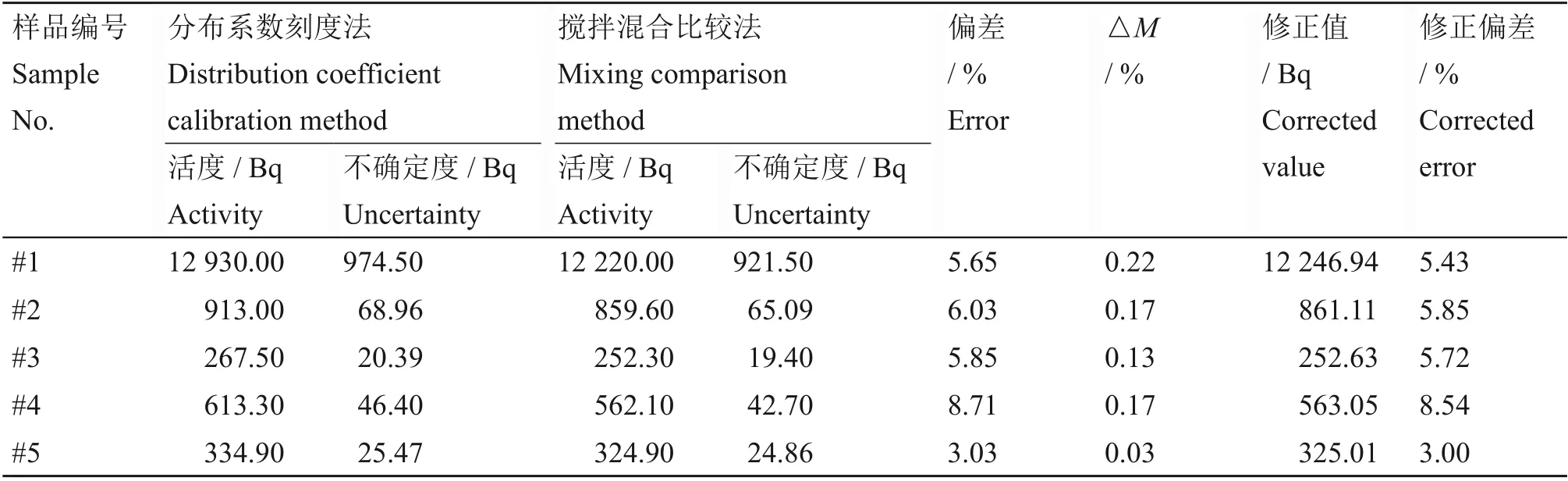
表6 概率密度面源积分法对131I活度计算结果与搅拌均匀后计算结果比较Table 6 Calculation results of131I activity by using the probability density surface source integration method are compared with that by mixing evenly
通过表6可以看出,基于概率密度的面源刻度方法得到的活度值与搅拌混合均匀后的活度值较为一致,同时在回填过程中碘盒中活性炭颗粒的损失率也比较小,实际损失率不高于1%。通过碘盒拆解回填过程中的损失率校正,对修正后的活度值可以看出,编号#1~#5的样品活度值相对偏差为5.43%、5.85%、5.72%、8.54%和3.00%,两种方法得到的活度值之间偏差均小于10%[5],结果大体一致,表明了该方法的可行性。今后在实际测量工作中可依据概率密度的面源刻度方法对碘盒内活性炭颗粒吸附的气态131I 进行计算,由于是对碘盒样品内射线的指数系数因子K的比例计算,即使采用上述研究的技术成果,在其他探测系统上进行能谱测量及计算也是可保证结果的可靠性的[22]。同时,实验为节省时间而基于蒙特卡罗方法进行模拟计算的获取的经验公式,在今后可以通过有源效率刻度技术或者有源-无源联合测量方法,将会得到更好的效果。
3 结论
本文通过提出概率密度的面源刻度方法对碘盒中吸附的气态131I 进行定量监测分析,通过碘盒的正反放置获得的计数率比值,即指数系数因子K,标定气态碘在碘盒中的分布系数α,然后利用分布系数α得到不均匀分布碘盒体源的探测效率。实验上通过获得的碘盒样品直接正反放置测量,结合概率密度的面源刻度方法,计算选取的特征γ射线峰364.5 keV 的指数因子K,利用K-α关系计算碘盒样品的总活度。结果表明上述方法对实验样品直接正反放置测量计算结果与后处理得到的均匀体源活度计算结果相比,均匀偏差为5.71%。实验结果验证了概率密度面源刻度方法在碘盒测量工作中的可靠性,为实现气态碘的定量监测提供一条可行的途径。对非均匀性样品源进行非破坏性分析一直以来都是监测热门方向,本研究成果对与碘吸附过程类似的样品源定量监测也有一定的借鉴意义,如氡气的吸附采样,一般在活性炭介质表面的浓度最大,越到炭床深处氡浓度越低[23]。
作者贡献说明 许丰提出了本文的研究思路和实验方案,并负责撰写论文、修订论文、审核论文;王所富负责碘盒体源模拟计算方法的前期理论研究工作;郭建友和於国兵负责统筹及调度气态碘采集实验的相关工作;徐平和王雪建负责摘要翻译,修订论文。
致谢 感谢安徽省辐射环境监督站顾先宝高级工程师,在方法的可行性讨论方面以及气态碘采集实验中给予的支持与帮助。

