基于粒子滤波算法的源项反演及不确定性分析
郑子豪 陈春花 朱婧娴 陈黎伟 王世鹏
1(中国科学院合肥物质科学研究院 合肥 230031)
2(中国科学技术大学 合肥 230026)
3(合肥师范学院计算机学院 合肥 230601)
“十四五”规划提出了以安全稳妥为前提,推动沿海核电项目建设,并提高核能综合利用的目标[1]。核能的发展以核安全为前提,核应急又是核安全最后一道屏障,源项分析是否精确决定了核应急行动的有效性。核事故发生后,源项信息通常难以直接获得,一般可利用厂外监测数据以及核素扩散模型推演得到源项信息,此过程为源项反演[2]。
近些年许多新的算法应用于源项反演,例如布谷鸟搜索算法、计算流体力学算法、粒子群优化算法和截断总体最小二乘变分法。Wang等[3]利用改进的布谷鸟搜索算法预测未知释放源的数量和坐标,结果表明,噪声信噪比越大、监测范围越广时,对释放源的追踪结果越精确;Kovalets等[4]利用计算流体力学对未知泄漏源的位置进行了反演,相比结合了贝叶斯理论或卡尔曼滤波的大气弥散模型,其结果的误差减少了一个数量级;黎岢等[5]利用粒子群优化算法对气态137Cs 进行了反演,并且设置了286个观测点,在释放率稳定的情况下,可以很好地追踪到真值,非稳态情况估计结果较差;刘蕴等[6]通过建立截断总体二乘变分核事故源项反演数值计算模型,在释放率稳定的条件下,结果相对真值有20%的误差。以上方法对背景条件设置较为理想,普遍侧重研究稳态的源项释放,对监测器数量和模拟数据设置过多,对噪音设定单一且不变。为了让反演过程更加符合现实,还应针对变化的监测噪音、有限的监测数据和非稳态的源项释放率进行研究。
考虑到监测噪音复杂多变,引入粒子滤波来降低噪音。由于粒子滤波算法需要将源项释放状态和源项扩散状态作为输入,本文在仅有两组监测数据的条件下,结合大气扩散模型,一组数据用于研究核事故初期源项瞬时释放率的递归关系,将其作为粒子滤波的状态方程;另一组数据作为测量数据,用作粒子滤波的测量方程。以此建立了在核事故发生初期,源项瞬时释放率多变、监测器有限和多重噪音干扰条件下的基于粒子滤波的源项反演方法。最后对整个反演过程进行不确定性分析,并证实可以此方法可以得到较为精确的反演结果。
1 原理与方法
本文根据源项的不同释放状态和放射性核素在大气中的扩散规律,建立了基于粒子滤波的实时反演方法。同时针对事故源项的特点,建立瞬时释放率状态方程,且对监测噪音变化规律进行了模拟假设。
1.1 源项状态模型
核事故发生后,源项瞬时释放量的状态方程[7]为(1)式,测量方程为(2)式。

式中:Yk为监测向量;Hk(Q1,Q2,...,Qk)为观测函数,代表烟团释放至大气后的扩散的规律;rk在本文中是监测仪器的测量相对误差和其他干扰项的统一表达。
1.2 粒子滤波算法
粒子滤波基于蒙特卡罗模拟方法实现递推贝叶斯滤波估计,对于系统的过程噪声和量测噪声没有的限制[8]。粒子滤波实时追踪源项的步骤如下四个步骤。
步骤一:设定初始值,分配初始权重。人为地设定一个初始值Q1代表释放量的初始数据,采集n个粒子样本,每个粒子叠加噪音q1,见(3)式。

用式(7)可以得到t= 2 时刻Q2的最小均方估计。


下一个时刻t=k+ 1,转到步骤三中对粒子重采样,再到步骤四中更新权值,并以此迭代。
1.3 大气扩散模型
余琦等[9]模拟了稳定流场和非稳定流场中烟羽模型和烟团模型扩散变化,其结果表明,烟团模型的精度更高,同时对于连续性释放,单位时间内释放的烟团越多,精度越高。为了研究核事故初期源项瞬时释放量,本文选择高斯烟团模型,并设定每秒钟释放一个烟团,故每个烟团所含的放射总活度为源项的瞬时释放率。假设泄漏源的坐标为原点,分别以正东和正北方向为X轴和Y轴,垂直于地面向上为Z轴,建立空间直角坐标系。开始泄漏时间T=0,当T=t秒时第i=t个烟团开始释放,源项此时瞬时释放率为Qt,此烟团经过τ秒后,用式(12)计算得到(x,y,z)处的活度浓度。
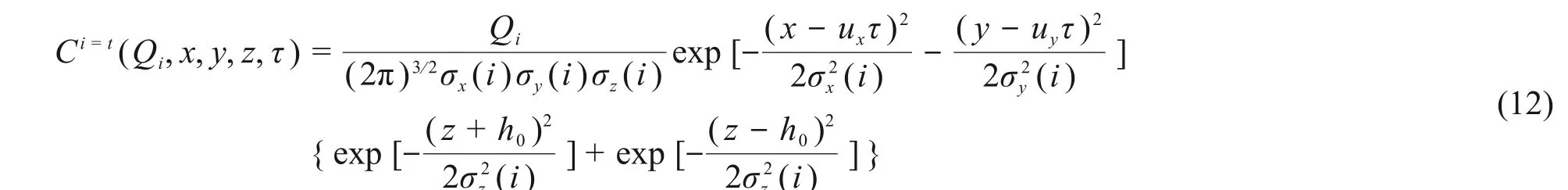
式中:Qi为需要反演的数据,Bq/s;σx(i)、σy(i)和σz(i)为大气扩散参数,表示第i=t个烟团在水平和垂直方向的扩散参数,其数值可参考Briggs修正公式[10];ux和uy为风速在X轴和Y轴上的分量,m/s;h0为烟团的有效释放高度,m。为了使扩散更好地模拟各种气象条件下的扩散过程,本文还考虑了烟团扩散时的干沉降、放射性核素的种类及其衰变修正[11]。
由于释放率Qi与其他客观条件相互独立,可将其与时间τ进行变量分离,将点(x,y,z)处关于时间τ的函数设为Singlepuff(τ)。Singlepuff(τ)为高斯函数,反映了烟团扩散的规律,将式(12)简化表示为式(13)。
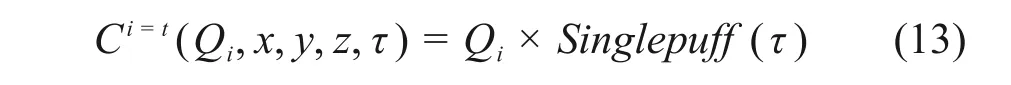
当泄漏时间为T=t时,所有已释放的烟团在(x,y,z)的活度浓度累计贡献为式(14)。

1.4 瞬时释放率状态方程的构建
Singlepuff(τ)与源项的释放率无关,在时间上呈现高斯分布,其特点是在某一时间内有着最大值,随着此时间增大或减少,其数值下降快且趋近于0,且函数在时间上的积分快速收敛。根据公式(2)和(14),将观测函数Hk(Q1,Q2,...,Qk)改写成矩阵形式,见式(15)。
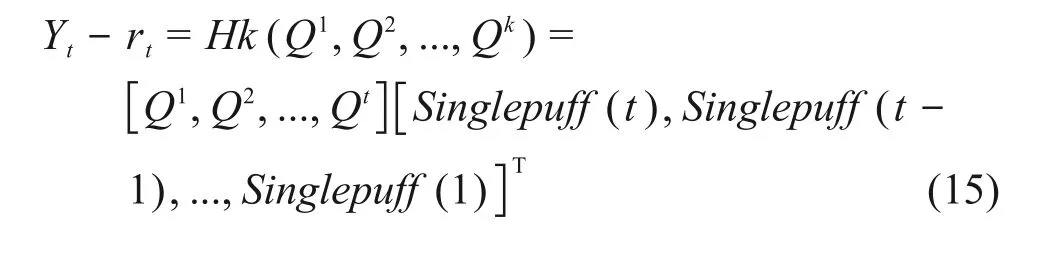
式中:rt为监测噪音。由式(15)可以得到,状态矩阵[Q1,Q2,...,Qt]与Singlepuff(t)之间随着时间呈现着有序的对应关系。因此可以通过监测数据Yt变化的趋势判断源项瞬时释放率变化状态,由此建立状态方程。
(1)当源项释放率连续恒定,可以认为每秒释放的烟团总活度相等,由于设函数Singlepuff(t)在时间的积分等于HK,根据式(15)有式(16)。
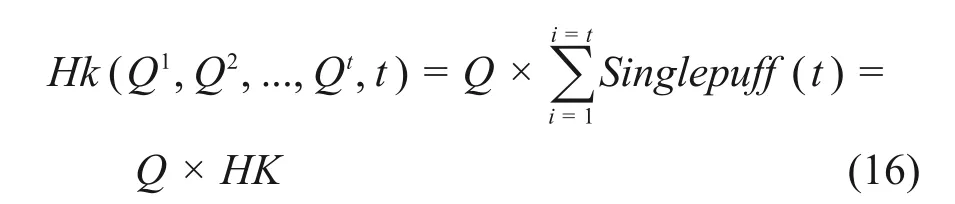
式中:Q和HK均为固定值,当监测数据长时间在某个数值稳定波动时,可以认定此时释放率稳定不变,此时状态方程见式(17)。

(2)当泄漏源的瞬时释放率为线性变化时,设每秒钟释放率变化k,由式(15)有方程组(18)。将式(18)两式相减可得(19)式。
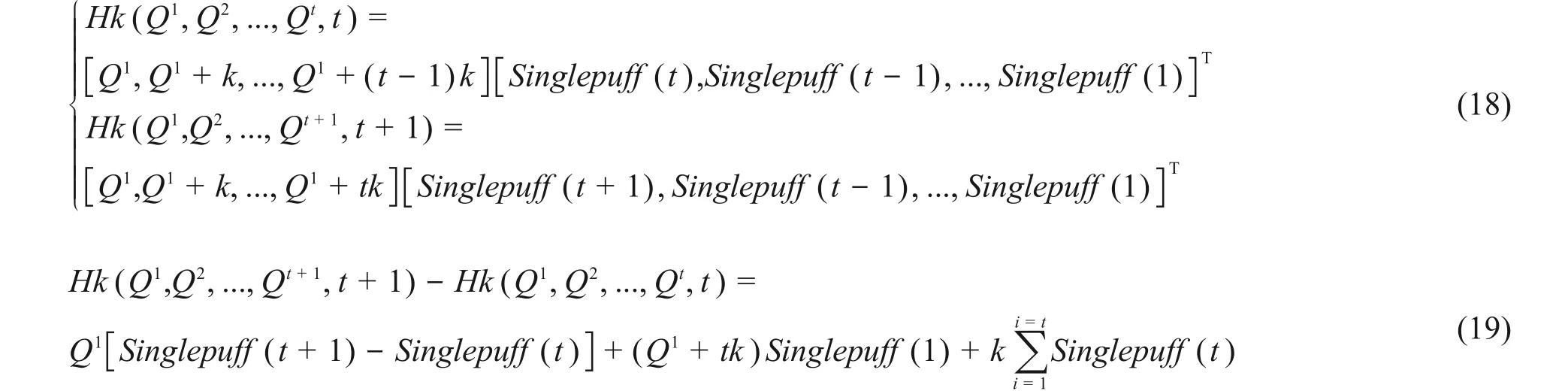
当t大于ux/x和uy/y时,第一个烟团开始往远离监测点的方向扩散,第t+1时刻的烟团还没有开始随风扩散,公式(19)前两项约等于0,得(20)式。



可以得到在tx时的平均释放率为公式(23)。
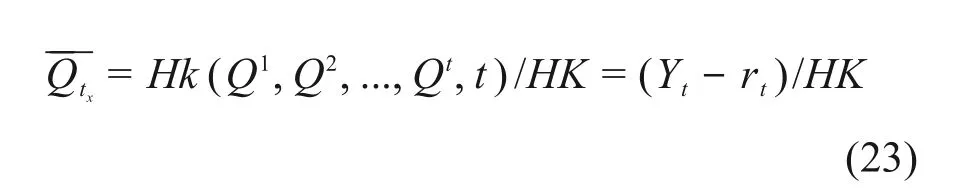
此方法计算出的释放率具有tx的偏移,具体的偏移范围与气象状况和监测器相对地理位置有关。将平均释放率--Qx代入高斯烟团模型正演其扩散规律,并与实际的监测数据比较后得到偏移量tx。
图1(a)是核事故发生后600 s 内的监测数据;图1(b)是计算出的平均释放率,可见,其变化的趋势与监测数据相同;图1(c)是平均释放率正演的结果与监测数据的对比,由于使用平均释放率作为瞬时释放率,正演数据相比监测数据平滑,根据图像可以判断偏移时间tx;图1(d)表示时间修正后的释放率。这样求得的平均释放率因监测误差而在真值附近波动,对释放率进行拟合,用拟合后的曲线作为状态方程。
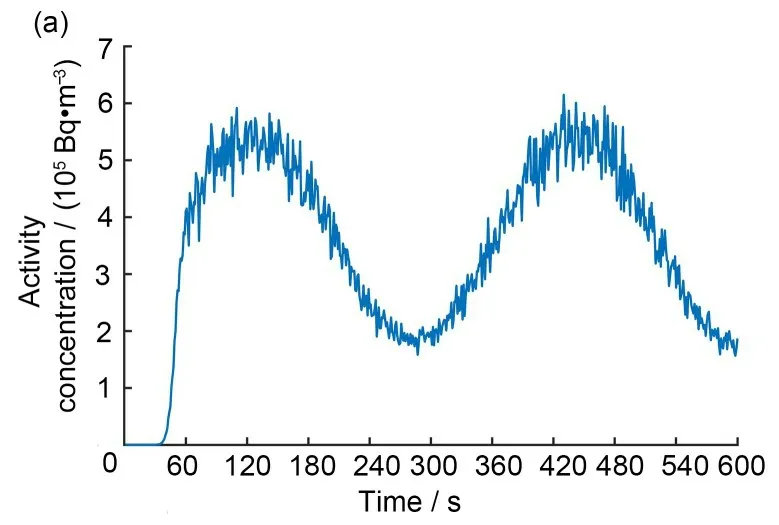

图1 释放率连续变化时的状态方程建立流程:(a)核事故发生后600 s内的监测数据;(b)计算得到的平均释放率;(c)平均释放率正演的结果与监测数据的对比;(d)时间修正后的释放率与拟合曲线Fig.1 The process of establishing the equation of state when the release rate changes continuously:(a)monitoring data within 600 s after the nuclear accident;(b)calculated average release rate;(c)comparison between the forward modeling results of average release rate and monitoring data;(d)time corrected release rate and fitting curve
1.5 监测噪音
一般认为,监测器的实时监测数据包含着此刻源项由大气扩散后在周围空气中的活度浓度,并叠加监测器的观测误差。Morino等[12]模拟了福岛核事故中131I 和137Cs 因干湿沉积累计到地面上的活度,其分别占释放总活度的8.2%和11.7%。Hu[13]模拟计算了不同的源项释放率的沉积过程,其结果表明,不同的释放率、天气、风向等因素,对放射性核素沉积到地面所污染的面积、污染的分布及其最大沉积活度均有影响。因此,具体某时刻的监测数据还应该包含核事故发生后、此时刻之前放射性核素的历史沉积。由于本文源项瞬时释放率是未知的,根据文献[13]的结果可以对历史沉积的总活度进行定性分析:在同一时刻,距离下风向和侧风向越远,其沉降的总活度越低。针对放射性物质沉积对监测数据的影响,在源项反演模拟过程中,设置为随着时间逐渐增大的均匀噪声,与监测器固有误差进行叠加后,即为公式(2)中的rk。
2 仿真实验和不确定性分析
2.1 仿真实验设定
实验模拟在核事故发生后t时刻,131I以3种不同的释放状态持续泄漏至环境中,瞬时释放率分别为:稳定状态,Q= 1 × 1010Bq/s;线性增长状态,Q(t) = 108+t× 109Bq/s;正弦变化状态,Q(t) = 109×(2 + sin(t/100)) Bq/s。131I 的 半 衰 期设置为8.07 d,仅布置两个监测位点。
实验的气象条件设定:大气稳定度为C类;风速为2 m/s;风向为东风;无降雨。地理信息设定:以泄漏源为坐标原点、正东方向为X轴、正北方向为Y轴、垂直于地面为Z轴建立空间直角坐标系,监测器A坐标为(50,20,10),监测器B的坐标为(100,20,10);烟团有效释放高度为10 m。反演时间设定:核事故发生后t=1 s 开始,监测器每秒钟传回监测数据,泄漏时间360 s 后开始反演。监测噪声设定:两个监测器相对测量误差均为20%,监测器A 在t=60 s 后每隔60 s 叠加0~2%的均匀噪声,监测器B 在t=120 s 后每隔60 s 叠加0~0.5%的均匀噪声。粒子滤波的粒子数设置为100。
考虑到监测器B距离泄漏点更远,其受到的噪音干扰相对更小,因此实验中利用监测器B的监测数据设定状态方程,过程误差协方差矩阵用过程噪声相对误差10%计算,利用监测器A 的监测数据作为粒子滤波的观测值。
2.2 计算状态方程
根据§1.4瞬时释放率状态方程构建的方法。
(1)当释放率连续稳定时,测量得到的释放率如图2(a)所示,设定释放状态方程为Q= 1.05 ×1010Bq/s。(2)当释放率线性增长时,其测量释放率如图2(b)所示,t=1 s 时释放率的计算测量值为Q(1) = 1.8 × 109Bq/s,将其设为释放状态方程的初始值,根据图像状态方程设定为Q(t) =Q(t−1) + 1.02 × 109Bq/s。(3)当释放率正弦变化时,其测量释放率如图2(c)所示,经过时间修正后得到前300 s的平均释放率如图2(d)所示。对曲线进行拟合,选择图2(d)中最高处的点,并以此点为中心选择另外两个相对称的点,计算经过这3个点的二次函数,并以此作拟合曲线,有Q(t)=−3.89×104×t2+1.26×107×t+2×109Bq/s,用此函数作为状态方程。
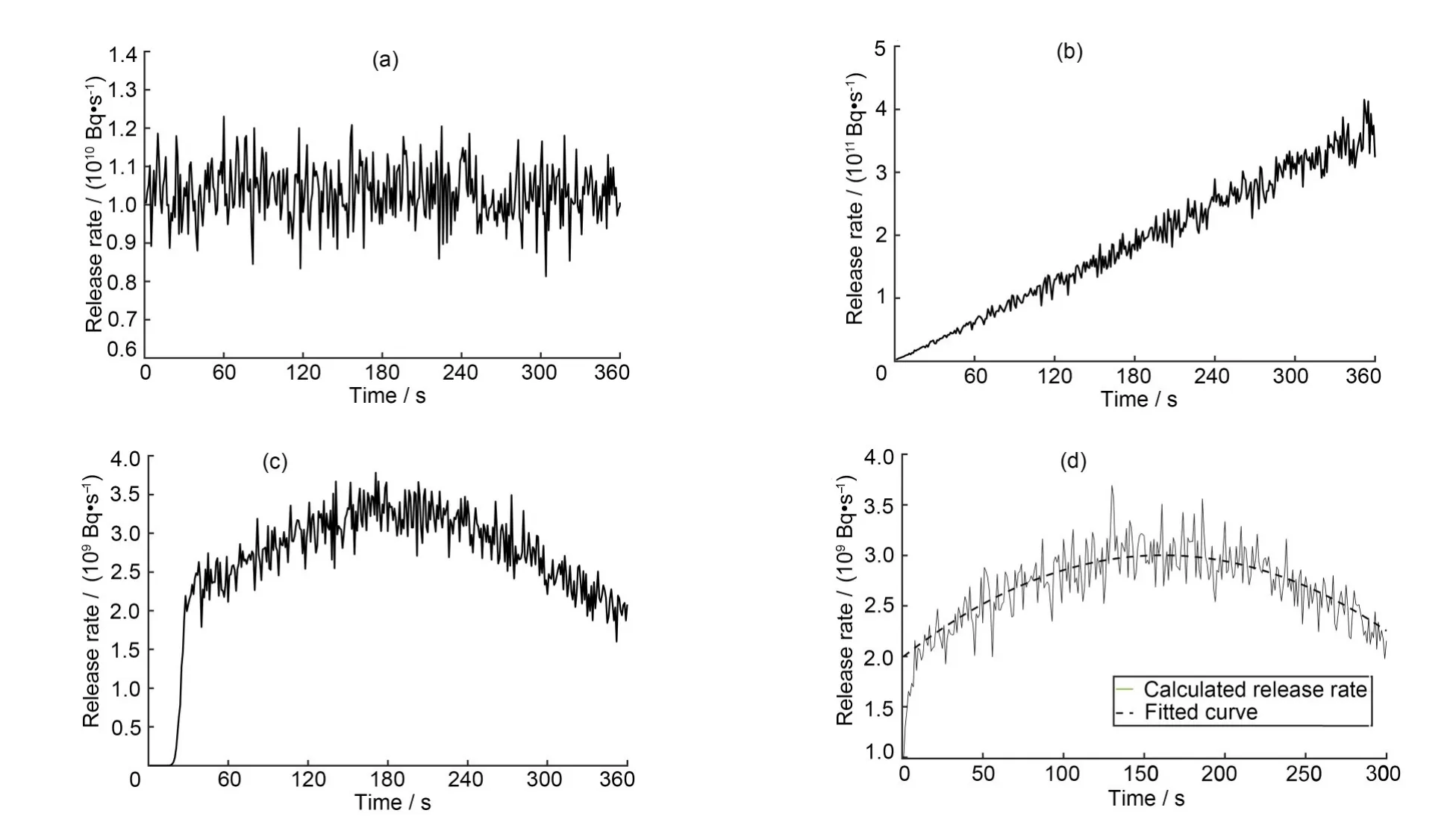
图2 由监测数据计算而得的释放率:(a)释放率稳定不变时的计算值;(b)释放率线性变化时的计算值;(c)释放率正弦变化时的计算值;(d)释放率正弦变化时的修正数据和拟合曲线Fig.2 Calculated release rate from the monitoring data:(a)calculated value when the release rate is stable;(b)calculated value when the release rate changes linearly;(c)calculated value when the release rate changes sinusoidally;(d)correction data and fitting curve of sinusoidal change of release rate
2.3 实验结果
三种释放状态的测量值和滤波值以及它们相对于真值的误差如图3 所示,根据图3(a)、(c)和(e),滤波值相对测量值波动范围减小,整体更加平滑;根据图3(b)、(d)和(f)的误差曲线,滤波值最终在真值附近波动,相对真值的误差约5%,最大不超过10%。当释放率为线性增长时,由于状态方程设定初始值相比真值较大,前60 s滤波值误差呈现逐渐减小的趋势,在60 s后误差在3%波动。由于监测器的相对误差设定在20%,说明粒子滤波可以有效地减少误差,反演结果优于计算测量值。
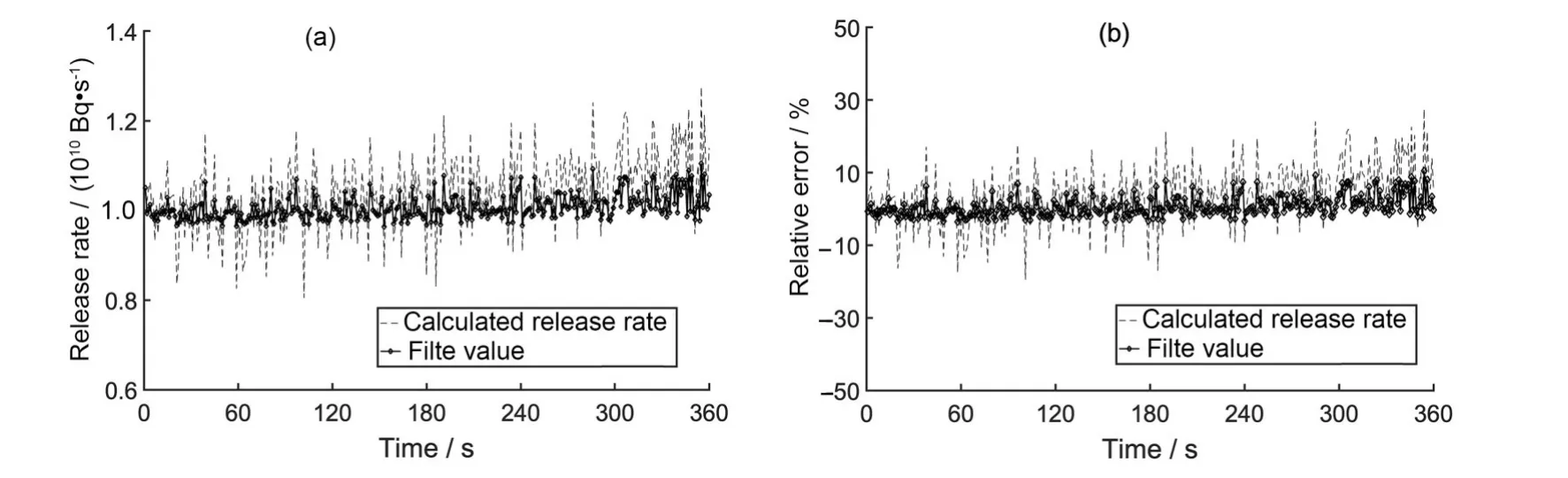
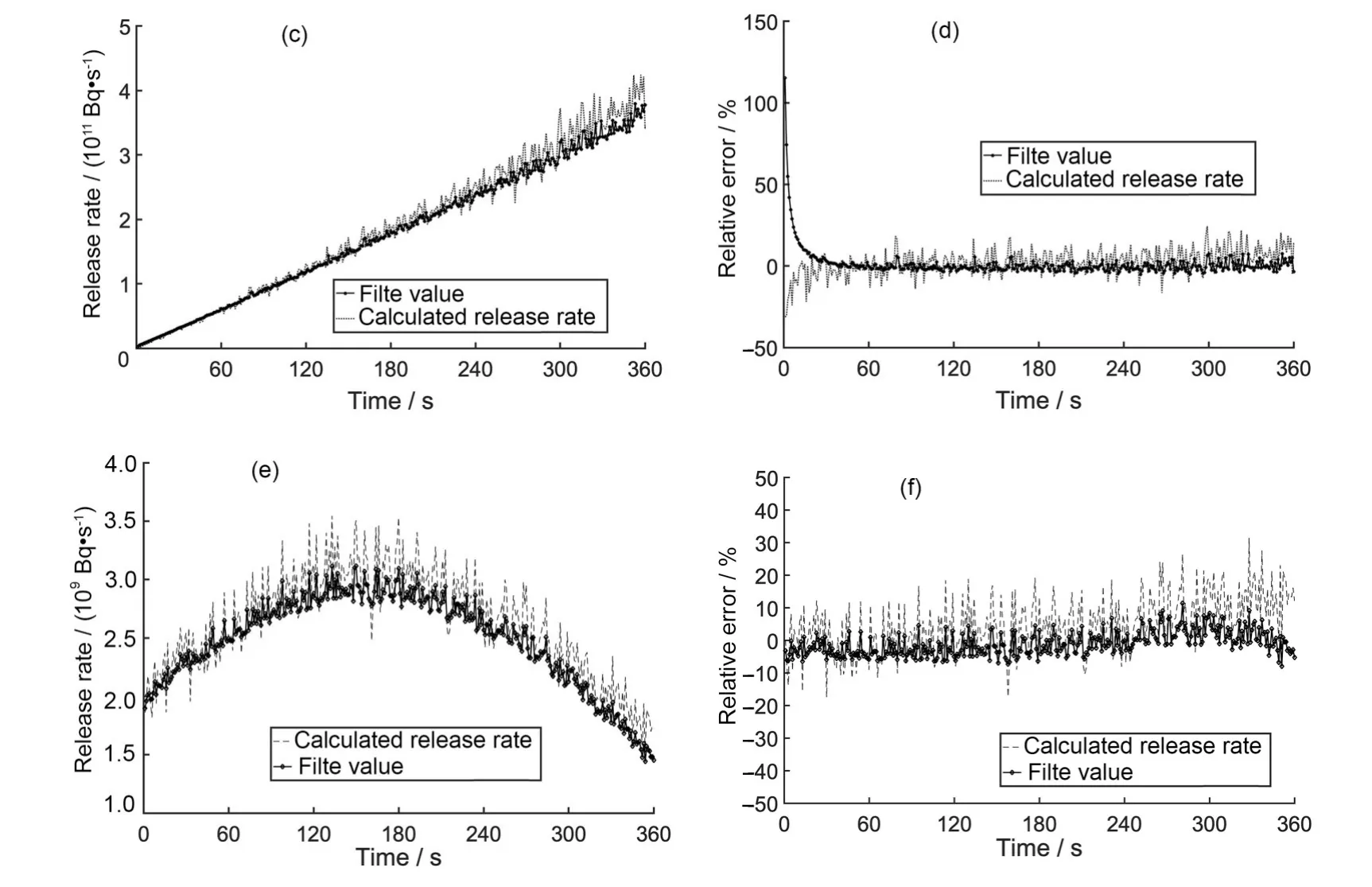
图3 稳定(a)、(b),线性变化(c)、(d),和正弦变化(e)、(f)的源项释放粒子滤波反演结果Fig.3 Particle filter inversion results of stable release(a),(b),linear release(c),(d),and sine release(e),(f)
2.4 粒子数和过程噪声相对误差对滤波结果的影响
粒子滤波算法的粒子数量代表着每次随机采样的次数,当采样的范围已被确定时,采样次数越多,粒子落在真值处的概率越大。还需讨论在特定的过程噪声相对误差下,粒子数设定对滤波结果的影响。
当释放率线性增长、过程噪声相对误差为10%时,分别设置粒子数为50、100、1 000。粒子滤波反演如图4所示,不同的粒子数有着几乎相同的结果。由于较小的过程噪声将粒子每次采样限定在很小的范围内,当过程噪声相对误差不大于监测器相对测量误差时,粒子数不是减少反演误差的主要因素。

图4 过程噪声相对误差为10%时粒子数为50、100、1000的粒子滤波反演结果Fig.4 Particle filter inversion results with particle numbers of 50,100 and 1 000 when the process noise covariance matrix is 10%
设置过程噪声相对误差为50%,此时过程噪声大于监测器噪声,粒子滤波器相信监测数据,此时粒子滤波的作用不再是过滤噪声,而是追踪测量值。分别设置粒子数为50、100、1 000,粒子滤波反演结果的误差如图5 所示,当粒子数为1 000 时,反演值与测量值拟合结果优秀,几乎没有波动。以粒子数为1 000 时为基准,如图5(a)所示,当粒子数为50 时,反演结果与测量值的拟合较差;当粒子数为100时,反演结果在测量值附近波动,波动范围不小于20%。
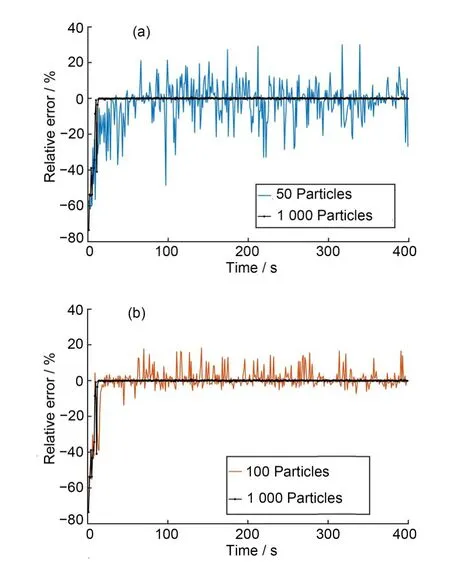
图5 以1 000为基准,粒子数分别为50(a)和100(b)时的结果相对误差Fig.5 Based on 1 000,the relative error of the results when the number of particles is 50(a)and 100(b)
根据实验结果可以看出,当状态方程比监测值精确时,粒子数对反演结果影响较小;当状态方程误差比监测值更大时,滤波结果偏向于与监测值拟合,粒子数设置越多拟合程度越好。综合两种情况考虑,粒子数设置偏向于越多越好,但增加粒子数量会导致计算时间增长,因此粒子数设置需要同时兼顾状态方程误差和计算机性能。由于本文实验设定状态方程的数据来源于受到噪音干扰较小的监测器,故设置100个粒子时,即可获得较佳的结果。
2.5 初始值对滤波结果的影响
粒子滤波算法中,状态方程的初值是人为设定的。为了探讨人为设定的初始值对滤波结果的影响,分别以源项初始释放率真值的0.1%、1%、10%、100%、1 000%和10 000%作为粒子滤波的初始值,当源项释放率线性增加时,设置Q(t) =108+t× 109Bq/s,反演结果相对真值的误差,如图6(a)所示,当初始值设定小于100%初值真值时,粒子滤波反演值可以快速追踪到真值;当初始值设定大于100%真值时,粒子滤波反演值趋向于真值,随着初始值增大,粒子滤波接近真值的速度越来越慢。
当释放率线性减少时,设置Q(t) = 1011−t× 109Bq/s,分别设定源项初始释放率真值的0.1%、1%、10%、100%、1 000%和10 000%作为粒子滤波的初始值。反演结果误差的对数如图6(b)所示,当设定的初始值远小于或者远大于真值时,结果的误差极大;当初始值在真值附近时,相对误差的对数在±1之间,即±10%。
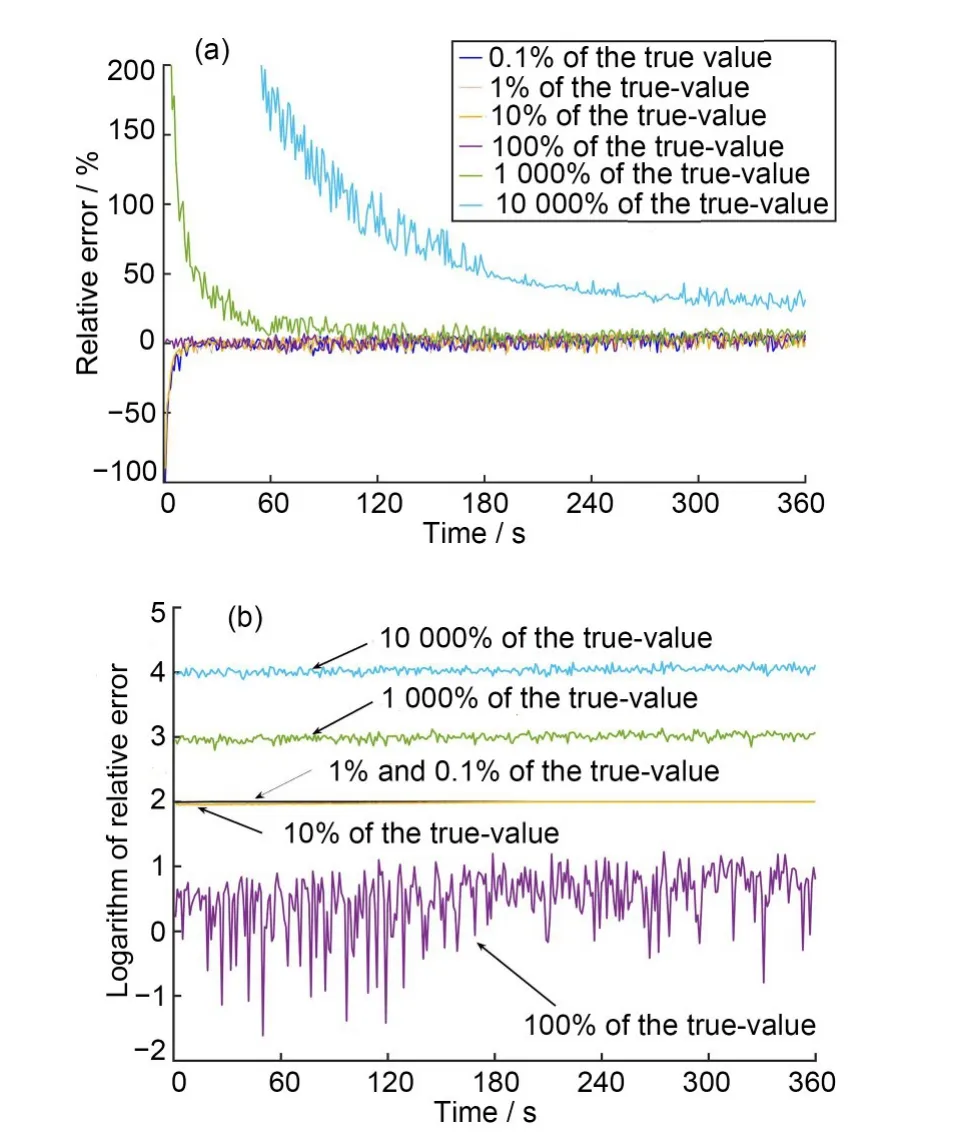
图6 线性增加(a)和线性减少(b)时不同初值对粒子滤波反演的影响(彩色见网络版)Fig.6 Influence of different initial values with linear increase(a)and linear decrease(b)on particle filter inversion(color online)
根据以上分析可以得出结论,在粒子滤波反演源项中,初始值的设定不存在偏大或者偏小的偏好规律,为了得到最优的反演结果,应该始终以实际的监测数据作为参考。
2.6 监测器误差对粒子滤波的影响
现实中不同的监测仪器、不同的环境、不同的使用方式等因素,均可导致不同的测量误差[14]。为了探讨监测器的相对测量误差对滤波结果的影响,分别以5%、20%和50%为例,当释放率恒定时,分别计算这三种不同的误差所对应的滤波结果。
当相对监测误差为5%时,测量释放率与粒子滤波反演结果如图7 所示。滤波值与测量值几乎重合,由于预测初始值相对真值误差比监测值大,前60 s的反演值相比测量值稍大,在180 s后由于均匀噪声越来越大,反演值开始小于测量值,并且相比测量值更加接近于真值。由结果可知,当监测器相对测量误差小于状态方程的过程噪声相对误差时,滤波器相信监测数据,反演结果与测量释放率大致相同。

图7 监测相对误差为5%时粒子滤波反演结果Fig.7 Particle filter inversion results when the observation noise covariance matrix is 5%
当相对监测误差为20%时,根据图3(a)和(b),粒子滤波反演值相比测量值更加平滑,精确度更高;当相对监测误差为50%时,反演结果和测量值相对于真值的误差如图8所示,与图3(b)的结果类似,粒子滤波的误差波动相比测量值更小,更加靠近真值。由结果可知,当监测器相对测量误差大于状态方程的过程噪声相对误差时,粒子滤波器相信状态方程,反演结果不被增大的相对监测误差影响。
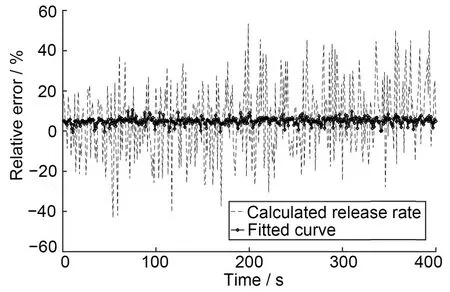
图8 监测误差为50%时的粒子滤波反演误差与测量误差Fig.8 Particle filter inversion error and measurement error when the noise covariance matrix is 50%
2.7 讨论
考虑到现实中监测器布置有限,实验只设定了两组监测数据,分别用于建立状态方程和作为粒子滤波的数据输入,粒子滤波反演的结果相对真值误差更小、数据波动幅度更低,说明粒子滤波在此反演模型中可以很好的过滤噪声。
状态方程的准确性是粒子滤波能有效地过滤噪声的前提。当设定的状态方程的误差过大时,可以设置较大的过程噪声,并设置大量的粒子数,滤波值才可以很好地与监测数据拟合;当设定状态方程误差过大,但设置较小的过程噪声时,滤波值结果无法与监测数据拟合。实验中状态方程建立源自于监测数据,状态方程近似于对监测结果的拟合,因此其相对误差与监测数据的相对误差近似。根据粒子滤波原理,当状态方程和观测方程的相对误差较为接近时,滤波后的结果才可以很明显地降低噪音。综合以上实验结果和不确定性分析可以得知,如果有其他的途径获得误差更小的状态方程,源项反演的滤波结果将越为准确,可见实施对源项变化趋势的研究也应该是源项反演的重要工作。
3 结论
本文研究了在源项释放率连续多变、监测器数量有限以及监测噪音多变的情况下,基于粒子滤波的源项反演方法。结果表明,仅使用两组监测数据,选择受噪音干扰较小的监测数据设定源项释放率的状态方程和初值;选择受噪音干扰较大的监测数据设定为粒子滤波观测数据;设置粒子滤波的粒子数100,当监测器均误差为20%时,反演结果相对真值的误差在±5%附近波动,最大不超过10%。此方法针对多种释放场景有着类似的结果,原则上可以用于核事故发生早期对源项瞬时释放率的反演计算。
作者贡献说明 郑子豪论文初稿撰写,论文审阅与修订,实验仿真模拟和实验结果分析;陈春花研究内容总体设计;朱婧娴实际调查研究与项目管理;陈黎伟模型测试;王世鹏研究方法指导。全体作者均已阅读并同意最终的文本。

