基于变区间阈值法的河道生态需水计算方法

何奇锴，熊 莹，吴贞晖，姚华明，4，5，王现勋

（1.油气地球化学与环境湖北省重点实验室（长江大学资源与环境学院），武汉 430100；2.长江水利委员会水文局，武汉 430010；3.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；4.中国长江电力股份有限公司，湖北宜昌 443000；5.智慧长江与水电科学湖北省重点实验室，湖北宜昌 443000）

0 引 言

水库通过调节径流达到防洪、发电和灌溉等兴利目的同时，也在一定程度上改变了河道的生态情势，对下游河道生态系统造成一定的胁迫［1］。因此需要通过水库生态调度权衡人类与下游生态系统之间的相互关系，开展满足下游生态需水量的水库调度方式。河流生态需水量的确定是制定生态调度方案的前提和依据，也是生态学、水文学和水资源学等领域的研究热点［2］。

现阶段国内外学者已对生态需水计算方法进行了广泛的研究，并取得一定的成果。目前其计算方法可分为水文学法、水力学法、栖息地模拟法以及整体法［3］。常用的水文学法有Tennant 法、7Q10 法［4］和IHA-RVA 法（Indicators of Hydrologic Alteration-Range of Variability Approach）［5］，DFM 法等。Tennant 于1976年提出的Tennant 法最具代表性，用以评估河流健康的最低生态流量标准，奠定了河道生态需水量的理论基础［6］。Tan 等［7］提出了一种基于变带宽核密度估计法的生态需水量计算方法分布流量法（Distribution Flow Method，DFM），该方法考虑了自然径流在年内和年际变化，从而减少了年内极端流量和不均匀流量分布的影响。这类方法简单、资料易获取但忽略了河流流量季节性变化。常见的水力学法有河道湿周法［8］和R2Cross 法［9］等，这类方法包含了更为具体的河流信息［10］，却忽视了河流中具体的物种或生命阶段的需求，计算时间较长且资料的获取较耗费人力和物力。栖息地模拟法常用的有河道内流量增加法（IFIM）［11］和加权有效宽度（WUW）法等，考虑了年际中多物种及其不同生命阶段所利用栖息地的变化［12］。整体法包括BBM 法（Building Block Methodology）［13］和专家组评价法等，这类方法是建立在尽量维持河流水生态系统原始功能的原则之上，然而生态资料等信息的缺乏往往给栖息地法和整体法的应用带来了困难。水文学法因为所需数据资料少，容易获得，且计算简便，在生态需水计算领域得到了广泛的应用［14］。以Tennant 法为代表的基流法，只关注生态需水下限，便于转化为河流评价指标（如生态需水保证率），但未考虑上限而存在一定不足，例如特大洪水并非生态所需。另一类方法为以分布流量法（DFM）为代表的区间法，该类方法将生态需水设定为有上、下限的区间阈值，更贴近于实际要求。有待商榷的是，是否有必要将全年所有时段的生态需水都设置为区间阈值。

针对目前生态需水研究的不足，本文尝试构造一种考虑年内径流变化程度的生态需水计算组合方法——变区间阈值法，即根据年内各时段径流方差的差异，选用基流法或区间法确定生态需水；并通过构建多目标调度模型和案例分析，对比验证所提方法的可行性和有效性。

1 方 法

1.1 变区间阈值法

本方法根据径流年内丰枯变化的差异，划分枯水期和丰水期，分别对不同月份计算生态需水。鉴于枯水期径流方差小，将较低生态流量作为生态需水下限处理，即取Tennant 法计算的生态流量和已知年均流量的最小值较小者作为该时期下阈值；丰水期径流方差较大，生态需水设置为一个区间，采用分布流量法计算得到的生态流量作为其生态需水上、下阈值。逐旬径流方差计算结果见表1。

表1 逐旬径流方差Tab.1 Ten-day runoff variance

由此，根据年内各月径流方差的差异，将基流法和区间法的优势特征相结合，构造一种能够考虑年内径流变化程度的生态需水组合方法。该方法的计算步骤如下：

（1）在枯水期，结合Tennant 法确定的生态流量Q1，i和多年平均流量最小值Q2，min，计算各旬的河道基本生态需水量Qi，即：

（2）在丰水期，用分布流量法计算生态需水上、下阈值，上（下）阈值以逐旬流量最大（小）值组成的多年旬平均流量为输入序列，适宜生态需水以逐旬流量均值组成的多年旬平均流量为输入序列，采用基于变带宽核密度估计法的分布流量法确定其阈值，且核密度估计的好坏取决于核函数和带宽h［15］，其中带宽h的最优选择（使平均积分平方误差最小化的带宽）为式（3），核函数为式（4）：

式中：{x1，…，xn}为离散的随机样本为总体未知密度函数f(x)一个核估计；n为样本容量是样品的标准差。

1.2 多目标调度模型

为验证本文所提生态需水新方法的有效性和合理性，下文构建水库生态调度多目标优化模型，以某水库为对象开展实例研究，分别使用本文所提方法、Tennant 法和分布流量法确定生态需水，进而对比分析水库生态调度运行结果差异。

本文所建调度模型以发电量最大和生态缺溢水量［16］最小为优化目标，通过权重法将多目标优化问题转化成单目标优化问题［17］。

模型目标函数的数学表达式为：

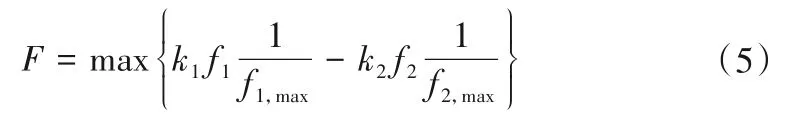
式中：F 表示各目标赋予权重后线性叠加的总目标；ki表示第i个子目标的权重，且= 1；fi表示第i 个子目标的值；fi，max为子目标单目标优化的时段最大值，以此统一各子目标加权计算时的量纲；N=2，表示子目标的个数。各子目标的具体计算公式如下：

（1）发电目标：

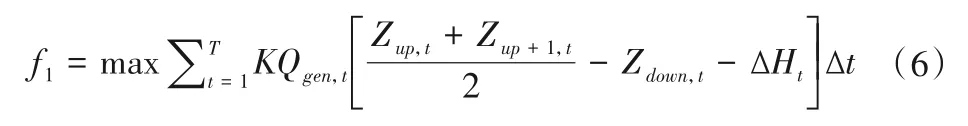
式中：f1为目标发电量最大，kWh；T 为计算时段总数；Δt 为单位时段的时长，旬；K为水电站综合出力系数；Qgen，t为电站第t时段的发电引用流量，m³/s；Zup，t、Zup+1，t分别为电站在第t 时段和第t + 1时段初的上游库水位，m；Zdown，t为电站第t时段的下游尾水位，m；ΔHt为电站第t时段的水头损失，m。

（2）生态目标：

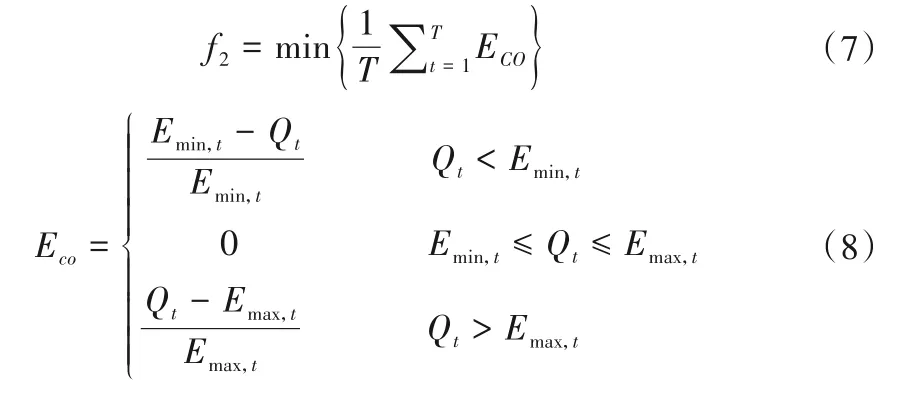
式中：f2为目标生态溢缺水量最小；T 为计算时段总数；ECO为出库流量与生态需水之间的归一化距离；Emin，t和Emax，t分别为t 时段生态需水下阈值和上阈值；Qt为t时段的出库流量，m3/s。

1.3 约束条件

（1）水量平衡约束：

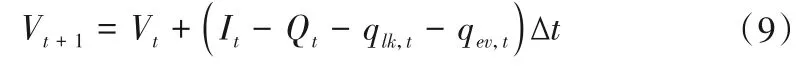
式中：Vt+1为t时段末水库的库容，m³；Vt为t时段初水库的库容，m³；It为t 时段的入库流量，m³/s；Qt为t 时段的出库流量，m³/s；qlk，t为t 时段的渗漏损失流量，m³/s；qev，t为t 时段的蒸发损失流量，m³/s。

（2）流量约束：

式中：Qt，min为t 时段允许的最小下泄流量（如最小生态流量、供水流量等），m³/s；Qt，max为t 时段允许的最大下泄流量（如泄流能力，安全泄量等），m³/s。

（3）时段水位约束：

式中：Zt为t时段水库的水位，m；Zt，min、Zt，max分别为t时段最低限制水位和最高限制水位。

（4）出力约束：

式中：Nt，min为t 时段允许的最小出力，kW；Nt，max为t 时段允许的最大出力，kW。

（5）初末水位约束：

式中：Zbgn、Zend分别为计算期初、末水库水位，m。

1.4 模型求解方法

本文采用动态规划算法对模型进行求解，将水库时段初水位作为状态变量，时段末水位作为决策变量，发电和生态综合效益作为目标函数。具体求解步骤如下：

（1）划分阶段并确定状态变量和决策变量：首先假设年内按时段划分为t 个阶段变量，将水库水位Z 离散成n 个点（Z1为死水位，Zn为防洪限制水位），时段初水位Zi为状态变量，时段末水位Zj为决策变量，并确定水量、水位及出力等约束条件。

（2）构建状态转移方程：以决策变量和状态变量为计算变量，根据水量平衡和水位库容关系，列出系统各个阶段初、末状态间转换关系状态转移方程，以及代表全过程总效益的效益指标函数，结合各约束条件，筛选出满足条件的可行的决策变量与状态变量组合。

（3）按逆时序推求最优策略：根据最优化原理建立动态规划寻优递推计算的目标函数基本方程，计算出t+1 时段满足各约束条件的决策变量与状态变量对应的目标函数值，根据逆序递推方程，得出满足约束条件的最优策略。

1.5 研究对象及数据

三峡工程是当今世界综合效益最大的水利枢纽之一，自建库以来发挥着巨大的发电、防洪、航运等社会经济效益，同时对库区生态环境造成的生态问题也日益凸显［18］。因此本文选取三峡水库为研究对象，实例验证本文所提生态需水计算新方法的可行性。宜昌站是三峡水利枢纽工程的代表站［19］，故采用宜昌站1952-2012年宜昌站共61年逐月径流实测资料，以旬为计算时段。为了方便考虑年内径流分布情况，计算时确定6-9月为丰水期，10月-次年5月为枯水期。

2 结果与分析

2.1 方案选取及生态流量计算

本文设置了3 个方案计算生态流量：方案一采用变区间阈值法；方案二采用Tennant法；方案三采用分布流量法；

（1）方案一为本文提出的生态需水计算新方法：详见1.1 变区间阈值法。

（2）方案二利用Tennant 法计算水库生态需水。本研究中Tennant 法计算水库最小下泄流量的选取标准为“良好”，即4-9月取多年平均流量的40%作为推荐生态流量值，10月-次年3月多年平均流量的20%作为推荐生态流量值。

（3）方案三采用分布流量法（DFM）计算水库生态需水上下限，具体为：通过DFM 法计算得到逐旬最优生态需水上阈值和逐旬最优生态需水下阈值，选取旬下阈值和对应旬最小值较大的流量为该旬生态流量下限，旬上阈值和对应旬最大值较小的流量为该旬生态流量上限。

根据入库流量数据，分别对3个方案进行生态需水计算，得到水库各方案情况下生态流量过程，见图1。其中由Tennant法计算出“良好”标准下的河道基本生态需水过程，可以看出该过程在丰水期和枯水期分别为不同的固定流量值（枯水期：2 715.3 m3/s，丰水期：5 430.6 m3/s）。分布流量法计算出的生态流量过程在年内均为一个区间阈值。考虑到前两种方法在来水差异较大的丰水期和枯水期生态需水过程中可能产生的不足之处，本文研究的变区间阈值法在枯水期的生态流量值为定值，其值是Tennant 等在多条河流生态试验分析得到的，能代表水生栖息地适应性和流量之间的宏观关系［20］；在丰水期为区间阈值，考虑到河流年内季节的丰枯规律，更贴近实际。

图1 各方案适宜流量过程Fig.1 Suitable flow duration corresponding to each scheme

2.2 不同方案下非劣解分析

本文选取1952-2012年共61年宜昌站流量数据，采用动态规划算法对多目标调度模型进行求解，得到关于多年平均发电量和生态溢缺水量（ESD）的非劣解集，分析三种方案在不同权重情景下水库发电量与生态溢缺水量的关系。宜昌站各方案多年平均发电量-生态溢缺水量如表2所示，表中分别列出了发电目标和生态目标权重具体取值。

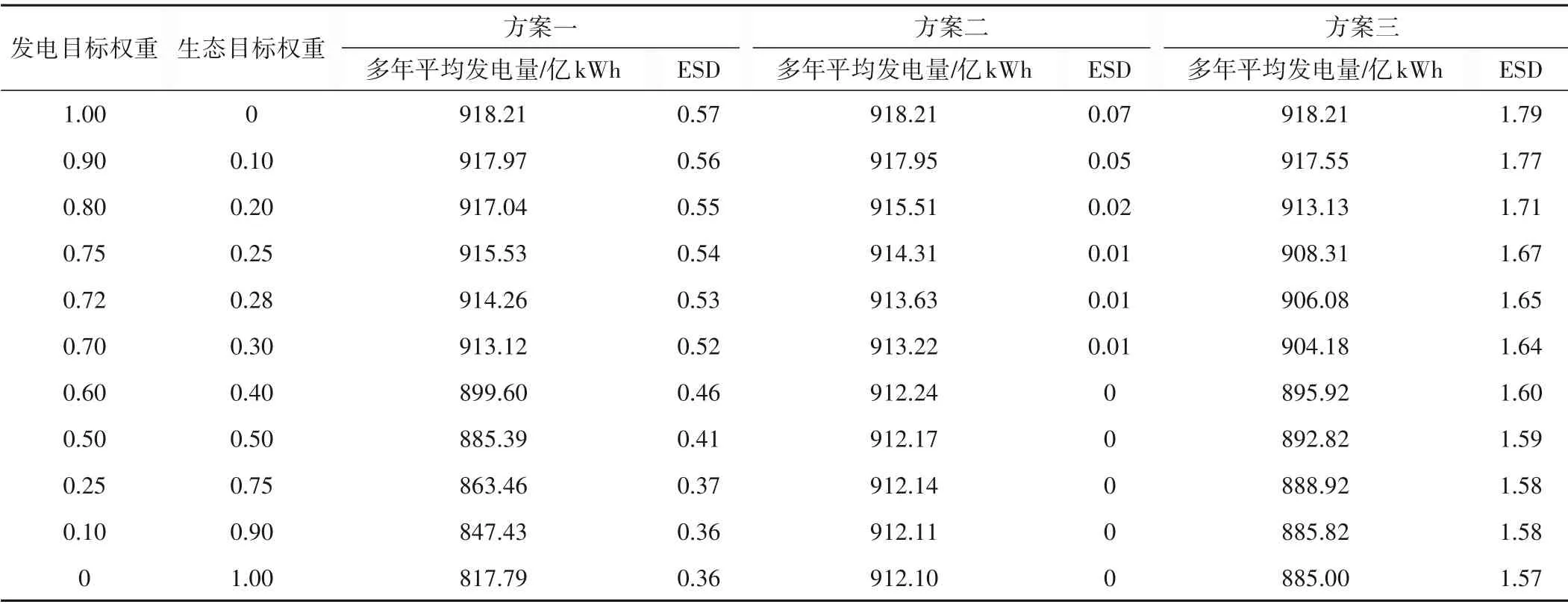
表2 多目标非劣解集Tab.2 Multi-objective pareto optimal solution sets

由表2可以看出，各方案中多年平均发电量越大，对应的生态溢缺水量指标值越小，而生态溢缺水量越低说明生态效益越好，表明发电效益的增加会在一定程度上导致生态效益的降低。下面通过分析不同方案下发电量和生态溢缺水量Pareto前沿，来验证本文研究的变区间阈值法的合理性。

由图2（a）可以看出，方案一下随着多年平均发电量逐渐增加，生态溢缺水量指标值逐渐增加，水库发电量与生态溢缺水量之间存在明显的正相关关系，Pareto 解集在发电量为900 亿kWh 以上时分布较为密集，在发电量为900 亿kWh 以下时分布较为均匀，由于本文对生态和发电的权重取值占比不同，当发电效益占比较大时，生态效益的占比就会降低，呈现出此消彼长的关系。发电效益增大到某一临界值后生态效益已然较低，继续增大发电效益对生态效益的影响程度逐渐降低，因此存在Pareto 最优解分布疏密不平等的情况。总体来看是一组具有代表性的非劣解。

由图2（b）可以看出，方案二下生态溢缺水量随着多年平均发电量的增加逐渐增加，虽然整体呈现正相关关系，但其Pareto最优解密集分布的区间较窄且分布不均，发电量在912.24 亿kWh 以下的非劣解对应的生态溢缺水量皆为0，在912.24 亿kWh 以上非劣解对应的生态溢缺水量与发电量呈现正相关增长，并且可以看出其生态溢缺水量指标值总体较小，从呈现的趋势上看该方案的非劣解集有着较好的生态效益。

由图2（c）可以看出，方案三下随着多年平均发电量逐渐增加，生态溢缺水量逐渐增加，同样呈现正相关关系，Pareto 最优解分布较为均匀但疏密不平等，Pareto 解集在900 亿kWh 以下时分布较密集，在900 亿kWh 以上时分布较均匀，该特点与方案一呈现趋势相反。

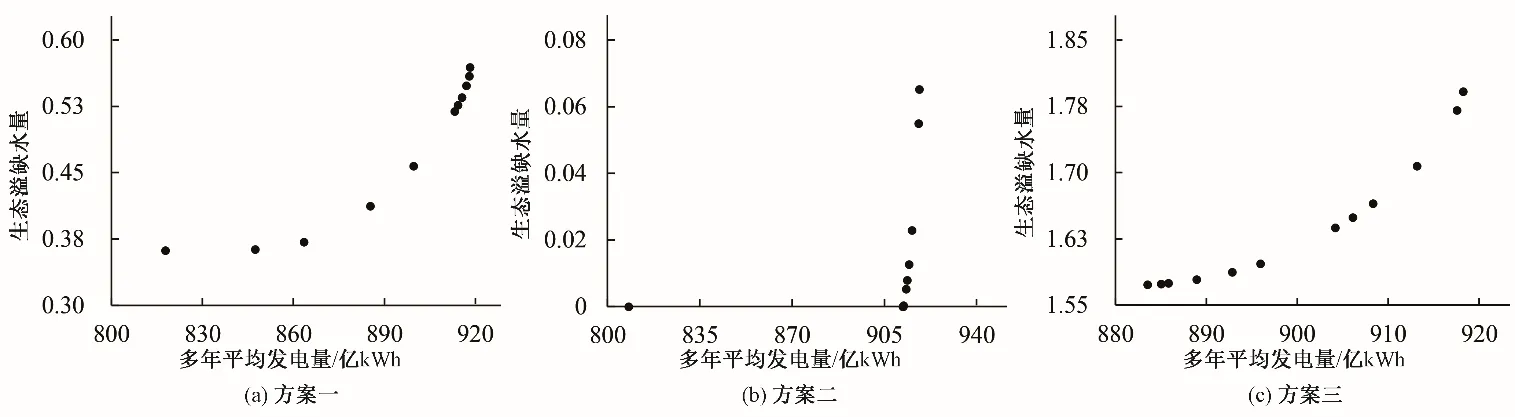
图2 不同方案Pareto最优解分布Fig.2 Pareto optimal solution distribution of different schemes

鉴于不同方案下计算的生态流量不同（定值或区间值），为准确地表示各方案的优劣程度，本文分别将3 个方案下计算得到的生态溢缺水量用统一的衡量标准来度量，以降低由于不同量纲所造成的误差［21］。具体处理算式见公式（14）。

式中：此时Qout，t，k为第k 种方案下第t 时段的出库流量；Emax，t为一较大常值，本文取为10 000 m3/s；Emin，t为Tennant 法计算得到的生态需水过程。

图3为变区间阈值法、分布流量法和Tennant法多年平均发电量与生态溢缺水量统一标度后的计算结果。由图3 可以看出，在相同发电量的条件下，变区间阈值法和Tennant 法的生态缺溢水量较低；在相同生态缺溢水量的条件下，将曲线按趋势延展，变区间阈值法的发电量较大。综合考虑变区间阈值法对实际生态优化调度具有可行性的参考价值。

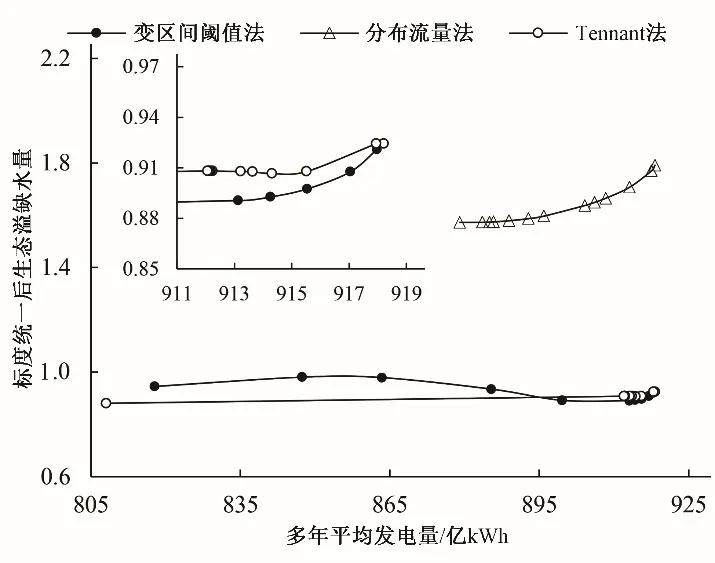
图3 统一标度后的各方案Pareto最优解Fig.3 Pareto optimal solution of each scheme after unified scale

2.3 不同方案下水库运行结果分析

为了进一步比较各方案下不同的生态需水约束对水库运行的影响，本文构建多目标调度模型进行验证，选取典型年绘制其流量过程线和水位过程线，其中生态权重为0.3（所有权重等价故任取一权重分析）。典型年的选取考虑河流的天然水文情势变化，对1952-2012年的年均入库流量进行频率计算，按15%、50%和85%保证率选取丰（1983年）、平（1957年）、枯（2009年）3 个典型代表年。图4、5 为典型年各方案逐旬的出库流量过程线和水位过程线。

2.3.1 典型年流量过程

水库典型年逐旬出库流量和水位的变化过程如图4、5 所示。从水库的出库流量过程（图4）可以看出，各方案的差异主要体现在枯水期。在枯水期，变区间阈值法和分布流量法相比，前者在3、4月份（6～15 旬）的出库流量偏大，更贴近适宜生态流量下限，较有益于生态；而在丰水期前的4、5月份（12～18旬）是鱼类产卵的高峰时期［22］，和Tennant 法相比，变区间阈值法和分布流量法的出库流量明显较大，有利于营造鱼类产卵所需的脉冲流量生境。此外，Tennant 法的出库流量一直较大，弃水风险较高，不利于水电站的经济运行。

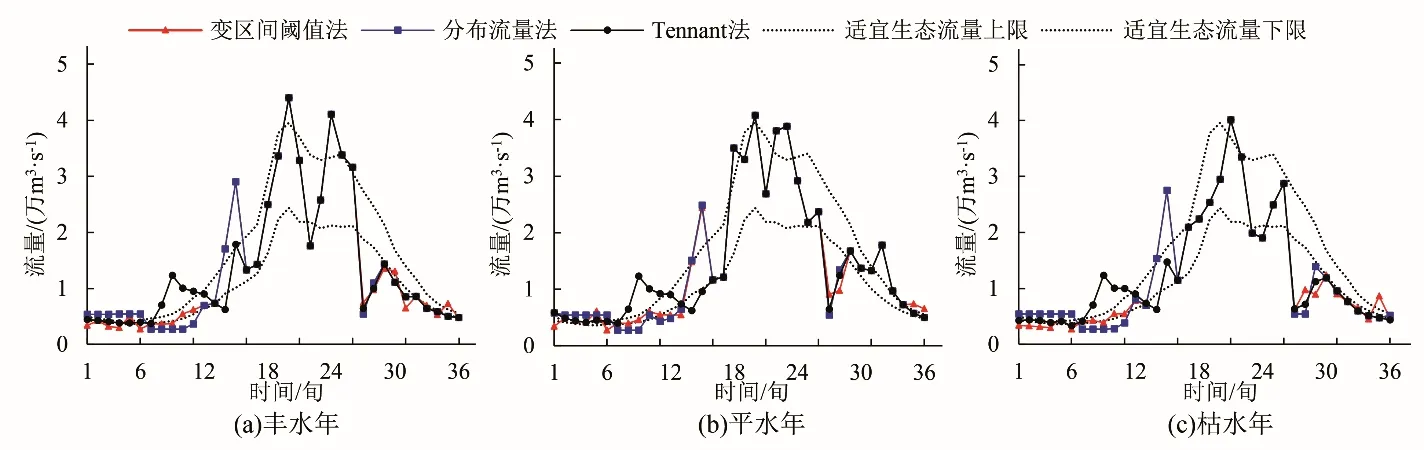
图4 典型年逐旬出库流量过程Fig.4 Process of outbound flow process per ten days in a typical year

2.3.2 典型年水位过程

由水库的水位过程（图5）可以看出，3种方案的差异主要体现在枯水期。在枯水期（1～18旬、27～36旬），变区间阈值法和分布流量法较Tennant 法而言，水库水位长期维持在高水位，有利于发电；并且变区间阈值法在2月份（6～9 旬）的水位有所下降，可以增大在长江最枯水期抵御咸潮入侵的作用，同时提高发电量。综上所述，变区间阈值法在特征时期的生态效益和发电效益等方面优于分布流量法和Tennant法。

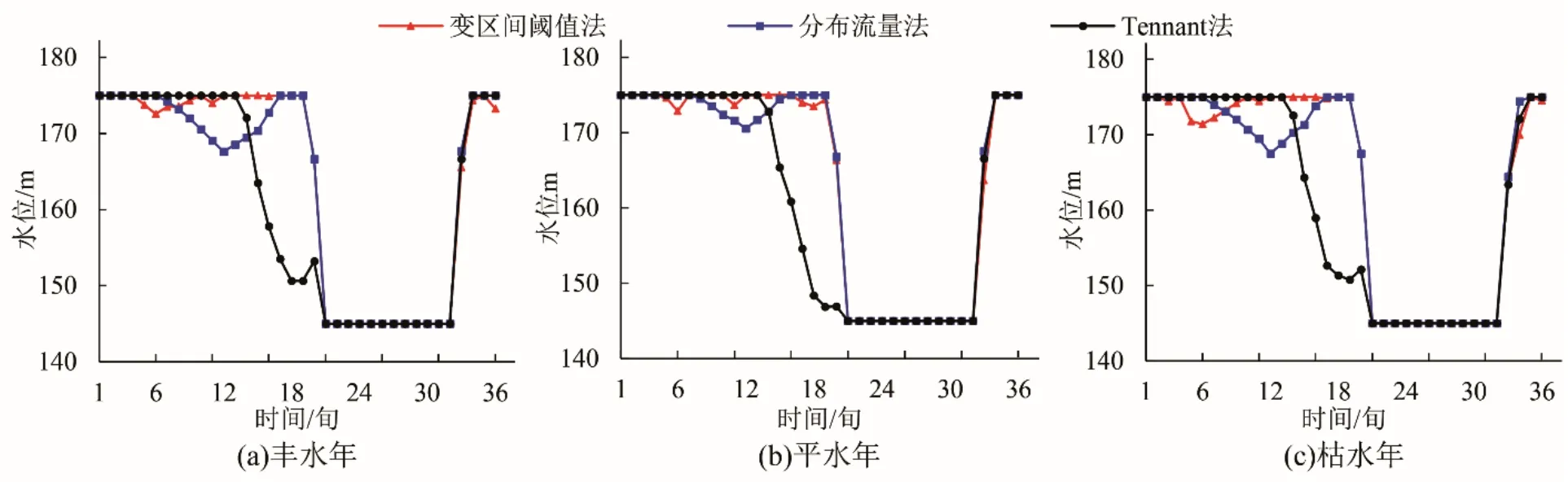
图5 典型年逐旬水位过程Fig.5 Process of water level process per ten days in a typical year

3 结 论

本文提出了考虑年内丰枯变化的生态需水计算方法：变区间阈值法，并与Tennant 法和分布流量法两种生态需水计算方法进行对比分析。通过构建以发电量最大和生态缺溢水量最小的多目标生态调度模型和实例分析，验证了所提方法的合理性和有效性。主要结论如下：

（1）与传统水文学法相比，变区间阈值法在枯水期简化计算量的条件下，展现出了不弱于分布流量法的调度结果，同时非劣解集的分布比Tennant法更加均匀；

（2）使用本文所提方法的调度结果中，在2月份水位有所下降，有利于抵御咸潮入侵；在3-5月份出库流量较大，有利于生态环境和鱼类产卵期产卵。

本文所提方法通过在枯水期仅设定下阈值简化了计算过程，在丰水期设定区间阈值又考虑了适宜生态需水的要求，为生态需水计算提供了技术方法和参考依据。