基于贝叶斯网络BOA算法进化计算的优化研究

陈福林

（赣州师范高等专科学校，江西 赣州 341000）

0 引 言

目前，社会各领域中，存在大量的优化问题。对于这些问题，如何进行优化，有不少研究人员进行了相关的研究，并提出了很多研究算法。本文在分析现有优化算法的基础上，进行了基于贝叶斯网络的进化计算优化研究。基于贝叶斯网络的进化估计计算研究首先是找好变量及各变量间的因果关系，根据变量间的因果关系构建网络模型，然后根据网络模型事件的因果关系的先验概率、条件概率来推导、优化问题解集的联合概率分布，用优解得到的联合概率分布优化下一代种群。基于贝叶斯网络的进化计算算法对解决高阶、多层次化的问题优化有很好的优势。在不确定性问题处理中得到较好应用。

1 进化计算

进化计算是一种以达尔文进化论为依据，对人工系统进行设计、优化和控制的技术和方法的总称。进化计算自从20世纪60年代提出到现在已经发展了4 个分支：一是由美国密歇根大学的J.Holland 提出的遗传算法，遗传算法在机器学习及系统优化等方面得到广泛应用；二是由美国科学家L.J.Fogel 提出的进化规划，该方法最初是用来预测符号系列输入的有限状态，后来用于优化问题的参数；三是由德国科学家RecHechenber 和Schwefe 提出的进化策略，该策略主要用来解决弯管形状优化问题；四是科学家Koza 提出的遗传程序设计，主要用于机器学习等，目前正尝试用于对C 计算机结构化程序设计言，C++程序设计语言、java 程序设计语言及Python 程序设计语言等面向对象程序设计语言进行优化学习，并对这些语言的算法优化取得了不错效果，在实际程序编写及项目开发中取得了应用。

2 遗传算法分析

遗传算法是一种随机优化算法，是通过对染色体的评价和染色体中基因的作用，有效地利用原有的信息来指导搜索，用搜索的信息改善优化质量状态，通过种群不断优化，得到最优后代。

遗传算法是一种依赖人工选择和重组操作的优化算法。在用遗传算法进行种群优化过程中要用到积木假设及模式定理，但积木假设及模式定理往往是相互矛盾的，因此在优化过程中经常达不到要求。

3 贝叶斯网络概述

贝叶斯网络又称为信念网络、概率网路、因果网络或知识图，从这些称呼可知，贝叶斯网络是用于描述变量间概率关于的图形模式，图中的节点即为变量，节点间的有向边表示变量间的因果关系，如图1所示，图1不仅能体现高度相互影响的变量集的直观界面，还能体现导致有效算法的数据结构，为复杂性和不确定性问题的解决提供了很直观自然的方法，用贝叶斯网络进行不确定性问题推理时用到事件即变量的先验概率及条件概率，推导出事件后验概率，从而找出问题的最优解，用的推理法为概率推理法，在给定一定的证据节点条件下计算查询节点的后验概率分布。

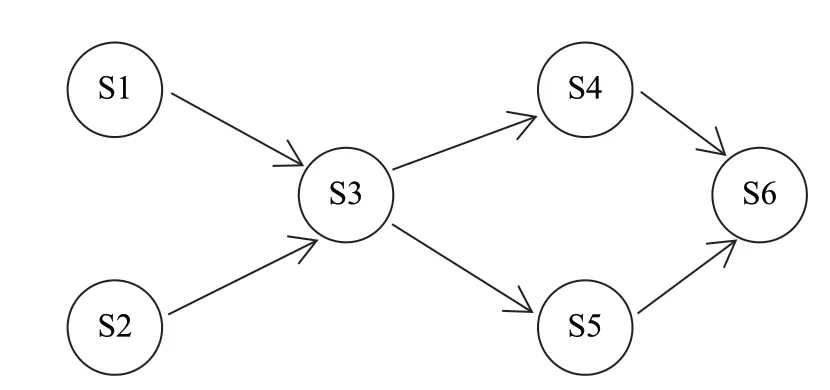
图1 贝叶斯网络模型图

4 基于贝叶斯网络进化计算优化研究

4.1 基于贝叶斯网络进化计算优化算法的实现思想

遗传算法可以理解为是在没有先验知识的情况下，从个体中学习基因之间的关系及个体的适应度信息，利用学习得到的信息产生更好的下一代群体的算法。前面分析了遗传算法中的积木假设及模式定理往往是相互矛盾的，且积木块往往又是分布在所有的染色体中，有时用遗传算法进行问题的研究时找不到最优解，在基于遗传算法研究的基础上引发了对分布估计算法的研究，分布估计算法又称为遗传算法的概率图模型方法，而贝叶斯网络进化优化算法是概率图模型中典型的一种模型优化算法。

贝叶斯网络进化优化算法的实现思想是使用图形作为工具描述因子间的因果关系，概率表述每一代群体的相互关系紧密程度，算法的基础是利用每一代的个体，从中学习随机变量的分布，在学习得到的分布基础上，生成下一代新个体，如此反复直到产生最佳群体，即最优解。

当我们用贝叶斯网络进化优化算法对问题进行优化时考虑的主要问题有两个方面：一是如何利用可选解进行估计，即如何确定先验概率；二是如何利用分布函数确定新解，即确定后验概率。这两问题互相关联，在优化问题的过剩中，如果能对初始分布进行正确估计，则能产生更好的优化解，对问题进行更好的优化。根据算法在实现时设计的不同，贝叶斯网络进化优化算法分为连续的贝叶斯网络进化优化算法和离散的贝叶斯网络进化优化算法。

4.2 贝叶斯网络优化算法流程

在BOA 算法中，首先通过均匀分布随机产生方式得到第一代群体。然后利用贝叶斯网络的结构学习中用到的评价函数探索空间网，构造一个与当前群体优秀个体相匹配贝叶斯网络，新的个体可从贝叶斯分布网络优化、推导产生，然后再用网络优化、推导产生新个体替代前一代中存在问题的个体加入种群。具体的算法流程如图2所示。

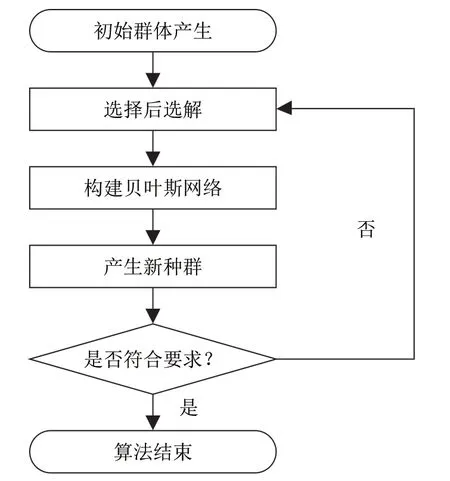
图2 概率图模型进化分布算法实现图

BOA 算法是贝叶斯网络作为变量的概率模型。用BOA算法进行问题优化时，要解决两个问题：一是评价函数的选择；二是如何对构建的网络进行采样。

4.3 BOA 算法的评价函数

在Cooper 及Buntine 等人研究的基础上，Heckerman 提出了贝叶斯网络的BDe 函数评价方法。利用BDe 进行贝叶斯网络结构学习，就是寻找后验分布最优的贝叶斯网络结构。即：

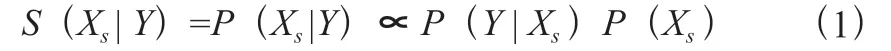
从公式可以看知，要计算一个X的Dbe 测度，必须计算实例数据的似然分布（X |）和结构的似然分布（X ）。如果实例数据完整，实例变量互相独立以及参数变量为Dirichlet 分布的假设情况下，BOA 算法的Bde 度量公式为：

式中：为背景信息；（|）为构建网络的先验概率；π为x的父亲节点集合；m′（ π）与m′（x，π）分别为优化问题的先验信息。在对问题进行优化时，把m′（x，π）与（|）融入到问题的优化中，先验概率反映出了被测量网络与先前网络的相似程度。

4.4 BOA 的采样算法

在给定了BOA 算法的评价函数后，接下来是事情就是根据现有的网络结构产生新的后选解，后选解要通过对构建的网络采样取得。BOA 算法的采样分两个步骤完成：一是确定节点间的关系，主要是确定网络结构中所有节点的祖孙关系，一般是通过排序算法来实现；二是根据步骤一确定的节点关系，产生一个新的后选解。因此具体算法为：

(1)根据给定的网络和群体，计算网络中每一节点对于父节点的条件概率。

(2)对网络中的所有节点进行排序，确定相应节点的父节点，置父节点到该节点的前面。

(3)按照先前的排序和计算得到的条件概率，依次采样每个节点。

(4)把所有采样得到的节点值合在一起，构成一个新的个体。

4.5 BOA 算法进化优化仿真过程

基于贝叶斯网络的进化计算优化仿真过程如图3所示。

图3 基于贝叶斯网络的进化优化仿真过程图

从基于贝叶斯网络的进化优化仿真过程图可知，用BOA 算法进行进化计算优化的关键是寻找度量值最大的网络来估计联合概率分布（）,首先选择种群D（）中构建贝叶斯网络模型，接着是对模型进行学习，模型的学习包含两个方面：一是结构的学习；另一方面是条件概率表的更新学习。新模型的学习在进化过程中是一个反复的过程，新的网络模型构建完后，新的个体可以对网络抽样得到。

5 结 论

利用贝叶斯算法进行进化优化时，是利用变量的联合概率分布来生成新的候选解，用贝叶斯网络构造数据模型，生产子代指导对解空间的搜索。BOA 通过对贝叶斯网络的学习和采样取代了传统遗传算法的交叉和变异操作，实现了对种群的学习并产生了优良的子代群体，同时避免了大量人工参数的设置、重要构造块的破坏。