基于高斯过程的人体步态关节力矩估计

李斯绮，张宇玲，杨建涛

上海理工大学康复工程与技术研究所，上海市 200093

0 引言

在下肢假肢、类人机器人和腿部外骨骼的开发设计中，人体步态数据极为重要，通过动作捕捉系统获取人类的步态数据，建立运动学、动力学模型，并设计合适的控制器，使它们能够跟随人体的步态轨迹[1]。但是，目前下肢外骨骼辅助等设备的控制技术有待进一步完善，这也是限制外骨骼等设备真正应用的主要原因[2]。由于人体自然步态的关节力矩会不断地、潜意识地调节[3]，所以解决控制问题的关键就是如何精确估计关节力矩。

关节力矩估计属于运动意图识别[4]。识别运动意图，获取准确的关节力矩，对于优化外骨骼助力机器人的控制、提高助力效果有着重要意义[5]。葛祎霏[6]采用拉格朗日方法进行动力学建模，确定下肢关节角度与力矩之间的关系，在此基础上进行控制系统的设计；Zhang 等[7]将所需的力矩作为时间的函数，控制行走时的踝关节外骨骼；张铁等[8]提出基于卡尔曼滤波的关节力矩估计方法，提高机器人控制的可靠性。

现有的方案主要分为离散技术和连续方法两种。离散技术将正常步态周期分成几个相位，通过识别步态相位，设计与步态相位同步的高级控制器[9]。由于人体关节力矩是连续变化的，所以连续运动估计显得更有价值[10]。这就需要一个实时精确且强鲁棒的模型来连续地估计关节力矩。

为了研究人体步态，一些研究者试图建立肌肉骨骼系统的生物力学模型[11]，一般将表面肌电信号作为模型的输入。Hill 等[12]提出的肌肉纤维收缩运动是该模型的理论基础，之后许多研究者基于Hill 肌肉骨骼模型或对其简化，进行关节力矩的估计。然而，Hill模型的性能受时变参数的限制，必须有效地辨识人体生理参数才能实现其准确性[10]。此外，该模型标定的工作量也很大，这些缺点阻碍其广泛应用。尹逊锋[5]为神经肌肉骨骼模型增加基本假设，建立了简化模型，并利用表面肌电信号和惯性元件估计人体下肢运动关节力矩。由于Hill 肌肉模型中需要的输入变量不易测得，熊保平等[13]建立人体关节力矩智能预测输入-输出关系的数学模型，确定了关节力矩智能预测的输入变量，从而实现关节力矩的智能预测；秦菲菲等[14]基于Udwadia-Kalaba 理论对下肢模型进行简化，提出了新的关节力矩分析方法，通过对等效模型的约束力求解分析关节力矩。

人体的每个子系统和环节中都有一些可测得的状态变量描述人体步态[4]，包括表面肌电信号、关节角度、地面反作用力和脚的姿态角度。高精确度估计的一个核心困难在于确定一个能够捕获生物信号背后动态信息的模型。

本文提出一种基于高斯过程的数据融合方法[15]，用于人体步态的关节力矩估计。该模型可以挖掘关节角度和力矩之间的深度内在的自然关系，性能优越。高斯过程的统计性质能够为控制器设计进行风险评估。

1 方法

人体步态的关节力矩估计很复杂，包括肌肉骨骼动力学、韧带力和骨之间的作用力[16]。

高斯过程是一种融合核函数和贝叶斯方法的机器学习方法，可用于处理非线性问题[17]。核函数将原始空间中的向量作为输入向量，并返回转换后的数据空间中向量的点积的函数。核函数是一种基本函数，常见的有常数核函数、平方指数(Squared Exponential Kernel,SE)核函数、Matérn 核函数族、白噪声核函数等。其中，SE核函数适用于平滑的动力学模型，并可将全局相关转化为局部相关，公式如下。

贝叶斯方法是统计学一种基本的方法，能有效地处理复杂的建模问题。它利用先验知识，结合当前数据，更新未知参数，从而得到后验概率。包含参数的后验概率密度如下。

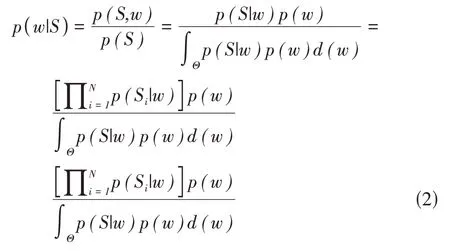
其中p(S|w)为似然函数，p(w)表示参数的先验概率密度函数，p(S)是关于输入输出数据的标准化常量。该公式中所有项只与参数w 有关，排除参数无关信息后得到更为有效合理的统计推断。

高斯过程完全由它的均值函数和协方差函数(即核函数)决定[18]，记为：

式中m(x)为均值函数，k(x,x')为协方差函数，其定义如下。

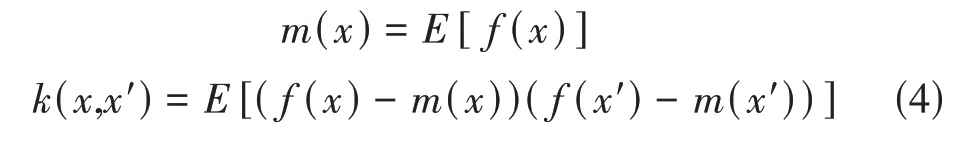
通过均值函数和核函数以及已知数据即能推导出预测值的分布函数。由此，在高斯过程建模时，选择合适的均值函数和核函数尤为关键。采用SE 核函数，用极大似然估计法求未知超参数，利用共轭梯度法对超参数进行优化，使似然函数的概率最大化。似然函数对超参数的偏导数：

其中∑=K(X,X)+，trace 表示矩阵的迹。确定核函数中的超参数之后，可以计算出预测点处的概率分布。

2 试验研究

1 位没有肌肉骨骼或神经功能障碍的受试者在参与试验前给予书面的知情同意，利用Vicon 光学动作捕捉系统和测力板验证所提出的方法，将16个标记点(直径10 mm)固定在受试者的下肢上，下肢的关节角度可以通过光学动作捕捉系统捕捉标记点得到。每只脚的地面反作用力/力矩则用测力板测得，通过逆动力学分析行走时的关节力矩。采样频率100 Hz。

受试者经过短暂练习后，在跑步机上以0.8 m/s的速度行走，进行4 次试验。随机取1 次试验数据作为训练集，其余试验数据作为测试集。在预测右侧关节力矩时，左腿的关节角度作为模型的输入；同样，预测左侧关节力矩时，右腿的关节角度作为模型的输入。利用均方根(root mean square,RMS)值和r2值判断估计效度。r2＞0.8为合理的估计值[19]。

3 结果

大部分预测的期望值都落在置信区间内。见图1。预测值和实际值的r2值见表1。在9 个值中有8 个＞0.8，大约22%的r2≥0.95。提出的算法可行。

图1 关节力矩估计结果

表1 0.8 m/s步速下的r2值

RMS 误差的最大值约为0.16 N·m/kg，最小值约为0.04 N·m/kg。试验精度足够高。见图2。

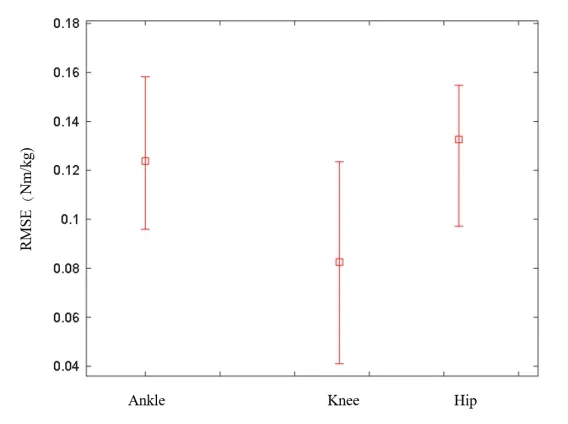
图2 特定速度下的RMS误差

4 讨论

算法必须在模型的精确性和复杂性之间作出平衡。这可以用贝叶斯信息准则来解决。前期研究成果表明[20]，高斯过程在关节力矩预测方面有比较好的泛化能力。本研究在此基础上，进一步研究通过关节角度预测关节力矩的可行性。在实际应用中，可以通过采集大范围人群的关节角度与关节力矩数据，通过大规模数据集训练模型，使模型具有广泛适用性。

此外，任何信息中都可能包含噪声。在某些特殊情况下，数据需要滤波处理。通过增加速度信息或通过融合表面肌电信号可以改善试验结果，是后续的一个研究点。

本文提出了一种基于高斯过程的人体步态关节力矩估计模型，该模型可以挖掘关节角度和力矩之间的深度内在的自然关系。试验结果验证所提出的数据融合模型在关节力矩估计方面的精确性，估计结果基本可靠。这对构建下肢外骨骼与类人机器人的高级控制器具有重要意义。

利益冲突声明：所有作者声明不存在利益冲突。