氦等离子体喷涂中发射光谱参数的研究

寇元哲, 李向富

（陇东学院机械工程学院，甘肃庆阳 745000）

0 引言

在宇宙中，等离子体是物质存在的主要形式，占宇宙中可观测物质总量的99%以上。其成分包括自由电子、束缚电子、离子、原子、分子，以及它们组成的束团。通常根据库仑耦合强度Γ和电子简并参数γ对等离子体进行分类。Γ≤1和Γ≥1分别表示弱耦合等离子体和强耦合等离子体，γ≤1和γ≥1分别称为经典等离子体和量子等离子体。多年来，人们已发展了多种理论模型和方法用于描述等离子体及其特性。例如，有限温度密度泛函理论[1]、从头计算分子动力学方法[2]、含时密度泛函理论[3]、蒙特卡罗分子动力学方法[4]、量子动力学理论[5]和量子蒙特卡罗模拟[6]等，这6种模拟方法精度较高，但计算量较大。为此，人们也发展了较为简单的解析模型，尤其是考虑等离子体对原子或者离子的屏蔽效应时，一般采用屏蔽势模型。目前，较为成熟的屏蔽模型是德拜模型、离子球模型和余弦德拜模型等静态屏蔽模型。德拜模型用于描述热动能项占据主导地位的弱耦合等离子体的屏蔽效应。对于库仑作用占据主导地位的强耦合等离子体，用离子球模型和余弦德拜模型描述。

热喷涂是一种表面改性和改良技术，在基体表面上沉积耐磨、耐蚀、耐热、绝缘、隔热、密封等各种功能涂层，还被广泛用于缺损零部件的修复。等离子体喷涂是热喷涂技术中应用最为广泛的一种方法。目前，等离子体喷涂技术己被广泛应用于运载工具的加工制造过程中，如航空航天、机械制造及机车车辆等领域[7]。例如，等离子体喷涂Al2O3、Cr2O3、Ti2O2等陶瓷粉末制备涂层，一方面可使零部件具有优异的耐磨性，同时还兼具有高的硬度，而且涂层的摩擦因数低、能耗小，在机械、航空等领域应用广泛[8]。发射光谱测量法是研究等离子体射流特性最重要的方法之一，目前已得到广泛应用。采用发射光谱诊断技术可以获得大量有关等离子射流特性的信息，而对等离子射流本身不会产生干扰，这些信息包括各种原子和分子的基态、激发态、电子的温度、电子的数密度和重粒子的温度等[9]。

在等离子体喷涂中，离子处在自由电子和带电离子所产生的势场中，不能再当做孤立自由离子处理。因为等离子体环境使得离子的诸多性质发生了变化，如谱线移动、谱线展宽、谱线合并、能级交叉和跃迁参数变化等[10]。通过对这些独特性质的测量或者计算可以确定等离子体的状态（如密度、温度等），为等离子体喷涂的精确调控提供依据[11]。宋鹏等[12]采用发射光谱法对大气压氦气等离子射流的活性粒子种类、电子激发温度、电子密度进行了诊断。林威等[13]采用一维包含蒙特卡罗碰撞的粒子模拟方法，对大气压氩气、氦气非热平衡等离子体射流电子能谱作了比较研究。

就我们所知，有关氦等离子体喷涂中发射光谱参数随等离子体屏蔽长度变化规律的研究还很少。本文采用相对论方法结合德拜屏蔽模型研究了氦等离子体喷涂中类氢氦离子发射光谱对应的跃迁能、跃迁概率和振子强度等光谱参数随德拜屏蔽长度的变化规律，并拟合出跃迁能、跃迁概率和振子强度与德拜屏蔽长度间的解析关系式，将为氦等离子体喷涂中的等离子体状态诊断提供指导和参考数据。

1 计算方法

对于单电子原子，其狄拉克-库仑哈密顿量的表达式为

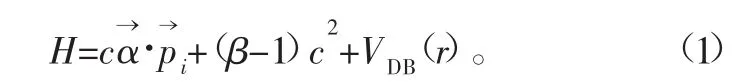
式中：右边的前两项表示束缚电子的相对论动能；VDB（r）的表达式见式（2）。

在总哈密顿量中包含了核电荷、束缚电子和自由电子的贡献之和，单电子的波函数可以通过自洽迭代的方法求解。在等离子体喷涂中，等离子体密度相对较低，适用于德拜模型描述周围等离子体对中心离子的屏蔽效应。德拜模型的主要思想是：假定一离子处在原点r=0处，核电荷数为Z，其周围的静电势适用于德拜模型描述，静电势表达式为

式中，D为德拜屏蔽长度，其表达式为

式中，Te和ne分别为等离子体中的电子密度和电子温度。

因为本文研究的是类氢氦离子，只有一个束缚电子，所以无需考虑等离子对电子-电子的屏蔽效效应。将式（2）所示的德拜屏蔽势以程序的形式替换相对论原子结构计算程序Grasp2K[14]中的核-电子间的纯库仑势程序，便可以用改进后的Grasp2K程序计算等离子体喷涂中的类氢氦离子的发射光谱参数。

本文所计算的光谱参数包括跃迁能、跃迁概率和振子强度。跃迁能指的是发生跃迁的初态（能量较高的原子态）和末态（能量较低的原子态）间的能量差值，本文中的跃迁能单位用波数（cm-1）表示。跃迁概率指的是单位时间内，电子从能量较高的原子态跃迁至能量较低的原子态的次数，单位为每秒（s-1）。跃迁概率可以分别用长度规范和速度规范来计算。电偶极跃迁概率的长度规范和速度规范下的表达式分别为：

振子强度是表征原子吸收或发射光子的重要物理参数。经典电动力学把辐射或吸收的基本单元看作是谐振子。原子中电子的跃迁引起电磁波的发射或吸收是由谐振子作简谐运动引起的。在确定的谱线内，通常用等效的振子数表达一个原子的吸收作用，这个数就叫作振子强度。振子强度同样可以分别用长度规范和速度规范来计算。电偶极振子强度的长度规范和速度规范下的表达式分别为：

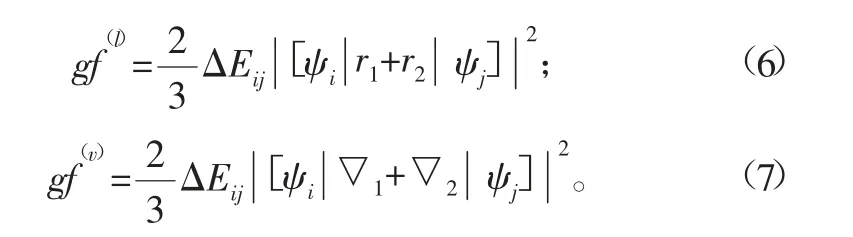
振子强度gf 为一无量纲的代数量。从式（4）～式（7）中可以看出：跃迁概率和振子强度分别正比于跃迁能的三次方和一次方，二者都与线强度成正比。通过比较长度规范下和速度规范下线强度S、跃迁概率A和振子强度gf 的计算结果，可以判断计算结果的准确度。但在实际计算中，二者的结果只可能非常接近，一般情况下不可能完全一致。速度规范下的计算结果对波函数的精度要求非常敏感，波函数的较小变化便会引起计算结果的较大变化；而长度规范下的计算结果对波函数的精度要求较低，计算结果较为稳定；所以我们一般情况下推荐使用长度规范下的计算结果。本文所计算的长度规范下的跃迁概率和振子强度数值与速度规范下的跃迁概率和振子强度数值几乎完全一致，所以本文的计算结果非常准确。本文中列出的跃迁概率和振子强度均为长度规范下的数值。

2 结果与讨论

表1所示的是自由类氢氦离子1s-2p和1s-3p的跃迁能和跃迁概率，Diff1%表示本文所计算的跃迁能与美国国家标准与技术研究院NIST[15]推荐值的相对误差，Diff2%表示本文所计算的跃迁概率与美国国家标准与技术研究院NIST[15]推荐值的相对误差。从表1中可以看出，本文所计算的自由类氢氦离子1s-2p和1s-3p的跃迁能与NIST推荐值的相对误差均为0.0149%，所计算的自由类氢氦离子1s-2p和1s-3p的跃迁概率与NIST推荐值的相对误差分别为0.0060%和0.0004%。由此可以看出，本文所计算的跃迁能和跃迁概率分别与美国国家标准与技术研究院NIST的推荐值符合得非常好。所以本文所选取的计算方法是非常可靠的。

表1 自由类氢氦离子1s-2p和1s-3p的跃迁能和跃迁概率

表2所示的是等离子体喷涂中不同等离子体密度和温度对应的不同德拜屏蔽长度下，类氢氦离子1s-2p、1s-3p的跃迁能、跃迁概率和振子强度。通过跃迁能可以直接求得发射光谱的波长，跃迁概率和振子强度与发射光谱的强度直接相关，故表2所示的数据对于氦等离子体喷涂有着重要的参考价值。从表2中数据可以看出：随着德拜屏蔽长度D的减小，1s-2p、1s-3p的跃迁能、跃迁概率和振子强度均逐渐减小。这是因为随着德拜屏蔽长度D的减小，对应的等离子体屏蔽强度逐渐增大，原子核对束缚电子的库仑引力逐渐减小，故辐射光谱对应的跃迁能、跃迁概率和振子强度均逐渐减小。

表2 等离子体喷涂中，类氢氦离子1s-2p、1s-3p的跃迁能、跃迁概率和振子强度

图1（a）～图1（f）分别表示类氢氦离子1s-2p、1s-3p的跃迁能、跃迁概率和振子强度的对数随德拜屏蔽长度的对数的变化曲线。从图中可以看出，1s-2p、1s-3p的跃迁能、跃迁概率和振子强度的对数随德拜屏蔽长度的对数的变化规律完全相似。分别对图1（a）～图1（f）的曲线做了指数型曲线拟合，从图1（a）～图1（f）可以看出，拟合曲线与计算曲线符合得非常好。拟合的表达式为

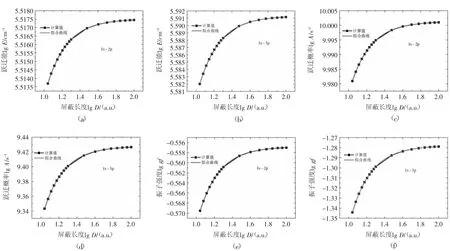
图1 类氢氦离子1s -2p、1s -3p的跃迁能、跃迁概率和振子强度的对数随德拜屏蔽长度的对数的变化曲线

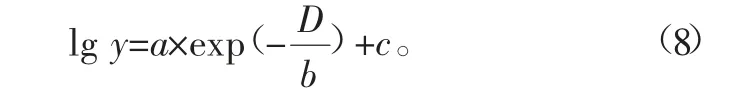
说明：D表示德拜屏蔽长度，x（y）表示x×10y。

式中：D为德拜屏蔽长度；a、b、c为通过拟合所确定的常数；y为拟合的目标变量，即分别表示跃迁能E、跃迁概率A和振子强度gf的对数。常数a、b、c的值如表3所示。

表3 1s-2p和1s-3p的跃迁能、跃迁概率和振子强度的拟合表达式中的参数值

3 结论

本文采用相对论方法结合德拜屏蔽模型计算了等离子体喷涂中类氢氦离子发射光谱对应的跃迁能、跃迁概率和振子强度等光谱参数。结果表明：类氢氦离子1s -2p、1s -3p的跃迁能、跃迁概率和振子强度均随着德拜屏蔽长度的减小而逐渐减小。精确地拟合出了跃迁能、跃迁概率和振子强度的对数与德拜屏蔽长度对数间的解析关系式，从而可以求得任意德拜屏蔽长度下类氢氦离子1s-2p、1s-3p的跃迁能、跃迁概率和振子强度，这对于等离子体喷涂中关于密度和温度的诊断有着重要的参考价值。