基于RANS法的螺旋桨敞水性能预报方法研究

邱鹏， 何钰璋

（武警海警学院，浙江宁波 315801）

0 引言

螺旋桨是当今船舶行业运用十分广泛的一种推进器，而螺旋桨的敞水性能的准确预报对船舶快速性等性能研究起着至关重要的作用。目前，螺旋桨的性能研究途径主要分为试验方法、理论预报方法及CFD技术。螺旋桨敞水性能试验方法虽然研究手段成熟、研究结果可靠，但是试验消耗成本较大，工序繁琐，因此在性能优化等方面研究明显感觉阻力较大。理论预报方法研究中，大部分学者均忽略黏性问题，采用势流理论进行预报，这虽然简化了计算过程，但是计算精度有待提高。当下，随着CFD技术的快速发展，通过求解RANS方程的方法已有效地应用在船舶性能数值预报中，该方法成本低、计算精度高，特别适用于螺旋桨性能的优化设计研究，目前得到了广泛应用[1-3]。

本文以DTMB P4119螺旋桨为研究对象，对其二维坐标进行转化，导入UG中进行三维建模，运用STAR-CCM+自带的非结构网格技术作网格划分，探讨网格密度与湍流模型对敞水性能的计算精度的影响，同时分析流场细节，验证所采用的计算方法的可靠性，为后期的螺旋桨水动力噪声等性能数值预报打下坚定的基础。

1 理论基础

1.1 控制方程

在数值研究中，对于介质流体假定为不可压缩，则流场的连续方程和动量方程分别为：

式中：ui、uj为速度分量；ρ为流体密度；μ为动力黏度。由于方程中Reynolds应力项为未知量，因此需要引进相应的湍流模型来封闭方程组。

1.2 湍流模型

1）标准κ-ε模型。

标准κ－ε模型引入了湍流耗散率ε方程：

结合湍动能κ决定湍动黏度μt，湍动黏度μt表达为ε和κ的函数：

在认为流体不可压缩的前提下和忽略用户自定义源项时，相应的输运方程表达形式为：

Gk为湍动能产生项，由平均速度变化引起，表达式为

根据实验验证，模型常数取值为：C1ε=1.44；C2ε=1.92；Cμ=0.09；σk=1.0；σε=1.3。

标准κ-ε模型一般适合运用于高雷诺数湍流，即湍流运动发展充分情况。一般而言并不适合运用在流线弯曲情况下。

2）RNG κ-ε模型。

RNG κ-ε模型中湍动能κ输运方程为

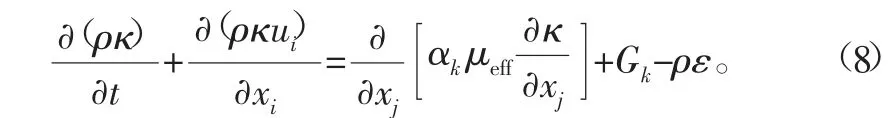
湍流耗散率ε输运方程为

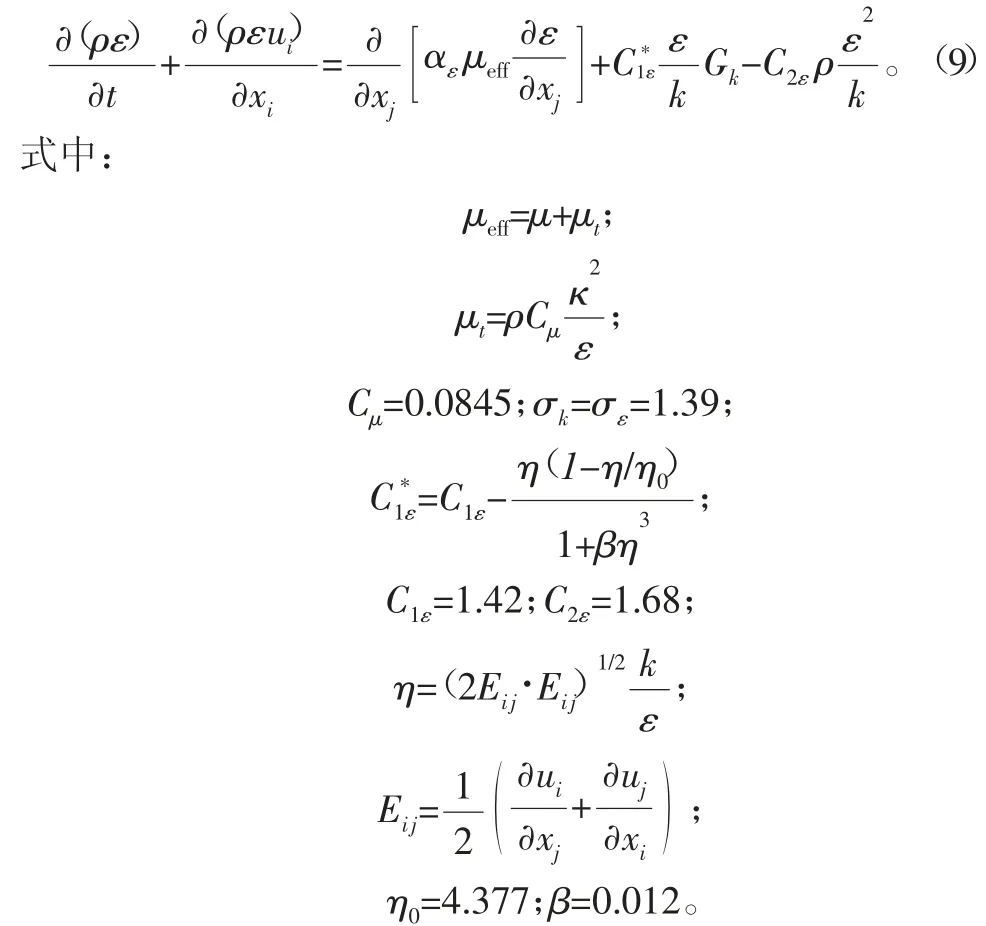
RNG κ-ε 模型考虑了旋转流动的情况，也可以更好地处理高应变率和流线弯曲较大的流动情况。

3）Realizable κ-ε模型。

Realizable κ-ε模型中湍动能κ输运方程为

Realizable κ-ε模型考虑到了流体旋转的相关情况，这是比标准κ-ε模型和RNG κ-ε模型优越的地方[4]。

2 数值模拟

2.1 螺旋桨三维建模

本文的研究对象采用DTMB P4119三叶桨，直径为0.3048 m，毂径比为0.2，盘面比为0.6，叶剖面为NACA66（MOD）。在三维建模时，采用汇编语言实现叶切面二维坐标型值点批量地转换为空间的三维坐标型值点，最后将三维坐标型值点以点文件形式导入到ICEM软件中进行回转体建模[5]，以半圆和圆柱代替桨毂，再导入到UG中进行实体封闭处理，三维离散型值点图和螺旋桨三维实体图如图1和图2所示。

图1 螺旋桨三维建模实体

2.2 划分计算域和网格

将螺旋桨放入无限大的静水域中进行模拟实验，计算域的静止外域为入口、出口、远场边界和除掉内部旋转域以外的部分所构成的计算空间，整个的计算域如图2所示。计算域的大小要满足流动充分发展，例如不受壁面和上游的干扰。选择的网格应在当前计算量承受范围之内，因此通过查阅文献[6-7]，最终计算域外域大小设定如下：速度进口距中心点距离为5D，压力出口距中心距离为7D，大圆柱直径为10D。在大圆柱体中取桨前0.4D，桨后0.6D，半径为1.2D的小圆柱体，所构成区域作为旋转域，两者结合则为整个计算域（其中D为螺旋桨的直径）。

图2 螺旋桨计算域示意图

本文运用STAR-CCM+的非结构网格对其进行网格划分，STAR-CCM+里面包含四面体、多面体和切割体网格3种体网格生成方法。本文选用了资源和内存都较优的切割体网格。在桨叶表面均匀划分网格并且对叶梢、叶背、导边和随边进行局部网格加密，桨叶和桨毂等物面部分采用3层棱柱层边界网格以模拟边界层流动，总体网格密度由旋转域到静止域逐渐减小，网格数目向外逐渐稀疏，网格划分如图3所示。

图3 螺旋桨面网格图

2.3 边界条件

将入口边界设为速度进口，根据进速系数输入不同的速度，将出口边界条件设为压力出口条件；远场边界设置为壁面条件，螺旋桨叶和桨毂设置为壁面条件；静水域和旋转域的交界面设置为interface；将整个旋转域设置成绕x轴做旋转运动，采用MRF模型进行旋转仿真运动；压力速度求解采用simple算法，计算时将螺旋桨转速设为定值10 r/s，只改变来流速度；进行迭代计算时，最大迭代步数设置为500步。

3 计算精度分析

在开展螺旋桨敞水性能数值模拟时，涉及的计算影响因素较多，例如三维建模的准确性、计算域的划分、网格密度、湍流模型的选取等。本文主要讨论网格密度和湍流模型对性能模拟精度的影响[8]。

3.1 定义场函数

对螺旋桨推力、转矩进行无量纲化处理，定义如下：

螺旋桨推力系数计算公式为

螺旋桨转矩系数计算公式为

其中：N为螺旋桨转速；D为螺旋桨直径；T为螺旋桨推力；Q为螺旋桨转矩；ρ为流体密度。

3.2 网格密度影响分析

在螺旋桨网格划分时，设置了桨表面的边界层网格，总高度设定为2 mm，通过改变边界层的网格层数，从而实现网格密度的增加。本文选取了4个网格数目，分别为216万、357万、486万、525万网格。湍流模型选择Realizable κ－ε，在其他条件保持不变的情况下，计算螺旋桨进速系数为0.5时的敞水性能，将计算结果与试验值对比，从而综合选取合适的网格尺度和数目，计算结果如表1所示。

表1 不同网格数目对敞水性能模拟影响分析

从表1可以看出，随着网格密度的增加，网格对计算信息的捕捉更加精细，并随着网格数的增加，计算误差逐步降低，在网格数为486万附近时，KT和KQ的误差百分比达到最小，当随着网格数目进一步增加时，计算误差又呈现出变大的趋势，这是因为网格过密的话，对应的边界层网格的Yplus值会超过选取的湍流模型的要求范围，造成边界层、湍流及实际流场的模拟偏离。

3.3 湍流模型影响分析

为了准确得到适用的湍流模型，在查阅相关文献[9]的基础上，分析3种不同湍流模型对计算结果精度的影响分析，此处3种计算方案只改变湍流模型，其余计算条件保持一致，选取上述网格数为486万为计算文件，分别采用标准κ－ε、RNG κ－ε和Realizable κ－ε湍流模型进行探讨，计算螺旋桨在同一进速系数J=0.5的推力和转矩大小。

由表2可以看出，RNG κ－ε和Realizable κ－ε两种湍流模型的计算结果相差不大，均能较为准确地模拟螺旋桨的敞水性征。而标准κ－ε湍流模型在对推力的预报方面表现较好，而对转矩的模拟误差很大，这可能是因为对于较大流线曲率的流动（如螺旋桨旋转流动等），流线的曲率会发生额外的应变，湍流扩散的强度也随之加大，因此采用这种湍流模型就不太适合此种模拟。采用RNG κ－ε和Realizable κ－ε湍流模型进行进一步的研究较为合适。

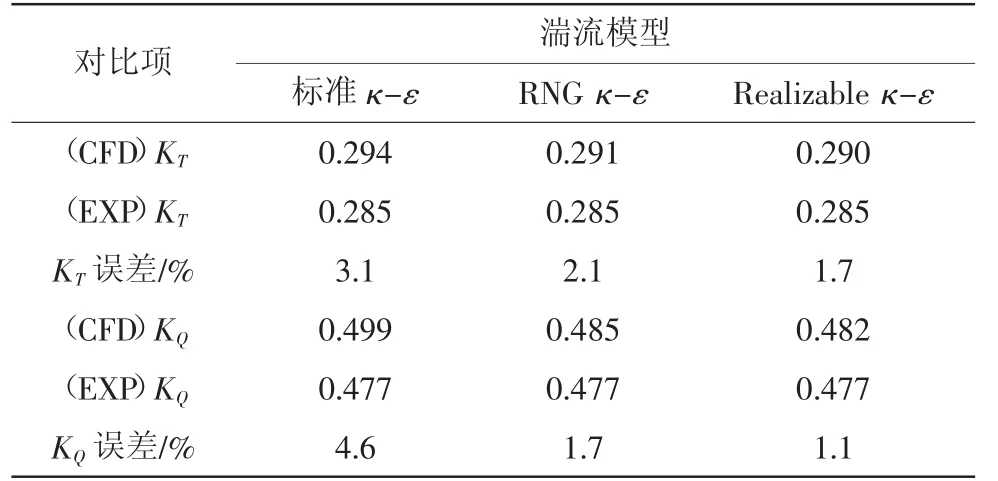
表2 不同的湍流模型对敞水性能模拟影响分析

3.4 性能曲线分析

借用以上的计算经验，采用网格数目为486万、湍流模型为Realizable κ-ε的计算方案，分别计算进速系数J为0.500、0.700、0.833、0.900、1.100的工况下DTMB P4119桨的敞水性能，并将其与试验结果相比较，计算结果如图4所示。从图4可以看出，进速系数为0.500～0.833时，敞水效率仿真值和试验值相差很小，在高进速系数时，误差较大，但均控制在10%以内，试验性能曲线和数值模拟曲线能够较好地吻合，验证了本文计算方法的可靠性，说明基于本文采用的数值模拟方法能够较好地预报螺旋桨的敞水性能。

图4 螺旋桨敞水性能曲线图

3.5 流场分析

以进速系数为0.5为例，分析螺旋桨的黏性流场云图，从细节处分析数值预报方法的可靠性。

观察图6、图7可知，在同一工况下叶面压力要远大于叶背压力，并且可以明显看出，压力由叶根到叶梢、由随边到导边逐渐增大。这与实际情况中的螺旋桨运动所产生的压力变化是一致的。

图6 螺旋桨叶背压力云图

图7 螺旋桨叶面压力云图

由图8的螺旋桨的Yplus值可知，大部分区域的Yplus值范围在30～200之间，在边缘附近的Yplus值比较小，这是由于网格较密所造成的，总体而言，由Yplus值的分布可知，本文所采用的网格划分方法是合理的，Yplus 值范围也在Realizable κ－ε湍流模型所要求的范围之内[10]。

图8 螺旋桨Yplus值图

4 结论

本文基于商业软件STAR-CCM+研究了不同工况下DTMB P4119桨的敞水性能和桨叶压力分布，考察了网格密度和湍流模型对数值计算精度的影响，计算结果与试验数据能很好地吻合，建立了基于RANS方程的螺旋桨敞水性能的预报方法，为今后更复杂的黏流问题（如空化、噪声等）研究提供了参考。