基于ANSYS的直列四缸发动机曲轴强度分析

王 乐，王立伟，赵飞鹏，梁健伟，王 洋

（西安石油大学机械工程学院，西安 710065）

0 引言

曲轴是发动机中最重要、承载最复杂的零件之一。其造价约占一台发动机总价的20%～30%，其使用寿命决定发动机的使用寿命[1]。在工作过程中，曲轴承受着气缸内的气体压力及往复和旋转质量惯性力引起的周期性变化载荷。这些扭转力矩和大小、方向不断变化的弯曲力，在曲轴内产生交变的弯曲及切应力，使曲轴发生疲劳破坏。当发动机开启之后，随着汽缸内的可燃烧的气体被点燃后，促使活塞在汽缸内作上下往复运动，进而带动连杆运动，最后使得曲轴作旋转运动。当发电机工作时，由于汽缸内的气体被周期性地点燃，从而使得负荷也作周期性地变化，负荷经过活塞和连杆的传递进而作用于曲轴之上。通常曲轴在承受这些应力时，其所面临的工作条件非常苛刻，曲轴的寿命及其强度等都会面临着及其大的挑战，因为，如果曲轴发生断裂，会发生不可估量的事故，造成不可挽回的损失。所以，在提高发动机的性能和它的可靠性时，曲轴就显得格外重要，必须要满足其使用要求才能进行下一步地安装和调试运行[2]。同时，在周期性变化的载荷作用下，曲轴可能在发动机转速范围内发生共振，加速曲轴的疲劳破坏。由于曲轴是发动机中典型的易损件之一，其强度和振动特性决定了发动机整体地可靠性，故此对曲轴进行有限元分析，研究其应力应变状态，进而知道其固有特性，对后面的调试和运行都有着极其重要的作用。

本文中通过利用以曲轴的做功轨迹图及其载荷为基础，通过利用SolidWorks软件建立曲轴的三维模型，并且通过Ansys软件内部的通道将其导入，进而分析曲轴的应力应变及其唯一变化规律，找出其受力的最大点及变形最严重的部分，并且对其进行总结归纳，为以后发动机曲轴的优化改进提供更重要的依据。图1所示为SolidWorks软件建立的曲轴及其缸体的立体模型。

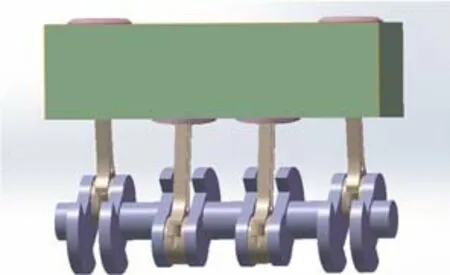
图1 直列四缸发动机曲轴实物

曲轴的基本结构如图2所示，主要由前端轴、主轴颈、连杆轴颈、曲柄、平衡重和后凸缘盘等部分构成。前端轴主要用来安装止推垫圈、启动抓和皮带轮等部件；曲柄用来连接主轴颈和连杆轴颈；平衡重的作用是平衡曲轴工作时产生的离心惯性力及其力矩；后凸缘盘用来安装飞轮等部件[3]。

图2 曲轴基本结构

1 直列四缸发动机模型建立

本文所研究的曲轴为某直列四缸发动机整体式曲轴，含有5个主轴颈、4个连杆轴颈、曲柄、平衡重、4个活塞和一个缸体。因为发动机曲轴及其活塞、缸体的结构极其复杂，使用ANSYS中的DM模块建模并非易事，因此采用专业的三维建模软件建立其立体模型，

2 曲轴结构参数

本文中曲轴材料为结构钢，具体结构参数如表1所示。

表1 曲轴结构参数

3 曲轴强度的有限元分析

3.1 建立有限元模型

本文中直列四缸发动机曲轴的材料均选为结构钢，它的密度是7 850 kg·m-3，泊松比为0.3，杨氏模量为2×1011Pa，拉伸屈服强度为2.5×108Pa，抗压屈服强度为2.5×108Pa。本曲轴模型是通过SolidWorks建立，然后导入Ansys软件中进行有限元分析。

3.2 添加运动副

通过在DM控制面板中添加转动副，分别约束4个连杆和连杆轴颈的转动副，同理按照相同方式，添加4个活塞与4个连杆的转动副；其次通过Translational命令添加4个移动副，分别约束4个活塞与缸体的移动副；再次通过Revolute命令添加曲柄的两个约束副，使得曲柄可以按照轴线旋转，带动连杆作旋转运动，进而带动活塞作上下往复运动；最后通过Fixed命令约束缸体的上表面，使得缸体固定。经过以上的操作，曲轴、连杆以及活塞、缸体之间的约束便建立完成，其运动副添加结果如图3所示。

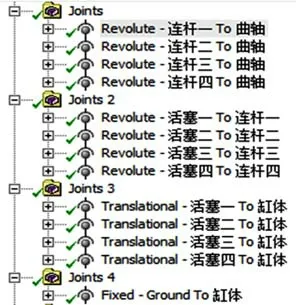
图3 运动副添加结果

3.3 划分网格

有限元网格划分是将整体模型结构离散化，是数值分析的前提，也是至关重要的一步，其直接影响着后续数值计算分析结果的精确性。一个良好的网格划分，不但可以保证分析结果的精度，同时也能够大大降低后期处理的计算量[4]。

本文采用ANSYS Workbench16.0中自带的Mesh模块对曲轴进行网格划分，网格划分尺寸为0.005 mm，其他设置均为默认选项，其结果如图4所示。ANSYS Workbench16.0是一个单独的工具平台，为ANSYS的不同求解器提供相应的网格文件。自14.0起，Workbench中可以直接划分网格。直接划分网格优点之一就是能单独地划分几何体的网格，而之前划分网格时只能整个极型同时起划分，显然直接控制网格划分具有更大的柔性[5]。网格划分之后的结果共包含13 301个单元，29 304个节点。

图4 网格划分结果

3.4 曲轴强度分析

曲轴在工作过程中承受的载荷及边界条件：主轴承支撑作用力、输出轴反扭矩、平衡块离心力、连杆轴颈和曲轴的离心力、连杆对连杆轴颈的载荷等。

对于直列四缸发动机，当活塞处于上止点位置时连杆轴颈载荷达到最大值，因此，只需考虑各个气缸分别处于压缩终点，活塞在上止点位置时的受力状态时即可。

本文中根据直列四缸发动机的最大扭矩转速，最大功率计算工况，由发动机动力学计算得，在点火上止点附近，由于爆发压力与活塞和连杆惯性的作用，使得连杆轴颈受最大得载荷。

按照动力学法计算载荷[6]，并假设作用在轴颈上的载荷为分布载荷，且根据有限宽度轴颈油膜压力应力分布规律，并忽略油孔处压力峰值突变的影响，采用以沿轴线均匀分布，沿圆周方向120°范围内呈余弦分布的载荷边界条件。

本文中所添加的Force力是分别作用于一、四、二和三号活塞的上表面，力的大小为：Step1-9 409.7 N；Step2-9 383.9 N；Step3-8 138.3 N。其次给曲轴添加一个转动Joint-Rotation，让其在1 s时转动10°，2 s时转动25°。

利用Workbench中自带的Bearing Load选项[7]，即轴承载荷。其径向分量将根据投影面积来分布压力载荷，轴向载荷分量沿着圆周均匀分布。由动力学计算可知，在点火上止点位置时由于气体爆炸压力与惯性作用使得作用于连杆轴颈表面，连杆轴颈所受的最小载荷为15 511 N。

Workbench中可通过力矩载荷或者力偶载荷添加力矩或力偶在任意实体表面，如果选择多个表面侧力矩或力偶[8]将分摊在这些面上，发动机工作时，由曲轴后端传出的扭矩，曲轴必然受到一定的扭转力，作用在曲轴前端和后凸缘盘上，根据公式，作用在曲轴上的最大扭矩可以近似为7.95×105N·mm。

Workbench中常用的支撑约束为Cylindrical，即圆柱面约束，可以施加在圆柱表面，并可以指定轴向、径向或者切向自由度的约束状况，但此约束通常仅适用于小变形线性分析[9]。在曲轴实际工作时，变形量很小，因此可以采用此种约束。本文所研究的曲轴为某直列式发动机整体式曲轴，含有5个主轴颈，并通过轴瓦、轴承安装在发动机箱体内，因此，5个主轴颈处可施加轴向和径向固定，切向自由的圆柱面约束。

4 仿真结果分析

在Ansys中，等效应力又可称之为Von Mises，其应力分量可以进一步转化仅仅显示法向应力的方式[10]。在Ansy结果分析中的"Von Mises Stress"，通常也会将它称之为等效应力，其遵循材料力学的第四强度理论[11]。而Von Mises Stress[12]也确实是一种等效的应力，并且用其应用应力等值线来表达模型里的应力的分布状态，可以清晰且准确地看出其在内部的变化情况，进而可以更快地找出并确定其危险区域处于哪一位置。总变形量Total Deformation指的是结构在荷载作用下产生的变形量[13]。经过以上对比分析，本文中采用最大等效应力分析。

一缸点燃时，曲轴的总变化量图和等效应力图依次如图5～6所示。同时，较大等效应力为75.4 MPa，处于一缸连杆轴颈与曲柄、主轴颈与均衡重的连接处，较大的变化量为0.020 167 mm，处于连杆轴颈与均衡重的边界处。

图5 一缸点燃时总变形量

图6 一缸点燃时等效应力

四缸点燃时，曲轴的总变化量图和等效应力图依次如图7～8所示。同时，较大等效应力为77 MPa，处于四缸连杆轴颈与曲柄、主轴颈与平衡重的连接，较大的变形量为0.020 307 mm，位于连杆轴颈与平衡重的边界处。

图7 四缸点燃时总变形量

图8 四缸点燃时等效应力

二缸点燃时，曲轴的总变化量图和等效应力图依次如图9～10所示。同时，较大等效应力为73.4 MPa，处于四缸连杆轴颈与曲柄、主轴颈与平衡重的连接，较大的变形量为0.020 158 mm，位于连杆轴颈与平衡重的边界处。

图9 二缸点燃时总变形量

三缸点燃时，曲轴的总变化量图和等效应力图依次如图11～12所示。同时，较大等效应力为73.1 MPa，处于四缸连杆轴颈与曲柄、主轴颈与平衡重的连接，较大的变形量为0.020 158 mm，位于连杆轴颈与平衡重的边界处。

图10 二缸点燃时等效应力

图11 三缸点燃时总变化量

图12 三缸点燃时等效应力

本文将有限元方法与3D建模相结合，完成了直列四缸发动机曲轴静态的强度分析。通过分析可知道运用这种方法可以节省时间，分析准确，方便快捷，对于后面的设计优化曲轴结构具有重要意义。

5 结束语

本文通过利用Solidworks软件建立直列四缸发动机曲轴的模型，利用Ansys Workbench软件进行曲轴的有限元静力学分析，最终得到曲轴在不同缸点火时2 s内的应力和位移变形云图[14-16]。通过分析对比可得当四缸点火时，会出现最大的应力值，该应力值为77 MPa，并且位于连杆轴颈的过渡圆角处，最大的变形量为0.020 307 mm；在三缸点火时，会出现最小的应力值，该应力值为73.1 MPa，最小的变形位移量为0.020 158 mm。因此可以推断出在曲轴连杆轴颈的过渡圆角处易发生疲劳破坏，在进行优化设计时应该时刻注意该区域，改善其应力应变。

本文创新性地将ANSYS软件与三维绘图软件Solid-Works相结合，不仅快速、便捷、准确，而且为后面曲轴的设计及优化提供了更加可靠而有效的一种方法，对优化其结构有重大意义。同时，通过分析可直接看出其所受的最大力，变形最为严重的地方处于何位置，对结构优化有重要的帮助。