码垛机器人的动力学仿真分析

陈修奇，李鹏飞，周永志

（1.珠海格力电器股份有限公司，广东珠海 519000；2.耐世特汽车系统亚太技术中心，江苏苏州 215000；3.苏州汇川控制技术有限公司，江苏苏州 215000）

0 引言

码垛机器人是现在物流、制造等行业迅速发展的一类工业机器人。其在码垛、搬运等领域效率高，适应性更强，在解决生产成本高，改善工人劳动强度等方面具有很大的价值和意义[1-2]。

虚拟样机技术，主要是对机械系统进行的运动学和动力学分析。通过轨迹规划动力学仿真，模拟机器人实际运行工况，获得相关理论数据，在实际样机开发过程中可大量缩减时间和成本，近年来得到了广泛的应用[3-4]。梁林坚等[5]利用牛顿-欧拉法得到动力学参数，利用ADAMS软件对重载码垛机器人进行刚柔耦合动力学分析，求出关节驱动力矩，验证前期驱动部件的选型。边兵兵[6]利用ADAMS和Ansys软件对机械臂进行刚柔耦合动力学仿真分析，得到不同工况下大臂的受力曲线和规律。朱华炳等[7]利用ADAMS建立了工业机器人的虚拟样机模型，仿真得出了机器人末端点运动的位移和速度曲线，证明数学模型的正确性。芮执元等[8]用ADAMS软件建立刚柔耦合模型仿真分析码垛机器人，通过后处理得到手腕末端点处的位移、速度和加速度图像，并与全刚体仿真分析结果进行对比。吕应柱等[9]运用SolidWorks及ADAMS对机器人进行了三维建模、运动轨迹规划和仿真分析，得出曲线验证了运动学推导的正确性。刘伟达等[10]利用ADAMS仿真验证所建立的驱动函数符合小型机器人的实际运行情况。

以上学者都采用了动力学软件做了仿真分析工作，但没有试验验证过仿真曲线结果的精确度。本文以负载能力180 kg的四轴码垛机器人为研究对象，运用Solid-Works软件建立码垛机器人的3D模型，将3D模型及其动力学参数，导入到ADAMS软件中，建立虚拟样机模型，再进行约束、驱动等设置，仿真输出各个关节的负载转矩，速度，加速度曲线，从而可获取减速机所受转矩以及电机驱动转矩。最后与实际样机测得的电机转矩数据进行对比分析，验证动力学仿真结果的精确性。通过此方法对于产品结构设计具有重要的指导意义。

1 码垛机器人整体结构和性能参数

此款机器人是自主研发负载能力180 kg的码垛机器人GR4180，由GR4180码垛机器人结构简图（图1）可知，它主要由底座、转座、大臂、小臂、手腕、大臂副杆、小臂副杆、三脚连杆、氮气弹簧、负载及其他零部件组成。该码垛机器人结构采用两组平行四边形连杆机构组成，第一个由转座、大臂、三脚连杆、大臂副杆组成，另一个由三脚连杆、小臂、手腕、小臂副杆组成，此结构可以使手腕末端法兰始终与地面保持水平运动[11-12]。转座和大臂之间设置一个氮气弹簧结构，采用氮气弹簧辅助J2关节驱动，一方面可以减小J2关节伺服电机和减速机的负载，降低选型成本；另一方面氮气弹簧线性的阻尼效果，使关节运行更平稳。

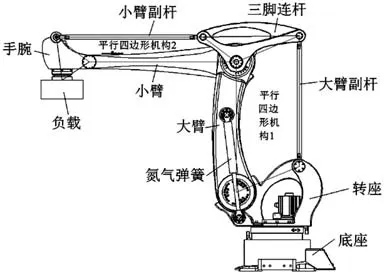
图1 GR4180码垛机器人结构Fig.1 Structure diagram of GR4180 palletizing robot

GR4180码垛机器人有4个旋转自由度，分别是转座绕底座的旋转（J1关节转动）、大臂的前后摆动（J2关节转动）、小臂的上下摆动（J3关节转动）、手腕末端的旋转（J4关节转动）。前3个轴与第四轴电机型号选用5 500 W和2 000 W。额定转矩分别为35.02 N·m和9.55 N·m，瞬时最大转矩为105.05 N·m和28.65 N·m。J1、J2、J3和J4各个轴减速比分别为111.28、222、141和81。码垛机器人的具体性能参数如表1所示。

表1 码垛机器人性能参数Tab.1 Performance parameters of palletizing robot

2 码垛机器人运动学模型

本文采用工业机器人控制中应用广泛的D-H参数法建立机器人运动学模型[13]，为码垛机器人GR4180每一个关节建立的D-H坐标系如图2所示，D-H参数如表2所示。

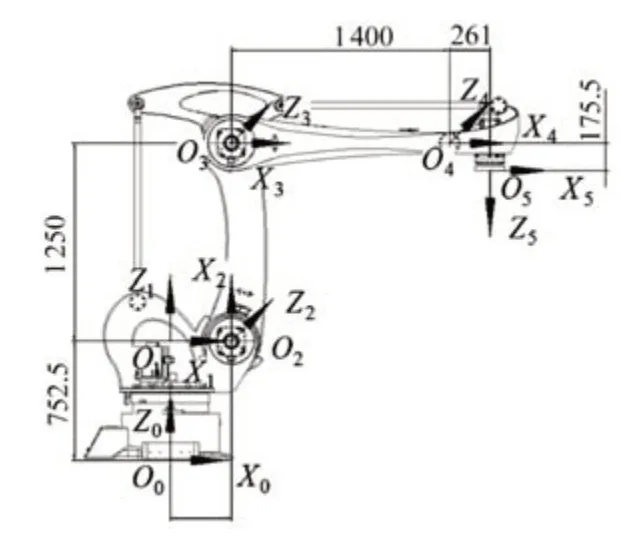
图2 GR4180码垛机器人D-H坐标系Fig.2 D-H coordinate system of GR4180 palletizing robot

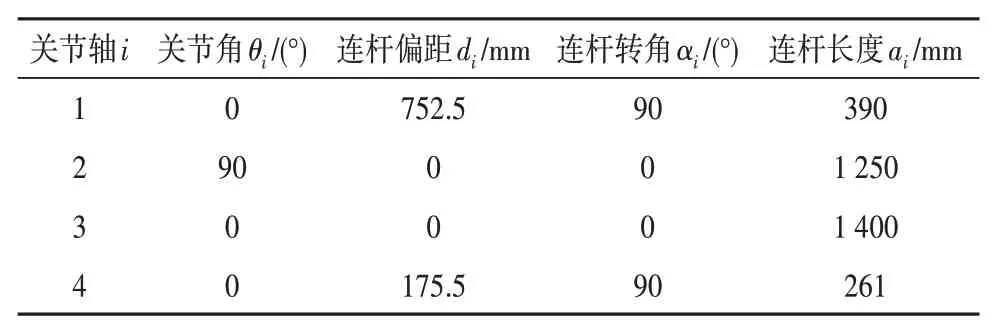
表2 码垛机器人D-H连杆参数Tab.2 D-H link parameters of palletizing robot

3 ADAMS动力学仿真分析

3.1 基于ADAMS的机器人仿真模型建立

可通过以下详细步骤建立ADAMS虚拟样机模型。

（1）将三维建模软件SolidWorks建立好的码垛机器人关键零部件进行简化重新装配，另存为Parasolid（.x_t）格式，导入ADAMS软件中[14]，如图3所示。

图3 码垛机器人虚拟样机模型Fig.3 Virtual prototype model of palletizing robot

（2）在SolidWorks软件中配置机器人所有零部件材料，测量机器人底座、转座、大臂、小臂、手腕、三角连杆、大臂副杆、小臂副杆、氮气弹簧上部、氮气弹簧下部和负载，各部分组件包含其内部所有零件的质量和转动惯量，将其动力学参数输入到ADAMS软件中。

（3）设置约束、驱动和载荷，底座与地面之间建立固定副，氮气弹簧上部和下部之间建立滑移副，其他位置相邻连杆之间建立旋转副。码垛机器人具有4个旋转自由度，需要在机器人旋转关节部位建立4个驱动。氮气弹簧之间建立一个单向力载荷，弹簧力函数：

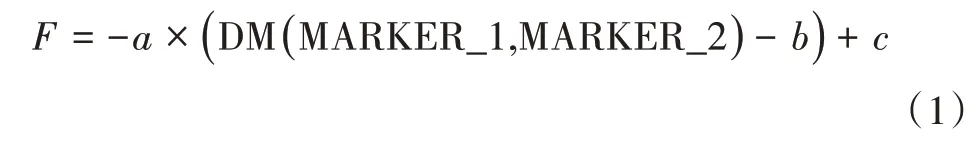
式中：常数a=35.3，b=989 mm，c=15 000 N，分别为氮气弹簧刚度系数、氮气弹簧初始长度和氮气弹簧初始力；MARKER_1和MARKER_2为氮气弹簧旋转轴作用点，DM（MARKER_1，MARKER_2）为氮气弹簧压缩后的距离，最后模型验证是成功的，可以进行动力学仿真分析。

3.2 动力学仿真分析

为了在实际工程中合理选型核心零部件电机和减速机，利用ADMAS软件进行仿真，获得机器人减速机所受转矩、关节角速度及角加速度。KEBA控制系统常用Sine square ramp加速度波形作为电机驱动函数，此函数优势使得机器人运动稳定，电机驱动转矩相对较低，实际工作时采用此加速度函数。根据机器人性能参数系统配置J1、J2、J3和J4各轴速度分别为120°/s、80°/s、120°/s和305°/s。系统配置加速度分别为216°/s2、240°/s2、530°/s2和2 220°/s2。

3.2.1 J1关节运动

在对机器人电机和减速机设计选型时，一般将机器人处于最大受力工况下进行校核，当机器人大臂和小臂同时处于与地面保持水平时，此处位置接近机器人最危险工况，但是实际上码垛机器人工作过程中极少或并不会应用此姿态进行工作。为避免过度浪费电机和减速机的性能，设置以下姿态进行仿真，机器人J2关节保持在30°，J3关节保持-30°，J4关节不动，满载满速进行回转运行。控制系统加速度驱动函数:

式中：at为加速度；am为系统配置最大加速度；t为变量时间；ta为加速时间，上式在0～ta时间段进行积分推出，ta=2vm/am；J1关节机器人最大速度为120°/s，加速度为216°/s2，加速时间ta=1.111 s，因此仿真分析加速度驱动函数为216d*SIN（PI*time/1.111）*SIN（PI*time/1.111）。电机与减速机转矩主要与加速度有关，在一个周期内加速度会经历0变化到最大最后再变为0，此时关节减速机转矩会产生最大值，所以设置仿真时间1.111 s，仿真步数Steps为500步，通过后处理得到机器人J1关节转矩、速度和加速度曲线，如图4所示。从曲线上可以看到加速时间1.11 s时，机器人加速到最大120°/s，在0.55 s时，机器人的加速度达到最大值为216°/s2，此时机器人关节产生最大的转矩为9 856.013 N·m。

图4 J1关节的角加速度、角速度和转矩曲线Fig.4 Angular acceleration，angular velocity and torque curves of J1 joint

将曲线数据提取出来，速度、加速度、转矩和时间一一对应整理到表格，计算公式如下:

式中：TM为电机输出转矩；TN为减速机负载转矩；i为减速比；η为传动效率；JM为电机转动惯量；α为角加速度。

获得电机的输出转矩值，将电机转矩值与转速绘制成为如图5曲线。此时可以看到电机转矩输出情况，电机转矩最大值为104.9 N·m，未超过J1电机转矩瞬时最大值105.05 N·m，此姿态运动下，机器人可以正常工作。

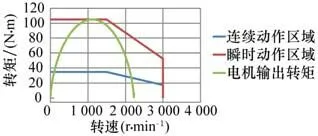
图5 J1关节电机输出转矩曲线Fig.5 Output torque curve of J1 joint motor

3.2.2 J2、J3关节联合运动

针对机器人抓取，码垛的过程，J2和J3关节联合加减速运动，设置以下姿态J1和J4轴保持不动，由于J2和J3关节之间存在氮气弹簧抵消一部分负载转矩，由力学分析当2轴旋转至65°时，氮气弹簧抵消后剩余的负载转矩最大，此时的情况最为负载受力最大工况，仿真模拟2轴初始角度65°，小臂始终保持与地面平行，为此设置J3加速度驱动函数与J2加速度保持一致方向相反为-240d*SIN（PI*time/0.666 7）*SIN（PI*time/0.666 7）。设置J2加速度驱动函数-240d*SIN（PI*time/0.666 7）*SIN（PI*time/0.666 7），设置仿真时间0.666 7 s，仿真步数Steps为500步，通过后处理得到机器人J2关节转矩、速度和加速度曲线，如图6所示。

图6 J2关节的角加速度、角速度和转矩曲线Fig.6 Angular acceleration，angular velocity and torque curves of J2 joint

从曲线上可以看到加速时间0.66 s时，机器人2轴加速到最大80°/s，在0.33 s时，机器人的加速度达到最大值为240°/s2，此时机器人关节产生最大的转矩为14 369.86 N·m。

根据上式（3）得到电机的输出转矩值，绘制成为如图7所示曲线，此时可以看到电机转矩输出情况，电机输出转矩曲线未超出电机转矩特性曲线的连续动作区域，电机可满足正常使用要求。

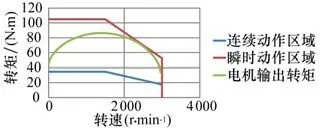
图7 J2关节电机输出转矩曲线Fig.7 Output torque curve of J2 joint motor

3.2.3 J3关节单独运动

J1、J2和J4关节保持不动，J3关节设置加速度驱动函数530d*SIN（PI*time/0.452 83）*SIN（PI*time/0.452 83），设置仿真时间0.452 83，steps为500步，通过后处理得到机器人J3关节转矩、速度和加速度曲线，如图8所示。

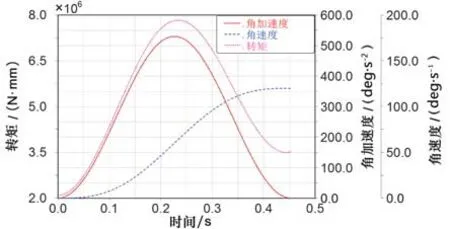
图8 J3关节的角加速度、角速度和转矩曲线Fig.8 Angular acceleration，angular velocity and torque curves of J3 joint

从曲线上可以看到加速时间0.452 8 s时，机器人3轴加速到最大120°/s，在0.233 7 s时，机器人的加速度达到最大值为529°/s2，此时机器人关节产生最大的转矩为7 832.977 N·m。

利用式（3）得到电机的输出转矩值，绘制成为如图9所示曲线。此时可以看到电机转矩输出曲线较电机转矩特性曲线连续动作区域还有一定距离，电机输出最大转矩未超过电机的瞬时最大转矩，电机满足正常使用情况。

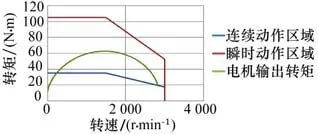
图9 J3关节电机输出转矩曲线Fig.9 Output torque curve of J3 joint motor

3.2.4 J4关节运动

J1，J2，J3关节保持不动，J4关节设置加速度驱动函数2220d*SIN（PI*time/0.2748）*SIN（PI*time/0.2748），设置仿真时间0.2748 s，steps为500步。通过后处理得到机器人J4关节转矩、速度和加速度曲线，如下图10所示。

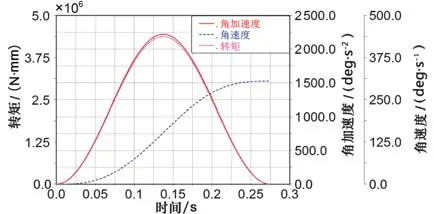
图10 J4关节的角加速度、角速度和转矩曲线Fig.10 Angular acceleration，angular velocity and torque curves of J4 joint

从曲线上可以看到加速时间在0.274 8 s时，J4关节速度为305°/s，在0.137 4 s时，机器人的加速度达到最大值为2 220°/s2，此时机器人关节产生最大的转矩为436.892 N·m。

利用公式（3）得到电机的输出转矩值，绘制成为如图11所示曲线。此时可以看到电机转矩输出情况远远小于电机的瞬时转矩，电机性能还有较多的余量未能发挥出来，此原因是为了防止机器人末端加速度过大而发生抖动，影响机器人的控制精度，所以设置了相对较低的J4关节加速度。

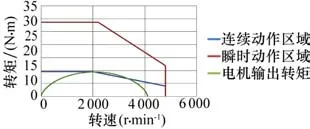
图11 J4关节电机输出转矩曲线Fig.11 Output torque curve of J4 joint motor

4 仿真与试验测试对比分析

为了验证所建立的虚拟样机模型仿真模拟得到的机器人关节所受转矩的合理性和精确性，搭建了码垛机器人GR4180的测试平台如图12所示，包括机器人本体，电控柜，数据监测装置等。通过示教器编程，码垛机器人运行姿态与上述仿真工况的姿态保持一致，利用驱动器监测软件进行电机电流数据采集与对比分析。机器人测试数据如图13～16所示。

图12 GR4180测试平台Fig.12 GR4180 test platform

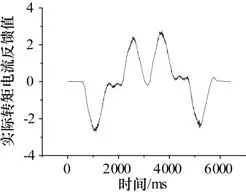
图13 J1电机测试数据Fig.13 Test data of J1 motor

图13为J1电机测试数据，此时运行姿态为J2关节保持在30°，J3关节保持在-30°，4轴始终保持不动，1轴运行角度为±90°，满载满速进行回转运行。从图中可以看到实际转矩电流反馈值绝对值最大为2.773 1，电机额定转矩35.02 N·m，电机实际输出转矩为97.11 N·m。图14所示为J2电机测试数据，此时J2和J3关节联合加减速运动，1轴和4轴始终保持不动，小臂始终与地面保持平行，J2关节运行角度-15°～60°满载满速进行伸缩运动。从图中可以看到实际转矩电流反馈值绝对值最大为2.354，电机实际输出转矩为82.44 N·m。图15为J3电机测试数据，J3关节单独运动，满载满速运行角度-15°～60°，其余关节轴保持不动。从图中可以看到实际转矩电流反馈值绝对值最大为1.999 7，电机实际输出转矩为70.03 N·m。图16为J4电机测试数据，机器人手腕轴满载满速下运行，角度范围±100°，其余关节不动。从图中可以看到实际转矩电流反馈值绝对值最大为0.957 3，电机额定转矩9.55 N·m，电机实际输出转矩为9.14 N·m。

图14 J2电机测试数据Fig.14 Test data of J2 motor

图15 J3电机测试数据Fig.15 Test data of J3 motor

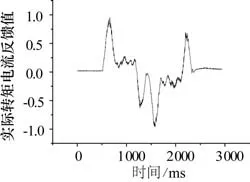
图16 J4电机测试数据Fig.16 Test data of J4 motor

将虚拟样机仿真模拟的电机输出转矩与试验测试数据对比分析，从图5、图7、图9、图11的各关节转矩输出曲线，读取到J1～J4各关节电机输出转矩分别为104.905 N·m，86.4744 N·m，62.81 N·m和9.4445 N·m。所以J1、J2、J3和J4电机的输出转矩误差分别为（104.905-2.773 1×35.02）÷（2.773 1×35.02）×100%=8%，（86.474 4-2.354×35.02）÷（2.354×35.02）×100%=4.9%，（62.81-1.999 7×35.02）÷（1.999 7×35.02）×100%=10.3%，（9.4445-0.957 3×9.55）÷（0.957 3×9.55）×100%=3.3%，J2电机转矩误差最大，为10.3%，其余均在10%以内，此方法建立的虚拟样机仿真模拟电机输出转矩与试验数据之间具有一定的可靠性，可用于码垛机器人设计和制造时前期的理论分析。

5 结束语

在码垛机器人的结构设计过程中，将SolidWorks软件建立的码垛机器人实体模型，导入到动力学仿真软件Adams中，建立了码垛机器人的虚拟样机模型，在前述4种工况下，仿真模拟了码垛机器人各关节负载转矩，角速度和角加速度，将数据处理获得了电机输出转矩。通过试验测试与仿真结果对比分析，在4种不同机器人的运行工况下，J1电机转矩误差为8%，J2电机转矩误差为4.9%，J3电机转矩误差为10.3%，J4电机转矩误差3.3%，证明所建立的虚拟样机模型动力学仿真具有较高的准确性。此方法可用于实际设计和生产中，缩短开发周期节约成本，对于码垛机器人的理论分析具有重要的指导意义。