微型钻头螺旋槽磨削机床精度标定方法的研究*

2022-08-26 07:58胡永祥徐魏斌付连宇杨晓钧

机电工程技术 2022年7期

胡永祥，徐魏斌，付连宇，杨晓钧※

（1.哈尔滨工业大学（深圳）机电工程与自动化学院，广东深圳 518000；2.深圳市金洲精工科技股份有限公司，广东深圳 518116）

0 引言

随着我国电子工业的飞速发展，作为元器件载体的PCB板的市场规模持续扩大。PCB板微孔加工通常采用机械钻孔的方式。为了提高刚度，微型钻头的螺旋槽常设计为变螺旋角形状。微型钻头加工最重要的工序为磨尖磨槽。机床的空间误差是影响微型钻头加工精度的重要因素，精度标定是解决这一问题的有效办法。精度标定主要包括机床空间误差建模、误差测量与辨识以及误差补偿3个部分。

对于机床误差建模，主要包括单项几何误差元素建模和机床空间几何误差建模。其中单项几何元素建模方法有切比雪夫多项式[1]、最小二乘法[2]等等，然而这些方法受制于多项式次数的选择，精度不够。为了提高拟合精度和速度，出现了基于神经网络[3]、人工鱼群算法[4]等新型建模方法。对于机床空间误差几何建模，传统建模方法建立多个坐标系，建模过程繁琐，基于旋量理论[5]和坐标系微分运动关系[6]等等的新型建模方法被大量研究应用。对于误差测量与辨识，根据测量方法有直接测量和间接测量。直接测量通常用激光干涉仪，但测量时间长，效率低。间接测量方法目前被广泛研究，主要有六圈法[6]、九线法[7]、体对角线分布测量法[8-9]等。对于机床误差补偿，传统补偿方法将空间误差模型的位置偏差量取反，但会产生较大的补偿残差，影响工件加工质量。重建工件CAD模型[10]的补偿方法于在线测量误差补偿中已普遍使用。基于迭代和递归[11]、粒子群[6]或者和遗传算法[12]等智能算法优化加工代码的方法，建模简单，补偿效果好。

本文首先设计了一款磨削加工微型钻头螺旋槽的专用机床，基于多体系统运动学和齐次坐标变换理论建立了磨削机床的空间误差模型。其次使用激光跟踪测量辨识出了机床的23项几何误差，得到了运动空间特征点的空间误差，之后基于BP神经网络训练拟合了这些误差数据，同时可以精确预测非特征点的空间误差。最后针对传统误差补偿方法的缺陷，提出了一种基于遗传算法优化加工代码的方法，降低了补偿后的残差，验证了算法的可行性。

1 微型钻头磨削机床的空间误差模型

图1所示为微型钻头磨削机床三维结构模型示意图，磨削机床结构主要由刀具链和工件链构成，其中刀具链由平动轴和手动转动轴组成，设定手动旋转轴将只影响砂轮的偏置角度，对砂轮刀具刀位点位置不造成影响，工件链由平动轴以及转动轴组成，在两条运动链路运动的组合下可实现微型钻头螺旋槽的磨削加工。

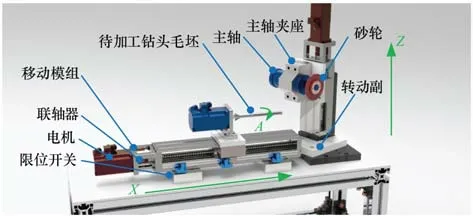
图1 微型钻头磨削机床三维结构模型示意图

图2所示为磨削机床机构示意图，其中构件0为机床床身，构件1为绕Z轴手动旋转轴，构件2包括了移动轴Z、砂轮主轴以及砂轮，构件3为移动轴X，构件4为旋转轴A以及相关构件。

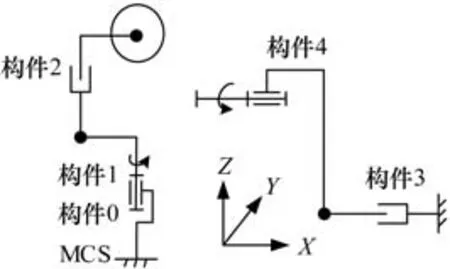
图2 微型钻头磨削机床机构示意图

在磨削机床上建立各坐标系如图3所示。将刀具链定义为第一运动链。在构件1手动旋转副轴线与机床床身交点处建立机床坐标系M CS/{1-1}。在移动轴Z的丝杠副运动中心轴线与手动旋转副平面的交点上建立运动坐标系{1-2}。在砂轮刀位点处建立刀具坐标系T C S/{1-3}。将工件链定义为第二运动链。在移动轴X的丝杠副运动中心轴线与机床床身交点处建立工件链初始坐标系{2-1}。在夹持微钻毛坯的旋转轴A中心轴线末端处建立运动坐标系{2-2}。在坐标系{2-2}处建立随旋转轴A旋转的工件坐标系WC S/{2-3}。

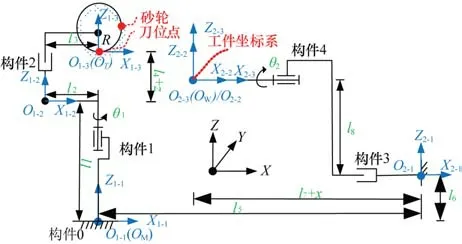
图3 机床坐标系建立

其中常量l1、l2分别为MC S与运动坐标系{1-2}的Z、X向偏距。常量l3、l4分别为运动坐标系{1-2}与TC S的X、Z向偏距。常量l5、l6分别为坐标系{2-1}与M C S的X、Z向偏距。常量l7、l8分别为运动坐标系{2-2}与坐标系{2-1}的X、Z向偏距。常量R为砂轮的半径。变量x、z分别为移动轴X、Z在参考坐标系下的运动量。变量θ1为砂轮偏置角度，微钻加工时为固定值。变量θ2为旋转轴A在参考坐标系下的运动量。

TC S相对于W C S的理想齐次变换矩阵为：

考虑磨削机床结构，会有23项几何误差对运动定位精度有影响，各轴几何误差如表1所示。

表1 机床几何误差元素表

结合机床的23项误差元素，此时磨削机床各运动轴之间的实际齐次坐标变换为：

T CS相对于W CS的实际齐次变换矩阵为：

磨削机床的综合空间误差模型则为：

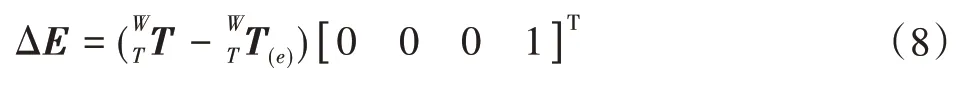
2 磨削机床误差测量与辨识

2.1 磨削机床平动轴与旋转轴的几何误差测量

本节利用激光跟踪仪测量辨识各轴的几何误差。激光跟踪仪是一种基于球坐标的测量仪器，其可以用来绘制自由曲面、跟踪物体的轨迹、测量零件的形位公差等等，因其测量结果精度高、测量范围大、操作简单的特点，广泛用于工业检测领域。

平动轴辨识基本原理为测量参考坐标系下参考点理论值与实际值之间的差值，差值又可以用机床各轴基本几何误差线性表示，从而能够解耦辨识出机床的各轴几何误差元素。如图4所示，在X轴参考坐标系O-xyz下，运动坐标系O x-x x y y z z初始坐标为(x0,y0,z0)，A1为激光跟踪仪靶球安放的位置，初始坐标为(x1,y1,z1)。

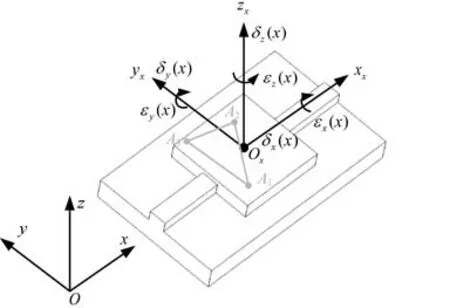
图4 平动轴几何误差辨识

理想情况下不考虑任何误差，移动平台运动量为x时，A1在参考坐标系下的坐标(x A1,y A1,z A1)为：

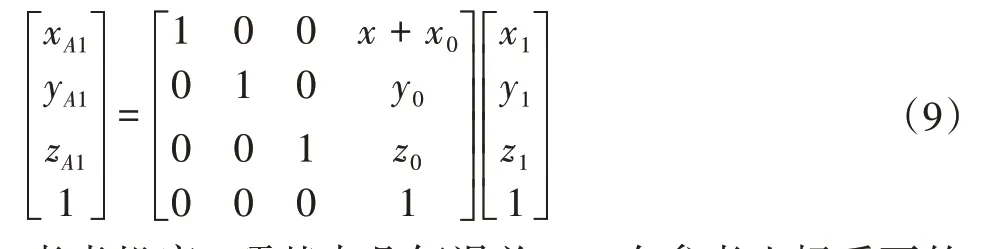
考虑机床6项基本几何误差，A1在参考坐标系下的坐标(x′A1,y′A1,z′A1)为：因此在X轴运动量为x时，A1的空间误差为：

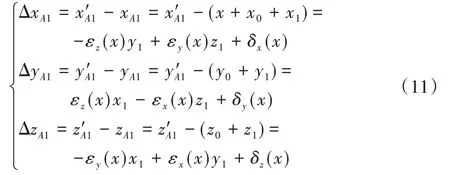
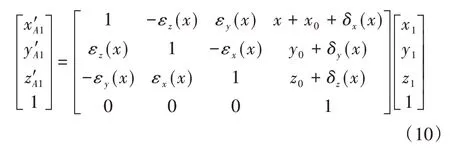
激光跟踪仪可以测量靶球A1点在参考坐标系下的实际坐标(x′A1,y′A1,z′A1)，为已知值。对于靶球A2、A3也类似，参考坐标系下A2、A3初始坐标分别为(x2,y2,z2)、(x3,y3,z3)，激光跟踪仪测得在参考坐标系下的实际坐标分别为(x′A2,y′A2,z′A2)、(x′A3,y′A3,z′A3)，联立A1、A2、A3的误差方程，将它们用矩阵形式进行表示如下：

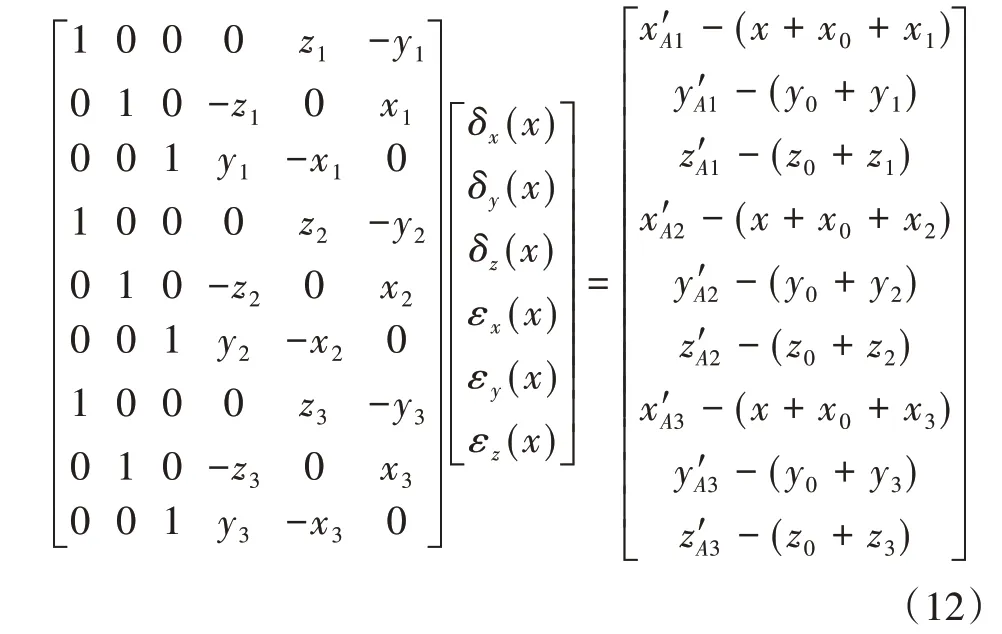
因为A1、A2、A3并不在同一条直线上，所以系数矩阵的秩为6，此时的方程具有唯一解。因此已知A1、A2、A3初始坐标，机床运动量为x，可以辨识当前机床移动轴X的6项基本几何误差。移动轴Z的辨识方法与X轴一致，不再赘述。

对于旋转轴A辨识方法也类似，如图5所示，在参考坐标系下，运动坐标系O A-x A y A z A初始坐标为(x′0,y′0,z′0)，激光跟踪仪靶球B1、B2、B3初始坐标为(x′1,y′1,z′1)、(x′2,y′2,z′2)、(x′3,y′3,z′3)，轴A运动量为θ，激光跟踪仪测得靶球B1、B2、B3实际随运动量θ变换的坐标为(x′B1,y′B1,z′B1)、(x′B2,y′B2,z′B2)、(x′B3,y′B3,z′B3)。其几何误差辨识矩阵方程为：

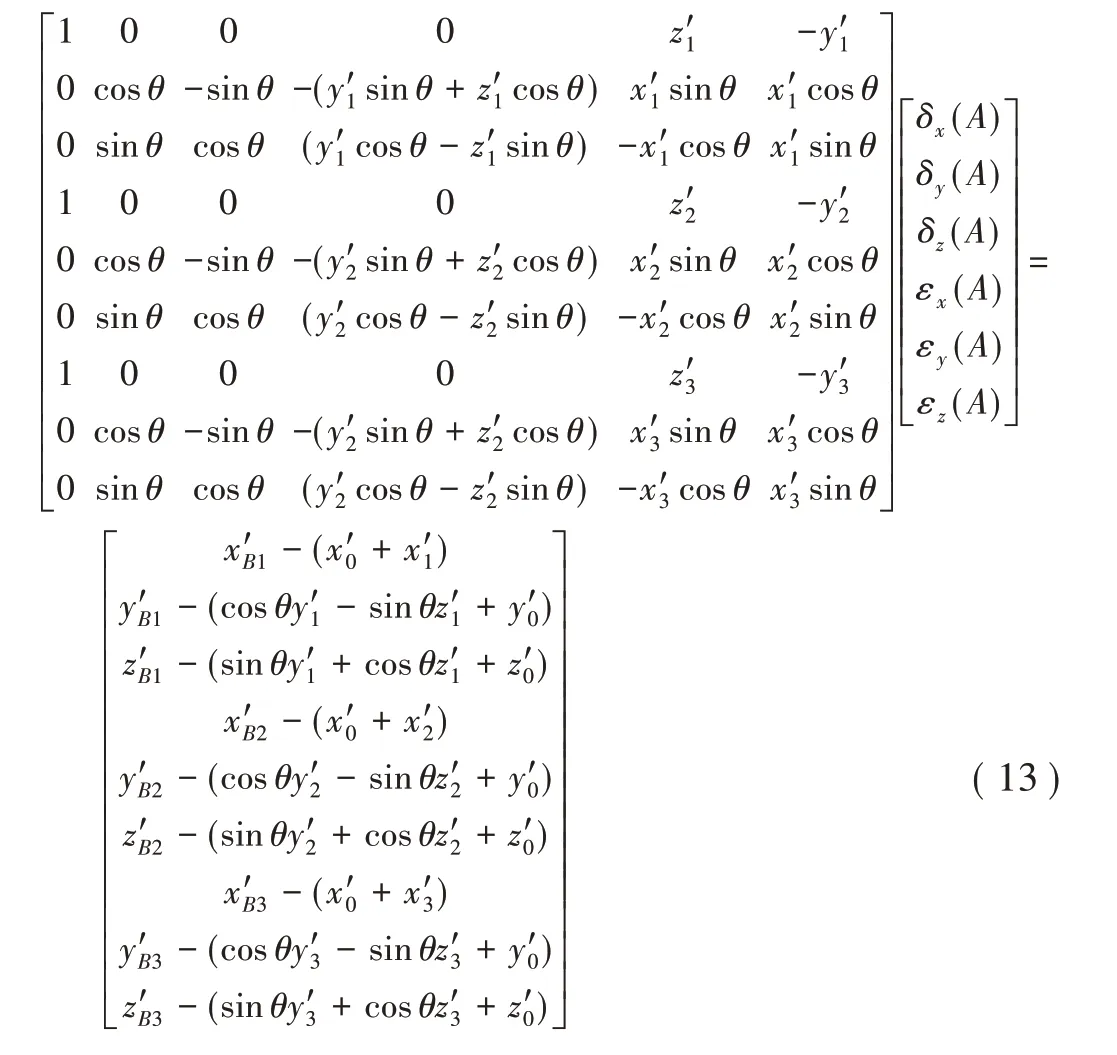
图5 旋转轴A几何误差辨识

同理B1、B2、B3并不在同一条直线上，所以系数矩阵的秩为6，此时方程组也一定具有唯一解。因此已知B1、B2、B3初始坐标，当运动量为θ时，可以辨识此运动量下旋转轴A的6项几何误差。

对于垂直度误差测量，如图6所示。将激光跟踪仪靶镜分别安装在X轴以及Z轴上，测量出一系列的点C1、C2、C3…Cn以及点D1、D2、D3…Dn，通过最小二乘法拟合直线，得到两条直线的方向向量，再通过数学运算计算两直线的角度大小，从而可以得到两平动轴垂直度S x z的大小。

图6 垂直度误差测量

对于旋转轴A本身轴线的两项线性误差和角度误差测量的方法，理论上旋转轴A初始状态时6项基本几何误差全部都为零，由于轴线存在4项几何误差，故实际辨识出来不为零的4项几何误差即为轴线的δy O A、δzO A、εyOA、εzOA。

平动轴X、Z与旋转轴A的几何误差辨识实验步骤都类似，测试系统安装如图7所示，实验步骤如下。

图7 基本几何误差辨识实验示意图

（1）将3个1.5 in的靶球固定在运动平台上，3个靶球安装形成三角形。固定激光跟踪仪。电机驱动各轴平台移动，每隔运动行程的1/20停止并测量3靶球在激光跟踪仪下的位置，共测量21组。

（2）对于平动轴X，利用最小二乘法直线拟合每组三角形的重心位置，将拟合的直线视作为参考坐标系的X轴，选择过靶球A1初始位置同时与X轴垂直的直线作为参考坐标系的Y轴；移动轴Z类似，不再展开。对于旋转轴A，利用最小二乘法拟合每个靶球的回转轴线，取三靶球的平均回转轴线作为参考坐标系的X轴，选择过靶球B1初始位置同时与X轴垂直的直线作为参考坐标系的Y轴。

（3）计算参考坐标系与激光跟踪仪坐标系之间的转换关系，把在激光跟踪仪坐标系下测量的靶球位置转换成参考坐标系下的位置。建立运动坐标系，其方向与参考坐标系方向相同，起始位置也一样。确定3个靶球在参考坐标系下的起始位置。

（4）运用式（12）或式（13）中提出的平动轴和旋转轴几何误差辨识矩阵，得到各运动轴各个运动位置的6项基本几何误差，并通过B样条对数据进行拟合。最终各轴基本几何误差辨识结果如图8所示。

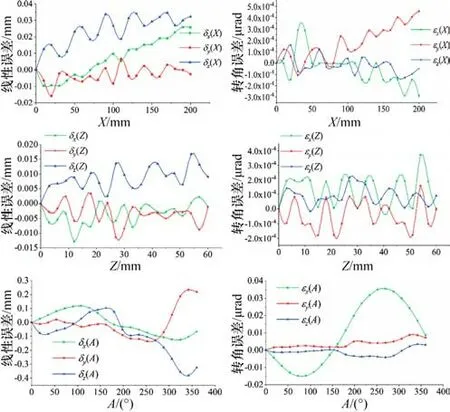
图8 各轴几何误差辨识结果

另外对于X、Z轴平动轴的垂直度误差测量，实验平台安装如图9所示，具体实验步骤如下：

图9 垂直度误差辨识实验示意图

（1）固定激光跟踪仪。将两靶球分别安装至X、Z轴移动平台上，电机驱动平台移动，测量其运动轨迹，即连续分别测量n1、n2组数据。

（2）利用最小二乘法分别直线拟合X、Z轴的n1、n2组数据，得到X、Z轴的方向向量，从而求得X、Z轴之间的垂直度误差。

根据最小二乘法的拟合结果，在激光跟踪仪坐标系下的X轴的方向向量为（-0.950 1，-0.311 8，-6.609 4×10-4），Z轴的方向向量为（0.007 7，-0.021 4，-0.999 7），所以垂直度误差为S xz=2.5668×10-2μrad。

针对旋转轴A轴线的两项线性误差以及两项角度误差，通过辨识旋转轴初始状态即可从旋转轴几何误差矩阵获得4项几何误差的数值大小，最后辨识结果为δyO A=-5.673 2μm、δzOA=-5.238 9μm、εyOA=1.326 1μm、εzOA=-0.782 1μm。

2.2 基于BP神经网络的空间误差拟合

通过激光跟踪仪测量辨识出机床工作空间的各项几何误差之后，将这些几何误差元素代入空间误差模型中，可以得到整个运动工作空间的空间误差。这些空间误差为离散值，需要进行拟合。目前有将各轴单项基本几何误差数据运行多项式回归或者最小二乘法等方法进行拟合，最后将这些数学表达式代入空间误差模型中的方法。然而这种方法需要为每个基本几何误差项数据拟合，操作繁琐；第二，精度无法达到要求，特征点误差较大，非特征点预估数据更加无法预估。由于整个机床运动空间的特征点数据杂乱无序，本章采用BP神经网络对这些特征点的空间误差数据进行拟合，旨在精确拟合各特征点数据，为非特征点数据提供高精度的预估值。

移动轴X的运动行程为200 mm，移动轴Z移动行程为60 mm，旋转轴A运动行程为360°。首先将磨削机床的运动空间三坐标轴进行10等份，从而得到11×11×11个特征点运动空间坐标值，如图10所示，将坐标值当作BP神经网络的输入样本，即(x,z,θ)，输出样本为运动空间的特征点空间误差值(Δx,Δy,Δz)。训练完毕之后，机床运动任意运动空间位置都可通过BP神经网络得到空间误差值。

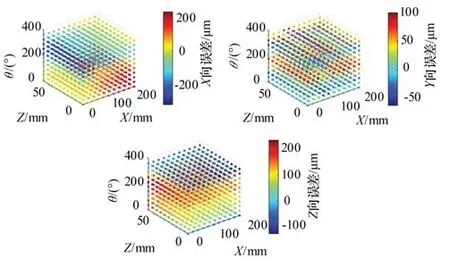
图10 BP神经网络输入样本和输出样本

根据训练集的数据特点，Δ输出层和输出层神经元数设置为3。BP神经网络整体结构如图11所示。

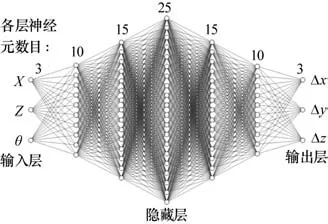
图11 BP神经网络结构

整个BP神经网络共7层，隐含层层含有的神经元数为10、15、25、15、10。设置均方误差为2.5×10-10μm，学习速率为0.05，激活函数全部采用sigmoid，最大训练次数为100 000，训练方法为LM梯度下降法训练。

2.3 空间误差数据神经网络拟合分析

如图12所示，将特征点的原始空间误差数据与BP神经网络拟合空间误差误差数据对比，当最大拟合误差为0.026 7μm时，原始空间误差为343.502 5μm，BP神经网络拟合空间误差为343.522 5μm，误差率为7.772 9×10-5，BP神经网络特征点拟合准确率达99.99%。

图12 原始误差与神经网络拟合空间误差对比

为了更清楚地分析BP神经网络的拟合情况，考虑旋转轴θ=0时，取X、Z两平动轴的运动空间，如图13所示，X、Y、Z向拟合误差分别保持在[-9.495 5×10-3μm，7.409 0×10-3μm]、[-2.444 9×10-3μm，3.198 7×10-3μm]、[-5.693 1×10-3μm，4.033 2×10-3μm]，说明神经网络拟合效果确实比较好，精度高。

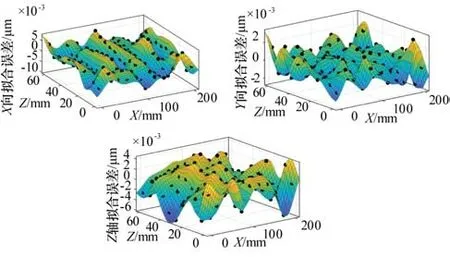
图13 BP神经网络拟合机床误差

3 磨削机床空间误差补偿

3.1 基于遗传算法的加工代码优化

前文已经完成了误差建模与误差测量和辨识，而这些工作主要是为误差补偿而服务。误差补偿，即在实际加工中补偿误差，减少机床误差对加工工件的影响，提高工件的加工精度。目前普遍采用的传统补偿方法基本思想是在已知加工点空间误差大小和方向的情况下，反向施加同等大小方向相反的空间误差，这样实际加工位置点会更接近理想加工位置点，从而提高了加工精度。

然而，传统补偿方法在原理上依旧有不足之处，实际加工结果误差较大。原因在于，机床空间误差是与实际加工位置有关的物理量或者说与各运动轴实际的运动量有关。如图14所示，传统补偿方法中，理想加工位置Pd的空间误差为Ed，反向施加一个大小相等的误差后的目标优化位置Pr的空间误差Er并不等于Ed，实际加工过程中，每一个插补点都会产生或大或小的残差。

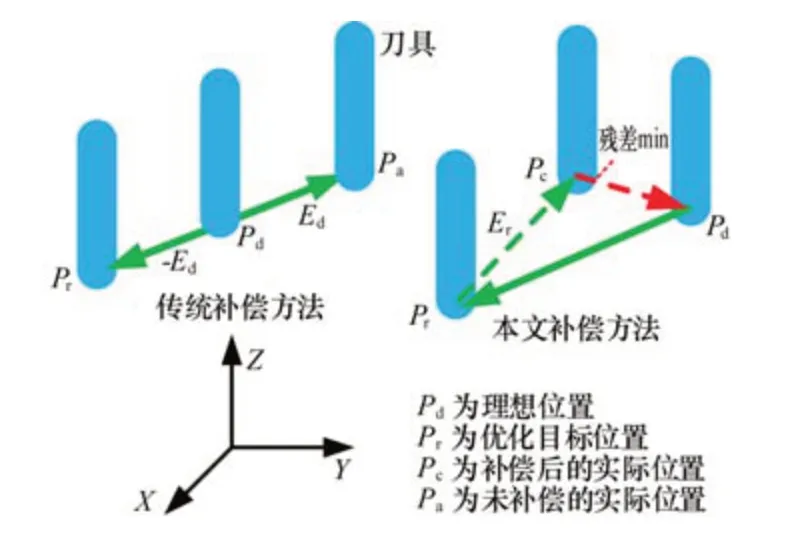
图14 传统补偿与本文补偿方法比较

本节将误差补偿问题转换为最优化设计问题。主要以残差为优化指标，力求在整个加工过程中使得残差最小。建立目标优化函数如下:

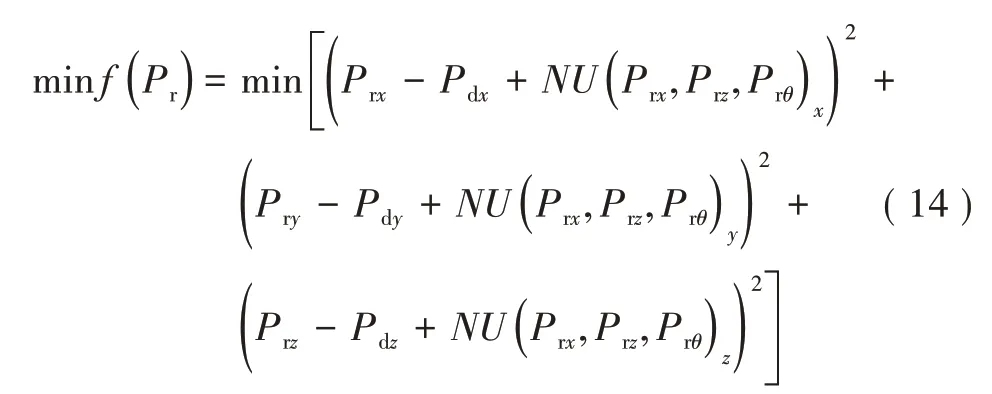
式中：(Pdx,Pdz,Pdz)为理想加工位置点，已知量。(Prx,Prz,Prz)为目标优化位置点，目标优化量。(P rx,P rz,P rθ)为目标优化位置点后置处理得到的各轴运动量。NU(Prx,Prz,Prθ)x、N U(Prx,Prz,Prθ)y、NU(Prx,Prz,Prθ)z分别为当各轴运动量为(Prx,Prz,Prθ)时BP网络输出的x、y、z向误差。

另外通过第2章的分析可知，机床各向误差数据最大值不超过250μm，因此目标优化位置点各分量约束条件为：

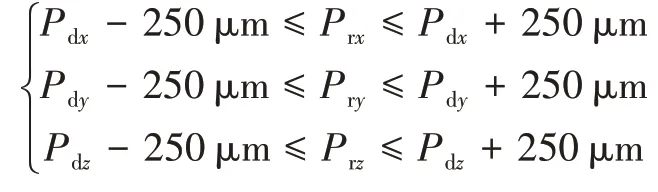
如图15所示，整个目标优化位置点的搜索区域为以理想加工位置Pd为中心的直径250μm的球形区域。由于每个目标位置的分量都小于极限分量250μm，所以一定存在最优解。

图15 目标优化位置点的搜索区域

可以看到此时的目标位置优化问题实际上是一个多约束的非线性规划问题，本章采用遗传算法进行最优值求解，求解流程如图16所示。遗传算法初始条件设置为：种群大小40，最大遗传代数400，变量维数3，选择概率0.7，交叉概率0.7，变异概率0.2。

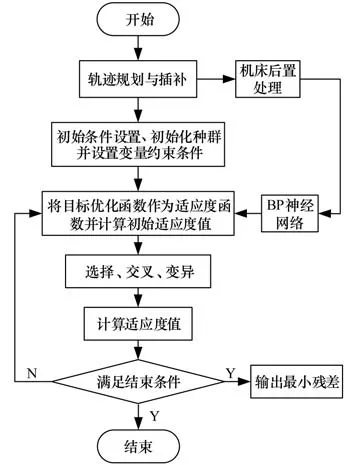
图16 遗传算法求解最小残差流程

3.2 微型钻头误差补偿优化结果

运用本文误差补偿算法和传统补偿方法至图17中需加工的微型钻头变螺旋角槽线加工轨迹中。

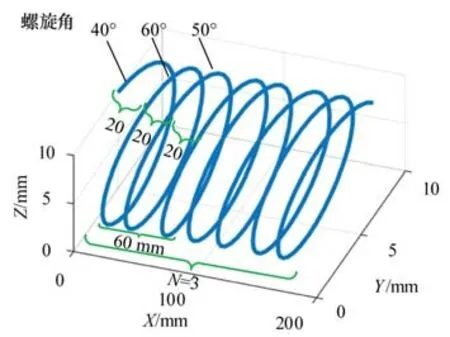
图17 变螺旋角加工路径

运行结果如图18所示。首先解释一下传统补偿方法残差呈现类似周期性的原因。由第二章辨识结果可知机床空间误差受到旋转轴的影响最大，旋转轴A的6项基本几何误差在一圈内呈现近似正弦函数变化，且会出现一次最小值和最大值，故此传统补偿残差在一圈内同样会出现最小值和最大值，同时残差呈现类似正弦函数的轨迹。由于本次补偿的加工轨迹共7圈，所以总共7次相似的残差轮廓。其次，从图18中可知本章提出的算法将传统补偿的残差平方最大值160.058 5μm降至0.070 48μm，残差平方平均值45.847 6μm降至0.000 3μm，且所有插补点中残差远远小于传统补偿的残差。由此说明对于微型钻头加工而言，本文提出的补偿方法能十分有效地提高加工精度，同时也验证了算法的可行性。

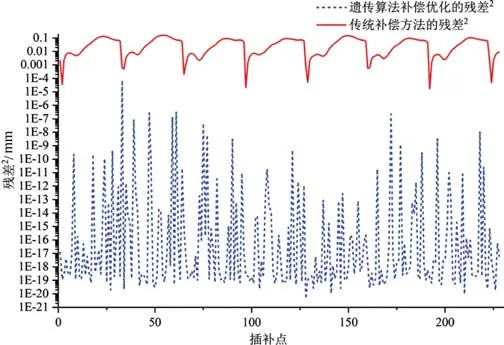
图18 变螺旋角加工路径误差补偿结果

4 结束语

（1）针对微型钻头磨削机床的结构特点，分析了机床的几何误差元素，并根据齐次坐标变换和多体系统运动学建立了磨削机床综合空间误差模型。

（2）确立了基于激光跟踪仪的平动轴和旋转轴几何误差测量与辨识方法，测量解耦出了机床的23项结合误差，并运用7层的BP神经网络对空间误差特征点数据进行拟合，同时精确预测非特征点的空间误差，拟合准确率高达99.99%。

（3）针对于传统补偿方法的缺陷，将误差补偿问题转换为最优化设计问题，并基于遗传算法优化加工轨迹，减小补偿残差对加工的影响。最终，将插补点传统补偿残差平方的最大值由160.058 5μm降至0.070 48μm，平均值由45.847 6μm降至0.000 3μm，补偿效果显著有效。