基于A*蚁群融合算法的避障路径规划研究*

绳红强，黄海英，崔毅刚

（1.中国重汽集团济南动力有限公司，济南 250101；2.武汉大学数学与统计学院，武汉 430072；3.山东圣翰财贸职业学院，济南 250316）

0 引言

智能车辆是一个集环境感知、规划决策和轨迹跟踪控制等功能于一体的综合系统。随着新一代人工智能技术的快速发展，智能车辆已成为未来汽车产业的重要发展方向。避障路径规划是智能车辆领域的关键技术之一，是当前国内外学者研究的热点[1-5]。

智能车辆避障路径规划一般是指在障碍物环境中，满足路径平滑度最高、距离最短、能耗最小等约束条件下，从车辆起始点到目标点规划出一条无碰撞路径。路径规划算法主要有人工场势法[6]、概率路图法（PRM）[7]、快速随机拓展树法（RRT）[8]、几何曲线插值法[9]、D*算法[10]、A*算法[11]、蚁群算法[12-16]、粒子群算法[17]等。智能车辆安全行驶对路径规划算法效率、路径平滑性提出了较高的要求，而每种路径规划算法适用领域不同，导致单算法结构不具有泛化求解能力，往往针对具体问题需要进行优化整合。蚁群算法是由意大利学者M Dorigo等[14]于1996年提出，它源于模拟蚁群觅食行为完成寻路过程，通过残留信息素计算路径节点选择概率，最终得到优化的规划路径。蚁群算法鲁棒性强，易于与其他优化算法相结合，实际应用中存在规划路径不光滑、路径曲折和收敛速度慢的问题[18-20]。

针对上述蚁群算法存在的缺陷，本文通过对蚁群算法启发函数和信息素更新策略改进，提出一种适用于智能车辆的基于A*蚁群融合算法的避障路径规划方法。该方法不仅融合A*算法估价值和转弯拐角约束条件，构造了一种增强型启发函数，还设计改进了信息素浓度增量模型。仿真结果表明，本文算法在改善规划路径平滑度和算法性能方面效果明显。

1 蚁群算法

由于蚁群算法原理在M Dorigo等人的著作已有详尽的描述，在此不做赘述。蚁群算法的核心是利用状态转移概率和信息素更新策略实现路径选择。

1.1 状态转移概率

迭代过程中，蚂蚁m（m=1，2，3，…，M）在t时刻从当前节点i转移到下一节点j的状态转移概率由路径上的信息素浓度和两点间的距离启发函数确定。状态转移概率表达式如下：

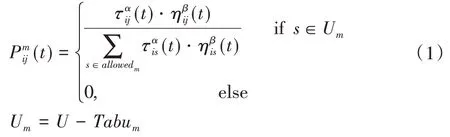
蚁群算法启发函数ηij(t)表达式为：

式中：di j为节点i和j之间的距离，即：

1.2 信息素更新策略

当所有蚂蚁完成一次迭代后，需对路径信息素进行更新，其更新公式为：

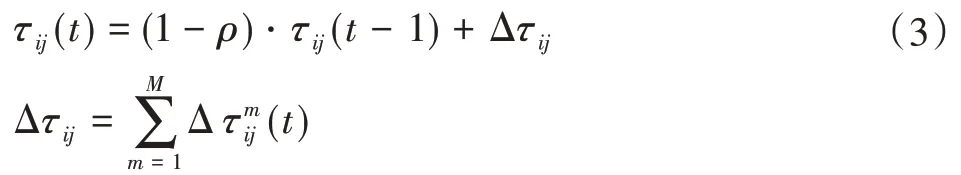
式中：τij(t)为t时刻节点i到下一节点j路径之间的信息素浓度；τij(t-1)为在t-1时刻节点i到下一节点j路径之间的信息素浓度；ρ为信息素挥发系数，ρ∈(0,1)；Δτij为M只蚂蚁完成一次迭代，边（i，j）上累积残留的信息素浓度；为第m只蚂蚁完成一次循环边（i，j）上残留的信息素浓度。

M Dorigo等人提出3种不同的信息素浓度增量模型，分别称之为Ant-Density System（ADS）、Ant-Quantity System（AQS）和Ant-Cycle System（ACS）模型。

若第m只蚂蚁当前循环经过边（i，j）的集合为，则 信息 素浓 度 增量模型函数表示如下。

ADS模型：

式中：Q为信息素强度，影响算法求解速度，为大于零的常数；Lm为第m只蚂蚁在本次循环中所经过路径的总长度。

上述ACS模型采用的是全局更新策略，蚂蚁完成一个循环后再更新残留信息素的浓度，在求解路径规划问题中最为常用，因此本文采用该模型作为信息素更新的基本模型。

2 改进蚁群算法

由于蚁群算法启发函数ηis(t)=1/d ij仅利用相邻节点的信息，全局启发性不足，易出现规划路径拐角多、盲目搜索和收敛速度慢问题。下面从启发函数和信息素更新策略两方面对算法进行改进。

2.1 构造基于A＊算法的启发函数

A*算法是一种启发式搜索算法，其核心是利用估价函数在状态空间中从起始点开始对每一个搜索位置进行评估，按照评价准则（如路径最短或消耗最小等指标）选取最优的位置，再从这个位置进行搜索直到目标位置。以最短路径作为搜索评价指标，A*算法估价函数的可表达式为：

式中：n为起始节点相邻的节点；F（n）为节点n的估价函数；G（n）为在状态空间中从初始节点s到节点n的最短距离；H（n）为从节点n到目标节点g的最短距离；nx为节点n的横坐标；ny为节点n的纵坐标；sx为起始节点的横坐标；sy为起始节点s的纵坐标；gx为目标节点的横坐标；gy为目标节点g的纵坐标。

引入A*算法估计代价F（n）和拐角惩罚函数f(θij)作为蚁群算法启发函数的启发因子，改进后的蚁群算法启发函数表达式如下：

式中：t为目标节点g影响路径选择的权重；θij为从节点i经过相邻节点j转过的角度；f(θij)为节点i与节点j之间的拐角惩罚函数；C为惩罚函数系数，为一常量。

2.2 改进信息素浓度增量模型

利用蚂蚁当前路径、最优路径和最差路径，以及将当前迭代路径累积拐角惩罚函数，优化信息素浓度增量模型。优化后的信息素浓度增量模型表达式如下：

式中：Q*为信息度浓度的强度值；n为当前迭代次数；Ln,m为当前路径长度，即第m只蚂蚁产生的路径的长度；Lmin为最优路径长度，即第n次迭代产生的最短路径长度；Lmax为最差路径长度，即第n次迭代产生的最长路径长度；为当前迭代最短路径上各点拐角的累积惩罚值；δ为路径偏离值，δ=Lmax-L n,m，即最差路径的长度与当前路径长度之间的差值；ε为第n次迭代路径允许误差。

在迭代过程中，新的信息素增量机制可以自适应动态调整信息素的强度，使优化过程加速向全局最优路径收敛。当δ＞ε时，Lmax与Ln,m差值越大，信息素强度越大，全局收敛时间缩短，算法求解效率得到提升；当δ≤ε时，L n,m与Lmin越接近，信息素浓度蒸发越快，使算法避免出现过早收敛陷入局部最优。引入，保证迭代过程中拐角最小路径上的信息素浓度得到加强，利于改善路径平滑性。

2.3 改进算法步骤

本文提出的基于A*蚁群融合算法的避障路径规划方法算法步骤如下。

（1）创建栅格地图环境。选择起始点和目标点。

（2）初始化参数：蚂蚁规模M，最大迭代次数N，信息启发式因子α，期望启发式因子β，信息素挥发系数ρ等。设定初始迭代次数n=1（n=1，2，3，…，N），初始蚂蚁编号m=1（m=1，2，3，…，M），并把起始点S置入禁忌表Tabu。

（3）路径选择。访问um查找当前节点前往下一步可行节点，按式（1）和（8）分别计算下一步可行节点的概率，然后，按轮盘法选择下一节点。将选定的下一节点作为新的起始点即当前节点，更新禁忌表Tabu。

（4）蚂蚁序号更新。若第m只蚂蚁的当前节点列表包含了目标点或无路径且m≥M，则转入步骤5；否则，m=m+1，返回步骤3。

（5）信息素更新。计算当前迭代最优路径并按式（3）和（9）更新信息素浓度。

（6）迭代或停止。若n≥N，则输出最优路径并停止迭代；否则，n=n+1，释放禁忌表Tab u，返回步骤3。

3 仿真分析

3.1 仿真环境地图模型

本文采用栅格法构建工作空间地图模型，栅格法是将智能车辆行驶的空间分解成N×N具有二值信息的网格单元。下面以10×10栅格地图为例，简要说明栅格地图模型表示方法，如图1所示。

图1 栅格地图

图1中黑色占有的栅格表示障碍物，白色占有的栅格是可行栅格。按从左到右，从上到下的顺序，依次为栅格进行编号，栅格中心的坐标为直角坐标，则栅格地图中的任意一点的坐标（xi，yi）与栅格编号i的映射关系如式（10）和式（11）所示：

式中：a为栅格边长；N×N为栅格编号数值最大的值；mod(a,b)为（a/b）取余结果；ceil函数为朝正无穷大方向取整。

被控对象在某一个栅格内可到达的栅格有与其相邻的上、右、下、左、右上、右下、左下、左上8个方向上的栅格，如图2所示。

图2 八个可行方向

3.2 仿真结果分析

为了验证改进蚁群算法的有效性，本文通过仿真程序，在3种复杂障碍物环境栅格地图（20×20）下，对基本蚁群算法和本文改进蚁群算法进行了仿真对比分析。仿真试验参数设置如表1所示。仿真结果如图3～5和表2所示。

表1 仿真实验参数设置

图3是在地图1环境下仿真结果，是基本蚁群算法和本文提出的改进蚁群融算法的避障路径规划图和迭代收敛曲线。如表2所示，本文改进蚁群算法较基本蚁群算法迭代收敛速率提高了54.55%，最优路径减少了38.04%，拐点数减少了57.69%，路径平滑度即拐角之和提高了78.85%。

图3 基于地图1环境下两种算法最短路径规划图和迭代收敛变化曲线

图4是在地图2环境下仿真结果，如表2所示，本文改进蚁群算法较基本蚁群算法迭代收敛速率提高了40%，最优路径减少了42.75%，拐点数减少了50%，路径平滑度即拐角之和提高了75%。

图4 基于地图2环境下两种算法最短路径规划图和迭代收敛变化曲线

图5是在地图3环境下仿真结果，如表2所示，本文改进蚁群算法较基本蚁群算法迭代收敛速率提高了45.41%，最优路径减少了38.49%，拐点数减少了44%，路径平滑度即拐角之和提高了72%。

图5 基于地图3环境下两种算法路径规划图和迭代收敛变化曲线

表2 仿真实验结果

综合上述3种地图环境下两种算法的仿真结果，本文改进的蚁群算法即A*蚁群融合算法较基本蚁群算法环境适应能力强，迭代收敛速率平均提高了41.67%，最优路径减少了39.76%，拐点数减少了50.56%，路径平滑度即拐角之和提高了75.28%。

4 结束语

基本蚁群算法在智能车辆避障路径规划中存在拐角多、收敛速度慢、泛化求解能力差等问题，本文通过对基本蚁群算法改进，提出一种基于A*蚁群融合算法的智能车辆避障路径规划方法，仿真结果显示改进效果良好。特别是在算法收敛速度、最优路径和路径平滑度等方面改进效果明显。引入A*算法估价因子和路径拐角惩罚因子，构造的增强型启发函数在引导蚂蚁对引导目标节点的感知、消除路径搜索的盲目性和提高路径平滑度方面作用明显；提出的基于拐角惩罚因子的自适应信息素浓度增量模型，可以动态调整信息素浓度的强度使算法快速向转角最小的最优路径收敛。