基于改进MKECA算法的注塑机异常检测*

黄梓伟，印四华

（广东工业大学机电工程学院，广州 510006）

0 引言

随着社会的进步和生产技术的发展，塑料和钢铁、混凝土、木材成为当今四大工业材料[1]。受益于人均塑料使用量的增长，世界塑料的总产量在2016—2018年呈现逐年增加的趋势，在2018年，中国塑料产量占比达到亚洲塑料产量的30%，高达1.08亿吨，高居亚洲第一[2]。综合来看，注塑行业占有庞大的市场，具有广阔的市场前景。

注塑成型过程属于典型的间歇过程，本身具有反应复杂、多工序、变量高度耦合等特点，由于工作环境恶劣以及以及设备老化等问题，注塑机实际工作中可能会出现各种异常，进而造成注塑零件质量缺陷以及能源浪费等问题[3]。企业通过现场定期巡查的方式检查注塑机是否异常，存在效率低下、人工成本高等问题。随着物联网技术的发展，注塑成型过程采集到的工业过程数据为基于数据驱动的注塑机异常检测方法提供了数据基础。

基于数据驱动的多元统计分析方法在间歇工业过程异常检测中得到了广泛的应用，如多向主成分分析（MPCA）[4-6]和多向偏最小二乘（MPLS）[7-8]通过对过程数据进行特征提取，并基于降维处理后的数据建立检测模型，但以上方法要求过程变量服从多元高斯分布以及线性关系，当过程变量不服从非高斯分布或呈现非线性关系时，势必提高系统的漏报率和误报率。

考虑到实际工业过程变量呈现强非线性，Jessen[9]在KPCA的基础上提出一种非线性特征提取算法——核熵成分分析（KECA），它是从瑞利熵损失最小的角度提取过程的非线性特征信息，在数据结构特征提取上具有一定的优势。KECA方法被引入间歇工业过程中，称为多向核熵成分分析（MKECA）[10-11]，但MKECA没有考虑到复杂工业过程具有的多模态和非高斯特性，异常检测性能有待提高。针对多模态问题，Ma[12]根据不同模态数据均值和标准差存在差异的特点，提出局部近邻标准化取代全局标准化策略对数据进行预处理，解决了复杂工业数据存在的多模态问题。顾幸生等[13]将LNS和MKECA相结合进行特征提取，但其忽略了数据的非高斯特性。

MKECA对降维后的数据建立T2和Q统计量进行异常检测，由于注塑成型过程数据存在混合分布的情况，检测效果受限[14]。Tax等[15]在支持向量机（SVM）的基础上提出了支持向量数据描述（SVDD）算法，该算法对数据的分布没有要求，可以应用于数据不服从多元高斯分布的情况下的异常检测[16-18]。

综上，本文针对注塑成型过程中存在多模态、混合分布等问题，对MKECA方法提出相应的改进。改进的MKECA方法首先对每个样本求取局部近邻集，根据局部近邻集的均值和标准差对样本进行标准化；然后采用MKECA算法进行特征提取，利用降维后的训练集对SVDD进行异常检测，通过对测试样本计算统计量D以判断注塑机是否异常。最终通过实验验证本方法的对注塑机异常检测的有效性和优越性。

1 问题描述

注塑机的大致结构如图1所示，其主要包括电气控制系统、液压传动系统、润滑系统、合模系统、加热及冷却系统、注射系统等部分组成。

图1 注塑机结构

注塑成型过程是一个典型的间歇生产过程：颗粒状的高分子材料进入机筒，经过螺杆的挤压和加热装置加热后成为熔融态。在螺杆的推动作用下，熔体通过机筒前端的喷嘴进入模具型腔，经过一段时间的冷却后成为塑料制品。

基于数据驱动的多元统计分析方法具有以下假设：各变量服从高斯分布、线性系统、单一模态等。工业过程往往是强非线性过程；由于外界环境变化以及生产计划的更改以及注塑机本身固有特性等因素，注塑成型过程具有多个稳定工况，需要频繁更换生产条件，导致其具有多模态的特性；此外，工业过程的数据往往存在混合分布的特点。

综上，传统多元统计分析方法要求数据满足某些假设，而如果忽略了注塑机本身存在的特性，简单采用传统的多元统计算法进行检测，必然很难对注塑成型过程进行有效地监控，造成异常检出率不高的后果。

2 基础算法

2.1 局部近邻标准化

由于工业过程变量的量纲存在差异，在进行数据分析之前往往需要全局标准化统一量纲：

式中：xi为原始数据集中的每个样本；mean(X)为所有样本的均值；s td(X)为所有样本的标准差；zi为经过标准化的样本。

经过z-score处理后的数据消除变量之间量纲不一致的影响，但不能将多模态数据统一为单一模态。多模态数据具有多中心、各工况分布结构不同的特点，故本文采用局部近邻标准化（LNS）[12]对方差显著不同的多模态数据进行预处理：首先根据欧氏距离计算出样本x i与其他样本的距离，并选取前k个近邻样本组成样本x i的近邻集；其次根据式（2）和式（3）计算出xi近邻集N(xi)的均值和标准差，然后根据式（4）进行局部近邻标准化处理：

式中：m(N(x i))为xi近邻集N(xi)的均值；s(N(x i))为xi近邻集N(xi)的标准差。

通过LNS操作将不同分布、不同中心的多模态数据聚合为离散程度和中心近似相同的单模态数据。

2.2 核熵成分分析

核熵成分分析（KECA）是一种非线性特征提取方法，由于其能够有效减小降维前后数据信息损失，改善模型性能，近年来被引入到工业过程检测领域[19-20]。

核熵成分分析（KECA）采用瑞利熵对数据信息进行度量，其表达形式为：

式中：H(p)为瑞利熵；p(x)为中心化后的样本x的概率密度函数。

由于对数函数的单调性，式（5）可以转化为：

通过对V(p)的估计可求得瑞利熵H(p)。p(x)通过parzen密度估计法进行估计：

将式（7）代入式（6），以均值对V(p)进行估计即可实现对H(p)的分析。因此可得：

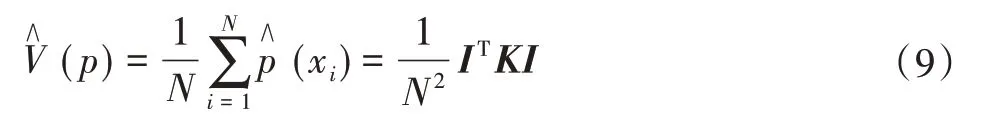
式中：I为(N×1)的单位列向量；K为维数( )N×N的核矩阵。

由式（5）和式（9）可知，瑞利熵H(p)可由样本核矩阵K求出，对核矩阵K进行特征值分解，可得：

式 中：D=diag(λ1,…,λN)为 特 征 值 对 角 阵；E=[e1,…,e n]为特征向量矩阵。

将式（10）代入式（9），得：

任一非线性映射样本φ(x)在特征向量ei的核熵投影ti可表示为:

KECA算法通过在主元空间和残差空间分别建立T2和Q统计量，一旦T2或者Q大于对应的阈值，则说明出现异常，T2统计量和Q统计量定义如下：

式中：ti为主元向量；∧-1为由选取的前A个特征值组成的对角阵的逆阵。

T2统计量阈值定义如下：

式中：Fα(A,N-A)为带有A和(N-K)个自由度、置信水平为α的F分布的临界值。

Q统计量阈值Qα定义如下：

式中：；cα为高斯分布(1-α)%的置信限。

2.3 支持向量数据描述

SVDD的基本思想是：将数据映射到高维特征空间，在高维特征空间构造一个包含几乎全部目标数据的体积最小的超球体，落在超球体内部及表面的数据则是正常数据，其余则为异常数据，该算法对数据分布无假设，并且异常监控统计量比较敏感。其原理如图2所示。

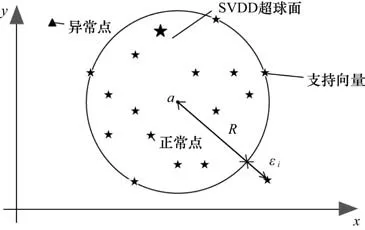
图2 SVDD模型

故SVDD的优化目标就是求一个中心为a，半径为R的超球面：

式中：x i(i=1,2,…,n)为目标数据；ξi为松弛变量；C为惩罚系数。

通过引入拉格朗日乘子αi、αj以及核策略将上式最优化问题转化为下面的对偶问题：

由式（17）、（18）得到超球体的半径满足：

式中：xk为支持向量。

若测试样本z属于目标样本集，则应满足下列条件：

故通过构造如下监控统计量以及相应控制限进行异常检测：

3 基于改进MKECA的异常检测流程

3.1 数据预处理

多批次是注塑成型过程产生的数据的主要特征之一，其包括时间、批次、过程变量三个维度，用三维矩阵X(I×J×K)表示，其中I代表批次，J代表变量，K代表采样点。在实际生产过程中，直接对三维数据建模存在困难，将三维数据利用批次-变量展开法展开为二维数据再进行建模，如图3所示。

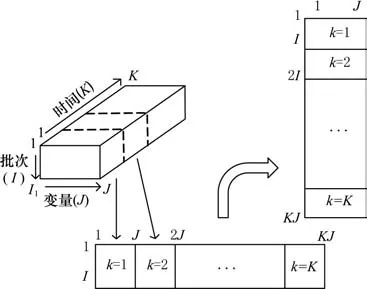
图3 三维数据展开过程

首先将注塑成型过程的原始数据X(I×J×K)沿批次展开为X(I×(K×J))，对其进行z-score标准化处理，其次将标准化后的矩阵X(I×(K×J))再沿变量方向重新排列成二维矩阵X((I×K)×J)。采用局部近邻标准化取代全局标准化对数据进行标准化处理，以解决数据的多模态特性对异常检测效果的影响。

3.2 离线建模

（1）采集注塑机正常工况下的数据作为本文所提算法的训练集；

（2）对训练集按照批次-变量法展开为二维数据；

（3）为训练集中的每个样本寻找近邻集，并对近邻集求均值和标准差，对样本进行局部标准化处理；

（4）用对局部近邻标准化处理的数据集进行特征提取，去除冗余数据，得到降维矩阵；

（5）对基于SVDD方法构造统计量，并根据公式（19）计算控制限。

3.3 在线检测

（1）采集异常工况下的数据作为算法测试集，采用与离线建模阶段相同的方法进行展开和局部近邻标准化处理；

（2）用KECA算法得到对测试数据集的降维特征空间；

（3）计算每个样本点到超球体中心的距离；

（4）根据公式（21）计算，判断其是否超过控制限。

基于改进MKECA方法的注塑成型过程异常检测流程图如图4所示。

图4 基于IMKECA的注塑机异常检测策略

4 实验与结果分析

本论文采用华南某大型注塑企业注塑成型过程中采集的数据作为实验数据，选择包括温度、压力、注射速度等多个过程变量用于建模，采集30个正常批次作为模型的训练集，每个批次包括10个变量，400个采样点。为了验证模型对异常的有效性，在200～300采样时刻引入注塑机喷嘴温度过高异常，构成异常数据集。

本文通过误报率FAR和检出率FDR对比各个算法的异常检测性能，FAR和FDR的定义分别如下：

图5～7和表1所示为各方法对注塑机异常的检测结果，根据核熵贡献率选取KECA的主元个数是6，SVDD中核函数采用高斯核函数，核宽为252，LNS的局部近邻数k取15，图中平行线代表95%置信度的阈值，MKECA采用T2和Q统计量监控注塑过程，试验结果表明：MKECA、LNS-MKECA、LNS-MKECA-SVDD三种算法都能察觉注塑机异常工况，但是T2统计量对异常不敏感，并不能检测到异常的发生，由于数据存在混合分布和多模态特性，Q统计量在异常发生阶段虽然检测到了异常的发生，但其漏报率相对较高，在异常发生前和异常结束后的异常误报率也较高。本文所提算法在数据预处理阶段，采用局部近邻标准化消除了数据的多模态结构，LNS-MKECA的异常检出率有所提高，但其忽略了数据存在的非高斯分布，检测结果仍存在一定的误报率。而采用SVDD对特征提取后的数据进行异常检测，不需要数据满足高斯分布的前提假设。相比MKECA和LNSMKECA算法，本文所提算法具有更高的检测精度，更低的漏报率和误报率。

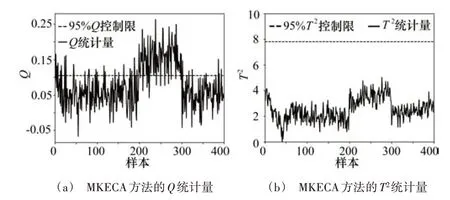
图5 MKECA方法检测结果

图6 LNS-MKECA方法检测结果

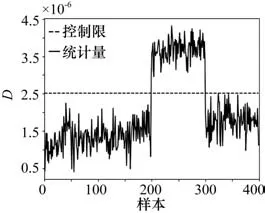
图7 IMKECA方法的D统计量

表1 不同方法的检出率和误报率

5 结束语

本文针对注塑成型过程存在的强非线性、非高斯分布、多模态等特性，提出了一种改进的MKECA算法对注塑机进行异常检测。本方法通过局部近邻标准化实现多模态数据的标准化，相比全局标准化，局部近邻标准化可以有效消除数据的多模态特性，然后采用多向核熵成分分析MKECA进行特征提取，最后，考虑到工业过程数据往往服从非高斯分布，采用支持向量数据描述SVDD建立异常监控统计量，对注塑成型过程的各过程变量进行异常检测。

通过企业采集到的数据进行对比实验，结果表明本文所提方法相比其他传统方法对异常更为敏感，具有更好的异常检测效果。