瓯江流域感潮河段潮位变化趋势分析
赵晨澄,杨友健,白直旭
(温州大学建筑工程学院,浙江 温州 325035)
1 引言
感潮河段受上游径流和外海潮汐作用,在上游洪水和下游潮水的双重影响下,其潮波特征(如潮差、潮波振幅衰减率和潮位变化趋势等)时空变化复杂。彭慧等[1]基于小清河的历年洪水与潮位同步观测资料,用定性分析和定量计算方法确定洪水与潮位遭遇最优方案,并得出超标准洪水遭遇高潮潮位的发生风险较低、高潮位遭遇中小洪水的发生风险较高的结论;吴尧等[2]基于深圳河的实测降雨、流量及水位资料,分析了潮动力作用下2018 年“0829”典型洪水的变化过程,并与同流量量级的2008 年6 月洪水进行对比,发现河道淤积、河道阻力增大和河口平均潮位抬升是导致“0829”洪水水位较高的主要原因;廖庭庭等[3]基于闽江感潮河段水动力二维模型,在不同特征流量遭遇不同特征潮位的条件下,分析了各特征点潮位流速响应关系和特征点流速与琯头潮位的响应关系,结果表明:潮位周期性变化与实测值验证成果良好,潮位与流速均呈现周期性变化,潮位变化趋势与流速变化趋势存在响应滞后现象,感潮河段特征点离入海口越远,流速滞后时间越长;黄竞争等[4]基于长江感潮河段的6 个潮位站2002 年~2014 年连续高低潮位资料及大通站月均流量数据,统计分析长江感潮河段潮波振幅衰减率、潮波传播速度及余水位坡度等传播特征值的洪枯季及沿程变化特征,结果表明潮波传播特征的洪枯季差异自上游至下游逐渐减小,径流驱动下余水位坡度引起的余水位及水深增加,导致潮波传播的有效摩擦减小,当流量超过某个阈值时潮波振幅衰减反而减弱。因此,探讨径潮动力相互作用下的潮波特征及其主要影响因素对感潮河段的工农业生产、生态环境保护、航道整治与管理、灾害防治及沿岸经济社会的可持续发展具有重要科学意义。
瓯江是温州的母亲河,保障着温州市的用水和航运,在面临台风、洪水等水文气象灾害时,又是主要的防范对象。资料表明,瓯江流域应对洪水时出现的最高水位远高于汛期平均水位,泄流量也远超过同年平均汛期水位,因此瓯江流域面临水文灾害时可能会对周边地区产生地质灾害、人员伤亡、财产损失等一系列潜在危害。本文对瓯江感潮河段江心屿水位站的水位进行分析,结合多来源数据,对上游水文过程和下游潮位过程共同影响下瓯江流域洪水的类型、驱动因素和变化趋势的综合研究,为瓯江流域的水文灾害预测和防治提供参考。
2 数据来源及分析方法
2.1 研究数据
本研究中选取瓯江流域内具有代表性的温州(江心屿)站和龙湾站的日潮位数据集和年潮位数据集[5]和瓯江上游(丽水、龙泉、青田、永嘉)和下游(朱涂、泽雅、西山、龙湾)从1970年~2019年降雨数据。
2.2 分析方法
为探讨瓯江流域感潮河段潮位变化趋势,将温州(江心屿)站和龙湾站的日潮位数据集和年潮位数据集进行统一方式处理,以期发现两个站点之间的联系;将8个站点的降雨数据,作为与潮位相关的预测数据集和验证数据集,用于潮位变化的影响因素探究,并且将降雨数据先做整体分析,再分为五个时间段[6]分别分析:Ⅰ(1970年~1979年),Ⅱ(1980年~1989年),Ⅲ(1990年~1999年),Ⅳ(2000年~2009年),Ⅴ(2010年~2018年)。使用方法包括:线性回归法、平均值计算法、MK趋势和突变检验法、Theil-Sen median方法、重现期法。
2.2.1 线性回归法
线性回归方法,主要依据水位实测数据资料,通过回归分析建立一些水位的潮位和年份的经验分析方程,用经验分析方程进行计算回归分析的结果,得出各站的离散性大小,来判断整体的波动程度和变化趋势。但是线性回归法建立的经验分析方程主要是依靠于数据资料的拟合,对于某些因素的影响考虑较小,所以对于线性回归的使用也仅仅在于部分符合使用条件的数据计算。
设定潮位数据为yi,i=1,2,……,n

在处理具体数据时,用于建立起潮位与年份之间的关系。首先判断数据之间的离散程度,判断整体的变化趋势如何,从而运用线性回归方程判断基于未来年份和洪水事件发生关系,以及判断未来年份潮位变化的趋势。
2.2.2 平均值方法
平均计算是用来计算已经整合的数据资料的平均值从而推算出未来潮位可能变化的趋势。通过平均值法以每十年为时间单位进行计算,分别计算出温州(江心屿)站和龙湾站的高低潮位平均数据,然后进行绘图比较,最终得出潮位的变化趋势和变化规律,同时也可以得出两个观测站的数据关联程度[7]。
设时间序列{y(t)}, t =1,2,3,…… ,对于任意正整数τ=1,定义均值序列:
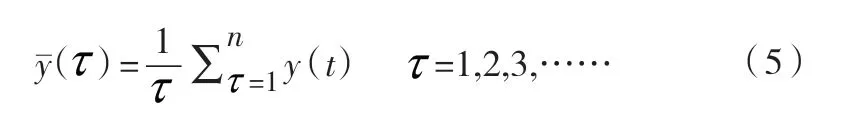
2.2.3 Mann-Kendall(MK)法
运用Mann-Kendall(MK)法,综合已知的全部数据来判断突变年限,然后以判断突变年限前后应用常规的计算方法对数据进行处理。此方法的功能强大,不需要样本遵循一定的分布,即使部分数据确实也不会影响最终的结果,不受少数异常数值的干扰,在实际使用中的适用性较强。其不但可以检验时间序列的变化趋势,而且还可以检测时间序列是否发生了突变。
对于一个时间序列Xt=(x1,x2,……, xn),MK趋势检验的统计量S计算公式如下:

如果S是一个正数,那么后一部分的观测值相比之前的观测值会趋向于变大;如果S是一个负数,那么后一部分的观测值相比之前的观测值会趋向于变小。
其中, sgn为检验函数:
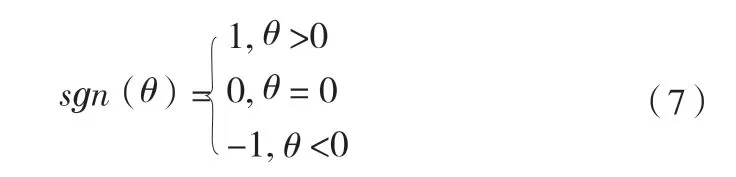
然后计算方差Var以及Z统计量

2.2.4 Theil-Sen median方法
在线性方程回归方法中涉及较多的参数,在参数的影响之下会影响最后的计算精度。在MK突变趋势的判断下,有两个时间段下的潮位变化有明显的差异,并且在已经确定的时间周期影响下,发现了潮位的高低随着时间周期的变化而产生一定量的变化。
建立以下数学模型,每年的最大高低潮位值的变化趋势数值与时间周期性变化的趋势,用来判断未来若干年后的潮位变化趋势。选取的最大高低潮位数值均为已知水文站测得的每日最大高低潮位数据,进行年平均统计得出的年平均最大高低潮位数据,然后以年为基础时间单位选取一个时间周期内的若干段整体时间单位,分析出这些整体时间段之间整体潮位的变化数值[8]。

其中j和i代表着参与计算的潮位年份, tj-ti代表着选取数据的时间段的长度(一般默认选取潮位的时间段长度一致)。
2.2.5 重现期法
在一定年代的潮位记录资料统计期间内,若干年一遇的潮位高度出现的平均间隔时间,为该潮位产生频率的倒数。在应用重现期法进行数据处理时,确定若干个不同的时间段内最大的潮位发生次数[9]。单位为年(a),重现期与频率成反比:

它带有统计平均的意义,说得更确切的一点是表示某种水文变量大于或等于某一指定值,每出现一次平均所需要的时间间隔数。
3 结果及分析
3.1 潮位变化变化趋势
首先对整体潮位的变化数据进行统计,做出变化趋势图。再以整体时间为计算区间(1970年~2018年),对整体数据进行线性规划统计,综合出各种因素对线性回归方程的影响(降雨量、地理因素、人为干预等影响)。
3.1.1 潮位变化波动
从图1来看,温州站和龙湾站的年平均高-高潮位趋势变化在1990年~2004年较为一致,在年平均低-低潮位趋势变化中,温州站基本保持显著下降趋势,而龙湾站在2000年~2014年内下降趋势显著。

图1 平均潮位趋势变化图
从图2可知,温州站和龙湾站在年最大高-高潮位趋势变化较为一致,在年低-低潮位趋势变化中,温州站的潮位变化趋势波动更为显著,且高于龙湾站的潮位变化趋势。
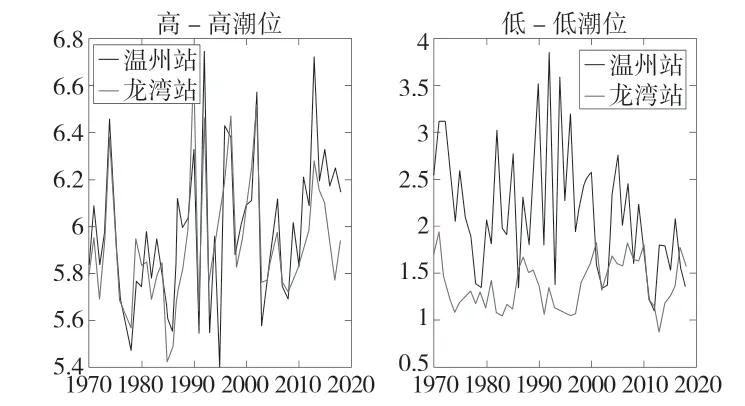
图2 最高(低)潮位趋势变化图
3.1.2 最大潮位拟合回归分析
对最大高-高潮位和低-低潮位进行线性回归拟合分析(见图3),结果可知各站的离散性较大,根据已知结果可以判断出整体的变化趋势可行度较低,证明无法对未来的最大(小)值变化结果作出正确的变化预测。
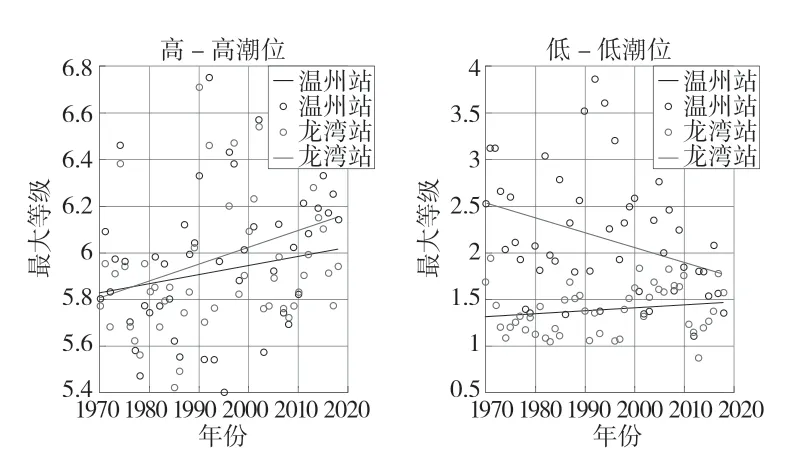
图3 潮位变化线性回归分析图(最值)
其中,高-高潮位的线性回归方程为:
y = 0.0072x-8.3870, R2=0.1055(温州)
y = 0.0039x-1.8597, R2=0.0435(龙湾)
低-低潮位的线性回归方程为:
y = -0.0159x+33.8831, R2=0.1160(温州)
y = 0.0034x-5.4119, R2=0.0372(龙湾)
对平均高-高潮位和低-低潮位进行线性拟合分析(见图 4),结果可知温州站年平均高-高潮位有显著上升的变化趋势,低-低潮位有显著下降的变化趋势。
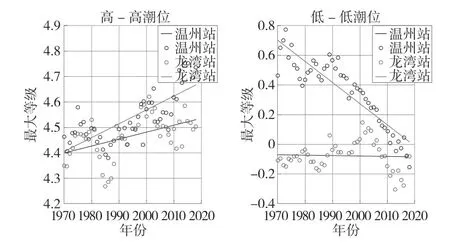
图4 潮位变化线性回归分析图(平均)
其中,高-高潮位的线性回归方程为:
y = 0.0055x-6.3848, R2=0.5911(温州)
y = 0.0027x-0.8880, R2=0.2310(龙湾)
低-低潮位的线性回归方程为:
y = -0.0143x+28.9651, R2=0.8176(温州)
y = -0.0003x+0.4450, R2=0.0016(龙湾)
根据高低潮水位数据,计算不同年份的平均高-高潮位和低-低潮位:然后计算每10年的高低潮水位平均值(见图5,图6),结果可知,对龙湾站而言,高-高潮位有小幅上升,低-低潮位呈先上升再下降的趋势。对于温州站而言,高-高潮位有明显的持续上升,低-低潮位有明显下降的趋势。年平均低-低潮位呈现下降趋势,意味着在海平面上升的大背景下,年平均高-高潮位有更大幅度上升、极端洪水事件发生的概论可能增加。

图5 龙湾站十年平均潮位图

图6 温州(江心屿)站十年平均潮位图
根据(图7、图8)可知,各年代同一站点年内高-高潮位变化规律较为相近,低-低潮位变化规律较为相近。潮位的变化趋势在各个月份之间也应该是相近的,综合考虑降水等因素的影响,其主要变化原因应该是海平面的变化。多种分析表明,高-高潮位和低-低潮位变化特征不同,但是两站的高-高潮位变化趋势相近,低-低潮位变化趋势相近。

图7 龙湾站十年变化图
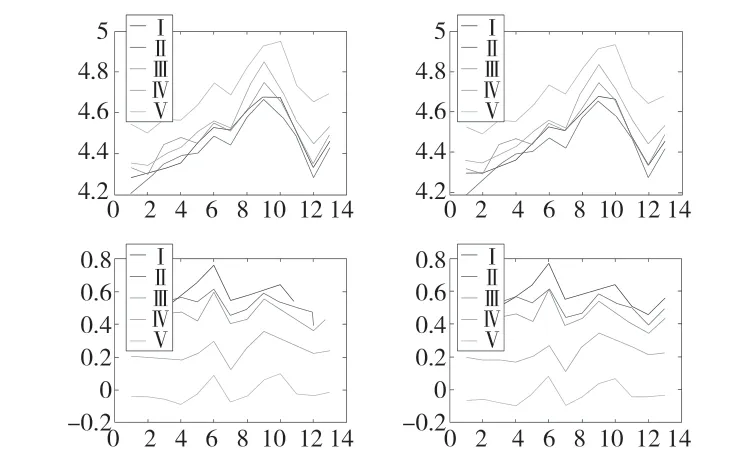
图8 温州(江心屿)站十年变化图
3.1.3 潮位之间的线性关系分析
根据图9可知,年最大高-高潮位、低-低潮位和年平均高-高潮位、低-低潮位之间相关系数较低。但温州站和龙湾站的高-高潮位最大-平均回归结果相近。

图9 潮位线性相关拟合图
其中高-高潮位的回归方程:
y = 1.3806x-0.2837, R2=0.1967(温州)
y = 1.3480x-0.0950, R2=0.1619(龙湾)
低-低潮位的回归方程:
y = 1.4520x+1.6283, R2=0.2431(温州)
y = 1.0843x+1.4685, R2=0.1608(龙湾)
3.2 突变点分析
对两站高-高潮位、低-低潮位的年均数据序列进行MK趋势检验和突变检验。由图10、图11 可知,温州站高-高潮位由上升趋势,低-低潮位有下降趋势,突变点均为2000 年。高-高潮位的上升趋势起于2000 年以前,可以认为其上升趋势是突变现象。低-低潮位的下降趋势起于20世纪70 年代,但2000 年存在突变。低-低潮位的下降趋势在2000 年前是自身变化,2000 年后可能与高-高潮位的上升相互影响,也存在突变现象。

图10 温州(江心屿)站MK趋势分析图

图11 龙湾站MK趋势分析图
龙湾站高-高潮位无显著性变化趋势,突变点为1994 年/1995 年(数据缺失年份);低-低潮位在2000 年~2010 年间有显著下降趋势,无突变点。龙湾站高-高潮位的突变时间略早于温州站,与温州站UF达到2(显著上升趋势)的时间相一致。考虑到龙湾站与温州站到相对位置,可以认为龙湾站高-高潮位的突变现象对温州站高-高潮位规律产生了响应影响。
寻找变化趋势突变的原因:瓯江干流上没有建设水库,支流有许多水库。支流水库中较大的有紧水滩水库和滩坑水库,建造时间分别为1981年~1986 年和2004年~2008年,与突变时间不一致.判断突变并非工程因素引起。
3.3 重现期结果统计
对温州站、龙湾站高-高潮位和低-低潮位的年最大潮位进行频率和重现期分析[10],结果见表1。
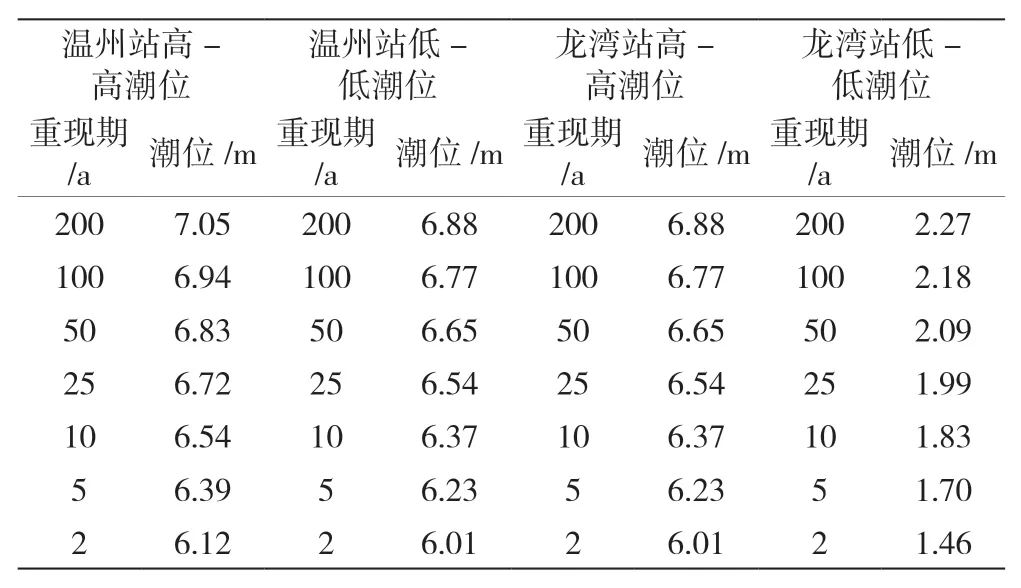
表1 两站点的年最大潮位和重现期数据
对两个站水位的洪水事件进行分析。以95%频率水位为洪水阈值。
3.4 上游流量对水位的影响分析
通过控制断面流量和温州站潮位的考虑滞后效应的相关系数(lag correlation)对河道汇流时间进行分析。流量数据为1970年~1998年。由表2 滞后效应的相关系数统计可知,河道汇流时间较短,不超过1天。上游控制断面流量对低-低潮位影响较大,不是高-高潮位大小的主要影响因素。再以龙湾站潮位为潮位驱动因素,分析温州站与龙湾站的潮位相关关系,由表3 温州站与龙湾站之间的相关关系中可知,仅温州高-高潮—龙湾高-高潮数据存在较为明显的相关关系。温州低-低潮—龙湾低-低潮数据的相关关系也不明显。温州高-高潮—温州低-低潮的同站数据相关关系也不够明显。

表2 滞后效应的相关系数统计
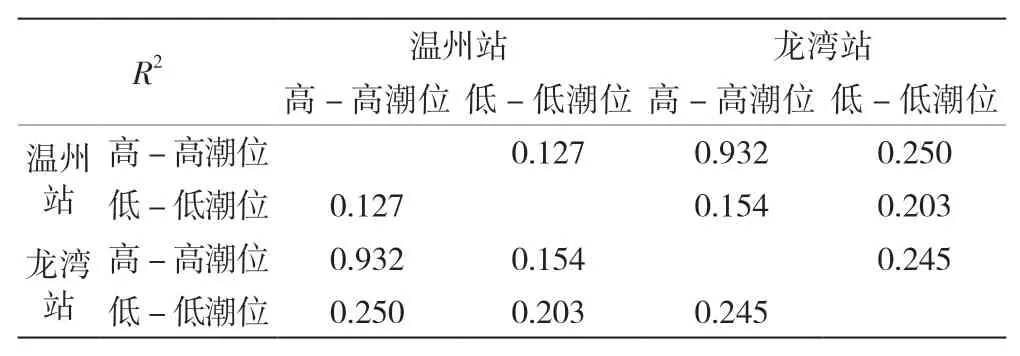
表3 温州站与龙湾站之间的相关关系
3.5 洪水天数变化趋势
根据图12可知,年洪水天数、年洪水事件数存在周期性,且有上升趋势。洪水事件时水位无明显变化。对温州站进行分段分析。1970年~1999年平均洪水天数为12.97天,平均洪水事件为4.97次,平均洪水历时2.61天;2000年~2018年平均洪水天数为26.47天,平均洪水事件为8.84次,平均洪水事件历时2.99天。

图12 高-高潮位变化图
根据图13可知,年洪水天数、年洪水事件数存在周期性,温州站有下降趋势,龙湾站无明显变化趋势。洪水事件时水位无明显变化趋势。对温州站进行分段分析。1970年~1999年平均洪水天数为23天,平均洪水事件为10.13次,平均洪水历时2.27天;2000年~2018年平均洪水天数为10.32天,平均洪水事件为4.63次,平均洪水事件历时2.23天。
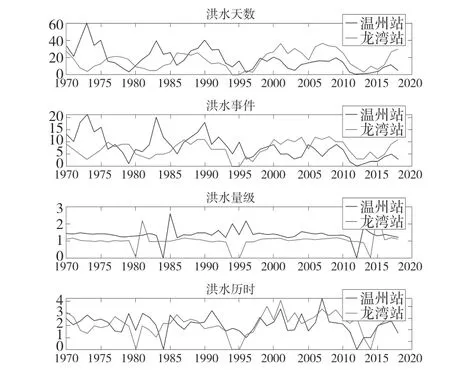
图13 低-低潮位变化图
4 结论
本文以瓯江流域的潮位变化趋势为主要研究对象,应用线性回归法、平均值计算法、MK趋势和突变检验法等方法进行了深入详实的研究。本文的主要结论如下:
1)温州站的高-高潮位是由海面潮位主要控制的,低-低潮位有其他的控制因素。这在后续的感潮河段水力学模拟中必须加以考虑。同时,这一现象似乎意味着传统研究中对感潮河段“顶托”效应的顾虑收益降低。在温州市区的防洪工作中,由于市区所临河段的高-高潮位主要受潮位控制,受上游流量影响小,因此洪水事件与高潮位叠加对于水位的升高影响有限。
2)洪水与潮位叠加事件使得低-低潮位升高。在洪水事件中,低-低潮位的升高会影响温州市区内涝排泄。因此,洪水与风暴潮(台风)综合极端事件相对于单纯风暴潮事件,沿江防洪堤(防御河道内洪水)压力升高有限;内涝排泄压力升高明显。
3)对于潮位未来趋势的分析应用,可以提前做好瓯江应对台风、洪水等水文灾害的预警工作;减少关于瓯江应对台风、洪水等水文气象灾害时产生的人员伤亡和财产损失;为其他受地形影响并且对气候变化敏感的属山溪性河流应对台风、洪水等水文灾害时提供参考数据与防治经验。

