长基线航空重力测量精度分析

李瑞，舒晴，骆遥，王晨阳，高维，周坚鑫

(1.自然资源部 航空地球物理与遥感地质重点实验室，北京 100083；2.中国自然资源航空物探遥感中心，北京 100083)

0 引言

航空重力测量是以飞机等航空飞行器为载体，结合惯性导航平台、航空重力仪、全球定位系统GPS(global positioning system)等可以在高速运动中测量重力场信息的一种地球物理调查手段[1-2]。目前，我国近海航空重力勘探已基本完成全覆盖，为海洋基础地质调查和地学研究提供了重要基础资料[3]，随着航空重力测量的发展，走向深蓝自然成为了地球物理工作者的使命之一。自2018年起，中国自然资源航空物探遥感中心(简称航遥中心)集成了国内首套中远海域航空重力测量系统，该套系统以空中国王350ER固定翼飞机为运载平台，集成俄罗斯重力测量技术公司GT(gravimetric technologies)所推出的GT-2A型航空重力测量系统，目前已完成中远海域高精度航空重力测量20余万测线千米。

航空重力作业过程中，为实现高精度GPS差分定位，需要至少1套GPS系统安装于飞机上，即GPS移动站，同时还需要在地面架设至少1套GPS参考站，即GPS基站。测绘学领域定义基线(baseline)是两测量点之间的连线[4]，在此两点上同步接收相同的GPS卫星信号，并采集其观测数据。《航空重力测量技术规范》(DZ/T 0381—2021)[5]要求全球导航卫星系统基站要布设在测区范围内，基线长度应控制200 km之内，不宜超过500 km；采用更长基线测量时，应通过试验来验证长基线能否满足航空重力测量精度的要求。而实际情况是我国具有300余万km2的管辖海域[6]，随着航空物探作业的深入，广阔的海域之上往往不具备架设基站的条件，长基线条件下的航空重力测量能否满足精度需求是首要解决的技术问题之一。

在航空重力测量过程中，作用于重力传感器上的垂向加速度干扰谱与重力信号谱相重叠，对干扰的补偿需要精确的外部信息，如差分GPS高度、速度等，GPS噪声是制约测量精度的主要因素[7]。随着基线长度的增加，差分定位精度无疑会受到影响。罗锋等[8]针对GPS基站的位置精度和选择进行了探讨，并对计算获得的航空重力异常结果进行对比分析，但其基线距离较短(约130 km)，仍无法满足中远海域航空重力测量的实际需求，且尚未对最终测量精度是否会有较大影响进行讨论。Damiani等[9]对惯性测量辅助下的长基线(400～500 km)定位在机载重力测量中的应用进行了研究，并未对差分定位精度的影响展开分析。Salazar等[10]提出了一种基于GPS参考站的速度加速度扩展解算法EVA(extened velocity and acceleration determination)确定飞机速度和加速度信息，有望应用于无GPS基站的航空重力测量。

针对中远海域航空重力测量实际，根据长基线实测数据，基于不同距离基站解算得到的航空重力异常数据结果，综合测线内符合精度评价、交叉点精度评价等多种方法，进一步分析长基线对航空重力测量精度的影响，为今后广泛开展中远海域航空重力作业提供技术支撑。

1 GT-2A航空重力测量系统解算原理

航空重力测量是利用重力仪和GPS的观测值来获取飞行器测线上的重力异常。尽管勘探领域使用的地球重力场在空间范围内被认为是位置的函数，但就航空重力测量系统而言，由于飞机飞行是沿测线进行的，重力观测序列就成为时间的一个函数[11]。因此，航空重力问题可转化为提取时间函数的重力异常的问题。

航空重力测量仪器的核心敏感元件是探测(敏感)质量SM(sensor mass)，利用其运移来感知加速度的大小。沿飞行测线的航空重力异常的基本方程是重力仪的运动在地理垂直方向上的投影方程：

(1)

G0(φ,h)=G0(φ)+ΔG0(φ,h)

,

(2)

其中椭球表面(h=0)上的重力正常场值G0(φ)可由Somigliana公式计算，

，

(3)

其中:a、b为地球的长、短半轴；Ge和Gp分别是赤道处和极点处的重力值；φ为地理纬度。

仅仅保留h/RE的线性项，则带高程的自由空气校正可以根据下式计算，

(4)

其中：RE、RN分别为地球E向和N向的曲率半径，uE为地球自转角速度。

厄缶校正项包含地球自转中的离心力与科里奥利力的总和，其校正项为：

,

(5)

其中:RE、RN分别为地球E向和N向的曲率半径;VE、VN为载体E向速度和N向速度;uE为地球自转角速度。

结合重力仪的量测方程，构建卡尔曼滤波模型[12-14]，通过卡尔曼滤波及平滑最终获得测线上的重力异常值，其中，椭球高、速度、纬度等均是滤波模型的重要输入项，对滤波精度具有直接影响。

2 GT-2A航空重力测量数据

GT-2A航空重力仪目前在我国是一种较为主流的航空重力测量仪器，自2006年航遥感中心引进以来，先后已完成数十万公里的测量工作量，工作区域涉及重要油气盆地及重点海域，其标称精度为0.6 mGal。

GPS系统由两套地面GPS基站(分别命名为Base1和Base2；Base2为主基站，Base1为备份)和机载移动站构成。经选址确定两个GPS基站位置，Base1距离测区距离为600～800 km；Base2距测区距离为300～400 km。Base1由国家基准点引点采用三点联测的方式测得，Base2由5个GPS连续运行站的数据联测得到，两个基站引点后位置精度均优于10 mm，符合规范要求的优于0.1 m的精度要求。飞行过程中两个基站先于机载移动站开机，确保差分解算时基站和移动站具有共同时间段。

数据来源于某海域实测数据。使用GT-2A后处理系统模块GTNAV和GTGRAV分别计算GPS差分解和航空重力异常值，GTNAV和GTGRAV是由莫斯科国立中央大学控制与导航实验室所开发的GT-2A航空重力仪数据后处理软件包，GTNAV模块主要功能为提供差分GPS相位解并估计重力仪三轴稳定平台的倾角；GTGRAV模块则利用GTNAV计算得到的导航数据计算测线上的重力异常值。滤波周期使用100 s，平均飞行速度为360 km/h，相应半波长分辨率为5 km[15]；使用机型为空中国王350ER型飞机，该型飞机在加装副油箱后低空最大航程达3200 km，较适宜开展长航程航空物探测量；测区主测线方向为SN方向，间距为1km；切割线方向均为EW向，间距为10 km。实测航空重力异常交叉点精度优于2 mGal。

3 差分定位影响因素分析

在卫星导航领域，PDOP值可直接反映差分定位精度的大小。PDOP(position dilution of precision)，称为三维(空间)位置精度因子，PDOP值的大小与GPS定位的误差成正比，PDOP值越大，定位误差越大，定位的精度就越低[16-17]。此外空间中运行的卫星(SV,space vehicle)个数也直接影响定位精度，规范要求参与计算的卫星数不少于5颗，PDOP值绝大多数时间应小于2.5。

仅考察测线时段，选取主基站(Base2)和备份基站(Base1)数据齐全的20条测线，利用GTNAV 模块解算出的多普勒相位解进行统计计算，测线卫星数和PDOP值统计如图1～6所示。据图1～3，Base2解算时，测线差分解算卫星数最小值均在7颗以上；Base1解算时，测线差分解算卫星数最小值均在6颗以上，两个基站解算结果卫星数平均值均在7颗以上，主基站解算卫星数总体好于备份基站。

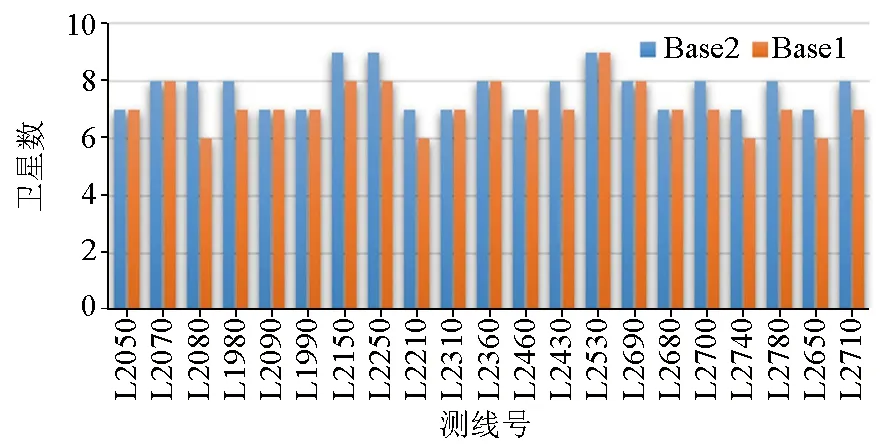
图1 测线卫星数最小值

据图4～6，据两种解算结果分析，测线PDOP值最小值均小于2，除测线2780外，PDOP平均值均小于2.5；Base1解算时，测线PDOP值均大于Base2解算结果，有6条测线PDOP值最大值明显大于Base2解算结果，备份基站解算PDOP值结果略差于主基站。

图2 测线卫星数最大值

图3 测线卫星数平均值

图4 测线PDOP值最小值

图5 测线PDOP值最大值

图6 测线PDOP值平均值

4 航空重力测量精度分析

4.1 重力异常内符合精度

由于Base1和Base2距离测区距离不同，在其他条件均不变的情况下，基于Base1和Base2差分基站的GPS差分解算结果，使用GT-2A数据处理模块GTGrav计算测线上航空重力异常；对同一测线(切割线)使用不同基站所获重力异常进行内符合精度统计[18]，结果如表1所示。

结合上节所述，尽管使用Base1解算时，PDOP值和卫星数均略差于Base2解算结果，但差分后主要参数除个别测线外仍在规范要求范围内。以测线L2780为例，其使用Base1解算时PDOP值平均值大于2.5，但不同基站解算重力异常内符合精度调整前为0.416 mGal，调整后为0.353 mGal，并未对重力异常结果产生明显影响(图1)。

由表1可知，SN向测线内符合精度调整前平均值为0.397 mGal，调整后平均值为0.323 mGal，EW向切割线内符合精度调整前平均值为0.432 mGal，调整后平均值为0.320 mGal。不同基站重力异常内符合精度统计结果表明，长基线对内符合精度的影响与短基线结果[8]相当，也就是说，长基线并未额外增大航空重力测量的误差。

表1 同一测线(L)、同一切割线(T)采用2个不同基站解算获得的重力异常内符合精度统计

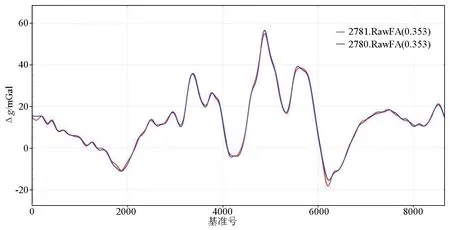
图7 长、短基线条件下测线L2780重力异常内符合精度

4.2 交叉点精度评价

航空重力测量总精度采用测线与切割线交叉点残差的均方差进行评价，即

,

(4)

式中：δi为第i个切割线与测线交叉点上的场差值N为参加计算的切割线与测线交叉点个数。根据航空重力测量技术规程，要求调平前航空重力异常总精度应优于2 mGal，实际测量精度优于该指标。

测线内符合精度评价反映了使用不同基站解算结果间的符合程度。我们选取测区SN向测线20条，EW向切割线21条，每条测线均为同一架次飞行，仅使用不同基站解算获得的重力异常来进行交叉点精度评价，以期系统反映因基线长度不同而对测区总精度所造成的影响。如表2所示，方案1切割线和测线均采用Base1计算重力异常，方案2切割线采用Base1、测线采用Base2，方案3切割线采用Base2、测线采用Base1，方案4切割线和测线均采用Base2，分别评价其交叉点精度。

表2表明，方案1、方案2和方案3精度相当,交叉点均方差均为1.3 mGal左右；当切割线和测线均使用距离测区相对较近的基站Base2计算时，精度最高，为1.21 mGal，但是方案4与方案1～3相差并不大，最大仅为0.11 mGal，相比航重总精度要求的2 mGal的量级，几乎可以忽略不计。

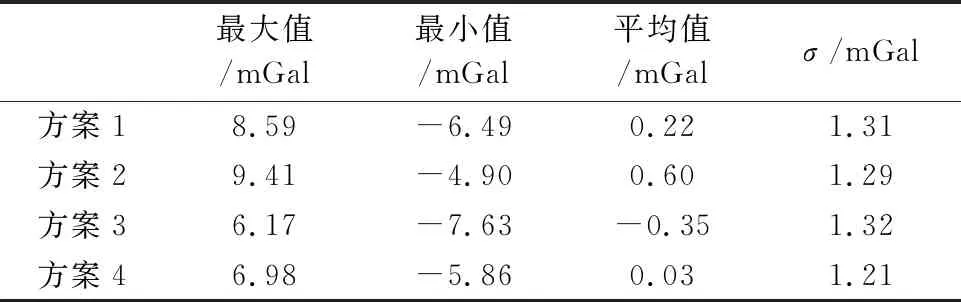
表2 航空重力异常交叉点精度评价

5 结论

针对长基线航空重力测量实际应用需求，结合实测数据，分析了因基线长度不同而对航空重力精度所造成的影响。使用远、近基站解算航空重力异常，同测线内符合精度调平前在0.4 mGal左右，调平后在0.3 mGal左右，该结果与罗锋等[8]计算结果相近。针对测区使用Base1和Base2计算得到的测线和切割线上重力异常，分别组合进行交叉点精度计算，结果显示，4种方案测区总精度相差不大，最大仅为0.11 mGal，即在基线长度在300～400 km和600～800 km条件下，且卫星数、PDOP值等满足时，航空重力测量精度受基线长度影响有限，可以开展高精度航空重力测量作业。此外，目前航空重力测量仍主要依赖于差分GPS定位技术，随着北斗技术的推广应用，在航空重力等重点领域开展基于北斗定位技术尤其是基于北斗卫星精密单点定位技术的研究和应用也迫在眉睫。