数形结合思想方法的内涵、价值及教学策略
福建省宁德市东侨经济技术开发区第二小学 肖丽梅
一、数形结合思想方法的内涵
《数学课程标准》明确指出:数学是研究数量关系和空间形式的科学。数量关系常扩展为抽象的、形式化的数学对象,如数、式、方程等,我们称之为“数”;空间形式常扩展为有形的、可视的数学对象,如图形、图像、曲线等,我们称之为“形”。“数”构成了数学抽象化的符号语言,“形”构成了数学直观化的图形语言,各有各的优势。“数”与“形”是数学中的两个最基本的研究对象,它们是有联系的,在一定条件下可以相互转化。把数学问题的数量关系和空间形式结合起来考察,根据解决数学问题的实际需要,可以把“数”问题转化为“形”的问题去讨论,或者把“形”的性质问题转化为“数”的问题来研究,利用数形相互转化、取长补短,这就是“数形结合思想”。它既是一种非常重要的数学思想方法,是一种数学意识,也是一种有效的教学方法。它在数学教学中的应用一般可分为两种情形:一是借助数的精确性、程序性和可操作性来阐明形的某些属性,即“以数解形”;二是借助形的几何直观性来阐明某些概念及数之间的关系,即“以形助数”。两者相辅相成、扬长避短。正如数学家华罗庚说过:数缺形时少直观,形少数时难入微。
二、数形结合思想方法在计算教学中的价值
计算教学是小学数学教学的重要内容之一,也是小学生必须掌握的基本技能。运算能力在2011版课程标准中作为十大核心词之一被提出,更是凸显计算教学的重要性。近年来,随着计算教学理念的不断更新,越来越多的一线教师注重引导学生在理解算理的基础上归纳算法,实现算理与算法的和谐统一。如何有效让学生理解运算背后的道理,笔者认为运用数形结合思想的第二种情形,即“以形助数”,借助小棒图、点子图、方格图等具体可感的图形可以帮助学生理解算理。其本质就是用直观的几何图形呈现抽象的算理,从而把学生的抽象思维和形象思维有机地融合起来。这样,学生理解算理就言之有物、有迹可循了。从而使学生在掌握单一的计算方法、技能的基础上感悟数学思想,加深对数学知识的规律和本质的认识,更好地将数学知识转化成数学能力,发展学生的思维能力,提高学生的数学综合素养。
三、数形结合思想方法在计算教学中的策略
(一)在低年级计算教学中利用小棒图以形助数,直观理解算理
纵观苏教版低年级的数学教材,小棒无疑是重要的学具之一,用小棒有结构地表示数,能形象表达数的组成,有助于学生感受数值。计算教学中经常采用摆小棒,能把抽象的数的运算转化成直观的物化动作,不但能得到计算结果,也蕴含了计算的过程与方法。教师在教学过程中要善于引导学生把小棒用好用活,利用小棒呈现计算过程,借助小棒图的图形语言来突破重难点,将有助于学生直观理解计算的原理。
例如苏教版一年级下册《100以内的加法和减法(二)》,这个单元中加法里的进位和减法里的退位都是十进制计数法的计数规则在计算时的具体应用。学生学习时,必须理解其进位和退位原理,懂得为什么“个位满10要向十位进1”,为什么“十位退1到个位要作10”。这既是本单元教学的重点,也是教学的难点。教学时有效进行小棒的操作,可以引导学生从形象到抽象地理解进位和退位。如教学例1:24+6时,学生会根据已有的两位数加一位数的口算思路,很自然地先算4加6得10。这时该怎么办?让他们摆小棒激活“10根小棒应该捆成一捆”的经验(如图1),形象地看出以后,再算20+10=30。这就在不进位的两位数加一位数的基础上,凸显了进位加法的特点,既加强了口算的基本思路,又解决了第一步计算的得数满10的矛盾。教学例2 :30-8时,学生看到算式也打算像不退位减法那样计算,但不知道先算几减几。这时也让学生摆小棒计算,要想从3捆中拿走8根,必须拆开1捆变成10根,从中再拿走8根(如图2),这里的拆一捆变10根就是退位减法中借1当十的直观诠释。教学两道例题都重在引导学生摆小棒,既用了教学口算时的方法,又能直观形象地表现出为什么进位或退位,与学生已有的数学活动经验比较接近。这样,进位和退位的算理更加深入人心,重难点的突破就水到渠成了。

图1
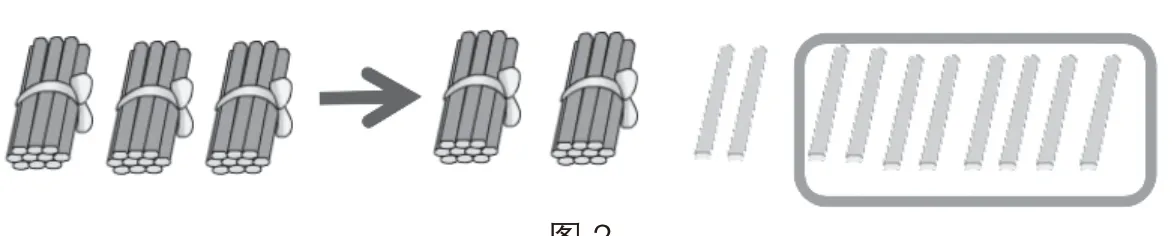
图2
又如教授苏教版二年级《乘法的初步认识》时,引导学生把相同加数连加的算式改写成乘法算式,绝大数学生能把加法“3+3+3+3+3”改写成乘法算式“5×3”或“3×5”,也能把加法算式“5+5+5”改写成乘法算式“5×3”或“3×5”,但是学生不能理解其中的道理。对此会有困惑:不同的加法算式怎么可以改写成相同的乘法算式呢?借“形”助“数”,运用数形结合的思想方法,可以帮助学生深刻理解现象背后的道理。教师可以出示一组小棒图,每行5根,摆3行。引导学生竖着看,每列3根小棒,用加法算式是“3+3+3+3+3”,表示的是5个3相加;横着看,每行5根,用加法算式是“5+5+5”,表示的是3个5相加。所以它们都可以用相同的算式“3x5”或“5x3”来表示。这是一组简单的小棒图,但可以帮助学生直观地理解乘法算式的意义,加深学生对乘法概念的理解,促进学生深度思考。
(二)在中年级计算教学中利用点子图以形助数,沟通理解算理
中年级计算教学主要以整数乘、除法为主。教材除了两位数乘或除以一位数依然沿用小棒图来帮助学生理解算理外,更多的例题是引导学生在解决实际问题的数量关系中理解算理、感悟算法。对于思维水平还处在具体运算阶段的中年级学生来说,如果能在分析数量关系的基础上也用图形语言来帮助理解算理,无疑是锦上添花的教学。
如教授苏教版三年级下册《两位数乘两位数》,这节课是整数乘法学习过程的关键环节之一,具有很强的基础性。例3的教学重在意义建构两位数乘两位数笔算的竖式,理解为什么分两步乘,以及每一步乘的结果为什么要写在规定的位置上。教学时首先让学生想办法解决实际问题,收集能够建构竖式的解法。两位数乘两位数的算法,其本质是应用乘法分配律,把两位数乘两位数分解成两位数乘十位数和两位数乘一位数,并把两部分的结果相加。三年级学生没有学过乘法分配律,不可能联系运算律来理解两位数乘两位数的算法,只能联系实际问题中数量关系来感悟算法。例题已知每箱南瓜24个,12箱一共有多少个?列出算式24×12后,交流算法时应突出“萝卜”卡通的想法,即结合情境图给的启发:已经搬来10箱,还有2箱正在搬,可以先求10箱和2箱各有多少个,再合起来。接着利用这种算法构建乘法竖式,联系解决实际问题的步骤,具体讲述竖式的结构及其原理,有序展示竖式的形成过程(如下图)。

教学不该到此为止,教师还需思考如何运用图形语言沟通竖式计算的算理,让学生体验由算理直观化到算法抽象化的过程,巧妙运用点子图来探索可将这一过程具体形象地表现出来。出示点子图,引导学生在图中圈出点子表示竖式计算的过程(如图3),这样就将学生抽象的思路外显化。指 出24×2=48、24×10=240、48+240=288 分别在图的哪里?针对教学中的难点“240 中的 4 为什么要写在十位上,1 为什么写在百位上,能在点子图上找到它的位置吗? ”用问题串充分勾连了点子图与竖式之间的联系引发学生深度思考。
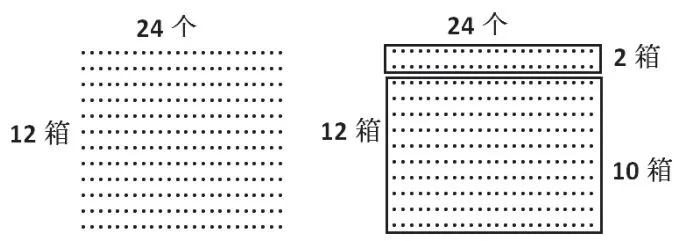
图3
在此基础上提炼出竖式的计算步骤与每一步的计算内容,从而归纳算法,可以将竖式过程修改如下:

这样将点子图的圈一圈与乘法竖式计算一一对应,沟通了直观操作与抽象算理之间的联系,使“先分后合”与乘法竖式计算的基本思路融为一体,让学生明确了笔算两位数乘两位数就是用第二个乘数个位和十位的数依次与第一个乘数相乘,然后再把积相加。正因为通过点子图把数形结合思想巧妙渗透,它就像一座桥梁,把“冰冷”的口算和“神秘”的竖式算理紧密地联系起来, 使学生在不知不觉中知其然更知其所以然。
(三)在高年级计算教学中利用方格图以形助数,深化理解算理
高年级的计算教学主要以小数和分数为主,其中小数的计算是建立在整数的基础上进行的,它们的计算原理有很大的相似性。而在有关分数计算的教学中,我们通常会利用画方格图来引导学生观察、比较,从中发现内在的联系、规律,从而既直观又深刻地理解计算的原理,提高计算的能力。例如苏教版数学六年级上册《分数乘分数》这节课,教学时先出示例4,引导学生经历“看图—写式—求积”的过程,感受“分子相乘、分母相乘”的可能性。接着出示例5,引导学生通过“看式—画图—求积”体验“分子相乘、分母相乘”的合理性。
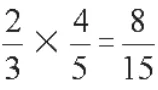
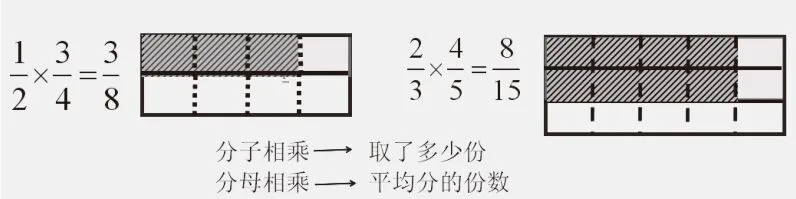
图4

总之,在计算教学中,利用数形结合思想可将复杂问题简单化、抽象问题具体化,是教学中常用的数学方法。适当运用数形结合思想对帮助学生理解算理、掌握算法有着举足轻重的作用。在计算教学中,充分挖掘计算教学的核心内容, 将数形结合思想渗透于具体的数学问题中,在让学生解决问题中正确理解算理,掌握算法,帮助学生积累用数形结合方法解决数学问题的数学活动经验,组织引导学生对以形助数的简洁性进行评估反思,不断优化学生的思维品质。都说“授之以鱼 ,不如授之以渔”,方法的掌握、思想的形成 ,才能最终使学生受益终生。让我们每一位教师都能巧妙运用数形结合思想方法帮助学生理解抽象的数学知识,引领学生顺利走进数学的神奇殿堂。

