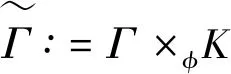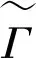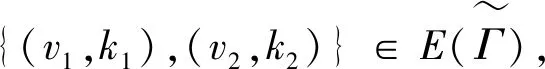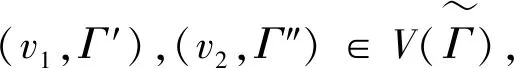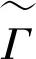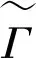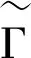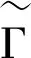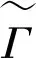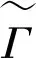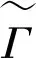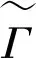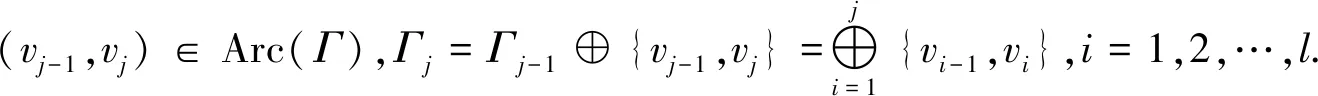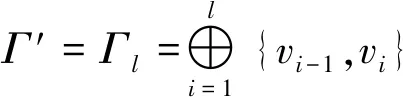圈空间及其应用*①
徐尚进
(广西大学,广西 南宁 530004)
本文所讨论的问题属代数图论研究领域,所涉及的图均为简单无向图.
代数方法一直是图论研究的重要手段.比如利用图的全自同构群可以研究图的某种传递性,利用图的邻接矩阵则可以研究图的谱,等等.用代数方法研究图还包括研究其边空间和圈空间,这部分内容在不少图论文献[1,2,3,4]中都有介绍.然而所给的定义不都完全相同,并且对边空间的描述也不够严谨.本文主要讨论图的边空间特别是圈空间,通过完善边空间的定义来得圈空间的精准结构,最后将有关结论应用于边覆盖图.
1 预备知识
本节给出本文所需要的一些基本概念、性质和结论.
1.1 简单无向图
为了给出简单无向图的严格定义,我们先引进以下记号.
定义1.1设V是非空集合.分别记V的所有有序对的集合为
V(2)∶={ (u,v)|u,v∈V,u≠v} ;
V的所有无序对的集合为
V{2}∶={ {u,v}|u,v∈V,u≠v} .
注:所谓无序对{u,v},意味着{u,v}={v,u}.
直接计算可知,当V是有限集时有
|V(2)| = |V| ( |V|-1) ,|V{2}| = |V| ( |V| -1 ) /2.
接下来给出简单无向图的定义.
定义1.2一个(有限)简单无向图Γ是由其(非空)顶点集合V={v1,v2,…,vn}和一个边的集合E⊆V{2}决定.边集E中的无序对{v,u}称为图Γ的无向边,顶点v和u称为该边的端点.顶点的个数称为图Γ的阶,记作|Γ|.
具有顶点集V和边集E的图Γ通常记作Γ=(V,E).反之,图Γ的顶点集和边集又分别记作V(Γ)和E(Γ).
每条无向边{v,u}对应着两个序相反的有序对(v,u)与(u,v),称为Γ的弧.弧是有方向的,比如弧(v,u)的起点和终点分别是v和u.Γ的弧集记作Arc(Γ).
由于无向图Γ的每条边都对应着一对方向相反的弧,因此有
性质1.3|Arc(Γ) |=2|E(Γ)|.
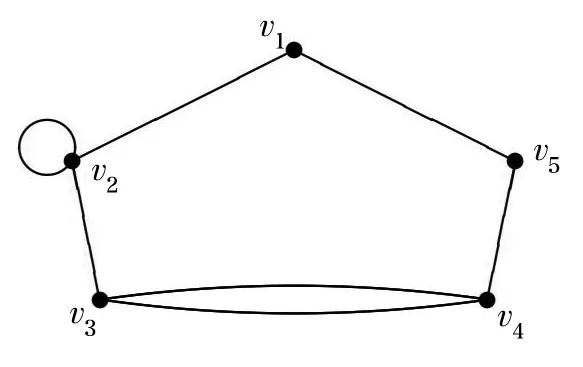
图1
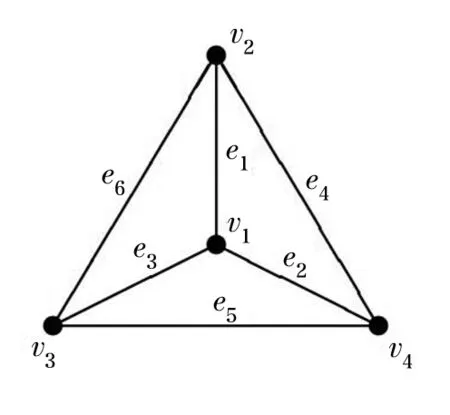
值得一提的是,简单无向图不能有自环(即端点同一的边)或重边(即两条边的端点对应相同).例如图1中,有一条端点同为顶点v2的边,属自环;还有两条都以顶点v3和v4为端点的边,属重边.这些在简单图中都不能有.
围绕简单无向图还有如下基本概念.
定义1.4设Γ=(V,E)是一个简单无向图.
(1) 与v∈V相邻的顶点个数称为v的度,记作deg(v),与v相邻的顶点集合称为v的邻域,记作N(v).
特别地,度数为0的顶点称为孤立点;度数等于同一个常数k的图称为正则图,k称为该正则图的度数,记作Val(Γ).
(2) 如果V′⊆V,E′⊆E∩V′[2],则称Γ′=(V′,E′)为Γ的子图.进一步,如果V′=V,E′⊆E,则称Γ′是Γ的支撑子图;如果V′⊆V,E′=E∩V′[2],则称Γ′=(V′,E′)为V′的导出子图,记作[V′].
(3) 如果Γ的一个由两两不同顶点组成的序列v0,v1,…,vk满足{vi-1,vi}∈E(i=1,2,…,k),则这个顶点序列称为Γ的一条路,详称k-路,记作[v0,v1,…,vk],其中k称为这条路的长.而长大于2且首尾相等的k-路[v0,v1,…,vk-1,vk=v0]称为k-圈,简称圈,记作Ck.
(4) 在顶点集合V中定义关系“~”:v~u当且仅当存在从v到u的路,易知“~”是等价关系.我们把每个等价类的导出子图称为Γ的一个连通分支.如果Γ只有一个连通分支,则称Γ是连通图.此时,Γ中任意两个顶点之间至少存在一条路.
性质1.5设Γ是简单无向图,则Γ的边数
(1.1)
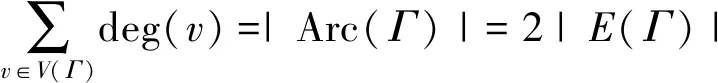
本文还涉及简单无向图的自同构群以及由它建立起来的传递性,有关概念详见文献[5].
1.2 树
定义1.6[6]连通无圈的简单无向图称为树.以树为连通分支的图称为林.
性质1.7[6]设Γ是简单无向图,则下列各项等价:
(1)Γ是树;
(2)Γ的任意2点之间有且仅有一条路;
(3)Γ连通且|Γ|=|E(Γ)|+1;
(4)Γ无圈且|Γ|=|E(Γ)|+1.
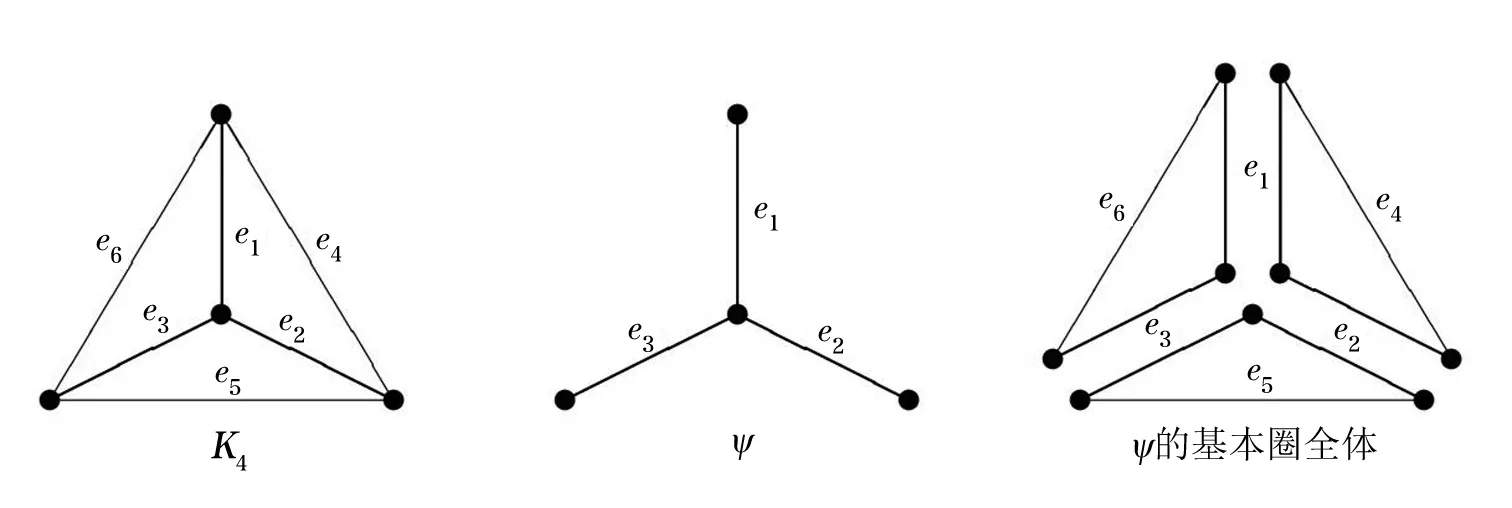
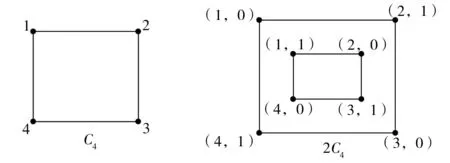
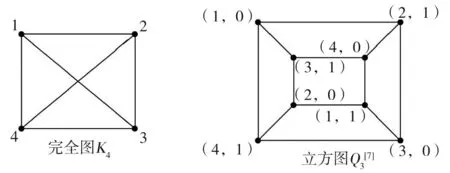
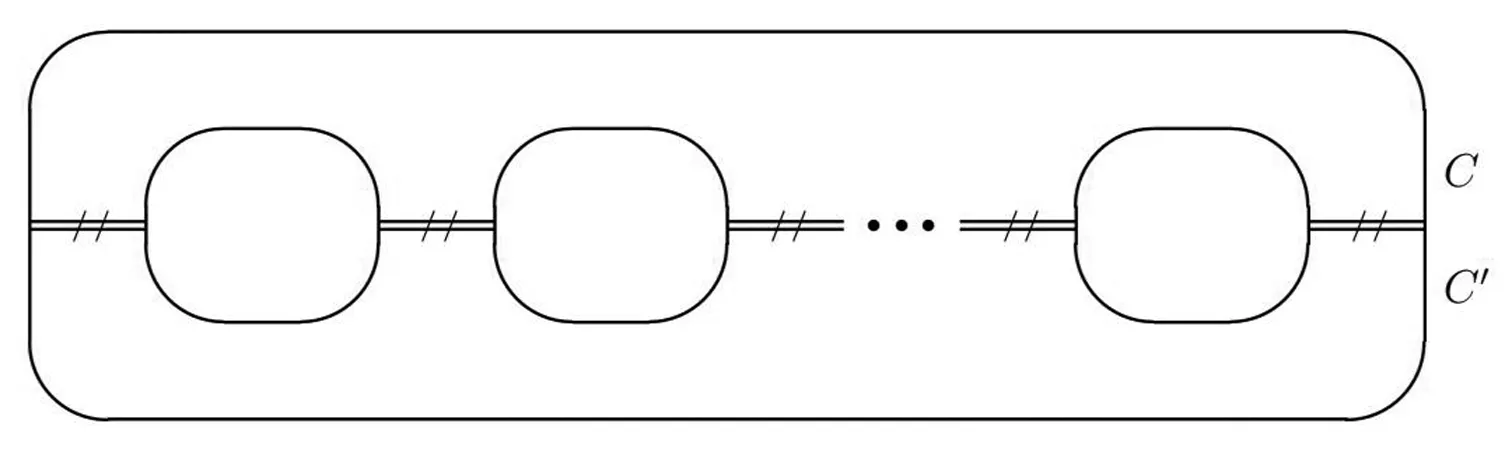
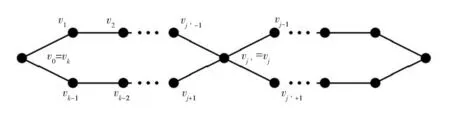
证明(1)⟹(2)由Γ连通,则Γ的任意2点v,u之间至少存在一条路,设为[v0=v,v1,v2,…,vk-1,vk=u].假设v,u之间存在另一条路[u0=v,u1,u2,…,ul-1,ul=u],则先取i是使vi≠ui的最小正整数.易知i (2)⟹(3)Γ显然连通.为证明|Γ|=|E(Γ)|+1,可对|Γ|用归纳法.事实上,当|Γ|=1时,由E(Γ)=∅,得1=|Γ|=|E(Γ)|+1.结论成立.假设结论对于顶点数小于|Γ|的图成立.由于Γ的某2点之间仅有一条路,故Γ在删去该路的一条边后被分割为两个连通分支Γ1和Γ2.这时,|Γ1|+|Γ2|=|Γ|,|E(Γ1)|+|E(Γ2)|=|E(Γ)|-1.再由归纳假设,|Γi|=|E(Γi)|+1,i=1,2.从而|Γ|=|Γ1|+|Γ2|=|E(Γ1)|+|E(Γ2)|+2=|E(Γ)|+1. (3)⟹(4)只需证Γ无圈.假设Γ含有一个k-圈Γ′,则圈Γ′上共有k个顶点和k条边.再由|Γ|=|E(Γ)|+1>k,可知Γ′之外还有|Γ|-k个顶点.往证|Γ|-k≤|E(Γ)|-k.为此,定义V(Γ)V(Γ′)到E(Γ)E(Γ′)内的一个对应:∀v∈V(Γ)V(Γ′).由于Γ连通,故存在v到Γ′的最短路[v,v′,…,v″],其中v″∈V(Γ′).这时{v,v′} ∉E(Γ′),于是可令v对应{v,v′}∈E(Γ)E(Γ′).显然这样的对应是单射,因此|Γ|-k≤|E(Γ)E(Γ′)|=|E(Γ)|-k,导致|Γ|≤|E(Γ)|,与(3)矛盾.从而(4)成立. (4)⟹(1)只需证Γ连通.假设Γ不连通,则可增加k>0条边使之连通且无圈,这个新图记作Γ′.这时V(Γ)=V(Γ′),|E(Γ′|=|E(Γ)|+k.往证|E(Γ′)|≤|Γ′|-1.为此,先取定v∈V(Γ′),然后定义E(Γ′)到V(Γ′){v}内的一个对应:∀{v′,v″}∈E(Γ′),由于Γ′ 连通且无圈,因此d(v′,v)≠d(v″,v).当d(v′,v)>d(v″,v)时,规定{v′,v″}对应于v′.这时v′≠v,且Γ′的不同边所对应的顶点也不同,说明该对应是E(Γ′)到V(Γ′){v}内的单射,因此|E(Γ)|+k=|E(Γ′)| ≤|Γ′|-1=|Γ|-1,推出|E(Γ)|+1≤|Γ|-k<|Γ|,与(4)矛盾.从而只能有Γ连通.□ 推论1.8设Γ是树,则Γ至少存在2个1度顶点. 给定一个简单无向图Γ=(V,E).为方便研究,其边集相同的子图视为等同(即不计较子图的孤立点),无边的子图(即空图)记作∅.若Γ的边集E={e1,e2,…,em},则Γ的子图Γ′可对应于2元域GF(2)上m维向量空间V(m,2)的一个向量(x1,x2,…,xm),其中 反之,V(m,2)的任意一个m维向量(x1,x2,…,xm)也可对应于Γ的一个子图Γ′ ,其中E(Γ′)={ei|xi=1}⊆E.由此,Γ的子图共有|V(m,2)|=2m个. 例1.94阶完全图K4具有顶点集V(K4)={v1,v2,v3,v4}和边集E(K4)={e1,e2,…,e6}(见图2). 图2 又设V(m,2)的向量(x1,x2,…,xm)和(y1,y2,…,ym)分别对应Γ的子图Γ′和Γ″,则向量(x1+y1,x2+y2,…,xm+ym)对应的子图称为Γ′与Γ″的环和,记作Γ′⨁Γ″.这时,Γ的子图全体关于环和运算⨁以及如下定义的数乘运算·: 0·Γ′ = ∅,1·Γ′ =Γ′, 构成2元域GF(2)上的m维线性空间,称为图Γ的边空间,记作E(Γ). 性质1.10设Γ′,Γ″∈E(Γ),则 (1)E(Γ′⨁Γ″)=E(Γ′)∪E(Γ″)E(Γ′)∩E(Γ″), (2)Γ′=Γ″⟸⟹Γ′⨁Γ″=∅. 证明(1) 设子图Γ′和Γ″分别对应V(m,2)的向量(x1,x2,…,xm)和(y1,y2,…,ym).由 即得 e∈E(Γ′⨁Γ″) ⟸⟹e∈E(Γ′)E(Γ″)∪E(Γ″)E(Γ′)⟸⟹ e∈E(Γ′)∪E(Γ″)E(Γ′)∩E(Γ″). (2) 由(1)推出,Γ′=Γ″⟸⟹E(Γ′)=E(Γ″)⟸⟹E(Γ′⨁Γ″)=∅⟸⟹Γ′⨁Γ″=∅.即证得(2).□ 圈在图的研究中扮演重要角色.它与树的关系既对立(见定义1.7)但又有所关联.先看一个关于圈数的基本结论. 引理1.11设Γ是连通无向图,则Γ至少有|E(Γ)|-|Γ|+1个圈. 证明对|E(Γ)|用归纳法. 当|E(Γ) |≤ 2时,图Γ无圈.再由性质1.7,即得|E(Γ)|-|Γ|+1=0,结论成立.当|E(Γ)|>2时,如果Γ无圈,则同上理结论也已成立.如果Γ有圈,则将删去该圈一条边后的子图记作Γ′.显然Γ的圈要比Γ′的圈至少多出1个.另一方面,由于Γ′仍然连通,并且|Γ′|=|Γ|,|E(Γ′)|=|E(Γ)|-1,因此由归纳假设,Γ′至少有|E(Γ′)|-|Γ′|+1=|E(Γ)|-|Γ|个圈.从而Γ至少有|E(Γ)|-|Γ|+1个圈.□ 推论1.12设Γ是连通无向图.若|E(Γ)|=|Γ|,则Γ有且仅有1个圈. 证明根据定理1.11,图Γ至少有|E(Γ)|-|Γ|+1=1个圈.假设Γ有2个不相等的圈C和C′.不妨设C′有一条边不在C上,并记Γ′为Γ删去该边后的子图,则Γ′有圈C并依然连通.但|Γ′|=|Γ|=|E(Γ)|=|E(Γ′)|+1,导致Γ′是树(性质1.7),与前述矛盾.说明Γ只有1个圈.□ 定义1.13连通无向图Γ的一个支撑子图Ψ如果是树则称为支撑树.这时,Ψ的边称为Ψ的树枝,而E(Γ)E(Ψ)中的边称为Ψ的连枝.支撑树Ψ添加一条连枝后有且仅有一个圈(由推论1.12),称为Ψ的基本圈.基本圈作为子图自然都含于Γ的边空间E(Γ). 以下是4阶完全图K4和它的一棵支撑树Ψ及其基本圈.Ψ的树枝集为{e1,e2,e3},连枝集为{e4,e5,e6}. 图3 性质1.14设Γ是连通无向图,则 (1)Γ的支撑树通常不唯一,除非Γ本身是树; (2) 每棵支撑树的连枝条数等于|E(Γ) |-|Γ|+1,因此与支撑树的选择无关; (3) 每棵支撑树的基本圈个数等于|E(Γ)|-|Γ|+1,因此也与支撑树的选择无关. 证明(1) 显然. (2) 任取Γ的一棵支撑树Ψ.先由性质1.7,得|Ψ|=|E(Ψ)|+1.再由V(Ψ)=V(Γ),即得Ψ的连枝条数|E(Γ)E(Ψ)|=|E(Γ)|-|E(Ψ)|=|E(Γ)|-|Ψ|+1=|E(Γ)|-|Γ|+1. (3) 由基本圈的定义及(2)立得. 定义1.15设Γ是连通无向图,C1,C2,…,Cr∈E(Γ)是Γ的某棵支撑树的基本圈全体,即r=|E(Γ)|-|Γ|+1,则E(Γ)的子空间〈C1,C2,…,Cr〉称为Γ的圈空间,记作C(Γ). 性质1.16C1,C2,…,Cr是线性无关的,因此dimC(Γ)=r,|C(Γ)|=2r. 设Γ是一个简单无向图,K是一个群.如果存在Arc(Γ)到K的一个映射φ满足 φ(v,u)=[φ(u,v)]-1,(v,u)∈Arc(Γ), 则称φ是图Γ的一个K-链.若映射φ平凡,即对所有(v,u)∈Arc(Γ),有φ(v,u)≡1,则φ显然是图Γ的一个K-链,称为平凡K- 链. 覆盖图明显具有以下性质. 例1.20[7]设Γ是简单无向图.取K∶=2={0,1},并对Γ的每条弧(v,u)∈Arc(Γ),定义φ(v,u)≡1(对合).则映射φ是Γ上的一个2-链,并且覆盖图2是具有二部划分(V(Γ),0)与(V(Γ),1)的二部图,称为Γ的双覆盖图.比如,当Γ=C4时,覆盖图(不再连通,见图4).又比如,当Γ=K4时,覆盖图2同构于立方体图Q3(见图5). 图4 图5 引理2.1(1) 若C和C′是E(Γ)的圈,则C⨁C′或者是空图,或者是若干个边不交的圈之并. 证明(1) 只需考虑圈C与C′不等,并且它们的边集有交的情况.这时,边的交集只能是若干条不相连的路.当C与C′取“环和”运算之后,这些路被去掉(见图6),而C与C′各自剩下的若干条不相连的路之间一一对应,即可组成一些边不交的圈. 图6 (2) 对k用归纳法.当k=0时,Γ′=∅,结论成立. 图7 引理2.2(1) C (Γ)中非空子图是若干个边不交的圈之并; (2) 如果Γ的子图Γ′∈ E(Γ)是若干个边不交的圈之并,则Γ′∈ C (Γ). 由于简单无向图Γ的边空间E(Γ)关于子图的“环和”运算是方次数为2的加群,因此可取K∶=E(Γ)来构造非平凡的K-链. 定义3.1[7]设Γ是连通无向图,取K∶=E(Γ),并且很自然地定义Arc(Γ)到K内的映射 性质3.2[7]沿用上述记号,并令G∶=Aut(Γ),则G与K的(外)半直积GK是边覆盖图的自同构(子)群.特别地,如果Γ是点传递图,则亦然. 证明先定义σ∈G在K=E(Γ)上的作用 这时,∀Γ′,Γ″∈E(Γ),(Γ′⨁Γ″)σ=Γ′σ⨁Γ″σ,即GAut(K).根据群论知识,存在G与K的半直积GK∶={(σ,Γ′)|σ∈G,Γ∈K},其乘法关系如下: (σ′,Γ′)(σ″,Γ″)=(σ′σ″,Γ′σ″⨁Γ″). 再定义半直积GK在边覆盖图顶点集上的作用 (v,k)(σ,Γ′)∶=(vσ,kσ⨁Γ′),(σ,Γ′)∈GK. 推出(σ,Γ′)∈GK保边,因此是边覆盖图的一个自同构.即G 定理3.3沿用定义3.1的记号. [(v,∅)=(v0,Γ0),(v1,Γ1),(v2,Γ2),…,(vl,Γl)=(u,Γ′)] , 其中(vj-1,vj)∈Arc(Γ),Γj=Γj-1⨁{vj-1,vj},j=1,2,…,l.这时Γ″⨁Γj=Γ″⨁Γj-1⨁{vj-1,vj},j=1,2,…,l.从而 [(v,Γ″)=(v0,Γ″⨁Γ0),(v1,Γ″⨁Γ1),(v2,Γ″⨁Γ2),…,(vl,Γ″⨁Γl)=(u,Γ′⨁Γ″)] 是顶点(v,Γ″)到(u,Γ′⨁Γ″)的一条路. ⟸ 同理可证(略). (3) 分两种情况. (i)v∈V(C).由(2)立得. (ii)v∉V(C).此时存在顶点v到圈C的一条路L:[v0=v,v1,…,vl],其中vl∈V(C). [(v,∅)=(v0,Γ0),(v1,Γ1),(v2,Γ2),…,(vl,Γl)=(v,Γ′)], 注:文献[7,p152,Theorem 19.5]也就类似的结论给出了证明,但不够严谨.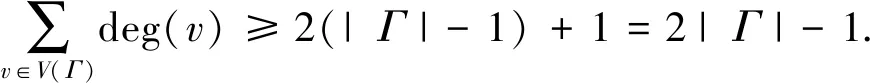
1.3 边空间
1.4 圈空间
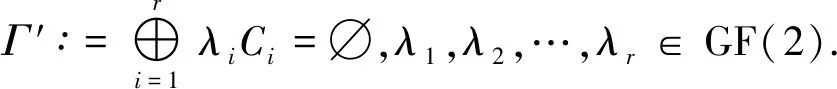
1.5 覆盖图
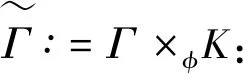
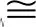
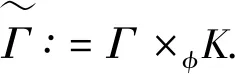
2 有关引理
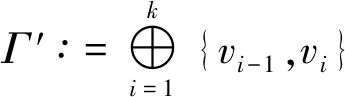
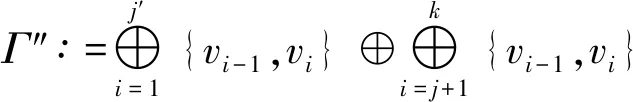
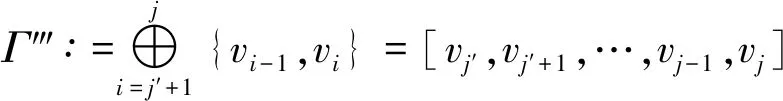
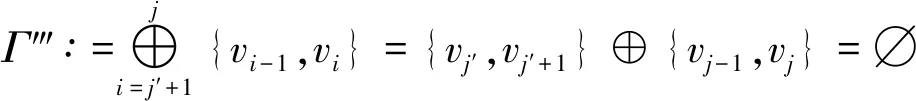
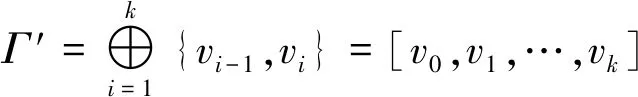
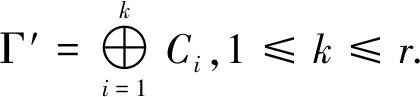
3 主要结论