中国、新加坡初中数学课程标准中的核心素养比较研究

陈碧芬，金蓓霜

随着课程与教学改革的深入推进，我国基础教育正经历从“知识至上”到“素养本位”的转变。在此背景下，教育部围绕学科核心素养从课程目标、内容结构等方面对高中数学课程标准进行了优化和修订。作为高中教育的基础，义务教育阶段的课程标准对数学学科核心素养的要求有必要进一步落实，以期考虑学生的持续发展和终身发展。[1]一直以来，新加坡的数学教育处于国际领先地位。[2]Ibrahim等人研究发现，尽管新加坡数学课程包含的内容比马来西亚少，但其学生的数学素养却优于马来西亚。这说明数学素养的内容和要求不能只关注知识本身，还需从多个角度进行分析，Safrudiannur等人的研究也证实了这一点。[3]新加坡2013年开始实施的教学大纲MathematicsSyllabusesSecondaryOnetoFourexpresscourse[4](以下简称MMS)提出以“数学问题解决”为核心的五大学科核心素养，其内容和要求不仅仅体现在课程的框架理念上，更是反映于具体的教学目标、教学内容之中。鉴于此，本文以初中数学为例，对我国《义务教育数学课程标准(2022版)》[5](以下简称CCM)和新加坡MMS中课程理念、课程目标、教学目标与教学内容进行文本的定性和定量对比分析，以期为我国数学课程改革进一步深化提供思路。

一、中国与新加坡初中数学课程设计理念与总目标的比较

新加坡的教学大纲包含了跨越 12年的数学课程，小学6年，中学4—5年以及大学先修班2年。其中，中学阶段的课程学习相当于中国的初中教育。与中国课标在初中阶段仅设置了一种统一标准不同的是，MMS按等级划分包含了O水平和N水平两类标准。O水平标准适合大多数普通学生，该标准下的考试相当于我国的中考，而N水平标准则适用于成绩优异的学生。

从课程的设计理念来看，新加坡的这种“分流”制度，是它实行“精英教育”的一种有效措施，满足了国家对不同层次人才的需要。我国数学课程的基本理念之一是“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”，体现的是义务教育阶段数学课程的基础性、普及性和发展性，且这种发展是学生的个性发展。

从数学课程的总目标看，MMS指出O水平标准下的数学课程旨在使学生“获得继续学习数学或者其他学科的数学概念和技能；通过运用数学方法解决数学问题，发展学生的数学思维，培养其推理、沟通、应用和元认知技能；通过应用数学建立数学与其他学科之间的联系，增强对数学的信心和兴趣”。不难发现， MMS将总体目标定位在学生数学问题解决能力的培养，并强调数学的工具性与应用性，要求学生能够运用数学知识解决实际问题和其他学科的问题。而CCM中的课程总目标立足于核心素养，集中体现数学课程育人价值，使学生逐步会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界，培养学生对数学的好奇心和求知欲，形成质疑问难、自我反思和勇于探索的科学精神。由此看到，两国的课程总目标在设置上大体相同，均重视基本知识和技能的培养，重视数学的自身价值与科学价值，并将“终身学习”的理念贯彻于标准之中。此外，MMS更注重学科的思维发展、元认知技能的提升，这一点在CCM中并未明确提到。

二、中国与新加坡初中数学课程核心素养的比较

(一) CCM与MMS核心素养中的构成要素

核心素养是由知识、技能、价值观、态度和意志等组成的实体。[6]CCM中给出了数学核心素养的主要表现与内涵，而MMS中给出了数学核心素养的构成要素。[7]两者可以在一定程度上相对应。本研究将从数学核心素养的“构成要素”入手比较分析两国数学核心素养的异同。MMS提出了关于数学学科核心素养的五边形模型(如图1)。该模型将“数学问题解决”看作是数学学科核心素养发展的载体，并在此过程中促进学生数学概念、数学技能、数学过程、数学态度和元认知能力的发展。数学概念可以广泛地分为数值、代数、几何、统计和分析，而要深刻理解数学概念及思想需让学生沉浸于各种学习经验活动之中，使具体经验与抽象的概念相联系。数学技能则指数值计算、代数运算、空间可视化、数据分析等，学生对这些技能的理解与掌握的前提是理解数学概念和原理，而不仅仅只是作为程序性的操作。数学过程是指在获取和应用数学知识过程中所涉及的过程技能，包括推理、交流和联系、思维技能、应用与建模。这里的联系是指数学思想之间、数学与其他学科之间、数学与现实之间能够看到并建立联系的能力，有助于学生理解数学知识。元认知是指意识到并有能力控制一个人的思维过程，学生应有机会接触、解决非常规的开放性问题，讨论并反思问题解决的进展，必要时作出改变。态度是指对数学学习的情感，包括信念、兴趣、自信心、毅力等，这些都是由学生的学习过程或经历所决定。这五个部分相互关联，相互影响，是数学学习和问题解决的重要组成部分，也是数学学科核心素养构成的核心要素。

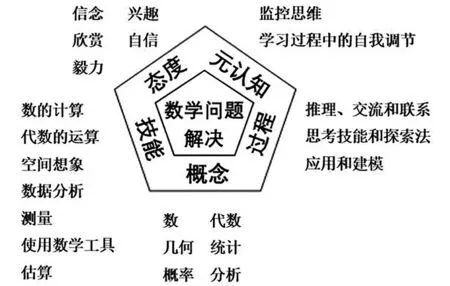
图1 MMS中数学核心素养的五边形模型

CCM中提出了初中阶段的核心素养，主要表现为抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。为了更好地对比两国涉及的数学核心素养之间的差异，试将CCM的核心素养表现融入MMS的要素体系中。对比来看，MMS将“问题解决”作为素养发展的重心，且被看作是数学核心素养发展的载体；CCM虽未明确提出“问题解决”的概念，但“问题解决”却贯穿于整个核心素养发展的始终。这在一定程度上反映出两国的教育理念不同。新加坡追求从具体问题情境入手发展学生的素养，而我国更追求素养发展的“有机统一”。但这样的“有机统一”可能会导致核心素养要素间交叉的情况，例如“问题解决”中包含“数学思考”中的实验、猜想与证明等，在一定程度上不利于后续评价学生核心素养的落实，各项指标间存在重叠。因此，对CCM进一步修订时，需构建相对独立而整体统一的框架，使得数学核心素养真正融入数学学科的课程内容之中。

(二)CCM与MMS核心素养在内容标准中的体现

CCM与MMS中的内容标准是对核心素养在下位课程目标中的落实与讨论。为了更好地进行对比，结合CCM与MMS的总目标与设计思路，将CCM与MMS中关于数学核心素养的要素划分统一为五个方面的内容:

(1)数学概念理解能力(T1):数、代数、几何、统计、概率、分析等概念的理解。

(2)数学技能(T2)：数感与数的计算、符号意识与代数运算、空间观念、几何直观、数据分析、使用数学工具。

(3)数学过程能力(T3)：数学推理能力、数学模型思想与建模。

(4)元认知能力(T4)：思维监控能力、自我调节能力。

(5)态度、交流与表达能力(T5)：信念、兴趣、信心、交流、表达。

由于每一条“内容标准”既包含了知识类型，又包含了认知过程，因此可以根据名词/名词短语划分知识类型，根据动词/动词短语判断认知目标水平。建立核心素养与内容标准的对应，则可据此判断所蕴含的核心素养。首先，在安德森划分的知识维度[8]的基础上，借助吴刚教授关于知识的分类(事实性知识、方法性知识、价值性知识)，[9]将内容标准中的数学知识类型划分为事实性知识、概念性知识、方法性知识、价值性知识、元认知知识。其次，根据PISA 2012数学测评框架将数学过程划分为3个维度：表达数学情境，应用数学概念、事实、程序并进行推理，阐释、应用和评估数学结果。[10]结合安德森划分的认知加工维度和数学认知过程的特点，将内容标准中的数学认知目标划分为识记、理解、应用、数学推理、数学评估、数学创造6个水平。需要说明的是，这6个水平并不是严格的层级关系，但达到低水平认知是达到高水平认知的基础，并且识记、理解、应用被认为是低水平认知要求，数学推理、数学评估、数学创造则属于高水平的认知要求。

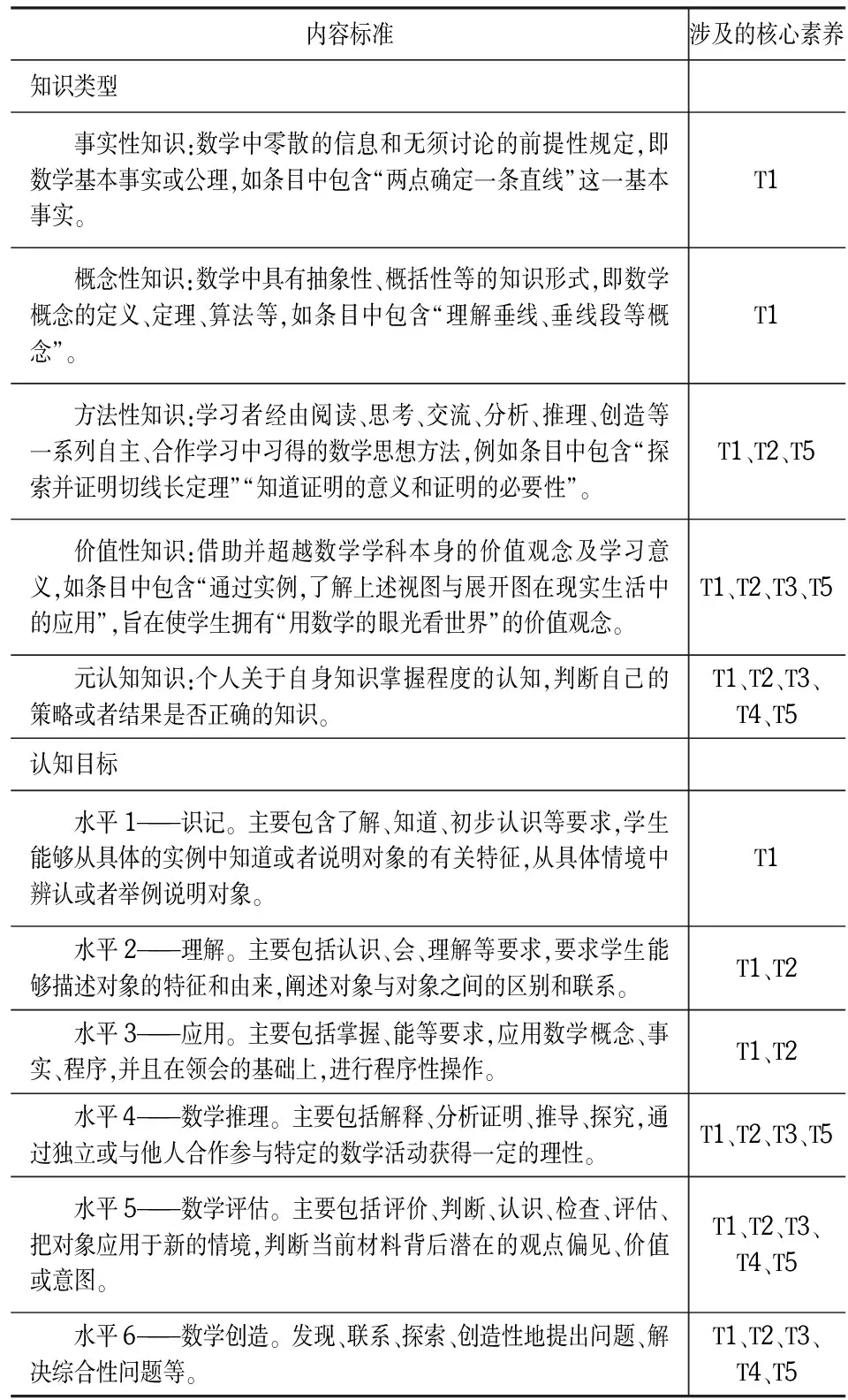
表1 初中数学内容标准涉及的核心素养

基于表1，结合CCM和MMS内容描述，将“主题领域”调整为“数与代数”“图形与几何”“概率统计”“其他”。其中“其他”包含了CCM中的“综合与实践”、MMS中的“数学过程”，由于“其他”模块认知目标贯穿在前面三大主题中，故不作单独讨论。 在此基础上，将“主题领域”再细分成具体的核心内容群，其中“数与代数”主题领域包含“数与式”“方程与方程组”“函数”三个核心内容群；“图形与几何”主题领域包含“图形性质”“图形与变化”“图形与坐标”三个核心内容群；“概率与统计”主题领域包含“数据分析”“事件的概率”两个核心内容群。

Porter认为，地形图的优势是能够通过区域清晰地看到两个维度的比重差异。[11]本研究绘制了“核心内容群—知识类型的”二维地形图(图2)，横坐标代表核心内容群，纵坐标代表知识类型，从左到右依次表示CCM和MMS。该图中的每个颜色图案代表一个比例间隔，且比例间隔在横、纵坐标的交叉点才有意义，在其余区间没有意义。在地形图上，黑色区域表示最高的比例(0.6—0.8，或60%—80%)，灰色区域其次(0.4—0.6，或40%—60%)。同样的，黑色区域、白色区域的分布百分比依次下降了8%。例如在CCM中，概念性知识与函数的交叉点处于黑点区块，说明函数中的概念性知识占比达到了(0—0.2，或0—20%)。

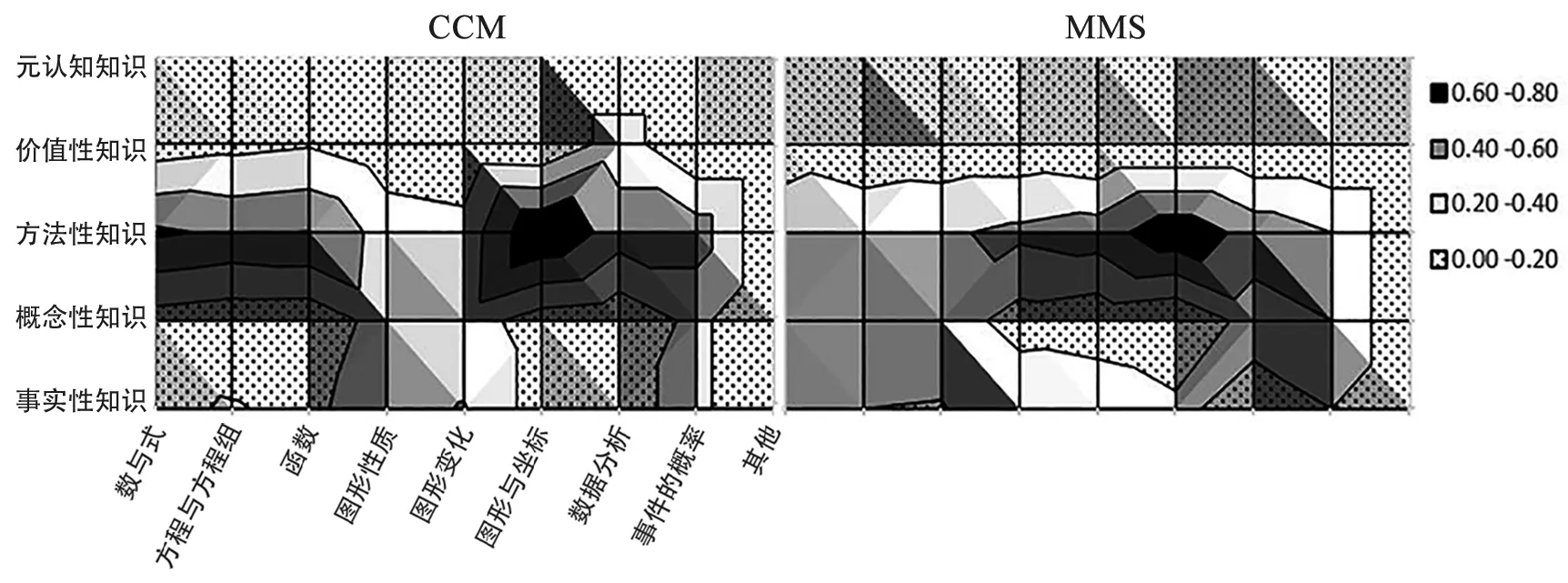
图2 核心内容群的知识类型分布

由图2可知，两国在各个主题领域均注重事实性知识、概念性知识、方法性知识，其中方法性知识在各个领域的占比最大。这一特征符合学生数学学习的特点。数学学习实际上就是对数学知识的理解和对思想方法的掌握与运用，数学思想方法是对数学知识的概括，也是数学知识的本质所在，同时体现了对数学核心素养T1、T2、T5的重视。此外，CCM在各个领域均缺失元认知知识的要求，而MMS在各个领域均对元认知知识的要求有所涉及。由此可以看出，CCM中缺少对于T4素养的具体要求。从具体的核心内容来看，CCM、MMS分别在数与式、方程与方程组、函数三个核心内容的知识类型分布无显著性差异。而在图形与几何这一领域，CCM中图形与几何的概念性知识占比大于MMS，其中一个重要的原因在于CCM对于几何课程更为重视，涉及的概念性知识点相对MMS要多。 在概率与统计这一领域， MMS比CCM更强调概念性知识的掌握，CCM则更关注概率与统计相关知识自身的价值与意义,而不仅仅关注对概念本身的学习，这与CCM强调的数学回归生活的理念是一致的。此外，CCM的价值性知识主要集中于数据分析。

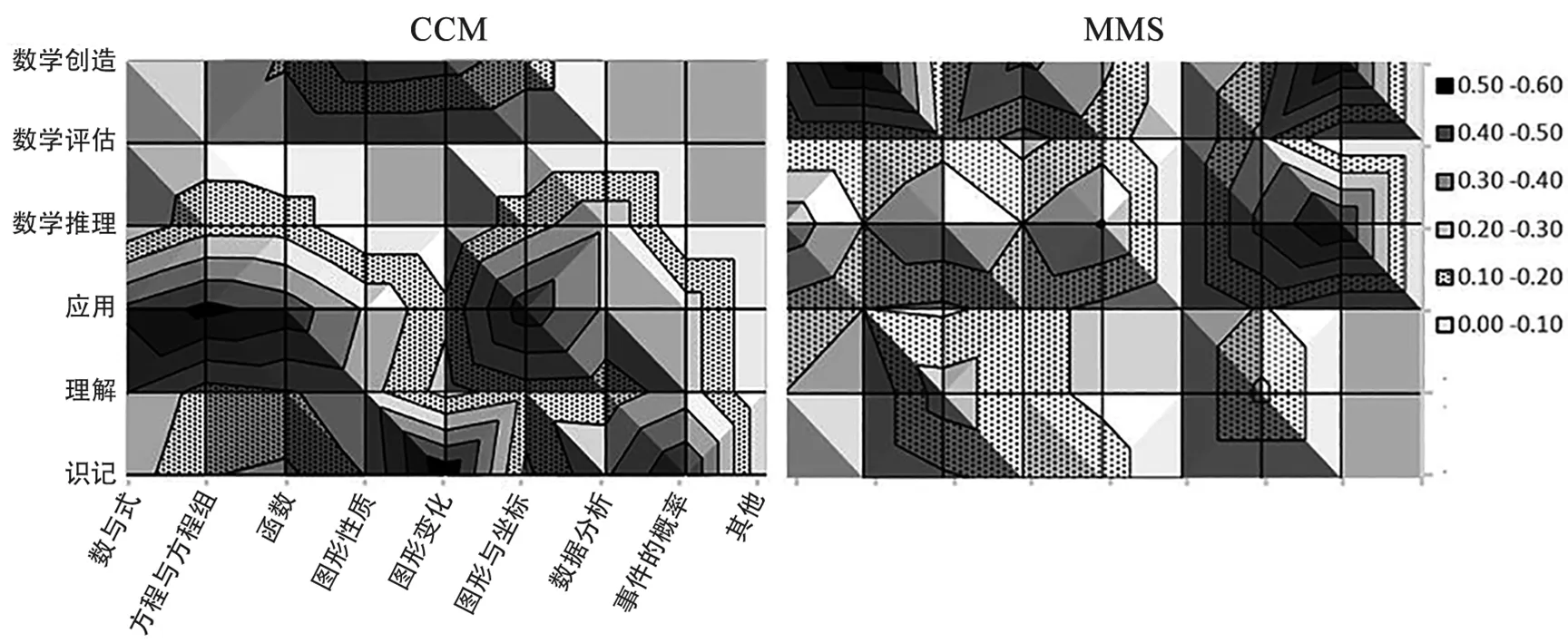
图3 核心内容群领域的认知水平分布

由图3可知，两国在认知水平要求总体上存在较大的差异。中国低认知水平要求远超过高认知水平要求，基本集中于“应用”水平及以下，而新加坡的认知水平要求主要集中于“数学推理”水平及以上。这反映了CCM在认知水平目标要求中对数学核心素养T3、T4、T5的要求没有MMS高。虽然CCM在数学核心素养的表述中也强调了“数学推理”“创新意识”“创造”，但在具体的内容标准中却没有明确的描述。CCM对于“数学评估”这一水平的认知目标要求几乎没有涉及，反映了中国数学课程对于学生自我检查与反思的关注还不够，对元认知能力(T4)这一素养的要求不够重视。在MMS中明确表示在数学问题解决的过程中掌握元认知的知识，从而监控个人的学习，[12]但CCM却没有明确的相关表述。

从数与代数的核心内容群来看，CCM中数学创造水平主要分布在函数(0.1—0.2)。这与函数作为数与形结合的数学概念，在内容上的复杂性和思维水平的高要求相吻合。在图形与几何领域，相较于CCM其他领域而言，其认知要求有所提高，主要体现在数学推理和数学创造水平的认知要求占比较大，且与MMS认知要求无显著性差异，说明两国在该领域均重视对数学创造能力的培养。在概率与统计这一领域，CCM缺少对数学评估和数学创造这两个水平的要求，分布不均衡。

三、讨论

从普遍意义上看，数学课程标准是对数学课程理念、性质、价值等作出的具体描述，它是数学课程建设的基本规范和行动准则。在数学核心素养成为国际教育的焦点之际，对中国与新加坡初中阶段数学课程标准进行审视和思考，可以得到如下思路。

(一)数学核心素养应既“有机统一”又“相互独立”

随着课程改革的不断深化，发展中国学生核心素养已成为不可忽视的话题。同时这也对数学课程提出了新的挑战。在2017年版的高中课程标准中已明确提出“数学学科核心素养”，并将课程标准围绕“学科核心素养”进行了编排与整合，为教育实践中落实核心素养提供了理论指导。义务教育阶段课程标准也已明确指出数学核心素养，在理解和推进数学核心素养在课程改革中的深化时，第一，围绕某一教学载体培养数学核心素养，使得教师在落实数学核心素养时有切实可行的途径。例如新加坡以“数学问题解决”为载体，进而形成了五大核心素养。第二，数学核心素养不应仅仅局限于从数学学科本身的学习出发给人带来的发展，还应将学生的整体发展素养置于数学学科之中，即鲍建生等人[13]所提出的数学核心素养应当包含“学科专门素养”和“学科化学生发展素养”。例如新加坡建构的五大核心素养中，“数学概念”“数学技能”“数学过程”即为学科专门素养，“态度”“元认知能力”则为学科化学生发展素养。第三，数学核心素养的要素应当在“有机统一”基础上“相互独立”，这有利于后续进行核心素养的落实与测评。

(二)在知识类型的完善与认知要求的提高中全面落实核心素养

首先，适当增加元认知知识在内容标准中的占比。元认知知识在问题解决过程中起着统摄作用，拥有丰富元认知知识的学生能够有意识地调控解题方向，对学生数学素养与能力发展的影响是深刻的。[14]目前，CCM的课程总目标中有“培养学生质疑反思的学习习惯”等表述，在一定程度上体现了对元认知的要求，但在内容标准中却未作出具体要求。实际上，在内容标准的表述中可以适当合理地添加元认知要求，如将CCM中“能用反比例函数解决简单实际问题”的要求改为“能用反比例函数解决简单实际问题，并检查过程的正确性与合理性”。这样一来，教师不仅仅关注了对学生知识技能的培养，还能够通过“反思”“批判”等策略培养学生的元认知意识和能力，进而发展学生的核心素养。具体到教学活动中，便可以此为依据设置“你是怎么想的？”“你的解题过程是否合理？”“你的方法是否为解题最佳途径？”等问题来提示学生作出反思与质疑。

其次，适当提高认知内容标准的认知要求。从具体的分析来看，初中学段数学内容标准的认知要求主要集中于“识记”“理解”“应用”等水平，在重视学生知识储备和技能应用的同时对于学生思维能力和创新能力的关注还需加强，从而促进学生数学推理与建模能力(T3)的提升。具体而言，CCM应将“数学评估”水平纳入各个主题领域，并提高“数与代数”“概率与统计”这两个领域中“数学创造”水平的占比，促进元认知能力(T4)的发展。例如在各个领域中适当增加一些类似于“运用图形的对称性、旋转、平移进行图案设计”等实际操作的要求，以及类似于“运用多种方法证明某一命题，评价并表达自己或他人方法正确性”等问题解决的要求。

对中国和新加坡课程标准进行比较，可以让我们从国际的视角来审视我国课程标准中数学核心素养设置，可为我国数学课程改革的进一步深化以及实际教学提供一些线索。