可更换构件铁路高墩抗震性能研究

高泽亮,夏修身,黄耀斌,史 军

(兰州交通大学 土木工程学院,甘肃 兰州 730070)

0 引言

传统高墩采用延性设计方法[1-2],允许结构利用塑性变形耗散地震能量,但震后桥墩会因为塑性铰的形成而产生残余变形。残余变形引起的桥墩轻微损伤可以被修复,但修复部位的承载力很难预测,若桥墩发生严重损伤,拆除重建将耗时耗力且交通中断,不利于灾后救援。因此,避免桥墩在地震中发生严重损伤或损伤时可以快速恢复使用功能至关重要。

基于可恢复功能防震理念,研究人员从结构体系上将地震可恢复功能结构分为三类,即设置摇摆构件的结构体系、自复位结构体系和设置可更换构件的结构体系[3]。摇摆及自复位桥墩利用在桥墩中合理配置体外预应力,形成自恢复体系,可以有效减小震后残余变形[4]。但受高阶振型影响,自复位桥墩仍会在墩柱中部区域形成塑性铰[5],并且由于桥墩在地震中摇摆,导致桥梁抗倾覆能力下降,从而不利于抗震。设置可更换构件的新型桥墩,通过可更换构件的塑性变形集中耗散地震能量,从而使墩柱低损伤或无损伤。国外方面,文献[6]对旧金山—奥克兰海湾大桥中塔杆间的可更换钢连接进行试验分析,研究结果表明钢连接可以有效减小塔杆主体的位移与弯矩,在小震及中震时钢连接保持弹性,强震作用下钢连接通过塑性变形耗散地震能量。文献[7]提出将可更换耗能装置连接于墩柱之间,试验中分别采用剪切钢板连接与防屈曲支撑连接,结果表明两种连接方式均明显提高了桥墩的刚度,使墩柱在强震作用下保持弹性状态。国内方面,文献[8-9]研究结果表明,强震作用下,结构中的可更换构件集中耗能,主体结构的地震响应明显减小,震后通过构件的可更换,可以使结构快速恢复使用功能。国内多将可更换机制应用于各种复杂高耸框架结构,但对于带有可更换构件的桥梁则研究较少。

本文针对一种新型可更换构件铁路高墩结构,建立全桥非线性分析模型,为充分考虑地震动不确定性因素,沿横桥向输入357条地震波进行增量动力分析(IDA),揭示了新型高墩中钢桁架杆件的损伤模式,基于IDA分位曲线探究了墩柱可能产生塑性铰的数量及位置,采用易损性曲线考察了墩柱最不利截面的损伤超越概率分布规律,并对墩柱进行基于概率性的抗震性能评估。

1 新型高墩结构及有限元分析模型

新型可更换构件高墩主要由四根墩柱及墩柱之间的钢桁架组成,见图1。墩柱位于截面的四角,是新型高墩的主要构件,采用钢筋混凝土材料。钢桁架杆件为次要构件,其功能为使四个墩柱形成一个整体,提供初始刚度、以保证铁路行车舒适。小震作用下处于弹性状态、强震作用下次要构件为耗能构件,震后其可修复或更换[10]。

图1 可更换构件高墩结构示意Fig.1 Schematic diagram of high pier with replaceable members

1.1 工程背景

以某铁路预应力混凝土连续刚构桥为工程背景,其5号桥墩为柱-板式桥墩、高为105 m,见图2。根据自振周期等效的原则,新型高墩用钢桁架替换5号主墩墩柱之间连接的薄壁板和横梁,见图3。墩柱与钢桁架通过在墩柱中预埋螺栓先与连接构件连接,然后钢桁架再与连接构件采用高强度螺栓连接,各杆件之间则通过在特定位置上打孔,采用高强度螺栓连接,以此保证震后可更换工作切实可行。新型桥墩中布设了七排钢桁架,直线段与曲线段的钢桁架间距分别为10 m与7.5 m。钢桁架从上向下分别为第一排～第七排,其杆件的截面尺寸示于图4。

图2 桥型立面布置图(单位:cm)Fig.2 Elevation layout of bridge(Unit:cm)

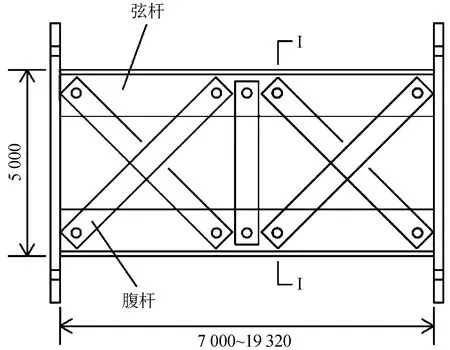
图3 钢桁架杆件示意图(单位:mm)Fig.3 Steel truss member(Unit:mm)

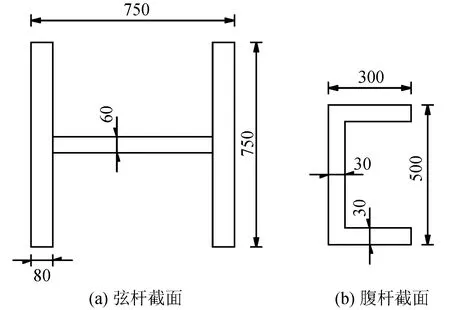
图4 钢桁架杆件截面示意(单位:mm)Fig.4 Section of steel truss member(Unit:mm)

1.2 动力分析模型

基于OpenSees平台建立新型高墩桥梁的动力分析模型,主梁采用弹性梁柱单元模拟,墩柱与钢桁架杆件均采用纤维截面梁柱单元模拟。钢筋与混凝土分别采用steel01和concrete01本构模型号。主梁与3号及7号边墩为活动约束、采用EqualDOF command模拟,主梁与4号、5号、6号墩为刚构连接、采用RigidLink command模拟。模型的墩、梁边界条件列于表1。不考虑桩-土作用、墩底固结约束。借助OpenSees平台对模型的特征值进行分析,将全桥的前十阶自振频率、周期与振型特征列于表2。

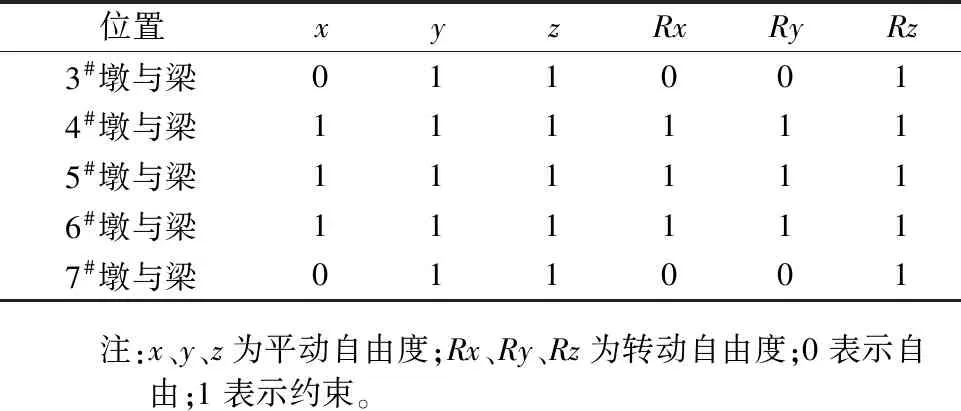
表1 全桥墩、梁边界约束条件Table 1 Full bridge boundary constraint of pier and beam

表2 自振周期和振型Table 2 Natural vibration periods and modes

2 基于IDA的地震易损性分析方法

2.1 IDA法

IDA方法可以逐级展现结构在地震作用下的弹塑性演变过程,预测地震需求与结构能力之间的关系。参考文献[11],本文选取峰值加速度(PGA)作为地震动强度指标,墩柱材料应变作为损伤指标。

2.2 极限状态

为评估墩柱的抗震性能,需要在IDA分位曲线及易损性曲线上定义墩柱各种性能水平下的极限状态。参考文献[12,13],以应变为量化指标,定义墩柱各极限状态列于表3。

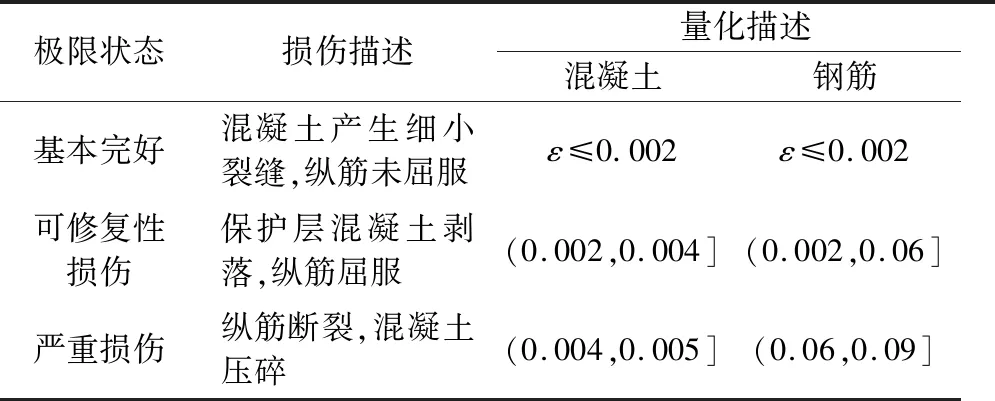
表3 极限状态定义Table 3 Definition of limit state

2.3 地震易损性分析

鉴于能力需求比模型的非线性拟合法在保证计算精度的前提下,同时还可以有效减小回归曲线的离散性,故本文采用能力需求比模型的曲线拟合法,计算公式如下[14]:

(1)

λ=a[ln(PGA)]2+bln(PGA)+c

(2)

(3)

式中:Pf为结构达到对应极限状态的超越概率;Sd为结构对应极限状态的地震反应需求;Sc为结构对应极限状态的抗震能力;λ为结构达到极限状态的需求能力比对数回归均值;σ为标准差;a、b、c为回归系数;Sr为各离散点对于回归曲线的残差平方和;n为离散点个数。

基于IDA的地震易损性分析步骤如下:

(1)建立动力分析模型。(2)选择21条强震记录,并将每条地震动的PGA调幅到0.1g～1.6g之间,步长为0.1g,使其能够达到分层细化结构弹塑性演变过程的目的。(3)分别记录每条地震波下的IM与DM值,绘制IDA曲线簇。(4)绘制50%、84%和16%概率分位曲线,并在曲线上定义极限状态点。(5)对IDA数据回归分析,建立墩柱地震需求概率模型。(6)计算各设防水准下达到极限状态的失效概率,绘制以PGA为自变量的地震易损性曲线。

3 地震动输入

对于IDA法,研究表明10～20条地震动记录可以对结构抗震性能评估达到一定的精度[15]。高墩结构易于近断层地震动中的长周期速度脉冲效应产生共振现象,从而较容易激发高墩的高阶振型效应[16]。鉴于此,本文从美国太平洋地震研究中心选取21条震中距均小于15 km,PGV与PGA分别大于20 cm/s和0.2g的近断层地震记录,用以探讨可更换构件高墩结构在近断层地震动下的地震反应特征。IDA分析时将21条地震动记录进行调幅,每条地震波由0.1g调幅至1.5g、步长为0.1g,并在9度各级设防水准下进行专门调幅,得到357条地震波,21条地震动记录的反应谱如图5所示,其基本信息列于表4。由于该桥墩的顺桥向与横桥向结构布置相近,但对全桥墩而言,主墩的顺桥向与梁体固结、其地震反应具有连续刚构桥的特点,即墩顶与墩底均有较大地震弯矩、墩柱中部区域中会出现反弯点,这会使得顺桥向高墩的高阶振型反应效应减弱,因此本文选择沿横桥向输入来研究此高墩。并对其沿横桥向进行逐一输入。

图5 加速度反应谱Fig.5 Acceleration response spectrum

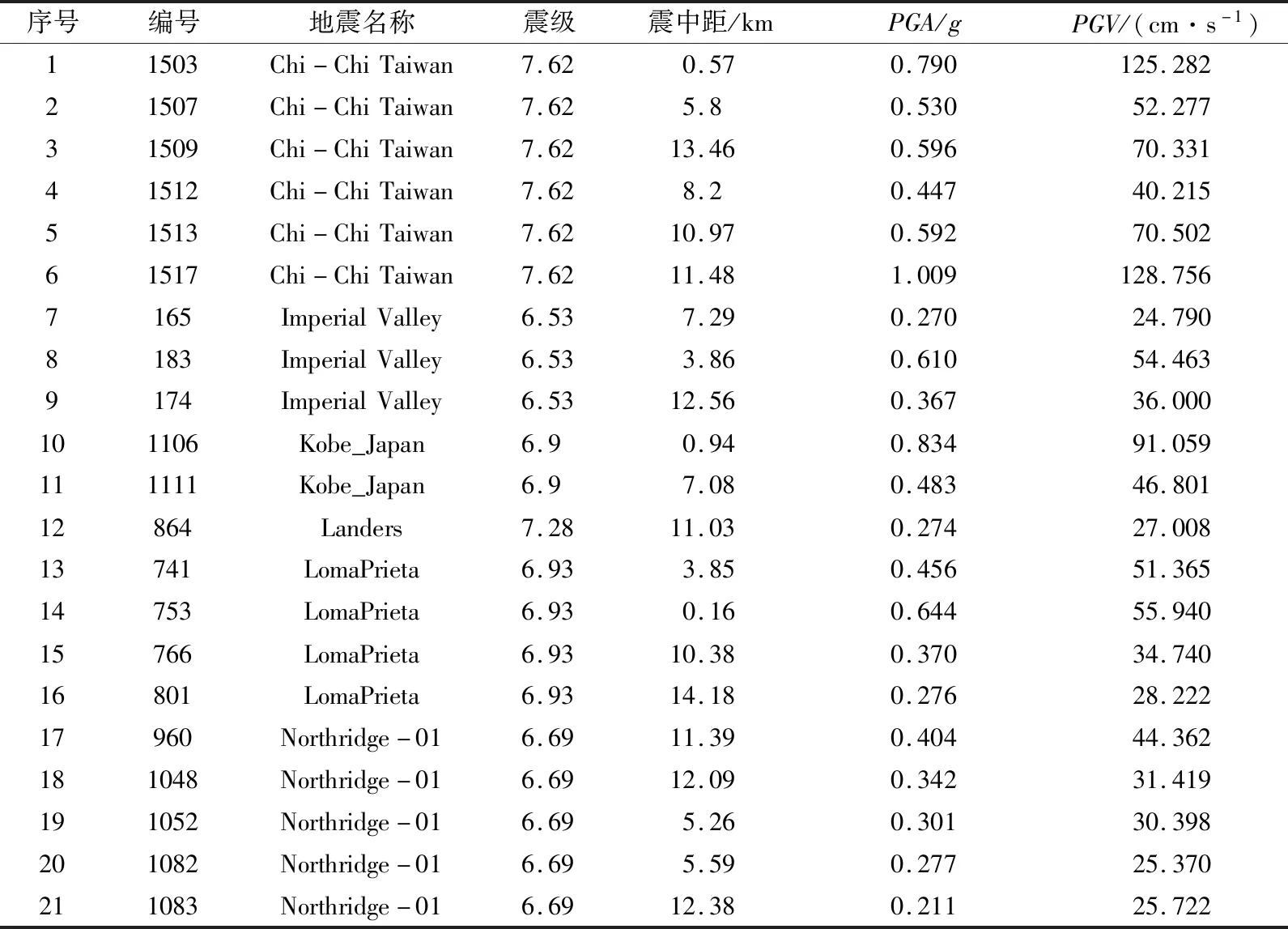
表4 用于增量动力分析的地震动Table 4 Ground motions for incremental dynamic analysis

4 地震易损性分析结果

4.1 可更换构件损伤模式

357条地震动下的IDA分析表明,可更换构件分级耗能机制显著,损伤演化规律如图6所示。

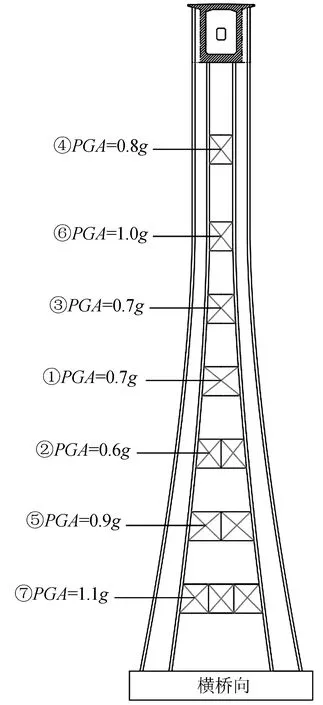
图6 可更换构件损伤机理Fig.6 Damage mechanism of replaceable members

参考文献[17],可更换构件中的弦杆采用钢材为Q345,其屈服应变为0.001 67,斜腹杆与竖杆采用钢材为Q235,其屈服应变为0.001 14。斜腹杆在PGA为0.5g时开始屈服,在PGA为1.1g时七排斜腹杆全部屈服,屈服顺序依次为第四、五、三、一、六、二、七排。在强震激励下不同类型可更换构件的地震响应不同,其中斜腹杆的地震响应远大于竖杆与弦杆,这是因为弦杆的地震应力主要由四根墩柱之间的相对位移引起,而在地震作用下墩柱间的相对位移较小,所以弦杆所受应力较小,而斜腹杆应力主要是由墩柱之间的剪力所致。

9度设计地震PGA为0.4g时,钢桁架杆件未发生屈服,墩柱处于基本完好状态;在9度罕遇地震PGA为0.64g时,钢桁架杆件中有两排斜腹杆屈服,钢桁架进入屈服耗能阶段,这时可更换构件开始吸收耗散地震能量,但墩柱仍基本完好。

4.2 IDA曲线

根据IDA分析基本步骤,分别得到可更换构件高墩墩底、墩中钢筋与混凝土材料应变的IDA曲线簇如图7所示。文中、图中及表中,墩中区域表示墩柱距墩底57.5～62.5 m之间。

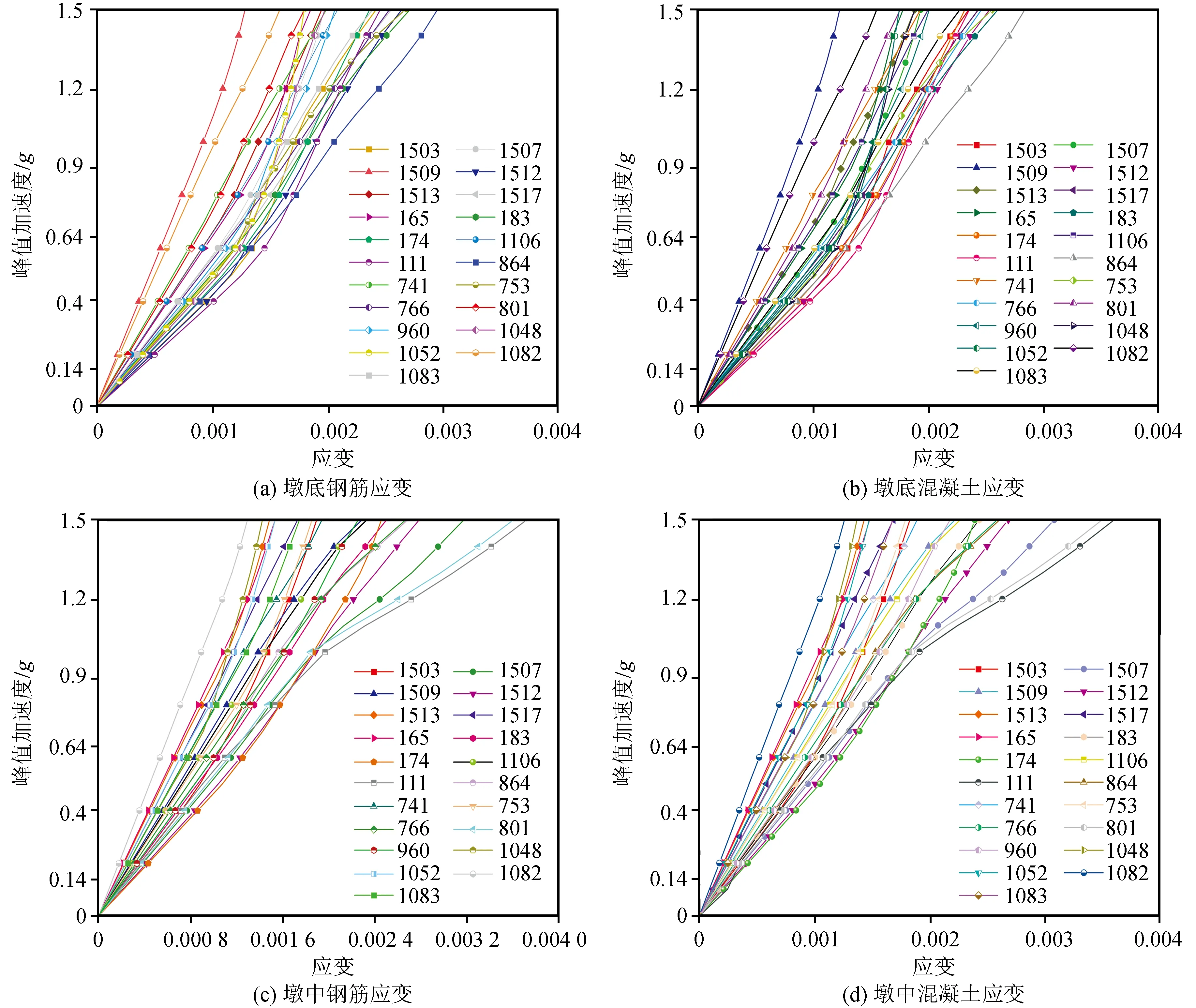
图7 IDA曲线Fig.7 IDA curves

由图7可知,单条IDA曲线基本呈线性变化,21条IDA曲线呈现出一定的离散性,弹性阶段时曲线簇离散性小,弹塑性阶段曲线簇的离散性明显增大。对比墩底与墩中的IDA曲线簇,墩中曲线簇离散性较大,说明在塑性阶段,墩中位置对强度变化较墩底更加敏感。

4.3 墩柱50%、84%及16%分位IDA曲线

对墩柱曲线簇进行数据处理得到概率分位IDA曲线如图8所示。其中50%分位曲线用于统计IDA分布离散数据的中心位置,度量多条IDA曲线的集中趋势,84%与16%分位曲线表示样本数据对中心位置的标准偏差,考察数据离散程度。

由于可恢复功能结构体系具有比传统抗震结构更高的抗震性能,现代抗震设计理念亟需从传统抗倒塌设防目标转向灾后可恢复功能目标,传统结构“小震不坏、中震可修、大震不倒”的抗震设防目标,无法体现出可恢复功能结构的优越性。因此,第五代《中国地震动区划图》提出了可恢复功能结构“小震及中震不坏,大震可更换、可修复,巨震不倒塌”的四水准抗震设防目标[18]。本文将9度巨震的PGA定义为1.2g,并对罕遇地震、极罕遇地震下墩柱的抗震性能进行了评价。

由图8可知,在9度设计地震PGA为0.4g时,墩底钢筋应变为0.000 73,混凝土应变为0.000 71,墩中的钢筋应变为0.000 61,混凝土应变为0.000 59,再结合表2可知,此时墩柱处于基本完好状态;在9度罕遇地震PGA为0.64g时,墩底钢筋应变为0.001 15,混凝土应变为0.001 11,墩中的钢筋应变为0.000 98,混凝土应变为0.000 95,此时墩柱仍处于基本完好阶段。在9度巨震PGA为1.2g时,墩底钢筋应变为0.001 83,混凝土应变为0.001 76,墩中的钢筋应变为0.001 77,混凝土应变为0.001 72,此时墩柱仍处于基本完好阶段。在PGA增大到1.35g时,墩底钢筋应变为0.002 11,墩底纵筋屈服,墩中钢筋应变为0.001 86,墩中钢筋未屈服,墩柱底部形成第一个塑性铰;当PGA继续增大到1.39g时,墩中钢筋应变为0.002 08,墩中纵筋屈服,墩柱中部区域形成第二个塑性铰。

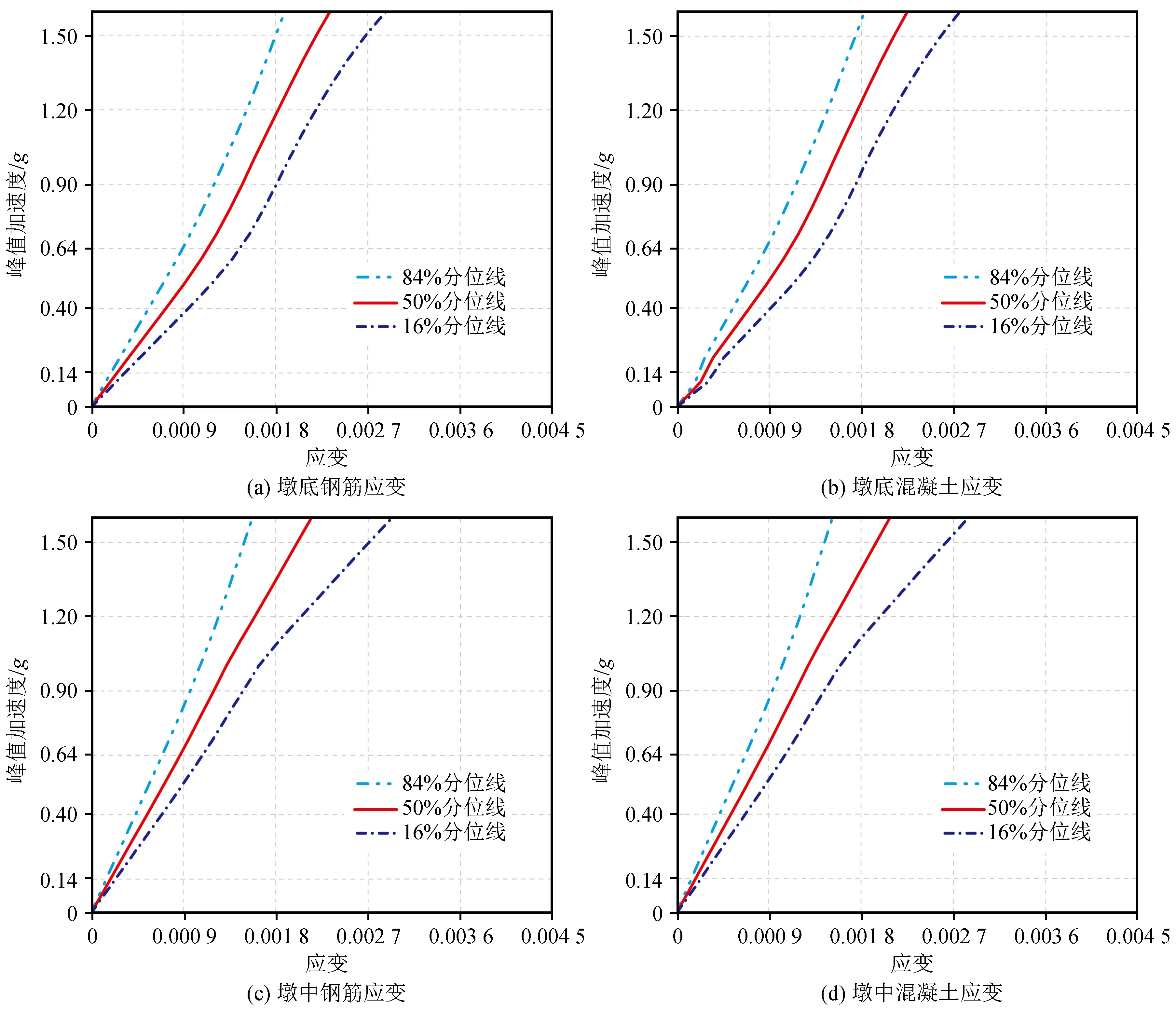
图8 50%、84%、16%分位IDA曲线Fig.8 IDA curves of 50%,84%,and 16% fractiles

4.4 地震易损性曲线

通过对IDA分析所得的离散数据进行二次回归分析,可得各个极限状态下拟合回归系数a、b、c,回归系数列于表5。将a、b、c代入式(2),即可得到结构各个极限状态下的能力需求比的拟合值。再将其代入式(1)即可绘制以PGA为横坐标的地震易损性曲线如图9所示。墩柱的损伤超越概率列于表6。

表5 回归系数Table 5 Regression coefficient

由图9、表6可知,在9度设计地震PGA为0.4g时,墩柱处于基本完好状态;在9度罕遇地震PGA为0.64g时,墩柱处于基本完好状态的概率为99.5%;在9度极罕遇地震PGA为1.2g时,墩柱处于基本完好的超越概率为36.6%,发生可修复性损伤的超越概率趋于0;当PGA继续增大到1.5g,墩柱基本完好状态超越概率为67.7%;发生可修复性损伤超越概率不足1%,发生严重损伤超越概率几乎为0。综上所述,在强震作用下,墩柱通常处于基本完好状态或可修复性状态,出现严重损伤状态的概率极低,究其原因,结构通过可更换构件的屈服,延长结构周期、吸收耗散地震能量,从而保护墩柱,使桥墩整体具有优越的抗震性能。

图9 地震易损性曲线Fig.9 Seismic fragility curves

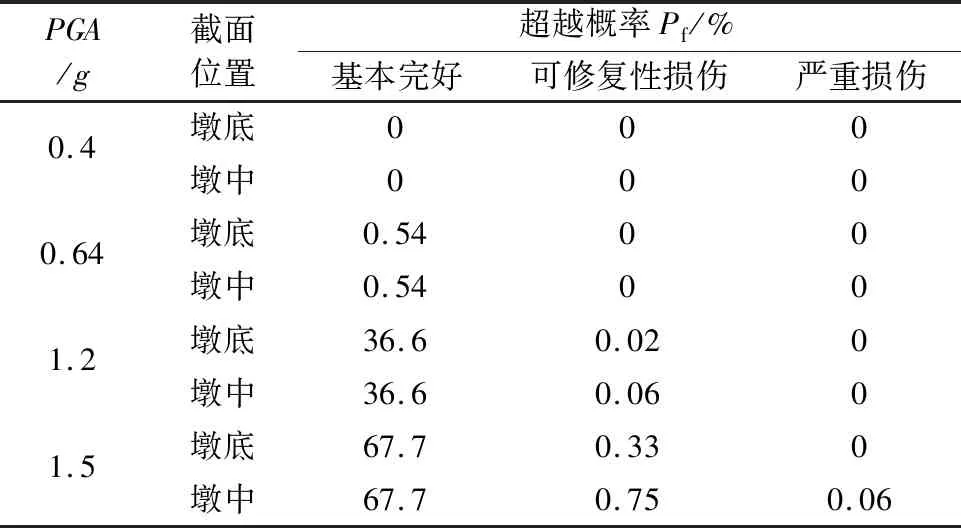
表6 墩柱的损伤超越概率Table 6 Exceedance probability of column damage

可更换杆件在9度罕遇地震下处于可修复性损伤的概率较大,在9度极罕遇地震作用下,大概率处于严重损伤状态。可更换杆件集中结构塑性损伤,达到预期的损伤控制效果。限于篇幅,分析结果不具体列出。

5 结论

(1) 新型铁路高墩中可更换构件损伤演化规律为中间第四排钢桁架最先开始屈服,然后向两端逐渐扩展。可更换构件在PGA约为0.5g时开始屈服,在1.1g左右时七排钢桁架全部屈服,分级耗能机制显著。

(2) 可更换构件新型高墩结构在9度罕遇地震PGA为0.64g时处于基本完好状态的概率为99.5%。

(3) 墩柱在PGA为1.35g时在墩底形成第一个塑性铰,在PGA为1.39g时在距墩底57.5～62.5 m之间的墩中区域形成第二个塑性铰。

(4) 可更换构件新型高墩结构在9度极罕遇地震下超越基本完好状态的概率为36.6%,超越可修复性损伤状态的概率不足1%,其大概率处于可修复性损伤状态,可更换构件桥墩具有优越的抗震性能,满足了四水准的抗震设防目标。