On the dimension of the divergence set of the Ostrovsky equation

Yajuan ZHAO(赵雅娟)+

Henan Academy of Big Data，Zhengzhou University，Zhengzhou 450001，China E-mail : zhaoyj-91@zzu.edu.cn

Yongsheng LI (李用声)

School of Mathematics，South China University of Technologg，Guangzhou 510640，China E-mail : gshli@scut.edu.cn

Wei YAN(闫威)Xiangqian YAN (闫向前)

School of Mathematics and Information Science,Henan Normal University，Xinaciang 453007,China E-mail: 011133@htu.edu.cn; yan.aiangqian213@126.com

1 Introduction

The Ostrovsky equation

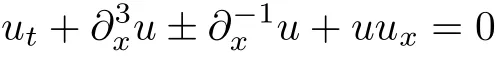
was proposed by Ostrovsky[12，19，26]as a model for weakly nonlinear long waves in a rotating liquid that take into account of the Coriolis force. The equation describes the propagation of surface waves in the ocean in a rotating frame of reference. Some researchers have investigated the Cauchy problem for the Ostrovsky equation;see[6，13–16，22，30，32，34]and the references therein.

2 Preliminaries

In this section， inspired by [28]， we give a crucial oscillatory integrals estimate related to the free Ostrovsky equation. First of all， we recall the following well-known variant of van der Corput’s Lemma:

Lemma 2.1 ([29] P. 332-334) For a ＜b and I =[a，b]， let Φ ∈C∞(I) be real-valued and let ψ ∈C∞(I). Then，

3 Demonstration of Theorem 1.1

3.1 Proof of Theorem 1.1(i)

3.2 Proof of Theorem 1.1(ii)

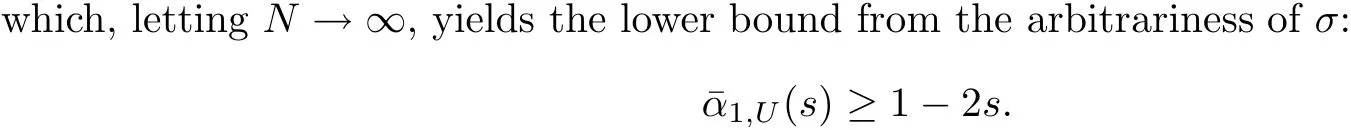
4 Appendix

In this section， we will give the proof of (1.4). First， we state and prove a Lemma which will be used to prove (1.4).