MAXIMAL L1-REGULARITY OF GENERATORS FOR BOUNDED ANALYTIC SEMIGROUPS IN BANACH SPACES*
Myong-Hwan RI
Institute of Mathematics, State Academy of Sciences, Pyongyang, DPR Korea
E-mail: math.inst@star-co.net.kp
Reinhard FARWIG
Department of Mathematics, Darmstadt University of Technology, Germany
E-mail: farwig@mathemtik.tu-darmstadt.de
Abstract In this paper, we prove that the generator of any bounded analytic semigroup in (θ,1)-type real interpolation of its domain and underlying Banach space has maximal L1-regularity, using a duality argument combined with the result of maximal continuous regularity. As an application, we consider maximal L1-regularity of the Dirichlet-Laplacian and the Stokes operator in inhomogeneous Bsq,1-type Besov spaces on domains of Rn, n ≥2.
Key words Maximal L1-regularity; sectorial operator; Stokes operator
1 Introduction
A central question for parabolic evolution equations in Banach spaces is whether a related linear operator will have maximal regularity. Maximal regularity of a closed linear operator can efficiently be applied to study related quasilinear and semilinear evolution equations; for relevant background material, we refer, for example, to [2, 14, 25]. In this paper, we study maximal L1-regularity of sectorial operators in Banach spaces. An advantage of maximal L1-regularity of sectorial operators is that for the Cauchy problem (1.1) with nonzero initial value u0the existence of strong solutions is guaranteed without requiring higher regularity on u0than required for the mild solution; this is not the case with maximal Lp-regularity for p ∈(1,∞). This property is efficient, for example, when considering density-dependent Navier-Stokes equations, cf. [12, 13].
Given a Cauchy problem
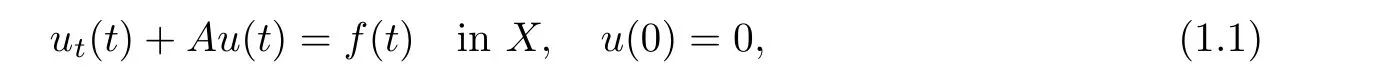
with a closed linear operator A in a complex Banach space X, the operator A is said to have maximal Lp-regularity in X for p ∈[1,∞], if for every f ∈Lp(R+;X), where R+= [0,∞),problem (1.1) has a unique solution satisfying

where BC(J,X) is the space of all X-valued bounded and continuous functions on J.
Let us recall some known results for maximal regularity. If a sectorial operator in a Banach space has maximal Lp-regularity for some p ∈(1,∞), then so does it for all p ∈(1,∞) (see[8, 16, 29]). Furthermore, (1.2) holds with temporally weighted space Lpγ(R+;X) with norm‖t1-γu‖Lp(R+;X)for all p ∈(1,∞), γ ∈(1/p,1], that is, maximal Lpγ-regularity,seeing [26]. If a densely defined closed linear operator A has maximal Lp-regularity for p ∈(1,∞) or maximal continuous regularity, then -A must generate an analytic semigroup in the underlying Banach space ([15, 16, 23]).
By a classical result ([28]), generators of bounded analytic semigroups in Hilbert spaces have maximal Lp-regularity for p ∈(1,∞). It was shown in[17,Theorem 3.2]that if a sectorial operator A in a UMD space X admits bounded imaginary powers (BIP) in L(X) with power angle less thanπ2, that is,‖Aiτ‖L(X)≤ceθ|τ|, τ ∈R,with some θ ∈(0,π2),then A has maximal Lp-regularity in X for p ∈(1,∞)(see also[10], [14,Theorem 4.4],and[2, Theorem III.4.10.7]).Note that UMD spaces are reflexive.
The operator A with-A being the generator of a bounded analytic semigroup in a Banach space E has maximal continuous and L∞γ(γ ∈(0,1])-regularity in the continuous interpolation space X = (E,E1)0θ,∞, θ ∈(0,1), where E1= D(A) is endowed with the graph norm of A; see [11, Th´eor`eme 3.1], [6, Theorem 2.14], [2, Theorem III.3.4.1] and [27, Theorem 3.5].We note that if A has maximal continuous regularity in a Banach space X, then X can be neither reflexive nor weakly sequentially complete ([9, Remark 2.4 (d)], [2, Remarks III.3.1.3(b)]). Moreover, if A is unbounded and has maximal L∞-regularity, then X must contain a complemented subspace isomorphic to c0([21]).
Concerning maximal L1-regularity,in [20], the property was proved for the negative Laplacian in FM(Rn), which is the Fourier image of the space of Radon measures on Rnwith finite total variation. It is shown that the Stokes operator has maximal L1-regularity in homogeneous Besov spaces ˙Bsp,1(Ω),p ∈(1,∞),s ∈(1/p-1,1/p),where Ω is the whole or half space,a smooth bounded or exterior domain (see [12, 13]). It is worth mentioning that in these papers,the proof is essentially based on properties of the heat kernel on Rn; moreover, in [12, 13] the Littlewood-Paley characterization of Besov spaces is crucial.
On the other hand, for a generator-A of an analytic semigroup,A does not have maximal L1-regularity if it is unbounded and the underlying Banach space does not contain a complemented subspace isomorphic to l1(see [21, Theorem 5]). Thus, it follows by [24, Theorem 2.e.7] that maximal L1-regularity does not hold in reflexive Banach spaces. It is known by [22,Theorem 3.6] that when -A is the generator of a bounded analytic semigroup in a Banach space X, maximal L1-regularity of A is equivalent to
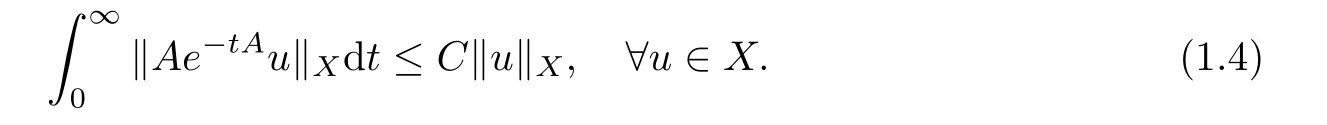
One can check that (1.4) holds when A is the generator of a bounded analytic semigroup in a Banach space E with 0 in its resolvent set ρ(A)and X =(E,E1)θ,1,θ ∈(0,1),where E1=D(A)is endowed with graph norm of A. However, it is not clear whether (1.4) can still be easily proved without the invertibility condition 0 ∈ρ(A). We note that maximal regularity without assuming 0 ∈ρ(A) allows the estimate constants for solutions to the Cauchy problems (1.1) on finite intervals to be independent of the lengths of the time interval, which is very important in the existence and stability theory for corresponding nonlinear problems.
In this paper,we show that maximal L1-regularity for the generator of any bounded analytic semigroup in(θ,1)-type real interpolation of Banach spaces can follow directly from the known maximal continuous regularity result by a duality argument without assuming 0 ∈ρ(A). We remark here that (L1(J,E))′= L∞(J,E′), assuming that E is reflexive or E′is separable,and (BC(J,E))′= M(J,E′), the space of all E′-valued BV measures, and hence the duality argument is not obvious at all.
Below,for Banach spaces E and E1,the notation E1E means that E1is continuously and densely embedded in E. The dual space of E is denoted by E′. Let L(E1,E)stand for the set of all linear bounded operators from E1to E, and let L(E)=L(E,E). Furthermore,Isom(E1,E)denotes the set of all norm isomorphisms from E1to E. The notation A ∈H(E1,E) means that A ∈L(E1,E)and, considered as an unbounded linear operator in E with D(A)=E1, -A generates an analytic C0-semigroup {e-tA}t≥0in E.
The main result of the paper is as follows:
Theorem 1.1(Maximal L1-regularity) Let E and E1be complex reflexive Banach spaces with E1E and let A ∈H(E1,E) be such that {e-tA}t≥0is a bounded analytic semigroup in E. Then, for θ ∈(0,1) the realization of A in Eθ,1:= (E,E1)θ,1has maximal L1-regularity in Eθ,1. More precisely, for f ∈L1(R+,Eθ,1), the Cauchy problem (1.1) with X = Eθ,1has a unique solution u such that ut, Au ∈L1(R+,Eθ,1) and
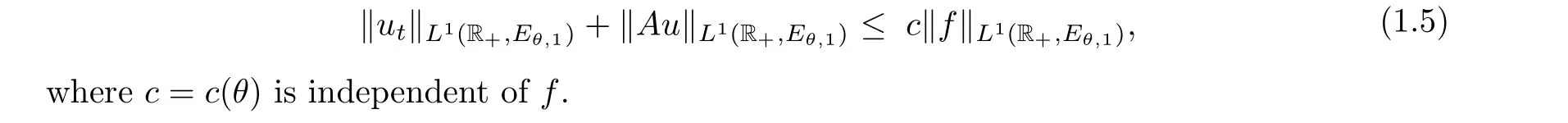
The main idea for the proof of Theorem 1.1 is to use a duality argument based on maximal continuous regularity for a backward-in-time problem in continuous interpolation spaces which are obtained by a method of extrapolation of E1and E introduced e.g. in [2, 3] (see also Subsection 2.1).
The following corollary is a direct consequence of Theorem 1.1:
Corollary 1.2 Under the same assumptions on the spaces E,E1and the sectorial operator A as in Theorem 1.1, let {(Eα,Aα) : α ∈R} be the interpolation and extrapolation scale generated by the real interpolation functor {(·,·)θ,1: θ ∈(0,1)} and (E,A) (see Subsection 2.1). Moreover,if α ∈Z, let
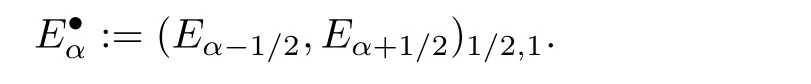
(i) If α ∈(k,k+1) with k ∈Z, then Aαhas maximal L1-regularity in Eα-1.
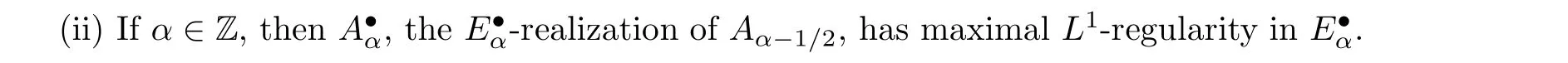

2 Preliminaries
2.1 Interpolation and extrapolation scales


2.2 Vector measures with bounded variation


3 Proof of the Main Result



4 Maximal L1-Regularity of Dirichlet-Laplacian and Stokes Operator in Besov Spaces Bsq,1

4.1 Dirichlet-Laplacian
Let Ω ⊂Rn,n ∈N, be a domain with uniform C2-boundary ∂Ω. The Dirichlet-Laplacian-ΔΩis defined by -ΔΩu:=-Δu for u in

Thus,Theorem 1.1 and Corollary 1.2 result in the following proposition where-ΔΩdenotes the Dirichlet-Laplacian extended or restricted to Bsq,1,0(Ω), s ∈(-2,2) (see (4.1)–(4.3)).


4.2 Stokes operator



 Acta Mathematica Scientia(English Series)2022年4期
Acta Mathematica Scientia(English Series)2022年4期
- Acta Mathematica Scientia(English Series)的其它文章
- ITERATIVE ALGORITHMS FOR SYSTEM OF VARIATIONAL INCLUSIONS IN HADAMARD MANIFOLDS*
- Time analyticity for the heat equation on gradient shrinking Ricci solitons
- The metric generalized inverse and its single-value selection in the pricing of contingent claims in an incomplete financial market
- The global combined quasi-neutral and zero-electron-mass limit of non-isentropic Euler-Poisson systems
- Some further results for holomorphic maps on parabolic Riemann surfaces
- Global well-posedness of the 2D Boussinesq equations with partial dissipation
