基于模糊层次分析法的石拱桥适用性评价分析
郝务宸,董友强,迟 宇,3,张 涛,邓 扬,侯妙乐,李爱群
1. 建筑遗产精细重构与健康监测重点实验室,北京 100044;
2. 北京建筑大学 土木与交通工程学院,北京 100044;
3. 北京市测绘设计研究院,北京 100038;
4. 北京市考古研究院,北京 100085
0 引 言
石拱桥,作为中国传统桥梁四大基本形式之一,遍布祖国山河大地,是中国古代灿烂文化中的重要组成部分,显示了中国古代人民的智慧和力量,具有极高的历史文化价值和科学价值,至今仍在交通基础建设中发挥着重要的作用。但是,随着时代的变迁,部分石拱桥受环境的侵蚀、荷载运营、人为破坏以及其他外界因素的影响,正遭受各种病害的侵扰,致使石拱桥状态发生变化,与最开始的设计或者竣工时的状态发生偏差,轻则缩短石拱桥的使用寿命,重则导致石拱桥整体坍塌,威胁着人们的财产安全[1-3]。因此对石拱桥进行适用性评价具有重要意义,能够从石拱桥的真实现状出发,判断主要结构及构件在正常的荷载作用和使用寿命期内能否正常使用,极其适用于仍在应用状态的石拱桥。
传统的古石拱桥适用性评价方法简单并且指标单一,仅仅利用主观的判断来确定评价体系指标的权重,从而缺乏客观性和可靠性。对于石拱桥的定性评价主要以专家的经验为主,因此评价结果主观性较强,存在不确定性。定量评价利用严格的数学公式对石拱桥进行评价,但是得到的结果很难用于保护工作中,因此评价结果具有一定的局限性。国内外许多专家对桥梁的评价方法进行了大量的研究,主要方法可分为5 种:加权平均法、荷载实验法、专家评价系统、模糊综合评价法、层次分析法[4]。LI Y D[5]通过建立荷载模型,实时分析桥梁构件的受力状态,并将其作为桥梁保护的主要依据。蒋田勇等[6]利用层次分析法对石拱桥进行评定并证明了该方法的科学性和可行性。鲍英基等[7]通过层次分析法构建桥梁评价体系,利用模糊综合判断法对实际案例进行分析讨论,实现对桥梁工程质量的定量评估。郑文魁[8]以厦深铁路流冲河特大桥为例,建立桥梁跨河施工方案评价体系,利用模糊决策理论建立数学模型,为桥梁跨河施工方案决策提供新的方法。郝记秀[9]利用模糊综合评价法构建了桥梁施工安全风险评价模型,对桥梁施工的安全状况进行了有效的评估。在充分了解上述研究之后,本文选取模糊层次分析法(Fuzzy Analytical Hierarchy Process,FAHP)对石拱桥进行适用性评价分析,得到石拱桥的适用性评价等级,为石拱桥的保护工作提供技术支撑。
模糊层次分析法是兼顾定性评价和定量评价的一种综合的适用性评价方法,能够将FAHP 中的模糊性和AHP 中的一致性有效地结合起来。该方法灵活、简洁、实用,在我国各个领域受到广泛的关注,但受主观性和不确定性的影响[10],构造的判断矩阵需要进行多次一致性检验,并且和专家的思维决策存在偏差,因此利用FAHP 构造模糊一致矩阵,无需进行多次的一致性检验也可以保证矩阵的一致性[11]。基于FAHP 的石拱桥适用性评价步骤如图1 所示,结合石拱桥的组成结构和主要病害,利用层次分析法确定评价指标层,利用标度法获得各层指标的相对权重,利用模糊数学中的隶属函数获得底层指标的隶属向量,逐级计算出各层的隶属向量,最后按照最大隶属原则来确定石拱桥的适用性评价等级[12-13]。
1 石拱桥适用性评价体系构建
石拱桥主要由上部结构、下部结构、桥面系3 部分组成,上部结构包括拱券和拱上结构,下部结构包括桥墩和桥台两部分,石拱桥的桥面系包括桥面铺装、栏板、望柱及装饰构件石狮。
古石拱桥适用性评价指标与正常使用的各种因素有关,这种因素主要是通过病害具体呈现出来,因此在构建石拱桥适用性评价体系时需要与病害进行关联。由于石拱桥的结构是多层级的,因此确定每个分层的指标因素对建立石拱桥适应性评价十分重要。本文设定石拱桥适用性评价为顶层指标,石拱桥上部结构、下部结构、桥面系为高层指标,拱券、拱上结构、桥墩、桥台等为中层指标,每个中层评价指标的病害情况作为底层指标,如图2 所示。顶层指标为A1,高层指标为B1-B3,中层指标为C1-C6,底层指标为D1-D14。
2 基于FAHP的石拱桥适用性评价
2.1 指标权重及一致性检验
由于石拱桥的组成结构和病害情况存在着模糊性,为了使石拱桥适用性评价对某些评价指标描述定量化,因此选用1 ~9 标度法来确定石拱桥各项指标之间的相对重要程度(表1)。

表1 1 ~9 标度值及其含义Tab.1 1-9 scale values and their meanings
通过比较选取的各项指标对石拱桥的影响程度来定义模糊判断矩阵A,其中判断矩阵A=(aij)n×n的一般形式为:

式中,定义W为石拱桥各因素的权重向量,其中Mi为判断矩阵A每行指标的乘积,利用归一化计算得到方根向量¯Wi,最后得到权重向量W并得出判断矩阵的最大特征值λmax,进行判断矩阵的一致性检验。CI为一致性指标,当只有两个元素时无需引入一致性指标,只需要判断λmax是否为2,如果为2 则证明判断矩阵符合一致性原则;当元素多于两个时,需要对判断矩阵进行一致性检验。CR为一致性比率,RI为平均随机一致性指标,RI随着判断矩阵维数的变化而变化[14](表2)。

表2 平均随机一致性指标(RI)取值Tab.2 Average random consistency index(RI)values
通常情况下,CR数值越小,判断矩阵的一致性越好,以此判断矩阵计算得到的权重向量W可以作为石拱桥每个因素的相对权重。当CR≤0.1 时,则判断矩阵满足一致性检验;如果CR>0.1,则说明判断矩阵不具有一致性,需要通过标度法重新对石拱桥的因素集赋予相应的权重系数,直到判断矩阵符合一致性检验。
2.2 模糊综合评价
2.2.1 评价等级及保护方案
由于石拱桥的适用性评价存在相应的模糊性问题,因此建立各项指标的评价集V={V1,V2,…Vn}用来表达每个因素的模糊向量,最后通过最大隶属度原则获得石拱桥的适用性评价等级[15]。根据我国现有的桥梁保护规范,将石拱桥的适用性评价集划分为5 个等级,V={V1,V2,…Vn}={优,良,中,差,劣}[16],各等级含义见表3。

表3 评价等级含义Tab.3 Definition of evaluation grade
2.2.2 模糊综合评价
石拱桥单因素模糊矩阵Ri是将石拱桥底层指标的隶属度组成模糊矩阵式(3)。如石拱桥拱上结构的单因素模糊矩阵是由侧墙、翼墙裂缝,砌筑材料风化两个指标的隶属度组成的,相同方法可以得到其他中层指标的单因素模糊矩阵。

石拱桥的一级模糊综合评价是以底层指标的单因素模糊矩阵为基础,从而得到中层指标的隶属向量。当底层指标各因素权重相同时,可以直接利用单因素模糊矩阵各行的隶属向量之和除以指标数量则可以直接得到中层指标的隶属向量[17],如果底层指标各因素权重不同则需要利用式(4)进行中层指标隶属向量的计算。

式中,B为中层指标的隶属向量;°为某种模糊运算符,为了能够考虑到所有因素的影响,并且能够保留单因素评价的所有信息[18],本文选取加权平均模型M(●,+)。
同理石拱桥的二级模糊综合评价是以中层指标的单因素模糊矩阵为基础来计算高层指标的隶属向量,通过计算也可以得出三级模糊综合评价结果,也就是顶层指标的隶属向量。最后按照最大隶属原则得到石拱桥适用性评价等级。
3 应用实例
3.1 拱券指标层权重系数计算
为了验证方法的可靠性,本文以北京卢沟桥为例,进行适用性评价分析。首先需要计算卢沟桥各层指标权重。以卢沟桥6 号拱券为例,利用1 ~9 标度法来比较拱券指标层中任意两个指标之间的相对重要性,列出卢沟桥拱券的判断矩阵(表4)。

表4 6 号拱券判断矩阵C1 及一致性检验结果Tab.4 No.6 arch judgment matrix C1 and consistency test results
3.2 隶属向量计算
通过对卢沟桥进行变形监测分析[19]得到卢沟桥拱券上游与下游的净矢高,净跨径之比作为计算拱轴线下绕和拱轴线相对形变的指数值,结合卢沟桥6 号拱券现场拍照和测量计算得到的拱券拱石脱落与拱腹裂缝指数值,利用隶属度函数,建立卢沟桥6 号拱券的单因素模糊矩阵,得到等级评分(表5)。图3a 为卢沟桥6 号拱券拱腹裂缝的修补情况,图3b 为拱石脱落修补情况。

图3 6 号拱券病害Fig.3 No.6 arch disease
利用公式(4)可以得出卢沟桥6 号拱券的隶属向量:[0.2082 0.2000 0.3863 0.1571 0.0484],根据表5 可以得出卢沟桥6 号拱券的单因素模糊矩阵如下:


表5 定量评价指标层数值及等级评价Tab.5 Quantitative evaluation index layer value and grade evaluation
3.3 结果分析
按照卢沟桥6 号拱券权重的计算步骤,计算得出卢沟桥各层指标的指标权重(表6)。

表6 卢沟桥指标层权重Tab.6 Weight of index layer of Lugou Bridge
得出卢沟桥各层指标权重之后,根据上一小节的具体步骤可以依次得出卢沟桥各层指标的一级、二级、三级模糊评价结果(表7)。
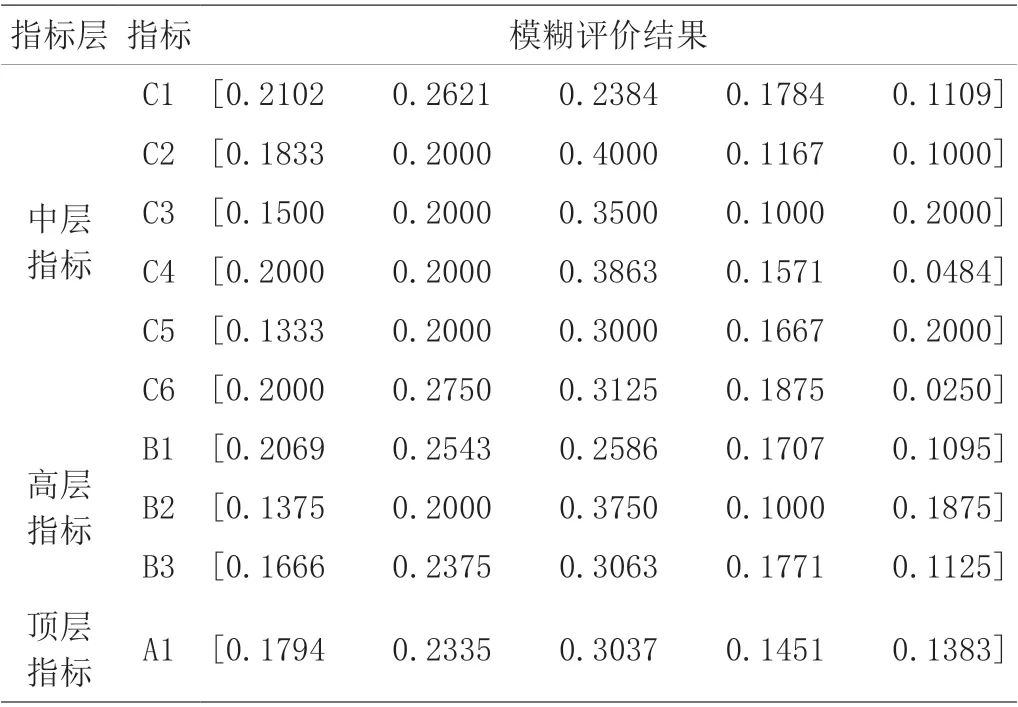
表7 卢沟桥各指标层模糊评价结果Tab.7 Fuzzy evaluation results of each index layer of Lugou Bridge
根据最大隶属度原则得知,卢沟桥的适用性评价等级为中级。以实际情况来看,卢沟桥目前已不再承担机动车的交通功能,所有机动车在旁边的卢沟新桥和京石高速公路上行驶,且卢沟桥历史文物修复委员会制定了保护方案,对卢沟桥进行定期维修保养。
4 结 论
针对石拱桥的适用性评价研究,本文提出了一种基于模糊层次分析法的适用性评价方法,通过对石拱桥的组成结构以及桥体的各类病害进行分析,建立石拱桥适用性评价体系,计算各指标层权重及隶属向量,最后通过最大隶属原则判断石拱桥的适用性评价等级。利用该方法对北京卢沟桥进行适用性评价分析,适用性评价等级为中级,符合卢沟桥的实际情况,验证了该方法的可靠性,并且可以为以后石拱桥的保护工作提供依据。但还存在着不足,本文的方法只对卢沟桥进行适用性评价,数据量较少,后续工作应增加其他石拱桥数据,进一步验证该方法的可行性。

