土工格室加固风积沙地基模型试验研究

王艳坤，刘 杰，宋 玲，张兴疆，高 斌

(1.石河子大学 水利建筑工程学院, 新疆 石河子 832003;2.新疆交通规划勘察设计研究院有限公司, 新疆 乌鲁木齐 830006)

0 引言

风积沙作为承载力较低的地基土，如不加固使用，会直接影响建筑物整体性和稳定性。采用土工合成材料对风积沙地基加固是改善地基性能的一种有效措施。土工合成材料被广泛应用在公路、铁路行业增强路基的稳定性，但土工格室加固机理至今研究并不深入。为了探究土工合成材料对地基的加固效果，国内外学者主要通过现场试验、模型试验、数值模拟并结合理论分析手段进行研究分析。在模型试验方面，李驰[1]利用模型试验对土工格栅在不同加筋方式下承载力的变化进行了分析。柏蕾[2]通过大型模型试验分析了不同尺寸方形加载板下加固地基的承载力、地基土压力的分布和土工格栅的应变。郑超毅[3]针对砂地基进行模型试验和Winkler弹性地基计算法共同分析，将试验值与计算值作对比，研究土工格室对地基承载力的影响。韩晓[4]利用模型试验，研究了不同地基压实度、不同格室焊距及不同格室埋深情况下的p-s曲线，土压力及格室应变的规律。侯娟[5]对不同类型的地基做了大量的模型试验，通过对比水平加固与横-竖加固的p-s曲线，分析了加固层数及布筋位置对地基承载力的影响。Mhaiskar[6]基于模型试验对格室参数、材料强度及填料参数等进行了承载力分析，从而鉴定了加筋效果。桩基承载力特性模型试验[7-8]主要通过研究荷载-位移曲线，不同桩长、坡度等方面，同样还利用实际工程与模型试验相互对比验证。现有的研究主要集中在地基加固方式、材料参数的研究，缺少对加固地基基础形状以及换填厚度的影响作用分析。

利用模型试验对土工格室不同埋深、不同土工格室加固层数、不同加载板形状及换填不同砾类土下的地基沉降量、应力分布、位移大小及格室应变进行研究，并对加固效果进行对比分析；探究土工格室加固风积沙地基的合理结构形式，并为沙漠工程提供一定的理论价值。

1 室内模型试验方案

1.1 试验装置

试验模型箱选取尺寸为250 cm×150 cm×150 cm(长×宽×高)大模型箱，并在模型箱边壁涂抹润滑油，铺设光滑薄膜，从而减小边界效应，测试电线采用蛇形布置减小对地基土的影响。模型箱外侧进行了加固，避免试验过程中模型箱变形，影响试验的准确性。

通过4块加载板叠合的方式来模拟基础，上面3块是正方形加载板，主要负责荷载均匀传递，下面一块分别采用3种相同面积不同形状的加载板进行加载，如表1所示。

表1 加载板尺寸

试验选用分离式油压千斤顶(100 kN)，并在其下方接传感器(1 000 kN)，利用超高压电动油泵传递施压。采用位移计(0～80 mm)测地基沉降，土压力盒采集竖向土压力，应变片采集土工格室的形变量。利用DH3816N应变采集箱连接所有设备，并通过计算机输出所有测量数据，试验装置如图1所示，格室及测量设备布置图如图2所示。

图1 试验装置

图2 格室及测量设备布置(单位:cm)

1.2 试验材料

室内试验采用的土工格室由聚乙烯条带按照一定焊距在焊缝处由超声波焊接而成，格室高度为3 cm，焊距10 cm，抗拉强度≥15 MPa。试验模拟的是格室满铺状态，土工格室的展开长度为120 cm，为模型箱长度的0.5倍；宽度为100 cm，为模型箱宽度的0.66倍。

试验所用的地基填料为风积沙和砂砾，取自s21阿克苏-乌鲁木齐高速公路103团服务区施工段，取样深度为2 m。风积沙和砂砾分别做筛分试验确定其颗粒级配参数如表2和表3所示。通过室内土工试验得到风积沙的重度为16 kN/m3，含水量为0.12%；砂砾的重度为18.2 kN/m3，含水量为6.3%。

表2 风积沙颗粒级配

表3 砂砾颗粒级配

1.3 试验方案

模型试验主要研究在竖向荷载作用下土工格室加固风积沙地基的受力及变形情况，并针对土工格室不同埋深、不同土工格室加固层数、不同加载板形状及换填不同厚度砾类土，设计了15组不同工况，如表4所示。

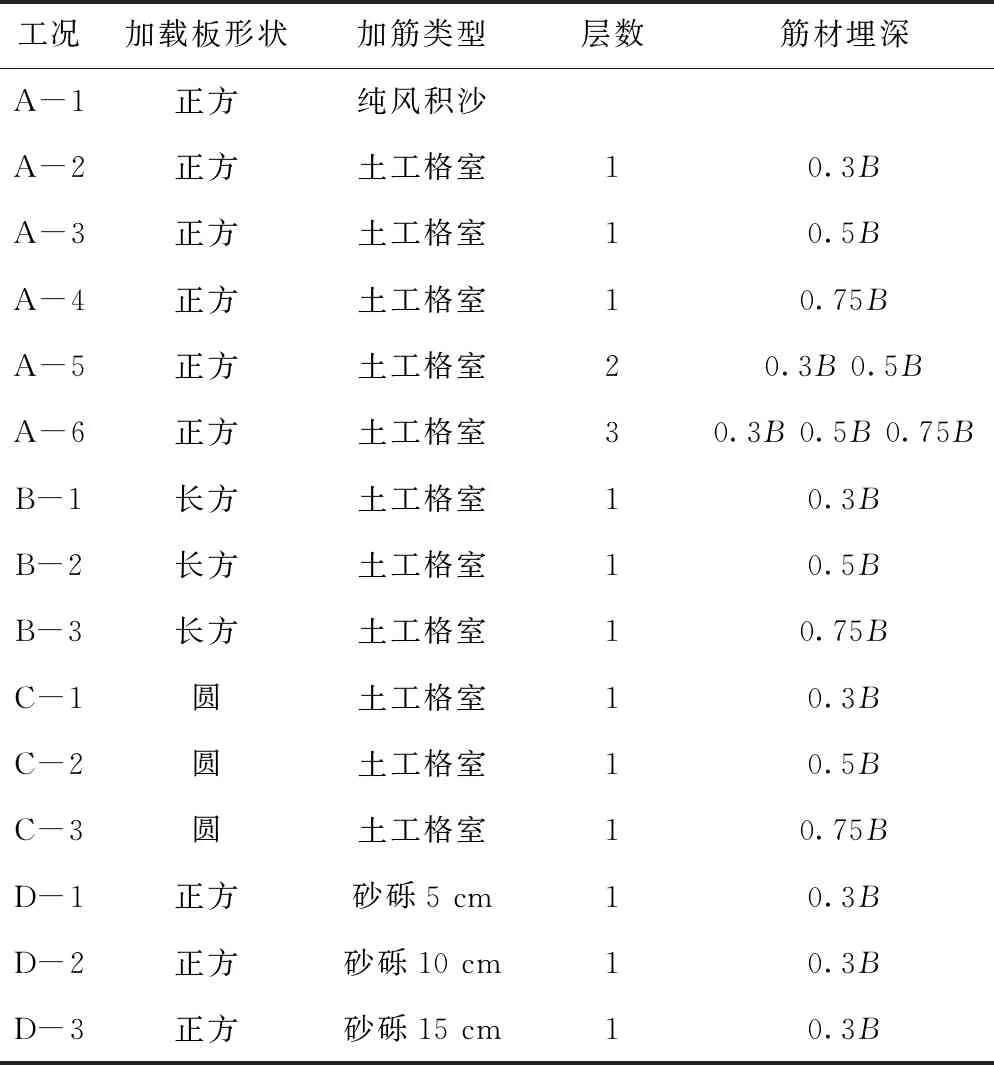
表4 试验工况

A-1为纯风积沙地基，A-2～C-3为土工格室加固的地基，主要研究筋材不同埋设方式和加载板形状对加固地基承载力的影响，D-1～D-3分别为采用相同埋深，5，10，15 cm这3种不同厚度的砂砾垫层加固地基，主要研究土工格室加固地基的等效当量砂砾换填厚度。

选取土工格室埋深为0.3B，0.5B，0.75B(B为正加载板宽度30 cm)，格室铺设层数N为1～3层。

风积沙采用砂雨法填筑的方法，地基压实度控制在95%。每30 cm取3个样做环刀试验，测量其压实度是否符合要求。为保证应变片准确测量土工格室拉伸变形，在铺设土工格室的过程中将每个网格完全撑开，如图3所示。然后将每个格室单元内填等量的土夯实，保证其压实度与整体一致。将地基填至1.2 m厚，预压之后，可以进行位移计、加载板的布置。将所有仪器布设好后，连接采集箱，进行调试，确认无误后开始加载。

图3 格室铺设

模型试验破坏标准为：当竖向荷载趋于稳定时，地基沉降量不断增大，即承载力出现了峰值。如果没有明显的峰值时，参考《建筑地基基础设计规范》(GB50007—2011)[9]中规定的地基变形允许值，本试验终止标准是沉降量超过60 mm即停止加载。

2 试验结果及分析

2.1 不同工况下风积沙地基荷载-沉降(p-s)曲线

根据试验结果，绘制纯风积沙与不同埋深(0.3B，0.5B，0.75B)时圆形、正方形与长方形加载板下风积沙地基的p-s曲线如图4所示。

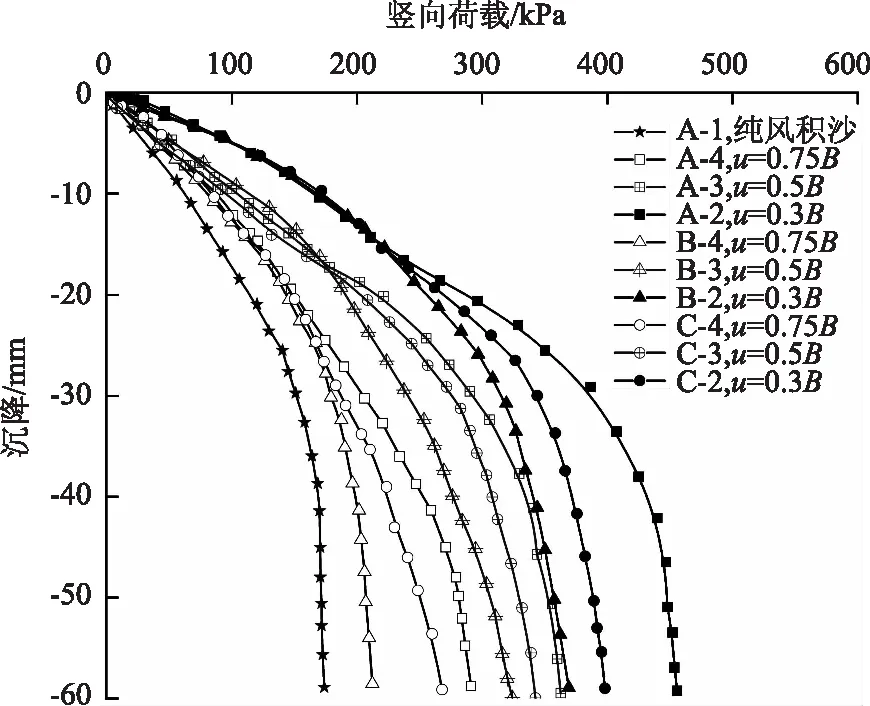
图4 不同埋深时不同形状加载板下的p-s曲线

由图4可以看出，土工格室加固风积沙地基在竖向荷载的作用下，破坏可分为以下几个过程。加压初始，风积沙地基为压密阶段，所有p-s曲线都接近直线，这是由于土的压密变形引起的地基沉降，竖直荷载较小，土工格室侧向约束作用未完全发挥。这一阶段土工格室埋深相同时，不同加载板形状下的p-s曲线非常接近且产生交点，这说明在地基压密阶段，加载板形状对地基承载力影响不大。加载中期，地基基础处于剪切阶段，p-s曲线不再呈直线，随着竖向荷载增大，加固风积沙地基的加固效果明显，不仅改变了地基破坏形式同时有效增大了地基承载力，减小了地基沉降量。加固后期，地基处于破坏阶段，p-s曲线再次出现变化，随着竖向荷载增大，加固风积沙地基沉降急剧增大，地基逐渐失稳，加载板周围出现较多裂缝，表面风积沙地基出现了整体剪切破坏。

由图4还可以看出，在土工格室加固风积沙地基中，相同形状的加载板加压时，随着格室埋深的增加，加固风积沙地基的承载力降低，埋深为0.3B时的加固效果最明显，与Fakher等[10-11]研究的结论相符。当埋深相同时，相同面积不同形状的加载板也有差别，正方形加载板的承载力最大，圆形和长方形较小[12]。当方形加载板加压时，正方形加载板能使边界应力均匀分布，地基周围受压均匀，而长方形短边则承受较大的应力，更易发生破坏；圆形加载板更利于应力向地基周围扩散，尺寸效应较大。因此，正方形基础相比于其他形状基础能更有效提升地基承载力。

以正方形加载板为例，加固层数对地基承载力的影响如图5所示的p-s曲线。加载初始，加固风积沙地基的曲线相差不大，这说明只有首层土工格室发挥作用，竖向荷载还未传递。加载中后期，多层格室带开始发挥作用，随着竖向荷载的增加，格室层数越多，其抵抗荷载的能力就越强。

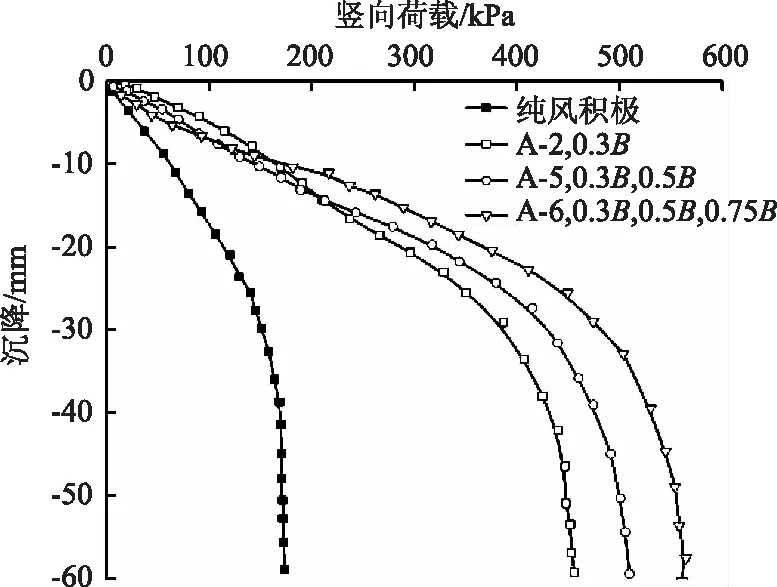
图5 不同加固层数的p-s曲线

由表5可以看出，在正方形加载板下，格室能够明显提高地基承载力。当格室层数为1层时，承载力提高为纯风积沙的2.62倍，2层时2.93倍，3层可达3.22倍。这表明在一定范围内，随着竖向荷载的增大，土工格室加固层数越多，地基承载力越高[13]，为沙漠工程中提高地基承载力提供了合理的加固布设需求。

表5 不同加固层数的承载力比较

2.2 地基土压力分析

在距离地表30，60，90 cm处分别埋设土压力盒，以正方形加载板为例，探究不同工况下的加固风积沙地基的同一位置竖直土压力的变化规律。

图6为在竖向荷载为455 kPa时，距离地表30 cm 处不同位置的竖向土压力变化图。由图6可以看出，在相同荷载条件下，A-2～A-6相较于纯风积沙地基附加土压力分别减少了33.43%，38.23%，46.58%，77.62%，87.25%。单层加固的地基中心位置的土压力值减小，而两侧土压力值却有增大趋势。从整体来看，在破坏状态时，格室埋深浅的承载力较强，格室受到的破坏越严重，变形也越大，土压力也越大。这是由于土工格室限制了土体的侧向约束，并将加载板上传递下来的竖向荷载分散到格室下层，使地基下部范围共同承担格室上层的竖向荷载，从而扩散地基中部土体所受的应力，减小了加载板下部应力集中现象。多层加固地基中心位置的土压力降低更明显，两侧分担的土压力也较小。这说明通过增加加固层数，可以更有效地减小竖向荷载的传递。当首层格室变形后，第2层格室可以在首层传递的竖向荷载上继续发挥约束作用，使土压力逐层递减。因此，在工程中可以通过增加格室层数来减少地基形变，提高地基承载力。

图6 距离地表30 cm处不同位置土压力变化

以方形加载板下单层土工格室筋材埋深0.3B的工况为例，进一步研究地基应力场的变化，绘出距离地表30，60，90 cm处竖向荷载为455 kPa时的土压力的变化图，以及在竖向荷载10～60 kPa 的位移变化图，如图7所示。

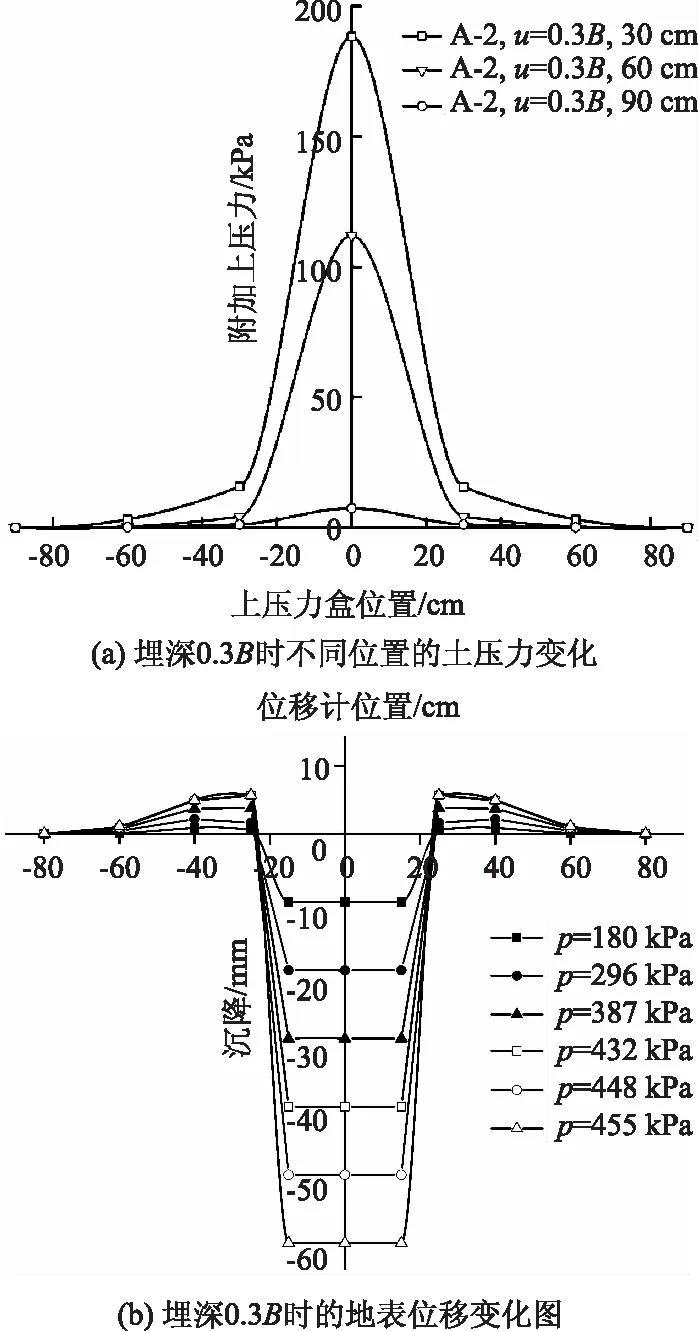
图7 埋深0.3B时不同位置的土压力及位移变化

由图7(a)可知，距地表30 cm处的土压力盒中心位置的土压力有188 kPa，60 cm时112 kPa，90 cm 时仅有7 kPa。可以看出，随着土压力盒埋深增加，土压力显著减小，且离基底越远，应力扩散效果越明显。这说明土工格室与土体形成了较大刚度的复合结构，起到了减小竖向压力、约束水平位移的作用，使竖向荷载传递范围更广，土压力在应力场内分布更均匀，从而改善地基承载力。

图7(b)是土工格室埋深0.3B时，正方形加载板受到压力传感器均匀的竖向荷载对应的不同地表位移图。随着竖向荷载增大，加载板下出现一个正方形沉降，正方形加载板周围土体则出现了裂缝和土体隆起。当加载板沉降由0～40 cm时，周围土体表面不断隆起，当超过40 cm时，周围土体表面不再发生隆起。结合图4，同样可以验证加载板沉降约在40 cm时出现极限地基承载力。这说明土工格室加固层造成的周围土体表面隆起，有效地扩散了应力，减缓了加载板上的应力集中现象。土工格室破坏后，加载板所受应力更多地传递到正下方，土工格室的侧向约束作用逐渐失效。

2.3 格室应变分析

为了研究土工格室应变的变化规律，以正方形加载板为例，选取如图2(b)所示不同位置的应变片，单层格室埋深0.3B时，格室拉应变随竖向荷载的变化如图8所示。

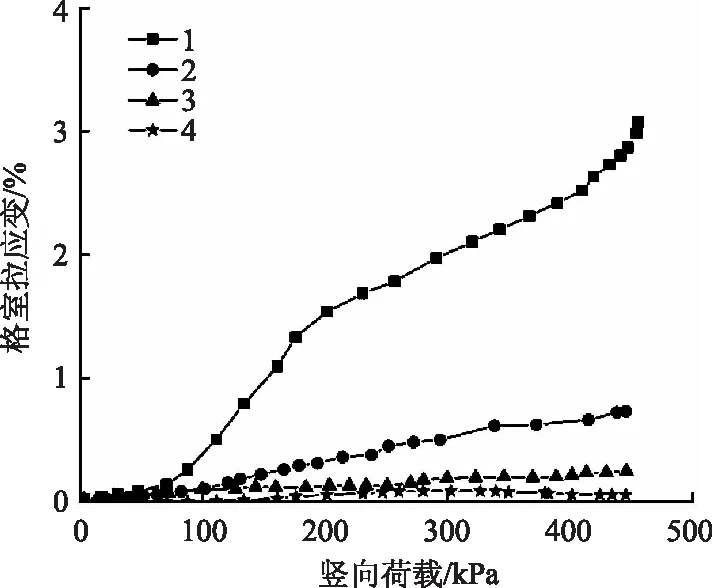
图8 埋深0.3B时格室拉应变随竖向荷载的变化

由图8可知，随着竖向荷载的不断增大，格室拉应变也增大，当竖向荷载达到80 kPa时，曲线的斜率发生变化，越靠近中心位置的格室斜率越大，中间格室的拉应变约为两侧的2倍，说明格室和土体之间发生了摩阻作用，且格室受力不均匀。

图9是单层格室在不同埋深情况下格室拉应变随位置的变化图，在方形加载板竖向荷载455 kPa的作用下，格室变形不均匀，加载板下方的变形明显大于两侧，且向两侧递减。随着格室的埋深增大，格室的拉应变减小，且变形相对均匀。其中埋深0.5B和0.75B加载板下格室拉应变较0.3B分别减少了0.92%,1.59%。这进一步说明格室的埋深不同对地基应力场的作用也不同，在一定情况下，格室埋深越浅受力越不均匀，越容易发生破坏。因此，在实际工程中，可选用较高强度的土工格室使用在埋深较浅的位置，能更有效地提高地基承载力。

图9 不同埋深格室拉应变随位置的变化

如图10和图11所示，不同加固层数的格室在不同位置的格室拉应变同样由中心向两侧递减。与单层加固格室相比，多层加固格室可以承受的竖向荷载更大，格室拉应变也就更大。在同一工况下，随着竖向荷载的增大，埋深越深的土工格室拉应变越小，其中两层格室埋深0.5B加载板下格室拉应变较0.3B减少了0.79%；3层格室埋深0.5B较0.3B减少了1.46%，埋深0.75B较0.5B减少了1.82%。这与土压力的变化正好一致，说明地基下部的应力是逐渐递减的过程。选用多层加固的方式加固地基，对埋深较深的格室可选用强度较低的格室加固，以减少工程造价，合理分配资源。

图10 两层格室拉应变随位置的变化

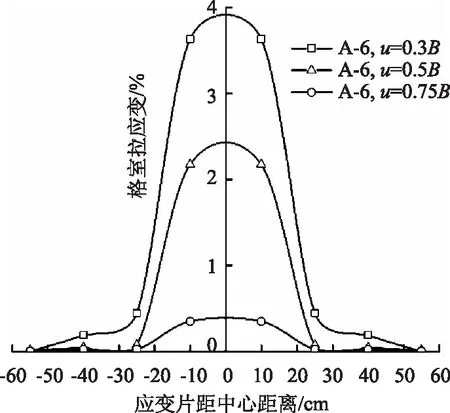
图11 三层格室拉应变随位置的变化

2.4 换填厚度分析

由图12可以看出，当换填砂砾厚度为5,10,15 cm时，相对于纯风积沙而言地基承载力分别提高了42.65%，48.90%，55.29%。纯风积沙地基本身能够承受的竖向荷载较小，但通过换填砂砾，可以有效提高地基承载力，而换填厚度的增加对提高承载力的效果并不显著。这是由于风积沙非常松散，黏聚力几乎为0[14]，受到外部荷载时很容易发生剪切破坏。但风积沙本身是有一定强度，通过换填砂砾对整体结构产生一个约束作用，增加了土的整体性；砂砾的强度是有限的，增加砂砾的换填厚度并不能大幅度提高地基承载力，砂砾阻止了基础快速刺入风积沙地基中，延缓了冲剪破坏的产生，地基承载力主要由砂砾下部的风积沙本身的承载力决定。

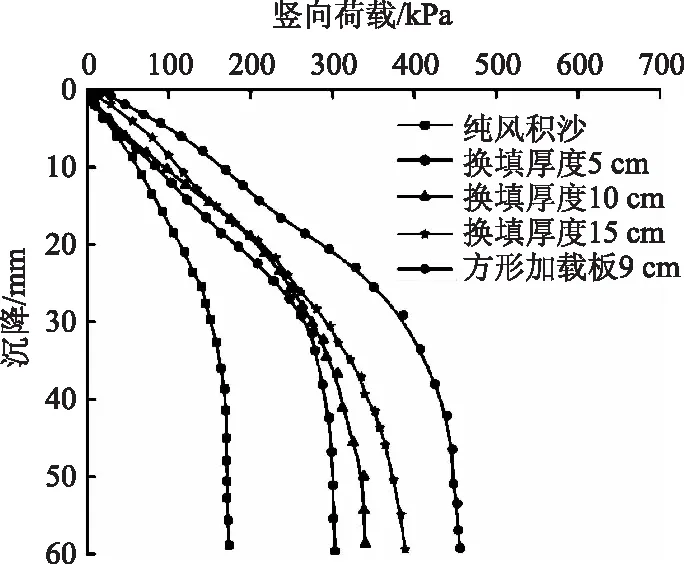
图12 不同换填厚度的p-s曲线

从图12中还可以看出，土工格室的加固效果比换填砂砾效果好，这是因为土工格室的侧限作用，提高了风积沙的整体性。因此，对风积沙进行侧限约束作用是处理风积沙地基的有效手段。

加固地基的地基承载力计算公式是在不加固地基承载力公式的基础上，考虑加固效果，修正得来[15]。为了研究公式在加固风积沙地基中的适用性，更清晰地表达土工格室加固与砂砾换填的等效关系，选取太沙基公式、换填垫层计算公式进行理论分析，并与试验进行对比。

对于方形基础，太沙基公式为：

pu=0.4bγNγ+1.2cNc+γdNq,

(1)

式中,pu为风积沙地基承载力；b为基础宽度；γ为风积沙土体重度；c为风积沙的黏聚力；d为加载板埋深；Nγ，Nc，Nq为承载力系数。

由式(1)计算出不加固地基的地基承载力为178.87 kPa(c=0，d=0，γ=16 kN/m3，Nγ=93.16)当用单层筋材加固时，在原有公式中加入其他作用的影响，因此增加的地基承载力值为：

(2)

修正的太沙基公式：

p′u=pu+Δp，

(3)

式中,T为土工格室的拉力之和;pu为极限承载力;s为最终的沉降量;r为地基两侧隆起圆的半径;β为土工格室拉力与水平面夹角(°)，其他意义同前。

计算可得增加的地基承载力值为291.22 kPa，加固后的地基承载力值为470.09 kPa，计算值与试验值误差为3%。

根据规范[16]规定换填土的承载力应符合：

pz+pcz≤faz，

(4)

式中，pz为垫层底面处的附加压力值；pcz为垫层底面处土的自重压力值；faz为垫层底面处深度修正后的地基承载力特征值。

矩形基础的垫层底面处附加压力值为：

(5)

式中,pk为加载板底面处的平均压力值；pc为加载板底面处土的自重压力值；z为加载板底面下垫层的厚度；θ为风积沙地基垫层的压力扩散角。

正方形加载板施压时b=l，计算结果如图13所示。由图可知，换填土公式计算值相较于试验实测值偏小，因此根据试验实测值对公式进行修正，适用于风积沙地基土工格室当量换填砾类土的理论表达式：

图13 计算值与实测值对比

(6)

(7)

式中,fu为风积沙地基承载力；k修正为换填土地基的修正系数；fai为试验实测换填土地基承载力；fbi为换填土公式计算的地基承载力；其他意义同前。

通过修正公式可以计算出相同位置1层土工格室可以等效22.3 cm厚的换填砂砾，与试验结果较为一致，说明提出的修正公式对该试验有较好的适用性，能较准确地反映出风积沙地基承载力值[17-20]。可为今后风积沙加固地基工程提供可靠依据。

3 结论

(1)通过比较不同加载板形状、不同格室埋深及不同加固层数工况下的地基承载力，发现利用正方形加载板施压的承载力高于同面积的圆形和长方形；单层加固格室埋深为0.3倍基础宽度时加固效果最好；增加格室层数能够使地基承载力提高2～4倍。

(2)土工格室加固风积沙地基距离基底越远，应力扩散效果越明显，所有工况地基中间所受土压力大于两侧，单层格室比多层格室加固应力集中现象更明显，单层加固中间格室土压力约降低1.5～1.8倍，多层加固降低约4.5～7.8倍；土工格室破坏后，格室的侧向约束作用逐渐失效，加载板土体周围的位移变化量减小。

(3)随着荷载增大加载板下格室的拉应变远大于两侧，单层格室加固时，格室埋深越浅受力越不均匀，越容易发生破坏，相同荷载下埋深大的较小的加载板下格室拉应变可减少约0.9%～1.6%；多层格室加固时，下层的土工格室受力更小，同一工况下层的较上层的加载板下格室拉应变可减少约0.7%～1.9%。

(4)对风积沙进行侧限约束作用是处理风积沙地基的有效手段；采用太沙基公式对土工格室加固风积沙地基进行承载力计算，计算值相较于试验实测值误差较小，能较准确表示风积沙地基承载力值，在试验基础上对换填土公式进行修正，得出土工格室加固风积沙的砾类土当量换填厚度。