一种基于神经网络的燃烧模型及其先验性检验

刘润之，罗 坤，邢江宽，樊建人

一种基于神经网络的燃烧模型及其先验性检验

刘润之，罗 坤，邢江宽，樊建人

(浙江大学能源工程学院，杭州 310027)

本研究采用神经网络方法，对准确的化学反应速率与反应标量之间的非线性关系进行建模，发展了一种基于人工神经网络(ANN)的燃烧模型．借鉴动态二阶矩模型建模思想，将标量分布的梯度纳入神经网络模型的输入集中，进一步发展出梯度输入人工神经网络(ANN-G)模型．基于一个预混火焰直接数值模拟数据库，对人工神经网络模型进行先验性研究，发现对于反应区域较薄的反应步，ANN模型与ANN-G模型都能准确计算化学反应速率．在泛化验证中，ANN-G模型比ANN模型表现更好．

湍流燃烧；人工神经网络；燃烧模型；先验性检验

湍流燃烧广泛存在于各类燃烧应用装置中，是燃烧研究中的基础现象之一，但由于湍流流动的多尺度特征、燃烧化学反应的非线性特征以及湍流流动与燃烧反应的强烈耦合，时至今日，湍流燃烧相互影响的机理的研究仍未完全揭示．目前的实验测量技术还难以准确解析出详细的多尺度的湍流燃烧现象，因此数值模拟计算在研究湍流燃烧机理上具有一定优势．湍流燃烧数值模拟主要有3种计算方法：雷诺时均模拟(RANS)，大涡模拟(LES)与直接数值模拟(DNS)．相较于DNS，RANS与LES都具有计算量小、效率高的优点．但是除了DNS可以直接求解纳维-斯托克斯(Navies-Stokes)控制方程组外，RANS与LES都需要对控制方程进行时间平均或者空间滤波处理，也因此会产生未封闭项，包括雷诺应力项、标量通量项、扩散通量项、化学反应速率源项等，这些未封闭项都需要建立相应的模型进行封闭[1]．其中，化学反应速率源项，由于其湍流燃烧耦合导致的强烈非线性特征，难以直接采用阿伦尼乌斯(Arrhenius)方程进行计算，因此研究者们开始建立相应的模型来求解湍流燃烧中的化学反应．

目前被广泛应用的湍流燃烧模型有两类：小火焰(flamelet)模型与概率密度函数(PDF)模型．小火焰模型将湍流火焰假设为一系列非常薄的一维层流火焰的集合，用层流火焰的结构表征湍流火焰，使用过程变量来计算相应反应的反应速率[2-3]．小火焰模型虽然求解简单，计算成本较低，但是建立小火焰库对大量的存储资源，且需要严格满足小火焰假设．不同于小火焰模型，PDF模型通过对组分、温度等标量建立联合概率密度函数，求解相应的联合概率密度的输运方程来描述湍流燃烧过程中组分、温度等标量的分布特征[4-5]．但是当反应组分较多且反应机理复杂时，PDF模型的计算成本十分高昂．

除小火焰模型与PDF模型之外，还有一些燃烧模型也取得了较大的发展，包括条件矩(CMC)模型、线性涡(LEM)模型、二阶矩(SOM)模型等．其中CMC模型通过假定反应标量的脉动与参考标量具有特定函数关系，从而简化条件平均的反应标量传输方程，实现模型封闭[6]．LEM模型则是假定未封闭尺度下的三维湍流燃烧过程可以用一维扩散反应过程映射得出，从而实现化学反应速率源项的封闭[7]．SOM模型以及进一步发展的动态二阶矩(DSOM)模型将温度、质量分数、密度等标量进行打包，并将过滤后的化学反应速率源项展开成多项矩的和，进而通过求解矩的传输方程，计算过滤后的化学反应速率[8-11].总之，湍流燃烧模型核心在于通过假设或者传输控制方程，建立大涡模拟框架下已知量与化学反应速率的关联方程，从而实现亚网格尺度湍流燃烧的封闭.

近年来，人工神经网络(ANN)技术快速发展．得益于其强大的非线性特征拟合能力与自适应信息处理能力，ANN逐渐被应用于湍流燃烧数值模拟研究．ANN技术在湍流燃烧模型的应用主要分为两个方向：利用ANN技术耦合湍流燃烧模型，从而改进燃烧模型的性能；利用ANN技术代替湍流燃烧模型，降低湍流燃烧计算成本．Christo等[12]采用ANN技术学习PDF模型，从而得到具有PDF特征的ANN，用于计算湍流燃烧中的化学反应．Chen等[13]则是利用ANN学习原位自适应表(ISAT)中输入输出之间的非线性特征，替代直接积分(DI)降低计算成本．Sen等[14]用ANN学习LEM模型，通过学习LEM预模拟生成的数据，拟合化学反应速率与反应标量之间的关系．De Frahan等[15]用不同的机器学习技术，通过学习一个旋流直接数值模拟数据库的数据，训练出精度更高的presumed-PDF模型．目前主要的ANN燃烧模型，主要集中研究当地标量与当地化学反应速率之间的关系，一定程度上忽略了湍流对燃烧的作用，而在DSOM模型的研究中，标量场的梯度分布作为模型的重要输入，可以较好地修正因忽略亚网格湍流燃烧耦合作用带来的反应速率计算偏差，反应标量的场分布对于湍流燃烧模型的影响值得进一步探究．

1 神经网络模型

通常，燃烧过程中各反应步化学反应速率根据密度、质量分数、温度以及反应参数结合Arrhenius公式进行计算．但在网格解析尺度大于化学反应尺度与湍流尺度的大涡框架中，被过滤的化学反应速率与被过滤的密度、质量分数、温度之间的关系是难以预测的，仅仅使用化学反应速率公式与Arrhenius公式计算的化学反应速率将会严重偏离真实值．化学反应速率计算公式为：

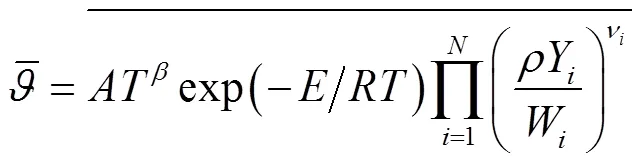
本研究中构造人工神经网络，解析被过滤的化学反应速率与被过滤的密度、质量分数、温度之间的复杂关系．人工神经网络采用主流的多层感知机(multi-layer perceptron，MLP)神经网络结构[16]，包含一层输入层(input layer)、一层隐藏层(hidden layer)以及一层输出层(output layer)，如图1所示．

模型以大涡模拟框架下过滤后的化学反应速率为输出．为了降低神经网络拟合难度以及提升计算效率，首先将过滤后的密度、质量分数、温度以及反应参数进行打包，转换成对应的质量分数-密度标量R＝ρY和温度指数标量＝exp(−/)作为输入，构造ANN模型．为了研究湍流影响的标量场分布对化学反应速率计算的作用，基于相同的神经网络结构，增加了相应的梯度矢量作为输入，构造梯度输入人工神经网络(ANN-G)模型．模型均采用反向传播监视学习算法进行参数修正，利用变学习速率算法加速神经网络训练过程，并使用Relu激活函数提升模型非线性拟合能力．当神经网络模型训练完成后，模型输出可以表达为输入与训练参数的函数：

图1 神经网络结构示意

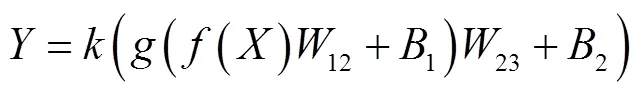
式中：W和B分别为神经网络训练得到的权重值与偏置值；、、则是各层神经网络的激活函数．

经训练后的神经网络则可作为湍流燃烧模型，通过输入过滤后的质量分数-密度标量与温度指数标量，计算过滤后的化学反应速率．

2 模型训练

2.1 训练数据集

本研究采用一个贫燃预混火焰的DNS数据库提供神经网络模型训练与验证的数据[17]．该贫燃预混火焰由中心射流与伴随流组成，如图2所示．入口喷嘴的宽度为2.4mm．中心射流的入流平均速度为100m/s，温度为800K，压力为0.4MPa，由当量比为0.7的甲烷和空气的混合物组成．伴随流的入流平均速度为15m/s，由甲烷/空气完全燃烧的高温产物组成．入口喷嘴处雷诺数达到11200，完全发展区域的卡洛维茨数为20～40，科尔莫戈洛夫尺度为25μm．直接数值模拟计算域为24×16×4.26，计算域网格采用均匀立方体网格，网格尺寸＝20μm，总网格数为2.8亿．化学反应机理采用16种组分、72步反应的贫燃预混骨架反应机理[18].

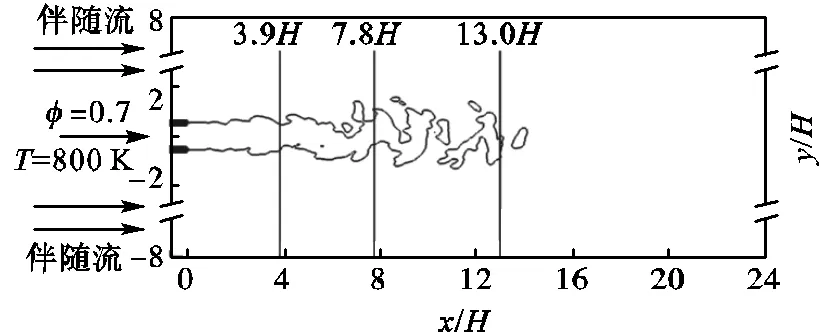
图2 预混燃烧直接数值模拟结构

大涡模拟的控制方程实际求解的是空间平均量，因此需要采用空间滤波函数[1]对直接数值模拟数据进行过滤．常用的空间滤波函数是盒式滤波函数，方程如下：

式中：为过滤尺度，考虑到大涡模拟的网格尺度一般在0.1～1mm之间，本研究采用0.16mm与0.32mm作为假定的大涡模拟网格尺寸，相当于8倍与16倍的直接数值模拟网格尺寸，以此对直接数值模拟数据进行空间过滤，获取特征火焰区共计1200000与150000条数据用于先验性研究，训练数据与测试数据占比分别为0.8与0.2．选择反应机理中化学反应区域较薄的关键反应步(R1)进行主要研究，以及化学反应区域较厚的关键反应步(R2)用作对比验证[19]．特征反应步参数如表1所示．

表1 甲烷燃烧机理特征反应步参数

Tab.1 Parameters of special reaction steps of the mechanism of CH4 combustion

2.2 超参数优化

超参数是神经网络中在训练前预设的无法通过训练过程自动调整的参数，包括隐藏层神经元数、初始学习速率、最大迭代步数．超参数的选定对神经网络的训练有较大影响，因此本节将对神经网络模型的超参数进行优化研究．由于ANN模型与ANN-G模型采用同样的网络结构，且在参数调整研究中表现十分相似，所以本节仅讨论ANN模型的结果．

图3表示模型在不同隐藏层神经元数的条件下的误差．模型误差采用均方根误差(MSE)计算，是表征模型的预测输出与目标输出之间误差的特征，误差越接近0，表示模型精确度越高．由图可见，随着隐藏层神经元数的增加，模型误差逐步减小．当隐藏层神经元数超过60以后，模型误差变化幅度很小，而且基本上稳定在0.003以下，说明此时输入与输出之间的函数关系已经得到充分解析．更多的隐藏层神经元数能带来更好的预测能力，同时也意味着更高的计算成本，此外过多的隐含层神经元也会带来过拟合的风险，所以需要选择一个适中的隐藏层神经元数来平衡模型的计算成本与精度．图4表示模型在不同学习速率条件下的误差，当学习速率大于0.025时，图中误差随着学习速率的增大而明显增大；而当学习速率小于0.025时，模型误差稳定在0.003以下．由于学习速率控制着神经网络模型迭代过程中与的变化率，较高的学习速率虽然能加快模型的训练过程，但是也会放大训练过程中的误差，导致模型劣化．图5表示训练模型在不同最大迭代步数条件下的误差．排除随机性的波动，误差受最大迭代步数变化的影响并不明显．综上所述，本研究中的神经网络的超参数设置为：隐藏层神经元数为60，初始化学反应速率为0.01，最大迭代步数为7000．

图3 不同隐藏层神经元数的神经网络的误差

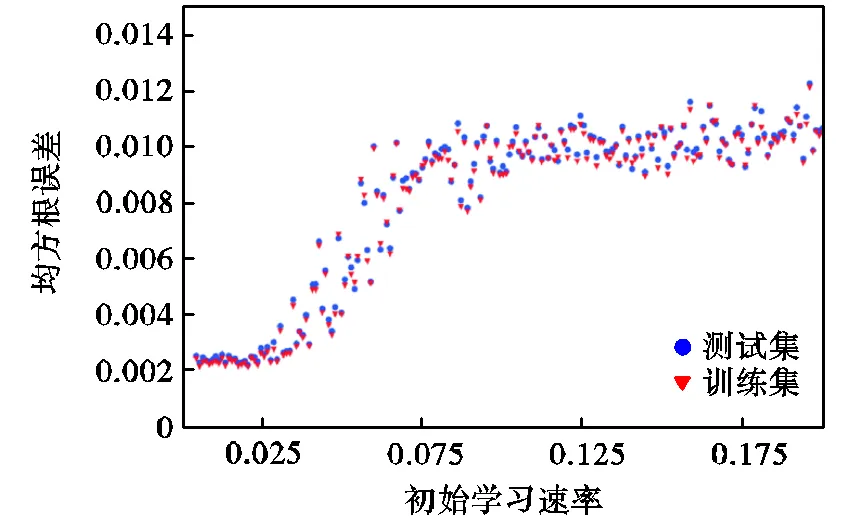
图4 不同初始学习速率的神经网络误差

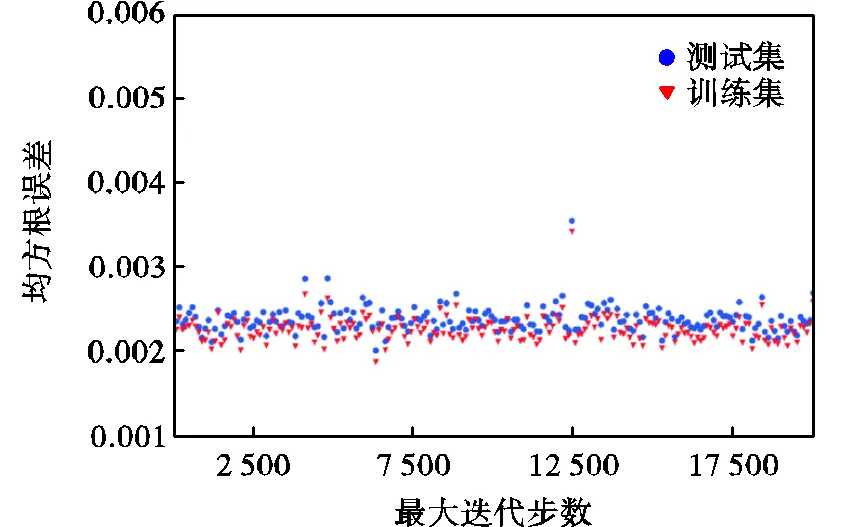
图5 不同最大迭代步数的神经网络误差

3 结果与讨论

3.1 对比验证

为了验证ANN模型与ANN-G模型的准确性，引入层流化学封闭(LCC)模型的结果作为对照[20].  3个模型均采用相同的基元反应空间过滤的标量计算化学反应速率，而以DNS数据计算的化学反应速率的空间过滤值为参考值．为了表征化学反应速率的预测值与准确值之间的误差，定义二次误差ε，公式如下[21]：

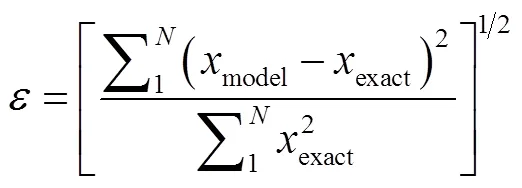
表2是3个模型的二次误差值．其中，LCC模型的误差最大，达到了6.936；ANN模型误差较小，仅为0.255，是LCC模型误差的3.68%．而ANN-G模型，在考虑了标量分布后，误差进一步降低至0.157. 对于薄反应区域的化学反应，LCC模型计算的化学反应速率与参考结果相去甚远，而两个神经网络模型都更能准确预测薄反应区域的化学反应速率．且考虑了标量分布的ANN-G模型，精确度还能进一步提升．

表2 不同模型二次误差值

Tab.2 Quadratic errors for different models

图6表示3个模型的化学反应速率预测值与准确值的散点图，图中红线是斜率为1的参考线，表示DNS参考值的位置．可以看出，ANN-G模型与ANN模型的预测值与准确值的分布整体上能保持线性；ANN-G的结果相对更好一些，在参考值的红线附近更为集中．而LCC模型的结果则偏离准确值10倍以上，表现出了极大的误差，也进一步说明LCC模型采用反应标量的空间平均值无法直接计算化学反应速率．

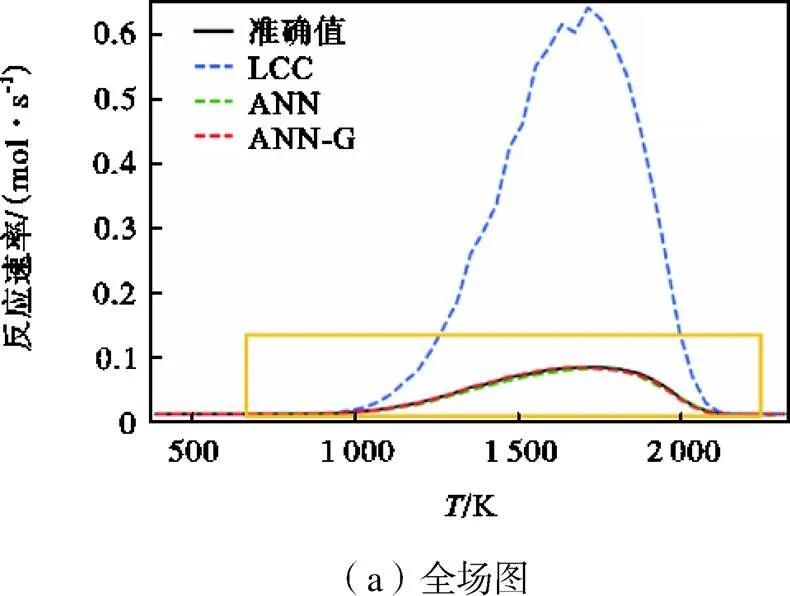
图7表示不同模型预测的化学反应速率的温度条件统计分布图，其中(b)图是(a)图红框范围的局部放大图．由图可见，LCC对化学反应速率的预测误差极大．而ANN-G模型与ANN模型整体表现优异，无论是在波峰峰值、波峰位置或者是波峰宽度上，预测分布都十分接近真实分布．相对而言，ANN-G模型比ANN模型更加准确，因为ANN模型略微低估了峰值，而且在高温区域甚至出现了负反应速率的情况．

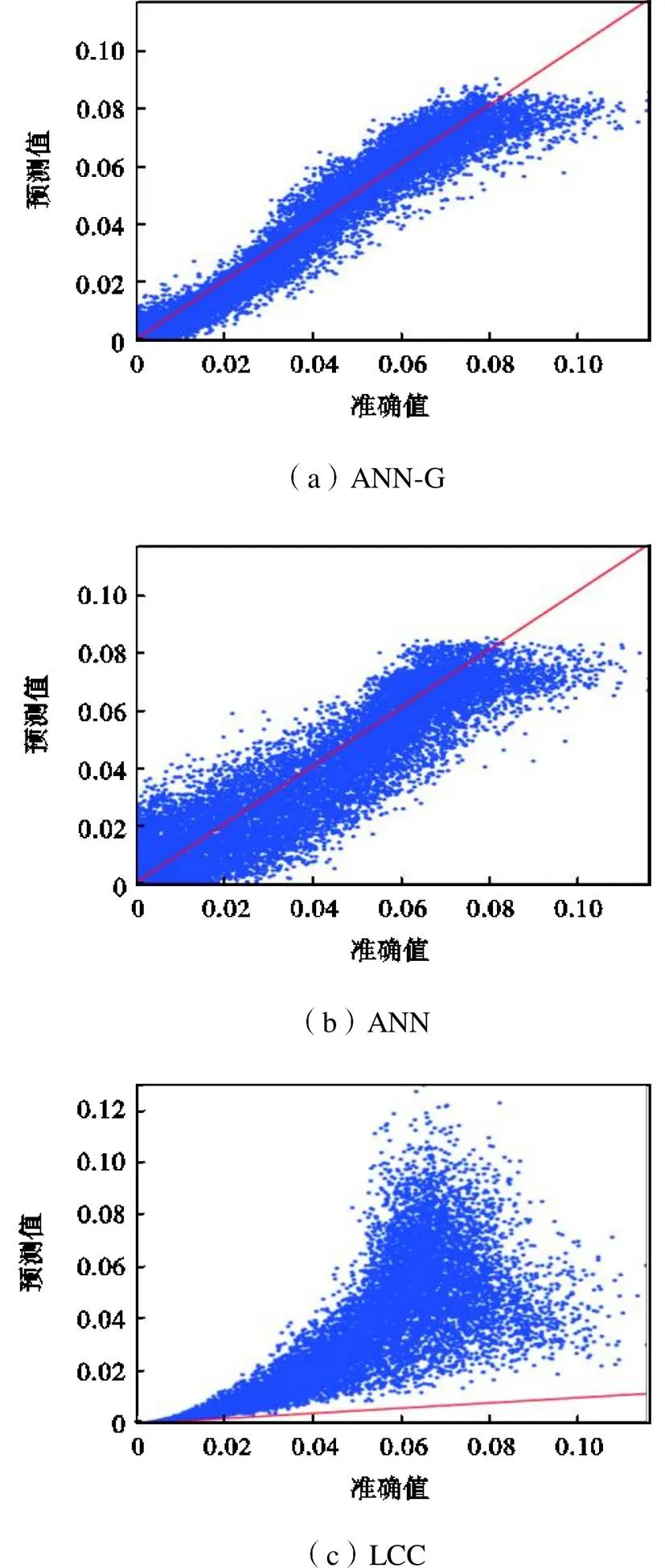
图6 模型预测值与准确值的散点图

3.2 泛化验证

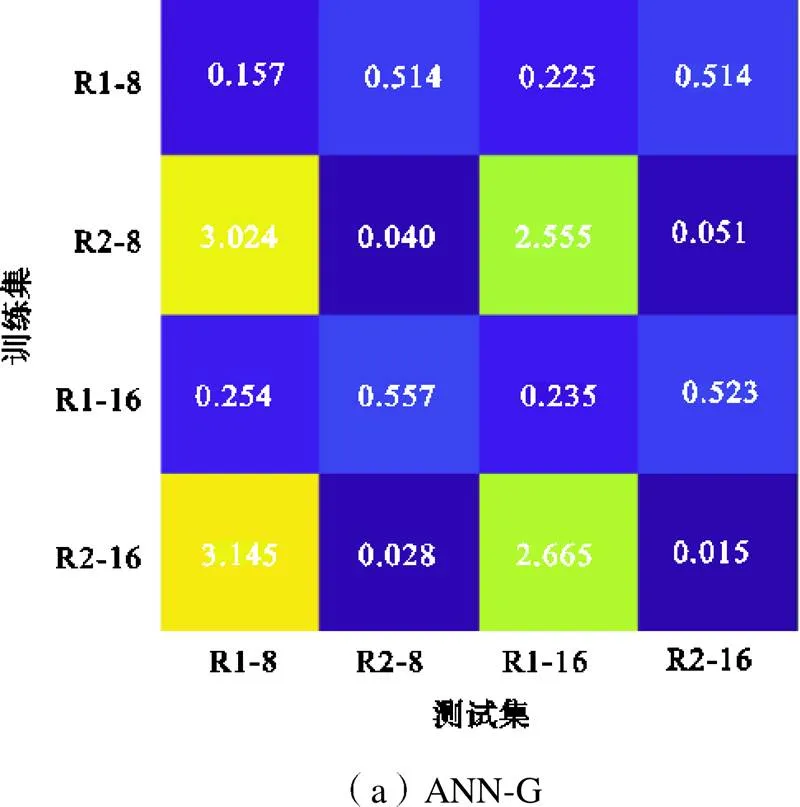
在前文的神经网络模型训练中，通过交叉验证已经初步证明了神经网络模型的泛化能力．但无论是训练、验证或者测试，都是基于8倍过滤尺度的反应步(R1)的数据．而神经网络方法训练得出的模型应用于其他的过滤尺度或者其他的反应步时，模型的精确性需要进一步检验．因此，本研究采用不同过滤尺度(8，16)与不同反应步(R1，R2)的训练集训练神经网络模型，并将模型应用于其他条件下生成的测试集，从而检验发展的统一的神经网络模型，应用于其他过滤尺度与反应步上的模型精确度．根据训练集与测试集的差异，构成16种测试条件．图8是不同测试条件下模型的误差结果热力图．从图中可以看出，ANN模型与ANN-G模型在不同条件下的测试误差都能控制在较小的范围内(小于3)，相对而言，LCC模型其误差则是将近7．充分证明了神经网络模型相对于LCC模型的优越性．此外，从验证结果中发现，本数据集训练的模型应用于本数据集测试的情况下，误差最小，对应于从左上到右下的斜线方块，这与预期相符；对于同一个反应步的训练集ANN-G模型，小尺度过滤训练集的模型精确度普遍比大尺度过滤训练集模型精确度更高，说明更精确的数据集有利于训练更精确的模型；而对于同一个过滤尺度的训练集ANN-G模型，(R1)训练集模型的精确度普遍比(R2)训练集模型的更高．这表明可以采用小尺度过滤的(R1)反应步训练集ANN-G作为一个适用范围更广泛的燃烧模型．而对于ANN模型，几乎在所有验证条件下，模型精度都比ANN-G模型更低．

4 结 论

本研究采用神经网络方法建立了准确求解过滤化学反应速率的ANN模型以及考虑了标量场梯度输入的ANN-G模型．通过对神经网络进行超参数优化，确定了最优神经网络超参数配置．并且将ANN模型、ANN-G模型与LCC模型的先验结果进行对比验证，发现对于薄反应区反应，LCC模型的误差较大，而ANN模型与ANN-G模型，都能准确地计算化学反应速率，误差只有LCC模型的3.68%和2.26%.而相较于ANN模型，考虑湍流影响，增加标量场梯度矢量为输入的ANN-G模型具有更高的准确度，计算误差进一步降低．在神经网络模型的泛化验证中发现，基于特定过滤尺度与特定基元反应发展的ANN模型和ANN-G模型具有一定的泛化能力，能在其他的过滤尺度和基元反应上保证较高的精度.而且小尺度过滤的(R1)反应步训练集ANN-G模型具有更广泛的应用潜力．未来，神经网络模型可以进一步应用于大涡模拟框架下的后验性研究，进一步探究神经网络在燃烧模型的改进和开发中的应用．

［1］ 白 云. 煤粉气固湍流燃烧火焰特性及其直接矩燃烧模型的研究[D]. 杭州：浙江大学能源清洁利用国家重点实验室，2018.

Bai Yun. Studies on Flame Characteristics and Direct Moment Closure Model for Pulverized Coal Gas-Solid Turbulent Combustion[D]. Hangzhou：State Key Laboratory of Clean Energy Utilization，Zhejiang University，2018(in Chinese).

［2］ Fiorina B，Gicquel O，Vervisch L，et al. Approximating the chemical structure of partially premixed and diffusion counterflow flames using FPI flamelet tabulation[J].，2005，140(3)：147-160.

［3］ Perry B A，Mueller M E，Masri A R. A two mixture fraction flamelet model for large eddy simulation of turbulent flames with inhomogeneous inlets[J].，2017，36(2)：1767-1775.

［4］ Gordon R L，Masri A R，Pope S B，et al. Transport budgets in turbulent lifted flames of methane autoigniting in a vitiated co-flow[J].，2007，151(3)：495-511.

［5］ Bulat G，Jones W P，Marquis A J. Large eddy simulation of an industrial gas-turbine combustion chamber using the sub-grid PDF method[J].，2013，34(2)：3155-3164.

［6］ Roomina M R，Bilger R W. Conditional moment closure(CMC)predictions of a turbulent methane-air jet flame[J].，2001，125(3)：1176-1195.

［7］ Sen B A，Menon S. Linear eddy mixing based tabulation and artificial neural networks for large eddy simulations of turbulent flames[J].，2010，157(1)：62-74.

［8］ Zhou L X，Qiao L，Chen X L，et al. A USM turbulence-chemistry model for simulating NOformation in turbulent combustion[J].，2002，81(13)：1703-1709.

［9］ Luo K，Yang J，Bai Y，et al. Large eddy simulation of turbulent combustion by a dynamic second-order moment closure model[J].，2017，187：457-467.

［10］ Luo K，Liu R，Bai Y，et al. Large eddy simulation of turbulent partially premixed flames with inhomogeneous inlets using the dynamic second-order moment closure model[J].，2020，24(4)：1-20.

［11］ Luo K，Liu R，Bai Y，et al.andstudies of a direct moment closure approach for turbulent combustion using DNS data of a premixed flame[J].，2021，38(2)：3003-3011.

［12］ Christo F C，Masri A R，Nebot E M，et al. An integrated PDF/neural network approach for simulating turbulent reacting systems[J]()，1996，26(1)：43-48.

［13］ Chen J Y，Blasco J A，Fueyo N，et al. An economical strategy for storage of chemical kinetics：Fittingadaptive tabulation with artificial neural networks[J].，2000，28(1)：115-121.

［14］ Sen B A，Hawkes E R，Menon S. Large eddy simulation of extinction and reignition with artificial neural networks based chemical kinetics[J].，2010，157(3)：566-578.

［15］ De Frahan M T H，Yellapantula S，King R，et al. Deep learning for presumed probability density function models[J].，2019，208：436-450.

［16］ Luo K，Xing J，Bai Y，et al. Prediction of product distributions in coal devolatilization by an artificial neural network model[J].，2018，193：283-294.

［17］ Luca S，Attili A，Schiavo E L，et al. On the statistics of flame stretch in turbulent premixed jet flames in the thin reaction zone regime at varying Reynolds number[J].，2019，37(2)：2451-2459.

［18］ Luca S，Al-Khateeb A N，Attili A，et al. Comprehensive validation of skeletal mechanism for turbulent premixed methane-air flame simulations[J].，2018，34(1)：153-160.

［19］ Peters N. Numerical and asymptotic analysis of systematically reduced reaction schemes for hydrocarbon flames[G]//. Berlin：Springer，1985：90-109.

［20］ Potturi A S，Edwards J R. Investigation of subgrid closure models for finite-rate scramjet combustion[C]// 43. 2013，AIAA 2013-2461.

［21］ Wall C，Boersma B J，Moin P. An evaluation of the assumed beta probability density function subgrid-scale model for large eddy simulation of nonpremixed，turbulent combustion with heat release[J].，2000，12(10)：2522-2529.

-Analysis of a New Combustion Model Based on Artificial Neural Network Method

Liu Runzhi，Luo Kun，Xing Jiangkuan，Fan Jianren

(College of Energy Engineering，Zhejiang University，Hangzhou 310027，China)

A new artificial neural network(ANN)based combustion model has been developed by modelling the non-linear relationship between the accurate chemistry reaction rate and the known scalars based on the ANN method. With the Dynamic Second-order Moment Closure model for reference，the gradient of the scalar distribution is added as extra input variable，and the artificial neural network with gradient input(ANN-G)model is then developed. The two models have been validated in theanalysis on the basis of the direct numerical simulation database of a premixed flame. It is observed that both the ANN model and the ANN-G model can predict the chemical reaction rate more accurately than laminar chemistry closure model，especially for the reaction steps in the thin reaction zone. In addition，the ANN-G model has better performance than the ANN model in the generalization validation.

turbulent combustion；artificial neural network；combustion model；analysis

TK11

A

1006-8740(2022)04-0433-07

10.11715/rskxjs.R202206003

2021-03-25．

国家自然科学基金资助项目(91741203).

刘润之（1996—  ），男，博士研究生，ringsliu@zju.edu.cn.

罗 坤，男，博士，教授，zjulk@zju.edu.cn.

(责任编辑：隋韶颖)