基于集成式神经网络的扁平箱梁颤振导数预测

梅瀚雨 ，王 骑 ,2，廖海黎 ,2，张 岩

（1.西南交通大学土木工程学院，四川 成都 610031；2.西南交通大学风工程四川省重点实验室，四川 成都610031）

随着桥梁跨径的不断增加，缆索承重桥梁呈现阻尼低、刚度小等特点，这也使得桥梁对风的敏感性逐渐增加，其在强风作用下发生颤振失稳的风险增加.尽管风洞试验技术已比较成熟，但仍存在试验周期长、试验成本高等问题，不便于在初步设计阶段开展，增加了方案比选工作的难度.此时，若能借助比较准确的颤振导数，则可以采用颤振理论计算获得对应的颤振风速，快速完成不同方案气动稳定性的比选工作.

颤振导数表征桥梁断面的气动自激力特性，也是颤振分析理论最重要的气动参数，由Scanlan等[1]首次提出，并被广泛应用.除薄平板的颤振导数存在理论解析解，桥梁断面的颤振导数一般通过强迫振动风洞试验[2-4]或自由振动风洞试验[5-7]获得，前者精度虽高但需专用设备，后者简便易行但精度较低.也可基于计算流体动力学（CFD）数值模拟的强迫振动测试技术[8-10]进行颤振导数的识别工作.无论哪种风洞试验识别方法，都存在花费较高、周期较长的问题，CFD数值模拟技术仍存在识别精度偏低、计算周期长等问题.鉴于目前已积累了较多的扁平箱梁气动参数数据，若能提出一种高效准确的方法，能够实现利用已有桥梁断面的颤振导数而预测出新设计桥梁断面的颤振导数，不但有效利用了历史数据，还能够显著推进新建桥梁的方案选型工作.

近年来，基于数据驱动的机器学习方法在桥梁风工程领域展现了其强大的参数识别和预测能力，诸多学者利用机器学习方法开展了颤振导数识别研究：Jung等[11-12]基于 Matsumoto等[13]识别的矩形断面颤振导数数据库，分别利用神经网络和支持向量机算法建立了颤振导数预测模型； Wu等[14]利用基于元胞机优化的人工神经网络预测了桥梁断面非线性气动响应；李乔等[15]等用人工神经网络系统识别了桥梁断面的静力三分力系数； Li等[16]基于某大跨度悬索桥现场实测数据，利用决策树模型和支持向量机回归模型对涡激共振事件分别进行了模态分类的模型构建和涡振响应回归模型的构建；陈讷郁等[17]利用人工神经网络识别了典型桥梁断面的气动参数，其中，静力三分力系数识别结果较好，但颤振导数的预测结果较差；Rizzo等[18]利用人工神经网络预测了闭口箱梁悬索桥的颤振临界风速，但实现方法较为繁琐，难以展现其工程应用价值.

以上结果表明，机器学习方法可以有效地应用到桥梁风工程领域，且研究成果对于工程设计有较高的参考价值.针对桥梁断面颤振导数预测的问题而言，神经网络方法凭借其强大的多目标预测能力已展现出较大的优势.然而，前述研究成果对于算法的实现和数据集的处理缺乏系统性地描述，具体算法各不相同，识别精度也参差不齐，使得该方法难以真正推广到工程设计领域.

为了利用机器学习强大的推演能力，同时避免不同算法的不足，本文提出了利用集成式深度神经网络模型来预测桥梁断面颤振导数的方法.基于集成学习，构建包含30种不同网络结构的子神经网络模型，并利用15种典型扁平箱梁的颤振导数作为神经网络的学习样本，最后对子神经网络模型的预测结果进行组合和评判，可得到任意扁平箱梁颤振导数的预测值.测试结果表明：本文提出的模型可以深度挖掘扁平箱梁气动外形与颤振导数的潜在关系，仅利用60%的数据集进行模型训练即可根据断面形状高精度预测8个颤振导数，其结果优于多项式回归模型和单一人工神经网络模型.本文所提的扁平箱梁颤振导数的预测方法方便实现，可以应用到桥梁初步设计阶段不同方案的颤振计算中.

1 数据准备

作为典型的监督学习问题，建立必要的数据集是建立神经网络预测模式的基础.数据集是由输入特征x（自变量）和对应的预期输出R（因变量）所组成，神经网络的作用在于建立隐式的映射关系R=f（x;δ），其中： δ 为待训练参数；f为映射关系.根据这一原理，并结合扁平箱梁的外形特征，在本研究中，输入特征x确定为箱梁的外形尺寸特征和折算风速，预期输出R为该折算风速下的8个颤振导数值.数据集的数据分布应尽可能覆盖本研究所涉及的应用领域，以方便设计人员的使用.一般地，模型训练所必需的数据集可通过收集文献资料获取.然而，考虑到数据来源和数据精度，本次研究所采用的数据集全部来源于风洞试验所获取的典型扁平箱梁断面颤振导数.

1.1 颤振导数数据集获取

本次试验对象为15种不同气动外形的扁平箱梁断面，如图1和图2所示，包含有3种不同的梁高H（36、44 m m 和 57 m m ）和 5 种不同的斜腹板倾角θ（24°、21°、18°、15°和 12°）.为方便模型的装配，制作的模型宽度B= 400 m m ，高度有所变化，模型宽高比分别为11、9和7.颤振导数涵盖的折算风速V范围为 4～18，风攻角 α =0°，+3° 和 +5°.为了对扁平箱梁断面的气动外形特征进行更为简单且方便的描述，本次试验模型不涉及附属结构设施，例如桥面栏杆、中央稳定板等.为减小模型自身惯性力且保证模型刚度，试验模型均采用碳纤骨架联合PVC蒙皮制作，质量为2.0～2.4 kg.

图1 典型断面示意Fig.1 Typical section schematic

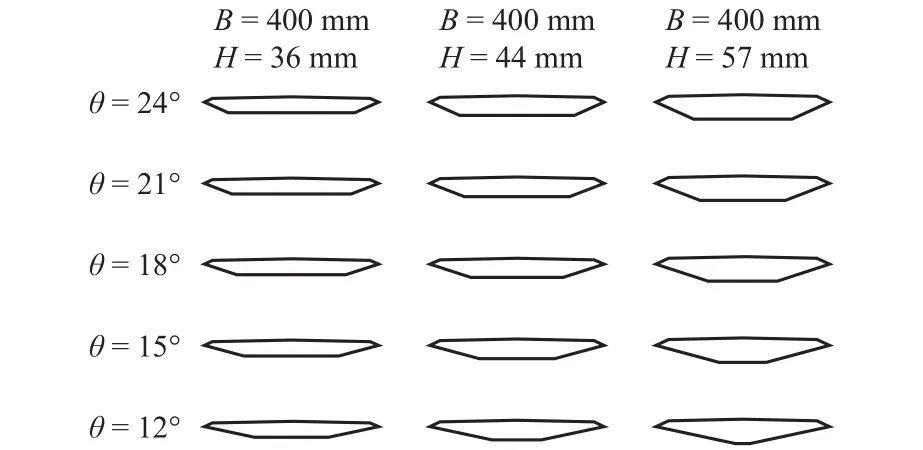
图2 扁平箱梁模型断面Fig.2 Sectional models of flat box girders

本次强迫振动风洞试验在西南交通大学XNJD-1风洞中进行，如图3所示.颤振导数的设备及识别方法可参考文献[19-20]，结合所提取的自激力，可以识别不同折算风速下的8个颤振导数和.

图3 安装在风洞中的强迫振动装置及模型Fig.3 Sectional model assembled on forced vibration device in wind tunnel

通过设计的自由振动颤振试验，获得不同模型在不同风攻角下（0°、+3°、+5°）的颤振临界风速，并和由颤振导数计算的颤振临界风速进行对比，由此验证颤振导数的准确性.颤振计算分析方法采用Chen等[21]提出的弯扭耦合颤振闭合解法，自由振动风洞试验采用传统的弹簧悬挂节段模型实现（图4），两者选用的质量和动力参数一致.以B=400mm，H=44mm，θ=21° 断面为例，表1中所示其颤振临界风速计算值和试验值的一致性表明了颤振导数测试的准确性.

图4 弹簧悬挂自由振动风洞试验Fig.4 Free vibration wind tunnel tests

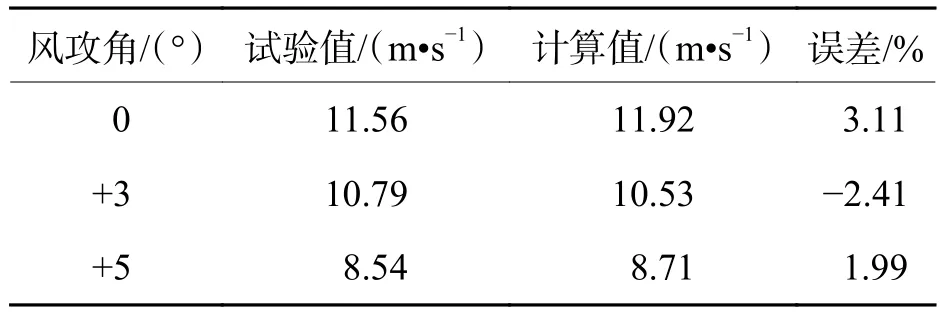
表1 颤振临界风速结果对比Tab.1 Comparison of critical flutter wind speeds

1.2 数据预处理

为保证数据集的完整性、唯一性、准确性，需对利用强迫振动风洞试验所获得的实验数据进行一定的数据清洗[22].结合1.1节自由振动风洞试验的结果，剔除无效的、精度不足的数据样本，最终获得样本大小为525的数据集.每条数据样本包含某一扁平箱梁断面在竖向或扭转运动状态某一折算风速下的8个颤振导数.为表征扁平箱梁气动外形特征，文献[17]利用宽高比、横向坡度、底板宽度比等无量纲参数进行描述.本次研究采用最为直接的方式进行特征描述，即：利用扁平箱梁断面7个顶点（A～G）相对于断面形心的二维坐标进行描述（如图5所示），图中：U为来流风速.这种描述方式较为简单且易于推广，可以更好地量化来流风攻角的影响.

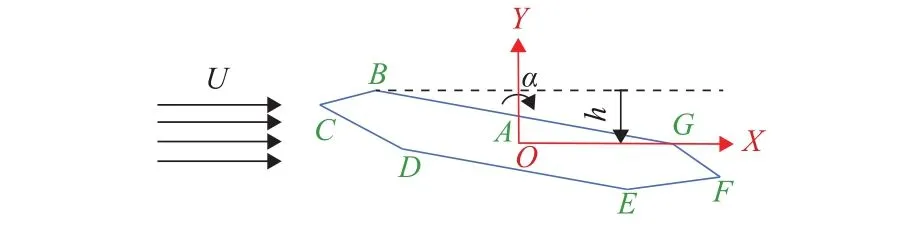
图5 带风攻角的断面顶点坐标示意Fig.5 Coordinate of flat box girder with angle of attack

假设扁平箱梁断面某一顶点坐标为（a,b），风攻角为 α ，将每个顶点坐标进行旋转操作并进行无量纲化则可得到转换后的顶点坐标为（x,y）, 如式（1）.

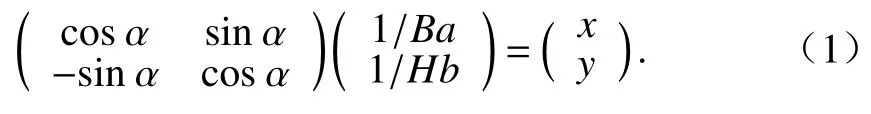
由于不同特征和目标的来源、量级以及量纲是不同的，造成特征值分布范围过大，从而降低神经网络梯度下降过程的效率，收敛缓慢.因此，在模型训练之前，需要对数据样本进行特征值缩放，即特征归一化.本次研究采用标准归一化方式（z-score method），使得每一维度的特征都符合标准正态分布.对于每一个维度特征sk（包含预测目标），标准归一化后的特征可表示为

式中： µ (sk) 和 σ (sk) 分别为第k个特征sk的均值 和标准差.

实际桥梁断面一般为对称结构，若使用7个顶点坐标，则包含了过多冗余信息，如点B与点G对称.因此，为了精简模型特征参数、加快收敛速度、提高模型的泛化能力，只保留A、B、C和D4个顶点的坐标作为输入特征.

综上，本次训练的模型包含有9个输入特征，其中 8个为 4个顶点坐标 (xA,yA,xB,yB,xC,yC,xD,yD) ，1个为折算风速V；包含有8个输出目标值，即8个颤振导数.

2 集成式深度神经网络模型

2.1 神经网络

神经网络方面的研究始于1943年Mcculloch和Pitts[23]提出的M-P模型.该模型包含有一个神经元，可以接收来自上一层其他n个神经元传递的输入信号并伴随有不同的权重.神经元收到的输入信号将与该神经元的阈值进行比较并通过激活函数进行非线性变换，从而产生该神经元的输出信号.深度神经网络是M-P模型的拓展，可简单理解为包含有多个隐藏层和多个神经元的神经网络.随着神经网络深度的增加，权重和阈值的数量逐渐增加，如何进行参数寻优便依赖于深度神经网络的前向传播和反向传播算法，可参考文献[24].

2.2 集成式深度神经网络模型构建

神经网络的结构主要取决于输入层维度、隐藏层数、隐藏神经元个数以及输出目标维度.隐藏层数和神经元个数增多，神经网络对特征信息的提取能力会增强，但同时也会产生计算资源消耗以及过拟合现象.若隐藏层数和神经元个数不足，则可能出现欠拟合现象，即神经网络无法挖掘有效信息.这使得目前对于隐藏层数和隐藏神经元个数的取值仍在一定程度上依赖于设计经验.

为了避免单个神经网络模型在算法上的不足，Dasarathy等[25]在1979年提出集成学习（ensemble learning, EL）思想：一种通过构建并结合多个学习器（决策树，神经网络等）来完成学习任务的机器学习策略.集成学习的基本思路为：构建多个不同结构的“个体学习器”，利用独立采样的数据进行并行或串行模型训练，最后利用某种策略（加权平均）对不同“个体学习器”的结果进行结合.相较于单一学习器（图6），集成学习模型降低了超参数调整的困难，且通常可获得优越的泛化性能.

图6 子神经网络预测颤振导数Fig.6 Sub-network for flutter derivative prediction

经反复测试和验证，本研究确定采用含有30个不同网络结构的个体神经网络（简称“子神经网络”）的并行集成模型：既能取得较好的预测效果，又能兼顾较高的计算效率.其中，模型包含的每个子神经网络结构形式均与图6所示的子神经网络类似.各子神经网络包含有不同的隐藏层层数、隐藏神经元个数和非线性激活函数，相关信息如表2所示.

表2 不同子神经网络结构设计参数Tab.2 Design parameters of different sub-neural networks

为了训练和评估本文提出的集成式深度神经网络模型，首先将本文的数据集（525组）划分为训练集（510组）和测试集（15组），其中：每一组测试集为随机选取的某一断面在某一攻角下的8个颤振导数，折算风速范围为4～18，间隔为1；训练集为余下的510组数据样本.将训练集再次划分为30个子训练集，每个子训练集包含有17组数据样本.为保证每个子神经网络训练数据的差异性和多样性，从而获得更高的泛化能力，每轮选取29个子训练集（即493个数据样本）作为一个子神经网络的训练数据，总共30轮，对应30个不同的并行子神经网络.具体的算法流程如图7所示，图中： βj为加权系数.

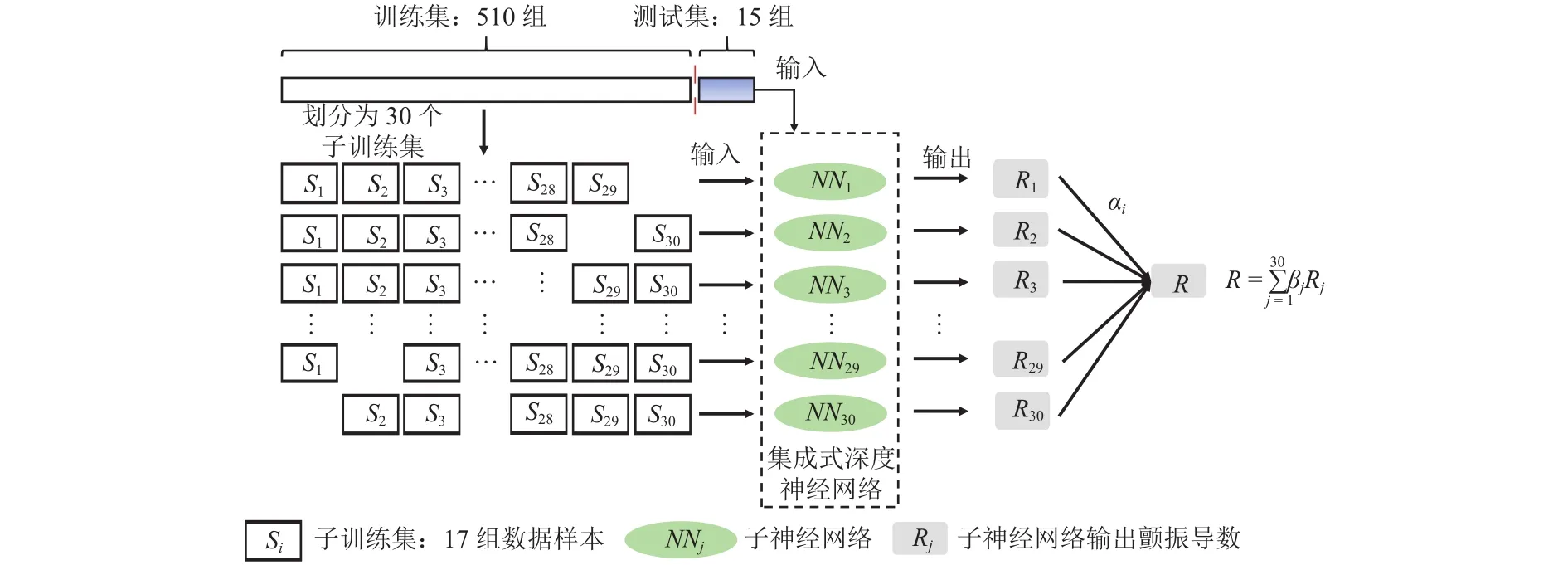
图7 集成式深度神经网络实现流程Fig.7 Flow chart of building the integrated deep neural network

由图7可以看出，每个子神经网络所输出的8个颤振导数由R进行组合输出，其中：R包含了8 个颤振导数和.研究表明[26]：相较于加权平均（ βj不同）而言，简单平均方法（ βj相同）可以获得更为稳定的模型且不容易出现过拟合问题，从而使得集成模型的泛化能力提高.因此，本文采用简单平均方法，取 βj= 1 /30 ，分别将30个不同子神经网络输出的8个颤振导数进行组合，得到最终的8个颤振导数预测值.

相比于普通的深度神经网络模型而言，集成式深度神经网络包含有如下两个优点：1） 每组数据样本分别经过了29个子神经网络模型的并行训练，使得数据集的利用率提高；2） 具有不同结构的子神经网络虽然性能各异，但集成后模型的输出结果更为稳定，并从一定程度上避免了复杂繁琐的超参数调整过程，降低了欠拟合和过拟合的风险.

3 颤振导数预测及评价

3.1 评价指标

除上文所述的子神经网络中隐藏层层数、隐藏神经元个数和非线性激活函数等与网络结构相关的超参数，深度神经网络的误差反向传播过程中还包含有其他需要预先确定的超参数，例如：学习率（即权重和偏置梯度更新的下降速率）、优化器类型等.本次研究设置30个子神经网络的学习率为0.001，权重优化器采用Adam[27]，通过梯度下降法最小化每个子神经网络的损失函数.损失函数Loss均采用如式（3）所示的均方误差函数.

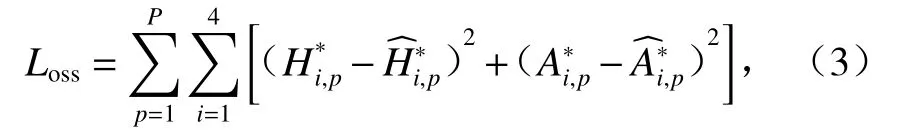
为了合理地评价本文提出的集成式深度神经网络的预测性能，采用平均绝对误差MAE、均方根误差RMSE和决定系数R23种不同的评价指标，如式（4）.需要说明的是：模型评价应基于未参与模型训练的测试集（如图7所示），即：包含了15组数据（15个折算风速）的某一随机选取的断面在某一风攻角下的8个颤振导数.

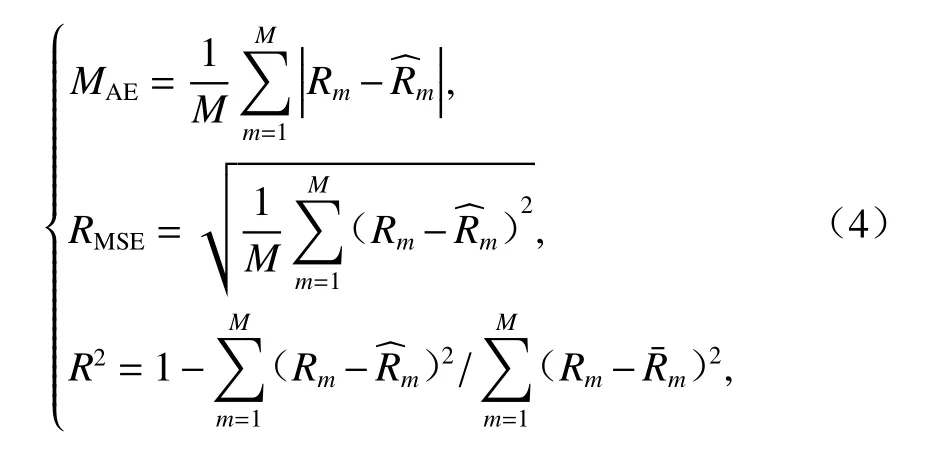
式中：Rm为某一颤振导数真实值；为其对应的神经网络预测值；M=15 为测试集大小；为15组颤振导数均值.

显然，MAE和RMSE越低，R2越接近于 1，表示模型的预测性能越好.

3.2 预测结果

基于Pytorch深度学习框架，实现了如图7所示的集成式深度神经网络模型，并利用风洞试验所获取的扁平箱梁颤振导数数据集对神经网络模型进行训练.经测试，本文所提出的预测模型训练效率较高，利用配置普通的电脑（CPU：i7-7700HQ）即可在3 min内完成模型训练（仅调用CPU），其原因在于本模型无需进行繁琐的超参数寻优过程.随机选取了如图8所示的0° 攻角下扁平箱梁断面作为预测对象，预测内容包含折算风速4～18下的8个颤振导数.

图8 测试断面详图Fig.8 Detailed geometry of testing section

图9为测试断面8个颤振导数预测结果对比，由图可以看出：在折算风速4～18范围内8个颤振导数预测值与试验值吻合较好.尽管两者在数值上有略微的差异，但整体趋势保持一致，且预测值较为平滑.

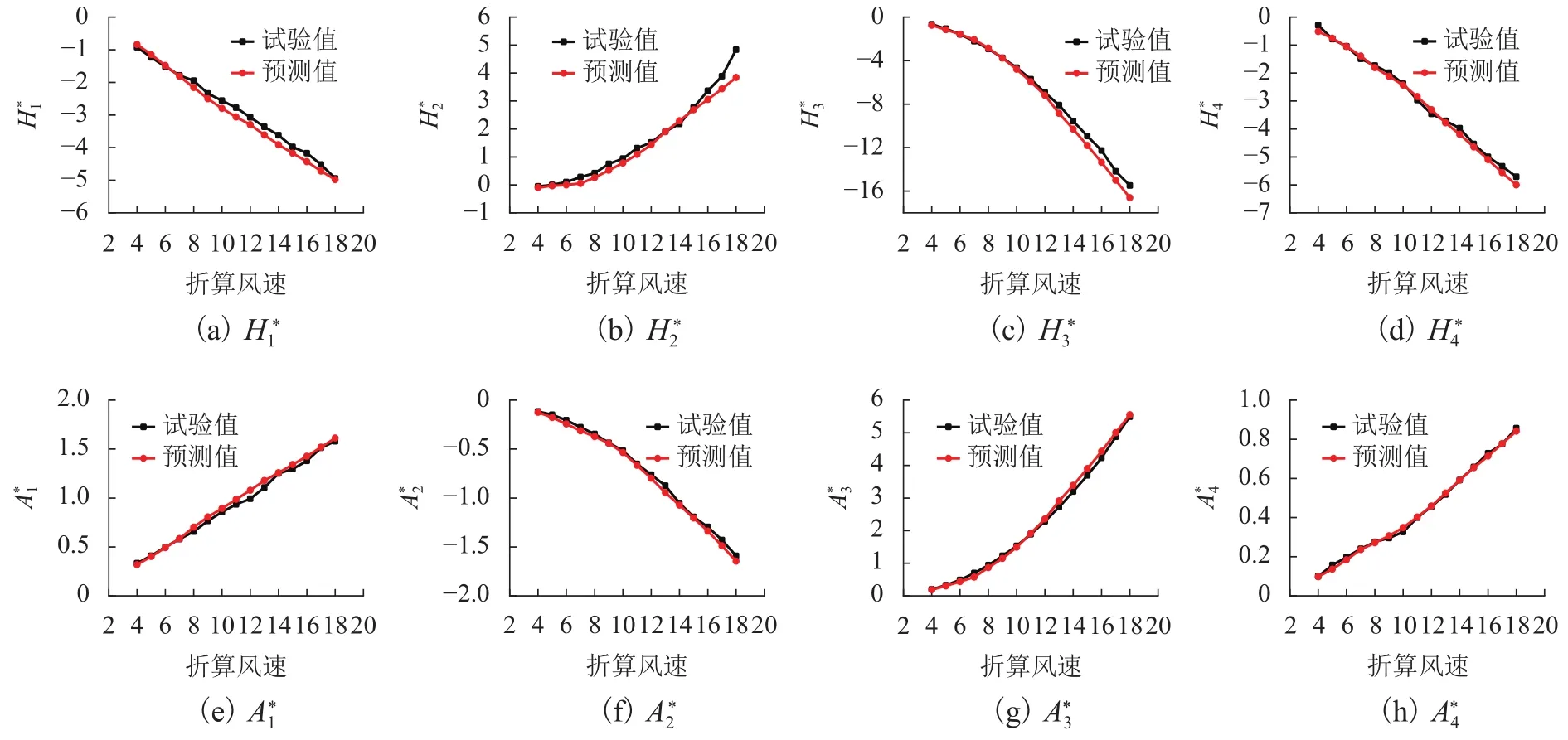
图9 测试断面颤振导数预测结果对比Fig.9 Comparison between predicted and tested flutter derivatives of testing section

图10 为测试断面颤振导数误差，由图发现：各颤振导数预测误差MAE和RMSE较小，R2均在0.950以上，最高可以达到0.998；与自激力矩相关的 4 个颤振 导 数的MAE和RMSE低于与自激升力相关的预测结果，但决定系数R2结果较为接近；弯扭耦合颤振4个关键颤振导数[28]、、和的预测值决定系数均在0.980以上，MAE和RMSE值较低，尤其是与扭转分支耦合气动阻尼和非耦合气动阻尼相关的颤振导数和，其MAE和RMSE均低于0.05，且决定系数均在0.990左右，表明该模型所预测的颤振导数能直接应用到颤振计算当中.

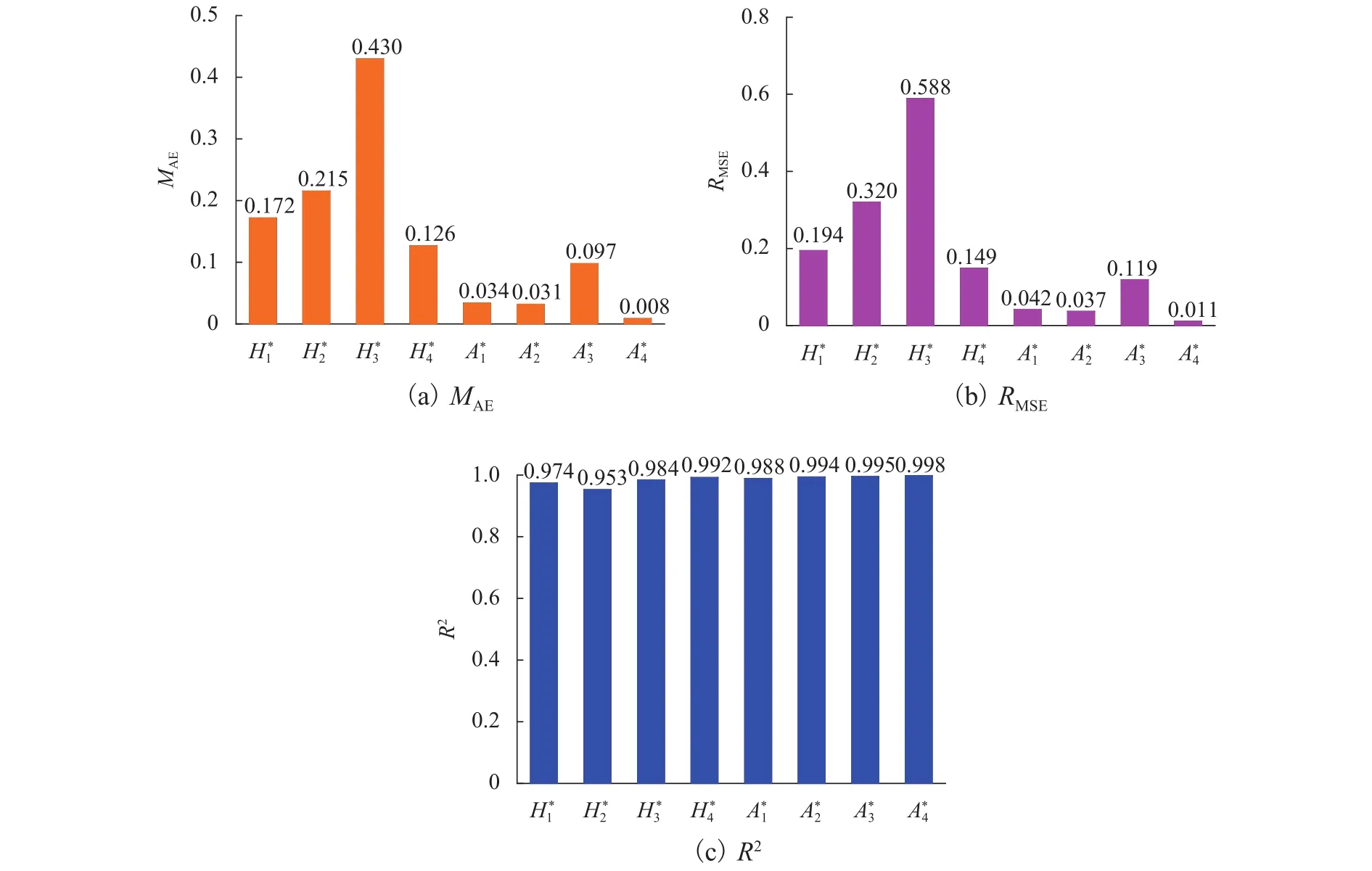
图10 测试断面颤振导数误差Fig.10 Error results of flutter derivatives of testing section

综合3种误差结果可以说明：本文所构建的集成式深度神经网络很好地学习到了断面形状特征与颤振导数的潜在关系，能够根据断面形状特性直接输出较高精度的8个颤振导数.

3.3 数据集大小的影响

事实上，众多神经网络的相关研究证实了数据集的大小对于模型的预测性能有较大的影响[24].一般来说，需要足够充足的训练样本才能显著改善模型的预测精度.为了研究本文所提出的集成式深度神经网络在处理数据量问题上的优势，分别按20%、40%、60%和80%的比例随机选取数据集（总数据量为510）作为模型的训练集，并利用训练完成的模型分别预测扁平箱梁的颤振导数.为综合评价不同模型的预测效果、便于展示，对8个颤振导数预测误差的3种评价结果求平均，如图11所示.

由图11可以看出：当训练集比例在60%时，预测结果精度已经较为理想；当训练集比例增加到80%时，其预测效果几乎接近于100%比例训练集；这一规律在3种评价指标上均有体现.

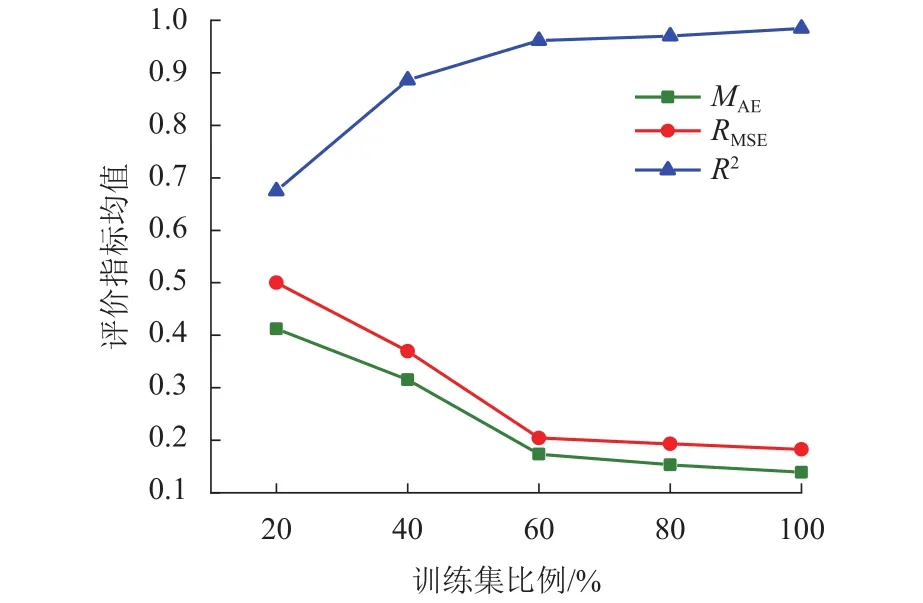
图11 训练集大小对误差结果的影响Fig.11 Effects of training set size on error results

本文提出的集成式深度神经网络的预测效果较好，利用较少的训练集即可达到较高的预测水平，这也说明了本方法对于数据的利用效率较高，且预测结果较为稳定，不存在欠拟合和过拟合问题.

3.4 不同模型预测的结果对比

本次研究的主要目标在于建立某种映射关系（或函数）R=f（x;δ） ，该映射关系的自变量x为扁平箱梁断面4个顶点坐标和1个折算风速，即，因变量R为 8 个颤振导数，即.通常，这种映射关系可利用显式的n次多项式回归模型进行实现，即利用上述数据集进行多项式系数拟合，构建非线性回归模型，如式（5）.

式中：xn为n次多项式展开的自变量，例如、yD、V2等，当n=2 时，xn包含 54 项，当n=3 时，xn包含219项； η 为回归系数矩阵； φ 为截距.

经测试：当n＞1 时，模型会陷入严重的过拟合状态，即训练集上的拟合性能较好，而在测试集上预测结果误差非常大；n=1时 ，即线性回归模型.利用最小二乘法和以上数据样本进行多项式回归模型拟合，得到的系数矩阵为

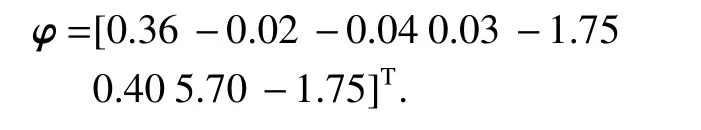
相较于本文提出的集成式神经网络模型，单个人工神经网络模型同样可以实现颤振导数的预测.构建与文献[11]相同的单一人工神经网络模型，该模型包含2层隐藏层，每个隐藏层包含20个隐藏神经元，激活函数选用 s igmoid.为对两种神经网络进行区别，此处的单一人工神经网络模型简称为“神经网络模型”.利用多项式回归模型和神经网络模型，对相同的测试断面进行颤振导数预测并进行误差评估，其结果与集成式深度神经网络模型预测结果之间的对比如表3所示（均值化）.

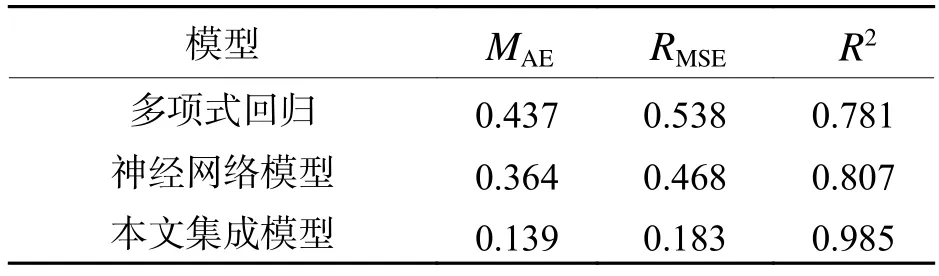
表3 误差结果对比Tab.3 Comparison of different errors

从表3中可以看出：1） 多项式回归模型获得预测结果的误差较大，对应的决定系数仅为0.781，不足以说明该模型的有效性.究其原因在于，在数据量较大的情况下，多项式回归模型易陷入严重的欠拟合状态，无法有效建立箱梁断面气动外形与颤振导数的关系.2） 对于单个神经网络预测模型，其预测性能优于多项式回归模型，但其MAE和RMSE误差高于本文提出的集成模型，且决定系数（R2=0.807 ）仅是略高于多项式回归模型，其有效性不足，无法应用到具体的颤振计算中.因此，本文提出的模型可以很好预测扁平箱梁的颤振导数.

4 结 论

本文的主要结论如下：

1） 提出了一种基于集成学习策略的深度神经网络模型.该模型能有效挖掘扁平箱梁形状特性，实现8个颤振导数的高精度预测.

2） 预测结果表明，仅利用60%的训练样本即可达到满意的预测精度，训练样本利用率较高.

3） 相较于传统的多项式回归模型和单个人工神经网络模型，本文提出的集成式神经网络模型的预测精度更高，可以应用到实际工程的颤振计算中.