PMSM新型积分快速终端滑模控制
诸德宏,周振飞
(江苏大学电气信息工程学院,江苏镇江 212013)
0 引言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)因结构简单、损耗低、功率密度高等优点在社会生产生活中受到广泛关注与应用,但PMSM 是一个非线性、强耦合的复杂电磁动作系统,在实际运行过程中往往会出现参数摄动、负载波动、外部干扰等问题。
传统PI 和滑模控制已无法满足当今工业社会日益增长的高性能控制需求[1-3]。随着现代控制理论的发展,国内外学者先后提出了许多优秀的控制方法。例如,自抗扰控制[4-6]、模糊控制[7-10]、滑模控制(Sliding Mode Control,SMC)等。
文献[11-13]提出一种新型的指数趋近律,通过克服常规滑模控制的固有抖振问题以提高趋近速度。Kang等[14]设计一种双幂次趋近率,改善系统在趋近模态中的动态品质。文献[15-16]设计滑模观测器采集PMSM 的转速与转子角度信息。张晓光等[17]提出混合非奇异终端滑模控制策略,结合线性滑模和非奇异终端滑模以解决非奇异终端滑模收敛速度慢的问题。周硕等[18]提出一种PMSM非奇异快速终端滑模控制(Nonsingular Fast Terminal SMC,NFTSMC)策略,能够全局快速收敛状态变量。李政等[19]通过在常规滑模面中加入状态变量的积分项,设计了一个PMSM 积分型滑模速度控制器,虽能消除稳态误差,但积分Windup 效应会使消除稳态误差的时间过长,系统性能有所下降。王鑫等[20]提出一种高阶积分滑模控制器,在减弱抖振现象的同时增强了系统的鲁棒性。
为进一步提高PMSM 调速系统的控制性能,本文提出新型积分快速终端滑模控制(New Integral FTSMC,NIFTSMC)方法。该方法在快速终端滑模控制的基础上引入积分型滑模控制思想,在继承快速终端滑模快速性的同时,通过重新设计积分项避免传统积分型滑模的积分Windup效应。
1 新型积分快速终端滑模控制策略
选用快速终端滑模面结合积分型滑模控制思想,将非线性函数与模糊量的积分形式引入滑模面,提出一种新型积分型快速终端滑模控制面,具体数学表达式如式(1)所示:
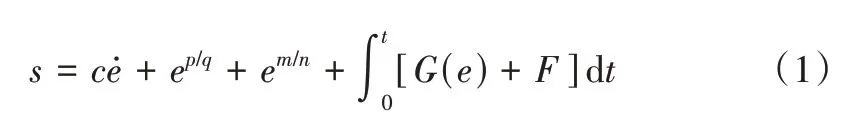
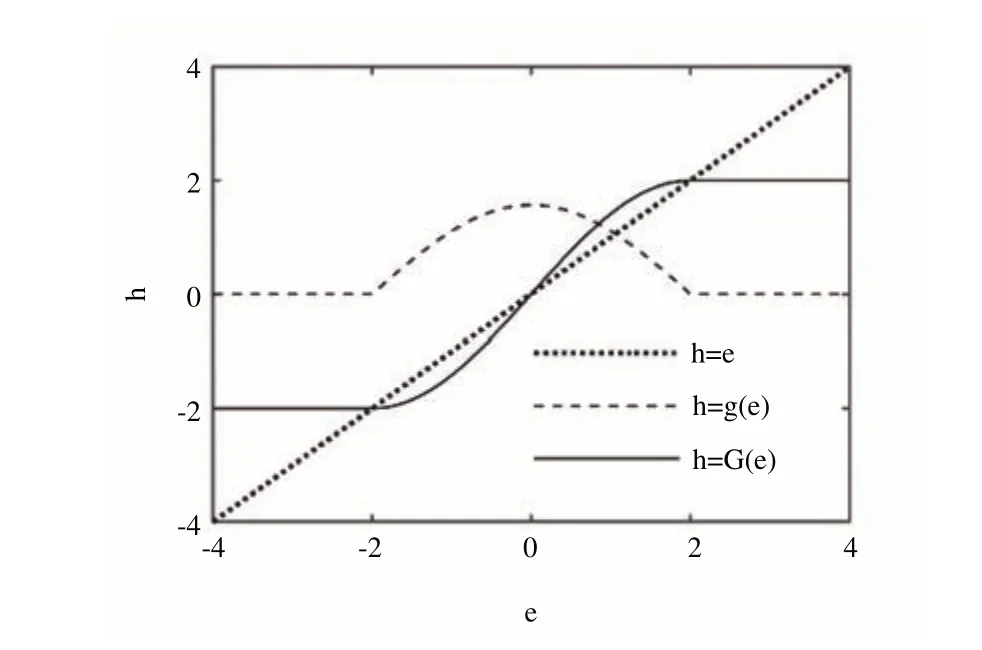
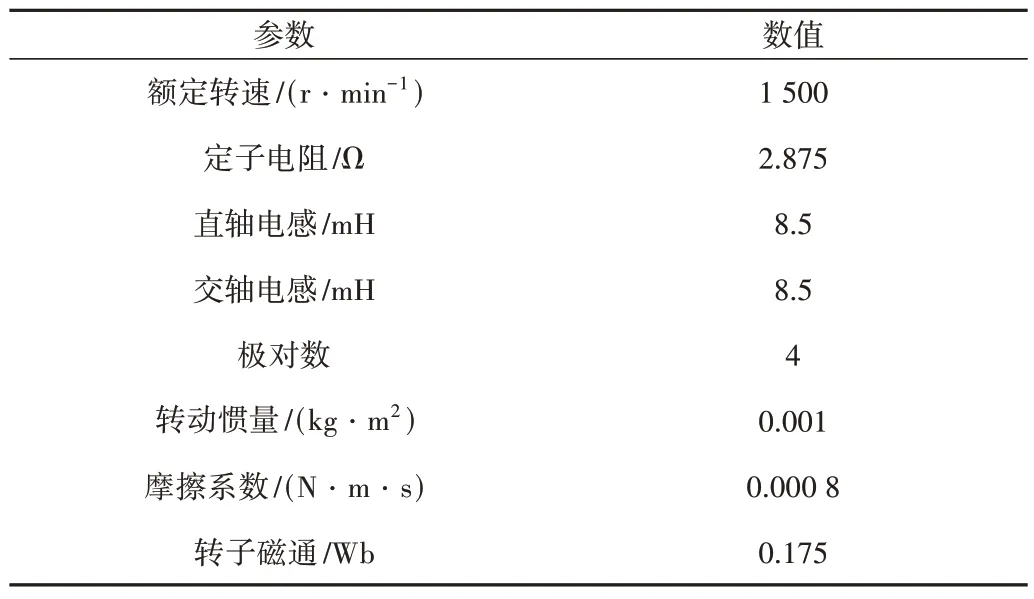
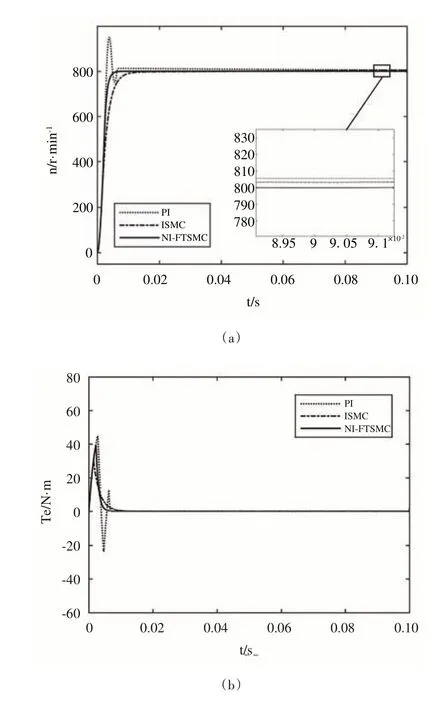
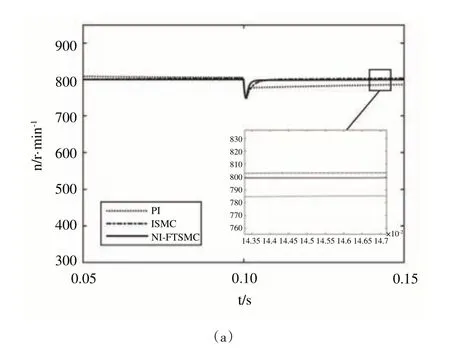
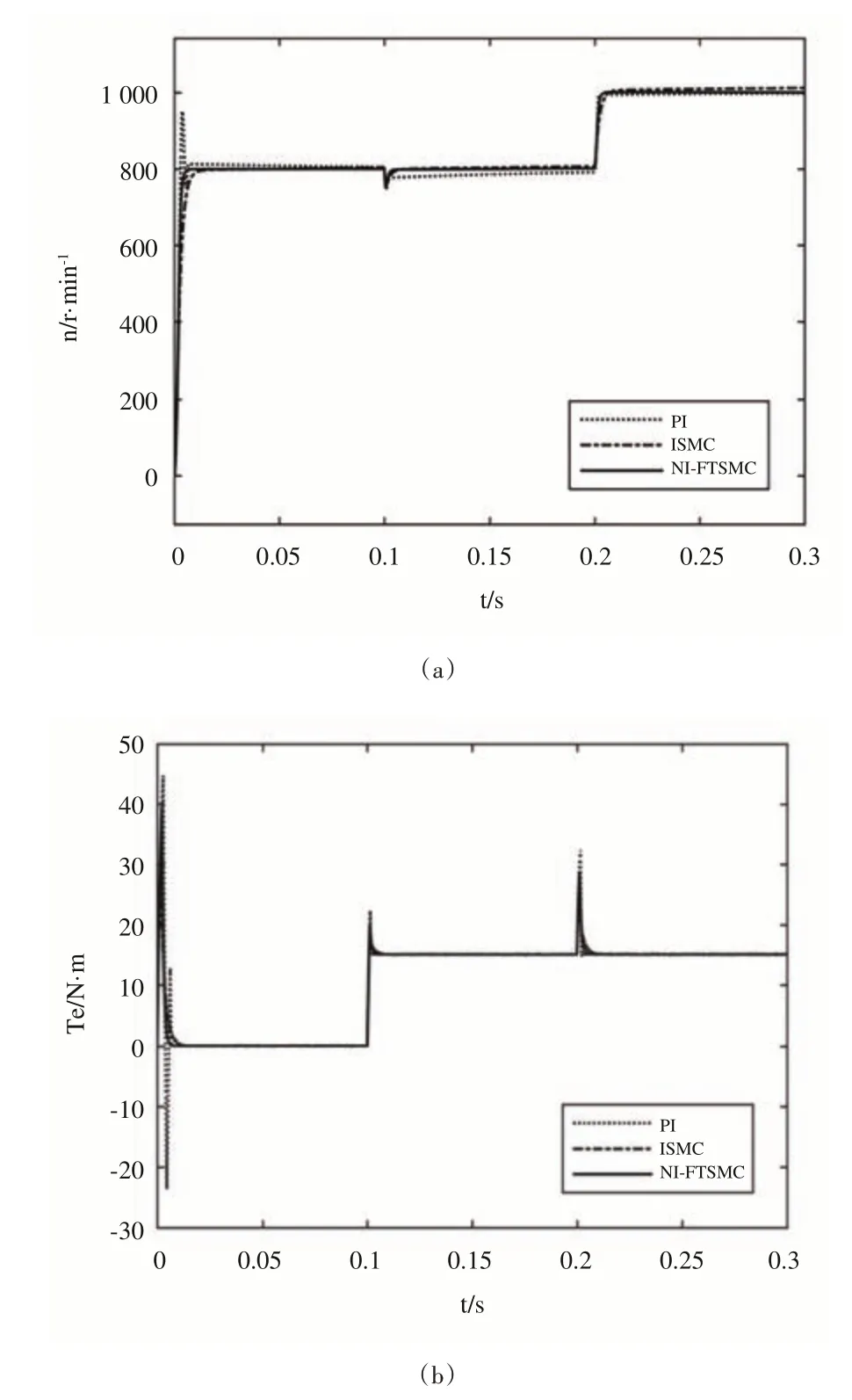
式中,c>0,p、q、m、n均为正奇数且0 如式(1)所示,滑模面由快速终端滑模和积分项两个部分组成。当s=0 且系统未到达平衡点时,快速终端滑模部分起主要作用,使e快速收敛;当系统接近平衡点时积分项部分起消除稳态误差作用。其中,G(e)是一类有界非线性光滑函数,可对积分起到减小系统稳态误差的作用。为了对G(e)进行分析,首先引入以下函数: 其中,g(e)是一类中间高两边低的连续函数,对G(e)积分具有放大小误差的作用,在大误差处锁定被积函数G(e)值的优点,可有效避免传统积分滑模Windup 效应。G(e)的计算公式如式(3): 当δ=γ=2时,G(e)、g(e)的函数图像如图1所示。 由图1 可见,当误差较小(即|e| ≤δ)时当误差较大(即|e| ≥δ)时饱和于±γ。通过调整δ和γ值,可实现所需要求的系统控制性能。 Fig.1 Nonlinear function and its derivative图1 非线性函数及其导数 由于积分项消除稳态误差存在一定滞后性,因此加入模糊量实现超前微调,通过模糊控制规则实时调整F值。 以表面式PMSM 为被控对象,在建立数学模型时做如下简化处理:①假设永磁体无阻尼,且气隙空间磁场正弦分布;②忽略铁心磁链饱和,不计涡流与磁滞损耗;③假设磁路线性,电感参数恒定。 因此,在d-q坐标系下PMSM 电压方程如下: PMSM 转矩方程为: PMSM 运动方程为: 其中,ud、uq为d、q轴电压,id、iq为d、q轴电流,Ld、Lq为d、q轴电感,R为定子电阻,np为电机极对数,wm为转子机械角速度,ψf为永磁体磁链,Te为电磁转矩,J为转动惯量,B为摩擦系数,TL为负载转矩,Ld=Lq。 设定系统状态变量为: 根据式(6)-式(8)进行求导,可得: 新型积分快速终端滑模面设计如下: 对式(10)进行求导得: 取趋近律为: 联立式(9)、式(11)和式(12)可得出PMSM 滑模速度控制器为: 接下来,进行系统稳定性分析,定义Lyapunov 方程为: 求导得: 根据Lyapunov 稳定性原理可知,该设计的滑模控制器能在任何初始情况下到达滑模面。 在积分项中加入模糊量实现超前微调,从而抑制由于积分作用引起的滞后效应。建立条件如下: (1)当x1与x2处于论域相反位置(包含中间位置Z0)时,此时的收敛处于正常状态,设F为Z0以减少干扰。 (2)当x1、x2均为正时,设F为正值;当x1、x2均为负时,设F为负值,控制x1的发散状态。 (3)当x1为正x2为负时,若x1绝对值较大,设F为正值,加快x1收敛;若x2绝对值较大,设F为负值防止过冲。 (4)当x1为负x2为正时,若x1绝对值较大,设F为负值,加快x1收敛;若x2绝对值较大,设F为正值防止过冲。 在滑移模态控制中,选取系统状态变量x1和x2为输入变量,F为输出变量,使用模糊推理法对输入、输出变量进行归一模糊化处理,记为其中,输入变量隶属度函数为Gusussmf类型,论域分别为[-3,3]、[-25,25];输出变量隶属度函数为Trapmf 类型,论域为[-18,18]。模糊控制规则设计如表1所示。 Table 1 Fuzzy control rules表1 模糊控制规则表 使用重心法对F进行解模糊计算,通过模糊规则建立的输入、输出3D 效果如图2所示。 Fig.2 3D renderings of fuzzy control system图2 模糊控制系统3D效果图 为验证本文所提出的控制策略的合理性及优越性,在MATLAB/Simulink 环境下搭建PMSM 调速系统仿真模型,采用id=0 的双闭环矢量控制方式。在转速环中将运用3种不同的控制器,分别为PI、传统积分型滑模控制器(ISMC)和新型积分快速终端滑模控制器(NI-FTSMC),电流环采用传统PI 控制器。系统结构框图如图3 所示。PMSM 参数如表2所示。 Fig.3 System structure framework图3 系统结构框架 Table 2 Parameters of PMSM表2 永磁同步电机参数 仿真实验的具体参数配置如下:仿真时间为0.3s,在转速800r · min-1下空载启动,运行0.1s 后突然增加15N ·m的负载,再过0.1s后将转速提升至1 000r · min-1。 空载启动后,3 种不同控制器控制下的系统动态响应结果如图4所示。 Fig.4 Dynamic response of the system at no-load startup图4 空载启动系统动态响应 由图4 可见,在空载启动阶段,PI 控制下的转速波形出现了严重的超调及波动;ISMC 控制下的转速调节时间较长,同时出现了转速误差;本文提出的NI-FTSMC 转速调节时间最短,且未产生超调和波动。 突加负载后,3 种不同控制器控制下的系统响应如图5所示。 Fig.5 System dynamic response when a sudden load is applied图5 突加负载下系统动态响应 由图5 可见,在突加负载的情况下,PI 控制下的转速无法迅速恢复到给定状态;ISMC 控制下的转速响应速度较慢,且误差依旧存在;而在NI-FTSMC 控制下的转速波形响应迅速,波动小,无超调,转速跟踪精准。 转速突变后,3 种不同控制器控制下的系统响应如图6所示。 Fig.6 Dynamic response of the system with a given speed change图6 给定转速突变系统动态响应 由图6 可见,当给定转速突变后,ISMC 发生了由积分作用累积造成的误差增大的结果,这意味着控制系统需要更长的时间消除误差;NI-FTSMC 显现出了在各种干扰情况下优越的控制性能。 3 种不同控制器控制下的系统总体运行结果如图7所示。 Fig.7 Overall operating results of the system图7 系统总体运行结果 由图7 可见,PI 控制下的转速和电磁转矩波形波动最为明显,同时转速难以稳定跟踪,效果最差;ISMC 在经历频繁干扰后,在积分累积作用下会出现误差增大的现象,干扰会造成消除误差的时间增长,系统抗扰性也随之变弱;NI-FTSMC 反应灵敏,未发生超调现象,而且能够稳定跟踪,动静态性能十分优越。 综上所述,本文所提出的NI-FTSMC 方法相较于PI 和传统积分型滑模控制器(ISMC)而言,性能更加优越。 本文通过结合积分型滑模控制的概念,基于快速终端滑模控制方法,在滑模面中引入改进积分项,在保留快速终端滑模控制优点的同时,相较于传统滑模面具有更快的收敛速度。 此外,将积分项设计为非线性函数加模糊量的形式,能够在有效消除稳态误差的同时,尽可能的避免积分Windup 效应,显著提高了系统的控制性能。 针对PMSM 矢量控制调速系统的特点,通过设计新型积分快速终端滑模速度控制器,并与传统PI 和积分型滑模控制器进行比较。实验结果表明,所设计的滑模控制器能够有效提高系统的调速性能,为改善PMSM 调速系统的动态品质提供了一种有效的方法,但该控制方式需要设定较多参数,仍然还有较大的改进空间。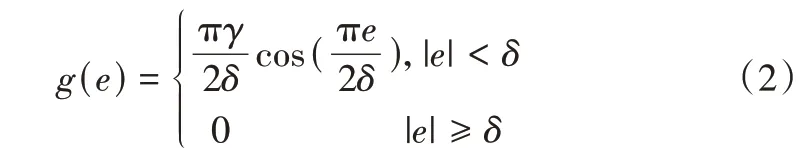

2 新型积分快速终端滑模控制器设计
2.1 PMSM 数学模型
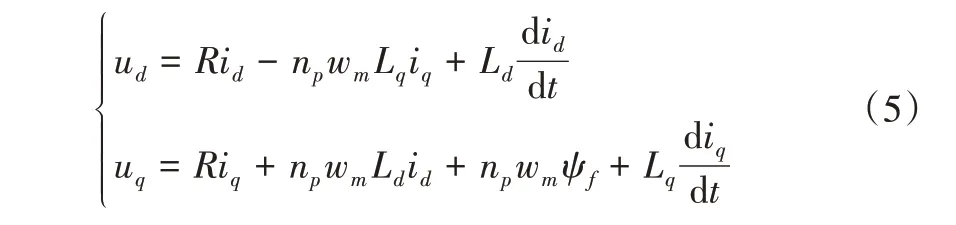

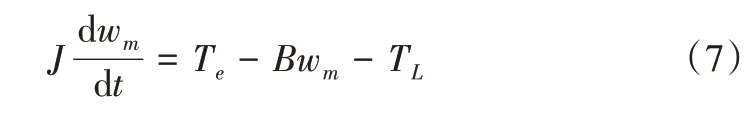
2.2 PMSM 滑模速度控制器
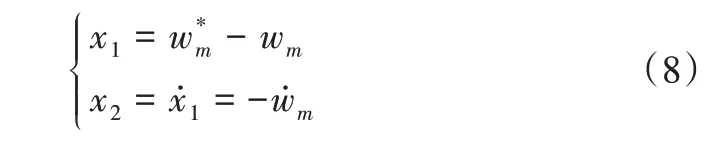

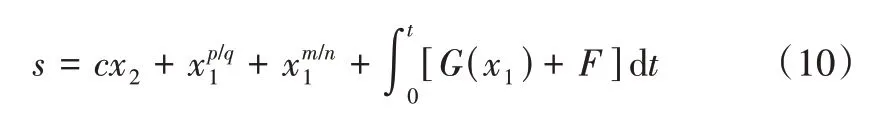
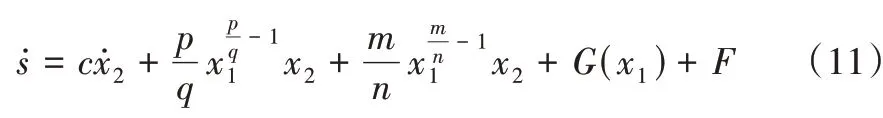
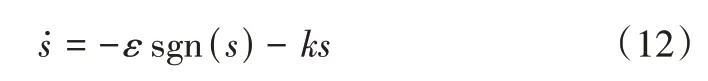



2.3 模糊控制器设计


3 仿真实验



4 结语

