改进鱼群算法在模拟机运动洗出优化中的应用①

王 辉, 阿迪娜

(中国民航大学 航空工程学院, 天津 300300)

六自由度运动平台作为一种并联Stewart平台, 是飞行模拟器的重要组成部分, 此外, 为了完成从真实运动轨迹到模拟信号的变换过程, 洗出算法成为了模拟与复现真实运动轨迹的重要环节之一.

经典洗出算法由Conrad等人[1]首次提出, 该算法具有参数设置容易、算法结构简单、运行性能稳定等特点, 所以该算法的被运用率一直都比较高. 但随着人们对模拟逼真度要求的提高, 经典洗出算法也暴露出了一些缺点, 如算法的洗出结果存在相位延迟、部分信号丢失、运动空间使用效率低下等问题. 因此, 为了获取更好地模拟效果, 许多研究人员对算法进行了优化研究. Parrish等人[2]基于连续最速下降法推导出了一种非线性的自适应滤波器, 协调了平移方向上的比力和旋转运动中的转速, 此外还设计了一种数字控制器以改善模拟平台的响应特征. 通过仿真发现运动的稳态幅度和相位响应都优于线性滤波器, 但由于定义代价函数时还需考虑针对不同情况下的成本权重, 因此导致计算量增大. 为了改善模拟器恢复到中立位置过程中的物理极限问题, 一种基于模糊控制逻辑和人体感知误差模型[3]的优化方法可以有效地改善经典洗出算法较为保守的问题, 并且能够为飞行员提供更好的感知效果. 之后, 随着进化算法的发展, Asadi等人[4,5]利用鲁棒性高且搜索可靠的遗传算法, 综合考虑包括倾斜协调时的人类感知阈值、平台运动极限等因素,设计了基于遗传算法的运动洗出算法. 该算法增强了人体对运动的感知, 改善了模拟平台对信号形状的跟踪, 还提高了对平台运动空间的使用效率. 郭盛等人[6]对洗出算法的结构进行了改进, 在原始洗出过程中增加了比例限制及频率限制环节, 从而使得模拟机运动平台不会产生运动超限的情况, 此外还提高了洗出算法运行的稳定性. 王辉等人[7]基于人体感知误差模型和模糊控制逻辑对滤波器的参数进行动态调节,再通过误差的补偿环节实现了对经典洗出算法中丢失信号的补偿效果, 通过仿真实验可以发现, 该改进方法可以较好地解决模拟逼真度不高的问题. 王辉等人[8]也采用了模糊补偿的思想对洗出算法进行改进, 其主要改进思想是利用补偿信号替代洗出算法中的低通滤波器, 从而提高模拟器的动感逼真度. 之后王辉等人[9]考虑到经典洗出算法中信号丢失严重, 提出了一种基于双路滤波校正的自适应洗出算法, 该算法通过不同信号分路合成补偿信号, 并借助自适应控制器实现对洗出位移的补偿和调目的, 仿真证明改进后的洗出算法对于相位延迟的问题有较明显的改善效果, 但是在运动信息的感知方面存在一些不足. 李炜增等人[10]基于运动误差模型和遗传算法对滤波器参数进行了寻优与优化, 通过该方法获得的滤波器参数可以保证算法在每次模拟过程中都可以获得足够的运动空间, 从而为下一次模拟运动做足准备, 同时改进后的算法在减少虚拟暗示方面也有较好的改善效果. 王辉等人[11]为改进经典洗出算法中信号丢失严重的问题, 结合人体感知模型对洗出算法的结构进行了再设计, 通过引入带通滤波器及自适应滤波器使得信号丢失及空间利用率等方面得到了明显改善, 但对于角速度的感知情况没有得到解决, 反而超出了人体的感知阈值. 刘伟超等人[12]在人体感知误差的基础上加入了对于平台运动余量的分析, 然后对截取到的丢失信号进行多重滤波并以自适应的比例情况再分别补偿到经典洗出算法的每一通道中, 从而实现对丢失信号的补偿, 最大程度地还原真实运动信号. 而新型仿生算法的产生给优化类问题带来了新的解决思路, 如李晓磊等人提出的人工鱼群算法(artificial fish swarm algorithm, AFSA)[13], 由于该算法具有鲁棒性强、参数设置简单、搜索能力强等优点, 因此被广泛运用于路径规划、参数寻优等多种问题中. 如文献[14]中利用AFSA对鲁棒PID的参数进行整定, 通过仿真结果可以发现, AFSA的寻优能力可以有效保证整定效果. 文献[15,16]也通过AFSA实现了对参数的优化, 并且仿真结果证明: 通过AFSA得到的新参数可以提高相应优化系统的运行性能. 但是,AFSA作为一种优化方法还是存在些许的不足之处, 需要提高全局搜索的能力以及算法寻优的精度. 张英杰等人[17]提出了一种基于动态调整人工鱼视野大小及拥挤度因子值的改进人工鱼群算法此外还引入了再寻优算子, 将改进后的算法代入到旅行商问题并分析其实验结果发现, 改进后的AFSA对于提高算法的寻优能力具有良好表现. 马宪民等人[18]提出的自适应视野的AFSA, 通过分析视野对于鱼群觅食行为的影响并进行改进后, 解决了基础人工鱼群算法中存在的算法后期收敛容易陷入局部最优值的问题. 为了能够实现更好的全局搜索效果, 刘东林等人[19]借助混沌变换实现了鱼群的初始化, 使得人工鱼的分布能够更加均匀且具有遍历性, 该思路对于优化群智能算法的来说十分具有参考价值.

基于上述对经典洗出改进方法的分析与总结, 本文提出了一种改进的人工鱼群算法, 即在基础AFSA中融入引力搜索算法(gravitational search algorithm,GSA)从而提高基础算法的收敛速度和求解精度, 更好地保证洗出结果具有良好的运动复现效果.

1 人工鱼群算法及其不足

AFSA算法的核心思想是: 水域环境中的鱼类会偏向于朝着食物浓度较高且拥挤度不高的位置聚集或觅食. 基于这一思想, 算法的行为可描述如下(见图1,以极大值问题为例)[13]:

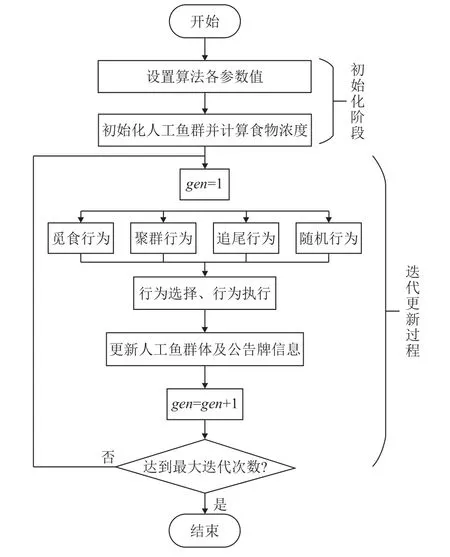
图1 基础人工鱼群算法执行流程

1) 觅食行为是指人工鱼个体在视野范围内搜索到某个食物浓度优于当前状态的位置时所采取的移动行为. 该行为的移动方式为:

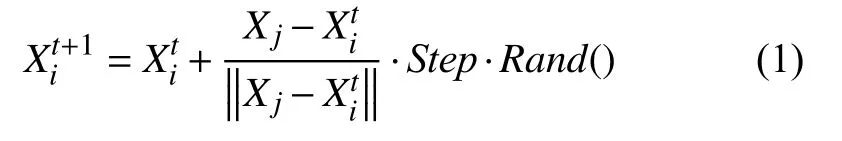
其中,为当前人工鱼所在位置,Xj为视野范围Visual内对应最优食物浓度的位置,Step为移动步长,Rand()是[ 0,1]内的随机数.

2)追尾和聚群行为分别向视野范围内食物浓度最高位置Xj和伙伴中心位置Xe移动的行为, 其移动方式分别如式(1)、式(2)所示.

3)如果经上述3种行为后, 人工鱼的探索次数达到尝试次数trynumber时, 算法仍然没有搜索到新的较优解, 则人工鱼将执行随机行为, 其移动方式如式(3)所示:

1.1 AFSA的不足

在AFSA中聚群行为与追尾行为主要负责向邻域内最优值处聚集, 觅食行为奠定了算法收敛的基础, 这几种行为使得AFSA具备了高效、稳定的全局寻优能力, 且对于多种优化问题都具备较强的适应性. 但是基础的AFSA也具有一定的不足, 如人工鱼在执行觅食为时若采用固定的步长对搜索空间进行探索和移动, 则有可能导致以下两种情况发生: 第一, 选择较大移动步长进行搜素时, 虽然加快了算法收敛的速度, 但当步长超过一定值后, 就会在算法迭代后期产生人工鱼个体在全局最优解处来回震荡的现象, 从而降低了算法的收敛速度. 第二, 假如选择较小步长进行搜索,虽然能够保证算法的搜索精度, 并且不会产生震荡现象, 但是较小的移动步长会导致算法在达到尝试次数时只对较小搜索空间进行了探索, 从而使得收敛速度减慢, 有时还可能导致人工鱼个体陷入局部最优值情况的发生.

由于算法在设置步长时存在的随机性使得算法寻优精度难以保证, 因此, 本文考虑一种能够改进人工鱼觅食行为中移动方式的方法, 以削弱因步长设置不合理而对算法迭代结果产生的不良影响.

2 改进的人工鱼群算法

2.1 引力搜索算法

引力搜索算法由Rashedi等人于2009年提出[20],它是一种可以针对所有优化问题实现最佳解决方案的启发式优化算法. 该算法基于万有引力定律和牛顿第二定律, 即“物体的加速度与其受到的作用力成正比,与其质量成反比”, “宇宙中每个粒子之间的相互引力都与其质量的乘积成正比, 与它们之间距离的平方成反比的力吸引所有其他粒子 ”.

对于一个优化问题来说, GSA的执行流程如下:

2) 在万有引力的作用下, 该空间内的所有粒子都将受到来自其他粒子的吸引力, 与此同时, 每一个粒子的质量大小与其适应度值的大小成正相关, 即: 粒子的质量越大其所处的位置就更优.

3) 所有粒子将遵循牛顿第二定律并沿着具有较大质量粒子的方向移动, 最终聚集在位置最优的粒子附近, 从而达到全局寻优的效果.

由表1的计算内容可知, 在引力搜索算法中, 人工鱼个体在每一次迭代获取的是本次迭代结果中的最优、最差适应度值, 而每一粒子的加速度与速度信息是基于当次迭代的全局环境以及自身的适应度信息得到的. 因此, GSA可以针对人工鱼觅食行为中的每一个体提供不同的移动信息, 这一信息除了具备移动的步长大小以外, 还具备了单次迭代中指向全局最优解的方向信息. 即, 借助GS算法可以有效地提高人工鱼群算法对全局环境的敏感度和收敛效率.

表1 引力搜索算法计算内容

2.2 改进人工鱼群算法

由于AFSA和GSA中的步长值及速度大小都表示个体在单位时长内移动的距离大小, 于是就有但是, 在GSA中运动个体的加速度大小受全局合力以及自身重力的影响, 因此GSA中的加速度和速度为矢量信息. 此外, 通过GSA的加速度计算公式和速度更新公式可以得出: 每一条人工鱼的速度信息存在个体差异性, 并且随着迭代的进行, 加速度的增量将逐渐减小,这可以弥补基础AFSA迭代后期出现的因步长过大而导致收敛震荡或搜索精度降低的不足.

于是, 基于GS算法的位置更新公式, 基础AFSA觅食行为中位置更新方式将改变为式(4)的形式:

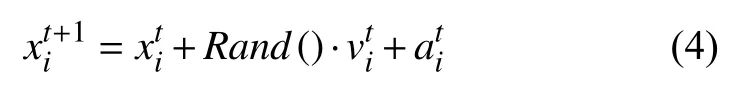
3 基于GSAFSA的洗出算法参数优化

3.1 洗出算法和建模

经典洗出算法由高通加速度通道、倾斜协调通道以及高通角速度通道组成, 如图2所示[1].

图2 经典洗出算法原理图

高通加速度通道利用三阶高通滤波器采集高频加速度信号, 经过一系列处理后输出模拟机运动平台的线位移信息. 其中, 高通加速度滤波器的传递函数表示如下:

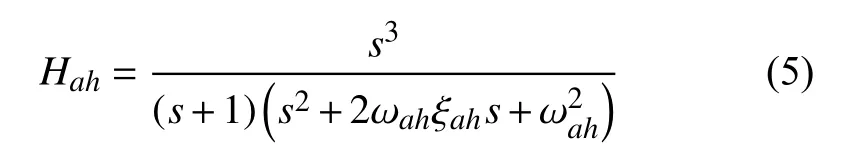
倾斜协调通道通过为运动平台提供一个较小的倾斜角, 从而实现对真实飞机持续加速运动模拟的效果.低通加速度滤波器的传递函数表示如下:

高通角速度通道负责对二阶高通角速度滤波器所洗出平台运动的姿态角信号进行处理, 从而得到平台运动的角位移信息. 其中, 高通角速度滤波器的传递函数表示如下:

3.2 建立目标函数

人体的前庭器官位于人耳的内耳之中, 包括感知线加速度的耳石, 以及感知角速度变化的半规管. 为了提高洗出算法的模拟效果, 减小人体对运动的感知误差, 因此以人体感知前庭系统为基础, 建立人体在不同运动方向上感知加速度和角速度的误差模型. 以x轴为例, 该模型的结构如图3.

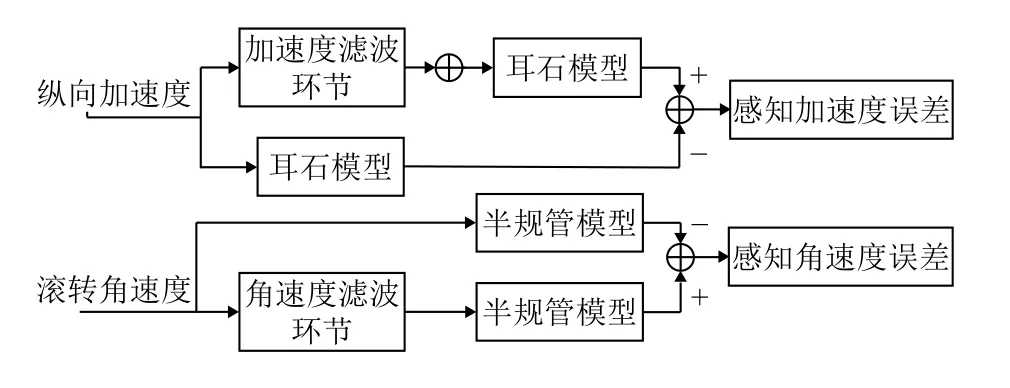
图3 纵向感知误差模型

该模型获取的是飞行员对实际运动状态的感知情况与对模拟运动状态的感知情况之间的误差, 包括感知加速度和感知角速度误差, 然后在此基础上建立以滤波器参数为自变量的目标函数. 以纵向(x方向)运动为例, 在该方向上的加速度感知误差函数和滚转角速度感知误差函数分别为:

其中,L[eax(t)]表 示加速度误差函数;L[ax(t)]表示纵向加速度的拉氏变换;Fhx(S)表示高通加速度通道滤波器传递函数;Flx(S)表示倾斜协调通道滤波器传递函数;G(S)0表示人体耳石模型的传递函数.

其中,L[ep(t)]表 示角速度误差函数;L[px(t)]表示滚转加速度的拉氏变换;Fhp(S)表示滚转角速度高通滤波器传递函数;G(S)v表示人体半规管模型的传递函数.

根据拉氏变换与傅里叶变换对上述两函数化简便可得[21]:

其中,x1、x2、x3分别对应高通加速度通道滤波器、高通角速度通道滤波器、倾斜协调通道滤波器传递函数的自然截止频率ωah、ωωh、 ωωl.x4为滤波器阻尼.

3.3 滤波器参数优化

优化前首先对算法的基本参数设置如下: 种群数目N=50 , 步长Step=0.1 , 视野Visual=1, 尝试次数Try_number=100 , 拥挤度因子δ =0.618, 最大迭代次数Genmax=50. 优化后结果见表2.

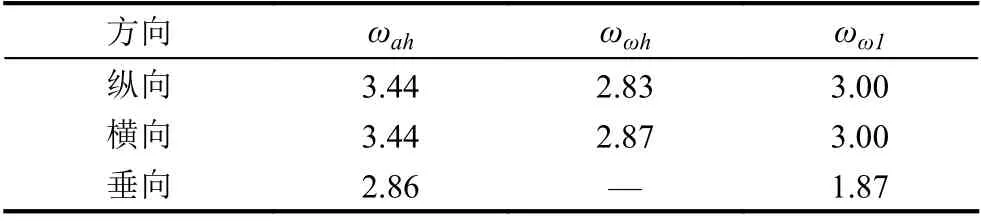
表2 优化后滤波器参数 (rad/s)

图4中红色曲线代表算法公告牌中记录的目标函数值, 黑色曲线表示的是算法在每一次迭代结束时获取到的最优值及其对应解, 而蓝色曲线代表上述两条曲线的差值. 由图可知, 改进后人工鱼群算法在第17次迭代时就搜索到了全局最优解, 且从第38次迭代开始波动逐渐减小. 所以, GSAFSA具有较快的收敛速度且寻优效果也较为稳定.

图4 算法收敛曲线

4 仿真与试验分析

4.1 仿真分析

为了验证GSAFSA的优化效果, 将新得到的一组滤波器参数放入在Simulink中建立的洗出算法仿真模型中, 并对实际的运动状态进行仿真模拟. 首先设置输入的加速度和角速度信号分别如图5、图6所示.

图5 输入加速度信号

图6 输入角速度信号

图7为3种洗出算法优化后的洗出位移, 其中, 经典洗出算法、AFSA改进的洗出算法和经GSAFSA改进的洗出算法洗出的位移极限值分别为0.055 m、0.027 m和0.019 m, 即经GSAFSA洗出的纵向线位移极限值最小. 这一结果表明, GSAFSA能够节约34%左右的运动空间, 即在运动的极限位置处, 经GSAFSA洗出的运动信号只需较小的运动空间就可以完成相同的飞行运动, 而节约下来的空间也可以用于之后的飞行模拟环节, 使模拟过程更加流畅. 同时, 在3种算法中, GSAFSA回归到初始状态所需时间更短, 这使得运动平台能够为下一次运动做充足准备. 图8经3种洗出算法洗出的纵向线加速度对比曲线. 由图可知, 相比于其他2种算法的洗出情况, 经GSAFSA洗出线加速度的恢复时间更符合输入信号的设置情况, 而且只需相对较少的时间就能够完成对线加速度的模拟过程,再一次证明了经GSAFSA改进后的洗出算法能够节约运动空间.

图7 洗出线位移对比

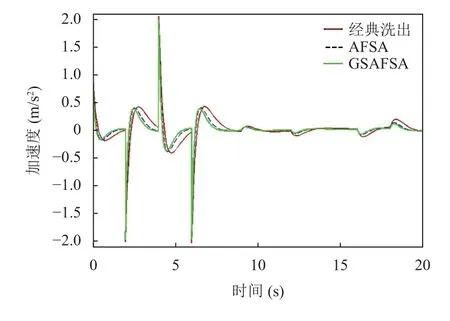
图8 洗出线加速度对比

图9所示的是人体对洗出线加速度的感知曲线,该曲线反映了模拟器驾驶员对于运动的感知情况. 通过对比可知, 虽然3种洗出算法的感知曲线都与实际感知曲线存在差异, 但是相比于其他两种算法, 改进后的洗出算法与实际感知曲线之间的误差减少了5%左右. 即经GSAFSA改进后的洗出算法减小感知误差的效果更好, 其感知曲线也更接近实际感知情况, 可在一定程度上降低因运动洗出造成的虚假暗示. 图10是经3种算法洗出的角位移对比曲线. 经计算, 3种洗出算法洗出的角速度都未超过人体感知门限的0.062 8 rad/s.其中, 经典洗出算法、AFSA改进的洗出算法和经GSAFSA改进的洗出算法洗出的角位移极限值分别为0.18 m、0.17 m和0.16 m. 即经GSAFSA的洗出结果满足感知阈值的要求基础上不会产生额外的错误暗示.

图9 感知加速度对比

图10 洗出角位移对比

4.2 实验分析

为了检验改进的滤波器参数在实际模拟平台中的运行效果, 对经典洗出算法还有经AFSA 和GSAFSA改进的洗出算法进行信号处理, 并应用于基于Lab VIEW语言开发的飞行模拟器运动试验平台中, 通过对六自由度运动平台的实时杆长情况的分析, 来验证改进算法的有效性. 同样地, 以纵向运动模拟信号为例,试验采用的输入信号为一段如图11所示的阶跃信号(在4 s时由0变为1.5 m/s2, 10 s时再由1.5 m/s2变为0).

图11 运动平台输入信号

图12所示的是经3种洗出算法洗出时, 六自由度运动平台中1、2号杆的实时杆长变化情况. 该两杆的初始杆长为71.8 mm, 而在经典洗出算法、AFSA洗出算法和GSAFSA洗出算法中杆长的极限长度分别为43.80 mm、47.94 mm和49.04 mm, 由此可知, 经GSAFSA改进后洗出算法的杆长变化曲线最接近到初始杆长. 在模拟结束后, 改进后的洗出算法能够保证液压杆以较快速度恢复到初始位置, 而在其他两种算法中, 液压杆恢复到中立位置的速度较慢, 甚至出现了反向加速运动. 所以, 试验再一次证明了相比于其他两种洗出算法, 改进后的AFSA算法能够达到优化滤波器参数的目的, 同时改进后的洗出算法可以更好地节约运动空间, 从而为之后的模拟运动做更为充足的准备.

图12 1、2号杆的杆长对比

5 结论

本文针对AFSA搜索精度不高以及收敛缓慢的问题, 提出了一种结合GSA的改进算法. 该算法充分利用了GSA的快速收敛能力以及对全局环境的敏感度,提高了基础AFSA的收敛速度以及全局寻优的能力,从而提高了算法的搜索精度. 通过仿真的结果也可以发现: 改进后算法的洗出结果相比于其他两种算法的结果来说, 在减小相位延迟和虚假暗示以及提高模拟逼真度和空间利用率等方面, 具有一定程度上的改进和优化效果. 但是针对人工鱼群算法的初始化分布还可以继续加以思考与研究, 以更大程度的提高算法搜索到全局性, 从而得到更好的运动感知效果.