碳中和目标下煤炭行业低碳发展演化博弈研究
王 伟
(西安科技大学 管理学院,陕西 西安 710054)
目前,学者们对碳中和目标下煤炭企业低碳发展研究方面进行了很多开拓性的工作[1-3]。谢和平[4]提出了中国煤炭行业发展三大机遇。陈浮[5]将煤炭行业实现碳中和分为三个阶段,根据不同阶段的阶段特点给出了不同的策略。康红普[6]从顶层制度安排、推进煤炭行业碳减排、提升煤炭产需平衡能力等方面给出了煤炭行业的发展建议。这些研究主要是从定性的角度来探讨碳中和目标下煤炭行业低碳发展过程中面临的问题和阻碍。在定量分析方面。Thorsten Burandt[7]等人将全球能源系统模型(GENeSYS)应用在德国能源系统当中,并引入相应的敏感性分析方法来研究能源低碳发展路径的主要影响因素。ZhijieJia[8]运用中国能源-环境-经济分析(CEEEA/CGE)模型,认为煤炭的替代过程应该是“前期税收,后期投资”。
上述研究大多从宏观角度分析碳中和目标下煤炭行业的低碳发展状况,从微观角度研究的很少。在进行这种分析时,博弈论是一种非常有效的工具[9],同时在现在绝大部分政-企博弈模型中选取的博弈主体为中央政府和企业,而忽略了中央政府与企业之间还有地方政府这一重要的博弈主体[10]。基于上述不足,本文构建了地方政府和煤炭企业之间的演化博弈模型,创新性的假设地方政府监管策略为积极监管或消极监管。最后通过仿真分析对结果进行验证,揭示了参与者策略的动态演化过程。同时,对关键参数进行了敏感性分析,揭示了如何使演化博弈更快速更平稳的达到完美稳定状态。
1 地方政府与煤炭企业演化博弈分析
1.1 模型假设
1)博弈双方为有限理性[11]。
2)博弈双方可以相互学习,通过观察对方的行为来不断修正错误来达到完善策略的目的,因为博弈双方很难一开始就选择最优策略来实现自身利益最大化[12]。
3)地方政府有“积极监管”和“消极监管”两种策略。选择“积极监管”的概率为x(0≤x≤1),选择“消极监管”的概率为1-x。
4)煤炭企业有“积极进行低碳生产(改进)”和“继续保持传统生产模式(不改进)”两种策略。选择“改进”的概率为y(0≤y≤1),选择“不改进的概率为1-y。
1.2 参数假设和模型构建
根据地方政府和煤炭企业之间产生的实际问题,本文定义了相关收益参数。当地方政府选择“积极监管”,煤炭企业选择“改进”时,由于在监管过程中需要消耗人力,物力等资源,假设地方政府的监管成本为Cg,同时,煤炭企业积极进行低碳生产会给地方政府带来潜在收益Eg。由于煤炭企业选择改进自身的生产模式,在改进过程中需要投入大量的成本,假设煤炭企业改进后的生产成本为C2,改进后产生的额外收益为E2。同时,考虑到如果只依靠煤炭企业自身的资金进行低碳改进会对煤炭企业产生较大的压力,地方政府会对积极进行改进的煤炭企业发放一定数量的补贴S。当地方政府选择“消极监管”,煤炭企业选择“不改进”时,由于煤炭企业继续保持高碳排放,政府必须要承担相应的环境处理成本Ch。煤炭企业继续保持传统生产模式下的成本和收益,分别为C1和E1。当政府选择“积极监管”,煤炭企业选择“不改进”时,地方政府会对煤炭企业进行相应的处罚,处罚力度为P。
根据参数假设建立博弈双方收益矩阵见表1。

表1 博弈双方收益矩阵
1.3 博弈模型演化稳定性分析
通过分析地方政府与煤炭企业双方演化博弈模型的收益矩阵,可以得到地方政府在采取“积极监管”和“消极监管”策略时的期望收益和平均收益为式(1)—式(3)。
ug1=y(Eg-Cg-S)+(1-y)(P-Cg-Ch)
(1)
ug2=-(1-y)Ch
(2)
煤炭企业在采取“改进”和“不改进”策略时的期望收益和平均收益为式(4)—式(6)。
um1=x(E1+E2+S-C2)+(1-x)(E1+E2-C2)
(4)
um2=x(E1-C1-P)+(1-x)(E1-C1)
(5)
根据上式可以得到地方政府在采取“积极监管”和煤炭企业采取“改进”策略时博弈双方行为策略的复制动态方程为式(7)、式(8)。
联立地方政府和煤炭企业的复制动态方程可以得到博弈双方的复制动态微分方程组为式(9)。
令式(8)和式(9)为0可以得到系统在平面上的5个局部均衡点,分别是:A(0,0),B(0,1),C(1,0),D(1,1)和E(a,b)。其中
因为系统局部均衡点不一定是演化稳定策略(ESS),但是ESS一定是局部均衡点。方程组(9)的雅可比矩阵为:
如果将系统局部均衡点带入雅可比矩阵满足以下两个条件,则说明该点就是演化稳定策略(ESS)[13]。
trJ=a11+a22<0;detJ=a11a22-a12a21>0
通过将均衡点带入雅可比矩阵算得各点对应行列式和迹的表达式见表2。

表2 局部均衡点对应雅可比矩阵的行列式和迹
为了方便讨论行列式和迹的符号,通过结合实际情况做出如下假设:①E2
结合上述假设,有四种情景下的演化稳定策略需要被分析。
1)P
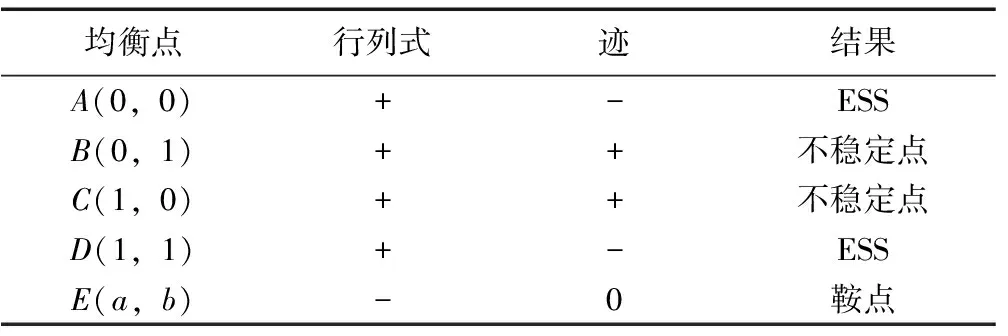
表3 情况1系统演化稳定结果
当演化博弈系统出现两种可能的均衡点时,最终系统稳定策略收敛于哪一个均衡点取决于系统初始状态[15]。当系统初始状态落在区域ABEC中时,系统稳定状态最终会收敛于点A(0,0),当初始状态落在区域ECBD中时,稳定状态最终会收敛于点D(1,1)。所以区域ECBD的面积越大,理想博弈结果发生的可能性就越大,区域ECBD的面积与鞍点E(a,b)有关。
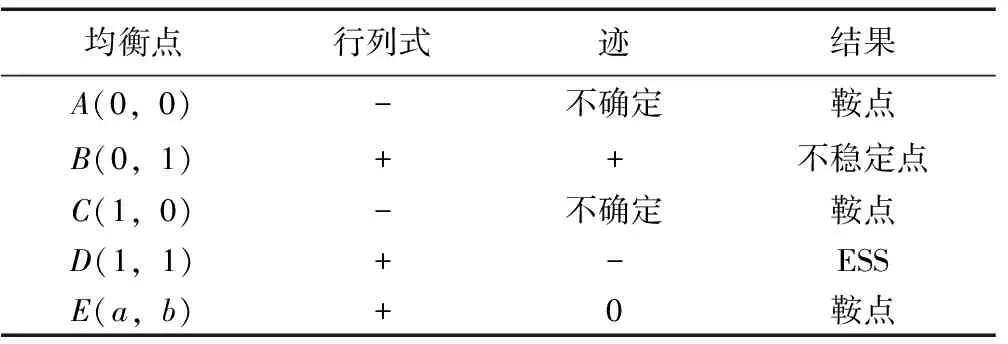
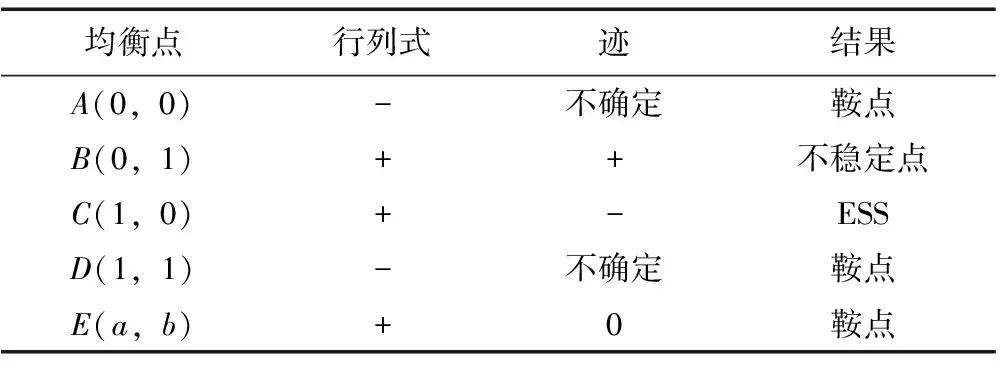
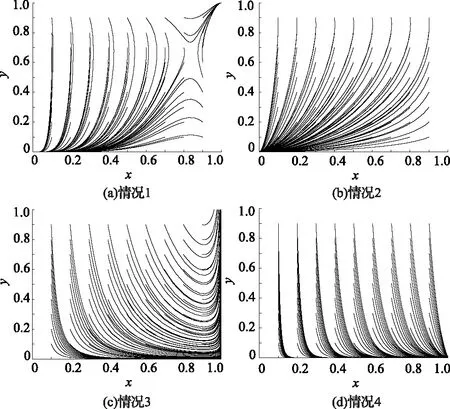
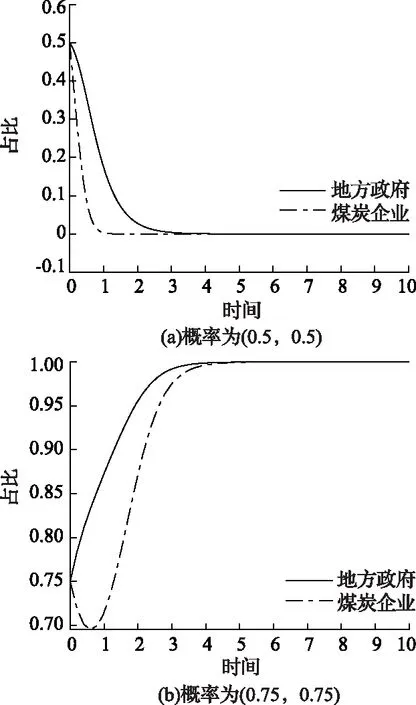
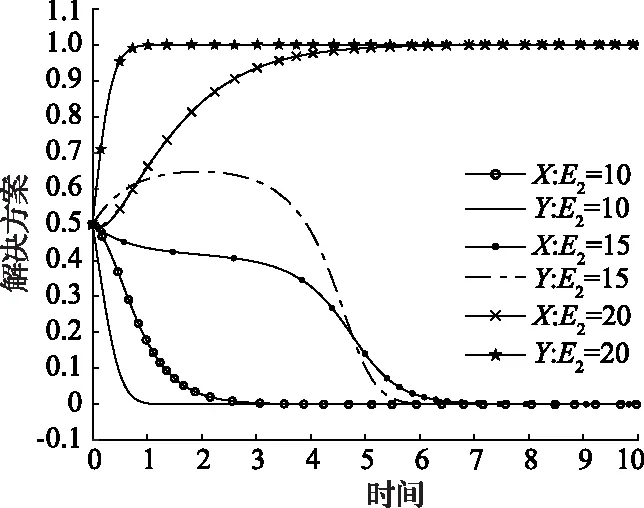
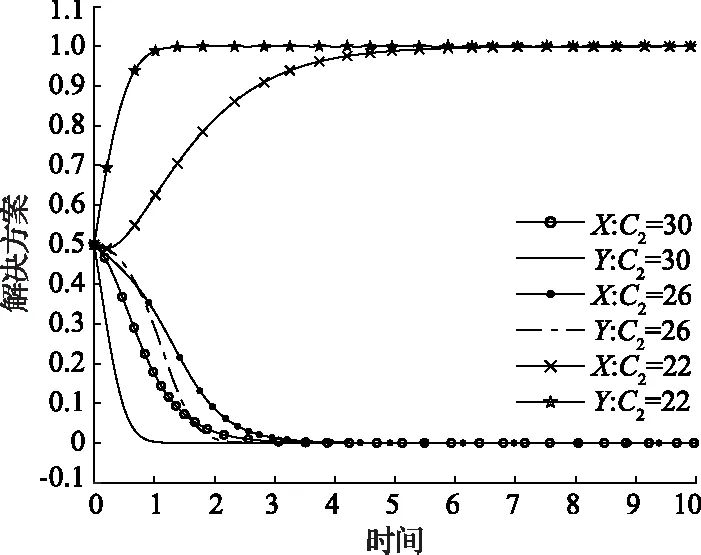
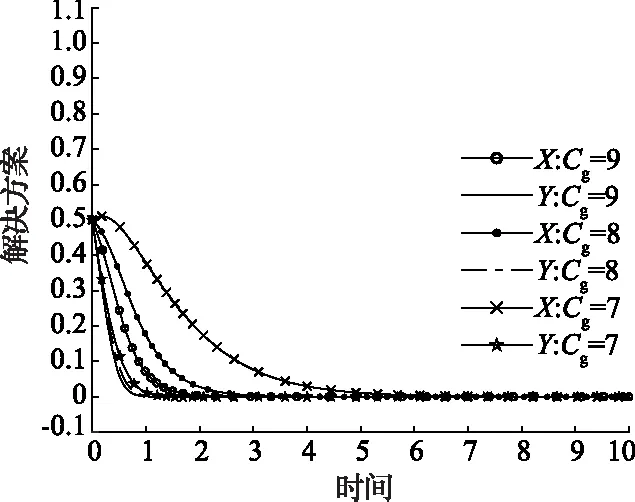
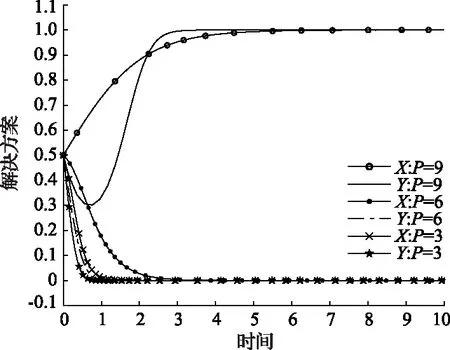
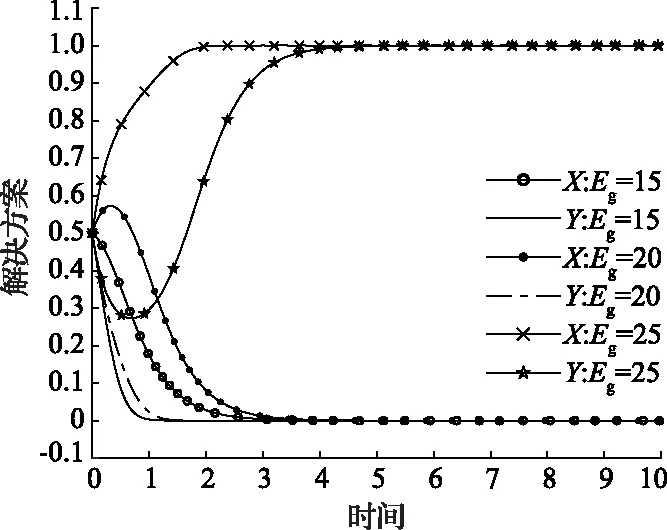
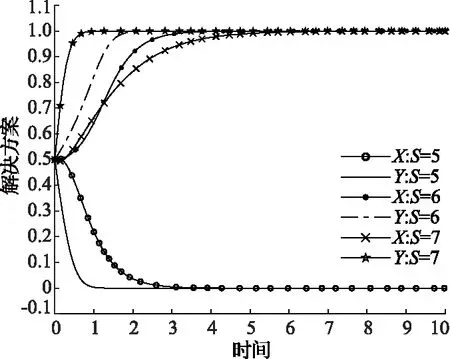
2)P 表4 情况2系统演化稳定结果 3)Eg 表5 情况3系统演化稳定结果 4)Eg 表6 情况4系统演化稳定结果 基于上述理论分析,借助约束条件和复制动态方程,运用Matlab软件对地方政府和煤炭企业的演化行为过程进行数值验证和分析[18]。相关参数设置如下,可以发现仿真结果符合上文分析。仿真结果如图1所示。 图1 情况1—4仿真结果 1)情况1:当参数取Eg=15;Cg=8;S=6;C2=30;C1=10;E2=10;P=6时,仿真结果如图1(a)所示,随着演化迭代次数增加,博弈双方选择(消极监管,不改进)和(积极监管,改进)策略组合的比例不断增加。 2)情况2:当参数取Eg=15;Cg=8;S=6;C2=30;C1=10;E2=10;P=2时,仿真结果如图1(b)所示,随着演化博弈迭代次数的增加,地方政府采取消极监管策略,煤炭企业采取不改进策略比例逐渐增大。 3)情况3:当参数取Eg=8;Cg=2;S=6;C2=30;C1=10;E2=10;P=5时,仿真结果如图1(c)所示,随着演化博弈迭代次数的增加,地方政府采取积极监管策略,煤炭企业采取改进策略比例逐渐增大。 4)情况4:当参数取Eg=8;Cg=2;S=6;C2=30;C1=10;E2=10;P=3时,仿真结果如图1(d)所示,随着演化博弈迭代次数的增加,地方政府采取积极监管策略,煤炭企业采取不改进策略比例逐渐增大。 上述四种情况的仿真结果都符合分析结果。 由上述分析结果和数值仿真结果可知,只有情况1和情况3条件下地方政府和煤炭企业的双方演化博弈系统会达到最优策略组合,即(积极监管,改进)。但是情况3下的最优策略组合是在地方政府重压情况下煤炭企业不得已的妥协行为,由于相关法律法规的不完善,情况3在实际情况中很难达到。所以在情况1的条件下,如何增加最优策略组合的概率就成了需要解决的问题。 首先分析博弈双方在不同的初始意愿状况下对演化结果的影响。假设博弈双方初始概率分别为(0.5,0.5)和(0.75,0.75),参数取值参照情况1,仿真结果如图2所示。可以发现,当地方政府选择“积极监管”策略,煤炭企业选择“不改进”策略的概率都为0.5时,系统最后的演化稳定策略组合为(消极监管,不改进);但当博弈双方初始策略选择的概率提升到0.75时,系统最终演化稳定策略组合变成理想策略组合(积极监管,改进)。根据上述分析可知,初始意愿状况会对演化结果造成影响,为了使系统最终演化稳定策略组合变成理想策略组合,有必要采取相应的措施,来提高政府主动积极监管和煤炭企业主动进行改进的可能性。这对减少煤炭企业碳排放,保证碳中和目标最终实现具有重要意义。 图2 不同初始概率下的仿真结果 为提高理想策略组合出现的概率,保证碳中和目标顺利实现,也可以通过改变系统主要参数的值来实现[19]。假设在情况1的数值模拟条件下,博弈双方初始概率为(0.5,0.5),在改变其他参数值的情况下其他参数值保持不变。 1)当煤炭企业进行低碳改进后额外的生产收益E2分别为10,15和20时博弈双方策略选择如图3所示。当E2=10,15时,博弈双方最终会选择(消极监管,不改进)策略组合,但是当E2增加到20时,博弈双方最终选择策略组合(积极监管,改进)。并且煤炭企业达到稳定所需要的时间比地方政府少很多。结果表明当煤炭企业可以获得令人满意的利润时,煤炭企业会主动选择进行技术改进。同时,煤炭企业的积极改进会给地方政府带来可观的潜在收益,政府也更加愿意去进行积极监管。 图3 E2的影响 2)当煤炭企业进行低碳改进后的生产成本C2分别为30,26和22时博弈双方策略选择如图4所示。当C2=30,26,博弈双方最终选择策略组合(消极监管,不改进),但是当C2降低到22时,博弈双方最终选择策略组合(积极监管,改进)。并且煤炭企业达到稳定所需要的时间比地方政府少很多。结果这表明当改进成本降低到可以接受的范围内时,煤炭企业会主动采取改进策略,同时随着改进成本的不断下降,演化达到稳定阶段所需的时间也在减少。 图4 C2的影响 3)当地方政府对煤炭企业监管成本Cg分别为7、8、9时博弈双方策略选择如图5所示。可以发现,不论Cg取何值,最终博弈双方的策略组合都会稳定在(消极监管,不改进)。但是随着地方政府监管成本的下降,达到稳定策略所需要的时间也在延长,这说明,虽然降低监管成本并不能达到最终理想的演化稳定策略,但是可以延长达到稳定状态的时间。在这个时间段内可以通过改善其他条件最终让地方政府会主动选择积极监管。因此采取必要措施降低政府监管成本是十分必要的。 图5 Cg的影响 4)当地方政府对不改进煤炭企业进行的惩罚P分别为3、6、9时博弈双方的策略选择如图6所示。可以发现,当P=3、6时博弈双方的策略组合稳定在(消极监管,不改进),当P值增加到9时,即惩罚金额大于监管成本后,博弈双方的策略组合最终稳定在(积极监管,改进),而且随着P值的增大,演化到稳定状态所需要的时间越短。即当地方政府对不改进煤炭企业的罚款金额小于政府的监管成本的时候,地方政府的监管积极性受到很大打击。同时,因为罚款金额较小,不能对煤炭企业产生震慑作用,煤炭企业在缴纳罚款过后的获得的收益仍然高于改进后所获得的收益,所以煤炭企业没有改进积极性。又由于相关法律法规的不完善,目前还不能对煤炭企业进行严格的惩罚,所以下一步地方政府可以继续完善相关的法律法规,提高惩罚强度,倒逼煤炭企业进行改进。 图6 P的影响 5)潜在收益Eg分别为15,20和25时博弈双方的策略选择如图7所示。可以发现,当潜在收益为15和20时博弈双方的策略组合最终稳定在(消极监管,不改进),同时随着收益金额的不断增加,地方政府演化曲线在开始有很明显的上扬,这说明地方政府的监管意愿不断增强。当潜在收益增加到25时,策略组合最终稳定在(积极监管,改进),这说明切实提高地方政府的潜在收益是提高地方政府监管积极性的必要手段,同时也可以为地方政府创造更多的社会公共效益和政治效益。 图7 Eg的影响 6)地方政府为煤炭企业提供的技术改进补贴S分别为5,6和7时博弈双方的策略选择如图8所示。可以发现,当S为5时,博弈双方的策略组合最终稳定在(消极监管,不改进),当S增加到6,7时,策略组合最终稳定在(积极监管,改进),并且随着补贴金额的增大,演化博弈系统达到稳定状态所需要的时间也越短。这说明当地方政府给予煤炭企业的技术改进补贴金额可以填补技术改进成本时,煤炭企业会更愿意主动的进行技术改进来减少生产过程的碳排放量。 图8 S的影响 本文研究结果表明博弈双方存在理想策略组合的可能性,即地方政府和煤炭企业分别选择“积极监管”和“改进”。并且这种可能性的大小取决于双方起始合作意愿的大小以及各种影响参数的大小。当降低监管成本或者提高潜在收益时,地方政府更愿意主动进行监管。当降低低碳技术改进成本或者地方政府给予相应的补贴和利好政策时,煤炭企业更愿意主动进行技术改进来进行低碳生产。达成理想策略组合有助于推动煤炭行业低碳发展,进而实现碳中和目标。结合研究结果,提出以下几点建议: 1)提高煤炭行业整体人才素质,加快技术研发进度,降低技术研发成本。煤炭企业是否愿意进行低碳改进主要取决于成本收益的大小。目前煤炭行业主要面临着原有技术碳排放量不达标,但是低碳技术研发采用成本过高的问题。为解决这一问题,煤炭行业应该积极与地方高校相合作,设置相应的交叉学科专业,加快“产学研”相融合,提高研发成果转化率。 2)完善相关激励和惩罚政策。政府应该从立法层面明确对煤炭企业的激励和惩罚。具体来说政府应该在财政预算的约束下加大对煤炭企业低碳改进的补贴力度,同时应该规定碳排放量测算标准,要求煤炭企业对其碳排放量进行及时披露,建立相应的考核标准,对于达到标准的企业进行奖励,对于不合格企业要加大处罚力度,倒逼煤炭企业及时进行技术改进。 3)地方政府积极拓宽监管渠道,降低监管成本。监管成本居高不下也是地方政府不愿意监管的一个重要原因,为此,地方政府要充分发挥群众、媒体和相关民间环保组织的力量,加大对碳中和政策的宣传。充分利用互联网,建立网络监管平台,让群众自发监管,通过这些举措可以为地方政府减少大量的监管成本。 4)大力开展煤炭行业第三产业的发展,提高煤炭行业收益。在煤炭企业开采完毕后,可以充分利用相关资源,大力发展旅游业,不仅可以借助旅游业来进行煤矿区生态修复改造,还可以带动周边群众以及煤炭企业下岗工人的再就业,同时提高煤炭企业收益,促进煤炭企业积极进行低碳技术改进。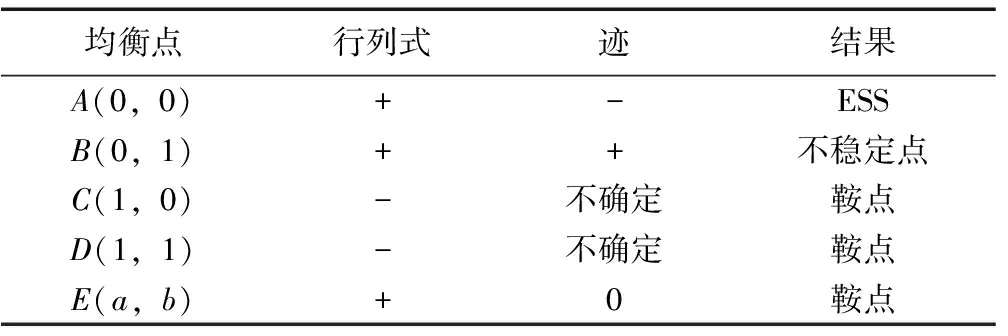
2 仿真设计及敏感性分析
2.1 不同情况下的稳定性结果仿真分析
2.2 双方参与主体初始意愿敏感性分析
2.3 系统主要参数敏感性分析
3 结论和政策建议

