基于巷道围岩预应力分布特征的锚杆支护参数研究

张庆国，赵红星，袁 爽，赵宝友

(1.山西三元煤业股份有限公司，山西 长治 046000；2.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

据统计，我国每年新掘进煤矿巷道总长达12000km，其中，超过80%的新掘巷道采用锚杆支护方式，并且这一比重将继续增加[1]。自1956年我国煤矿开始研究与应用锚杆支护技术以来，我国煤矿锚杆支护参数设计主要采用的理论包括国外学者提出的悬吊理论、组合梁理论、组合拱理论、最大水平应力理论等和国内学者提出的围岩松动圈理论、围岩强度强化理论、预应力锚杆支护理论、极限自稳平衡拱理论等[1-9]。锚杆支护理论最终的目的是在其适用条件下，设计出科学合理的锚杆支护参数，保障巷道安全的同时，提高生产效率，降低经济投入。为此，众多学者通过理论与实践相结合，不仅检验、修正、发展了锚杆支护理论，而且促进了我国煤矿的安全生产及锚杆支护技术的推广。例如：郑雨天和朱浮声1995年通过对国内外预应力锚杆应用进行总结后建议提高锚杆的预紧力和杆体的钢材强度[10]；陈庆敏等2002年通过对现有锚杆支护理论的总结，提出了基于高水平地应力的刚性梁理论和基于垂直地应力的刚性墙理论，并利用有限元数值模拟方法，给出了锚杆长度和预紧力的设计方法[11]；张国华等通过预应力锚杆加固层状顶板力学模型的理论解析，给出了直接顶范围内岩层间发生离层所必须满足的载荷、跨度、挠度3个条件和预应力锚杆的长度、间排距、预紧力关键支护参数的计算公式，并通过现场实践验证了锚杆支护参数确定的合理性[12]；刘玉田等针对高煤帮煤巷的稳定性控制问题，采用数值模拟方法对基于悬吊理论和组合梁理论确定的锚杆初设参数进行了优化，并通过现场应用检验了优化参数的有效性[13]；王洪涛等采用极限分析上限法，给出了防止巷道冒落破坏的锚杆支护预紧力计算公式[14]。

在煤矿锚杆支护实践中，人们早就认识到预应力对巷道围岩的主动支护作用[7，8，10，14-19]，即提高预紧力可增加锚杆支护效果。那么，在保证锚杆支护效果与安全条件下，可以通过适当提高锚杆的预紧力，放大锚杆的间排距，进而实现降低支护密度，提高掘支效率，减少投入的效果。因此，本文以山西三元煤业3号煤回采巷道为例，采用数值模拟方法，基于预应力在巷道围岩中分布规律，建立锚杆索预紧力与锚杆索间排距之间关系，为类似条件下巷道锚杆支护参数设计提供实用的理论参考依据。

1 工程概况

晋能控股山西三元煤业核定生产能力260万t/a，采用走向长壁综采低位放顶煤采煤法。现开采的3号煤层位于山西组下部，煤层厚6.36～7.5m，平均7.2m，普遍含0～2层炭质泥岩夹矸，结构简单，厚度大，属全区可采稳定煤层；煤层伪顶为厚0.1m的泥岩，直接顶为厚8.65m的砂质泥岩，基本顶为厚4.09m的中粒砂岩；煤层直接底为厚1m的泥岩，其下为厚2.98m的细粒砂岩；煤层埋深380～401m。

3号煤层4306工作面采用一进一回通风方式，进、回风巷道断面为矩形，毛宽5.2m，毛高3.5m，均沿煤层底板掘进，留有厚约3.7m的顶煤。基于悬吊理论和组合梁理论，设计锚杆索支护参数为：顶板锚杆型号为MSGLW-355/22×2400，每排布置5根锚杆，间距1.15m，靠帮距0.3m，排距1m，蝶形锚杆托盘规格为150mm×150mm×10mm，加长锚固长度不小于1.1m，预紧力矩250N·m，锚杆钢筋托梁型号为T4900×80/14-80×100；顶板锚索型号为SKP18.9-1/1860×8300，与锚杆按排间隔“2-2”布置，间距2.3m，排距1m，蝶形锚索托盘规格为300mm×300mm×14mm，端头锚固长度不小于1.75m；预紧力150～180kN；巷帮锚杆型号为MSGLW-355/22×2400，每排布置4根锚杆，间距1m，角锚杆距顶、底板分别为0.2m和0.3m，蝶形锚杆托盘规格为150mm×150mm×10mm，加长锚固长度不小于1.1m，预紧力矩250N·m，巷帮每排上两根锚杆钢筋托梁型号为T2300×80/14-80×100，下两根锚杆钢筋托梁型号为T1300×80/14-80×100。

2 锚杆索间排距数值模拟分析

2.1 数值计算模型

采用FLAC3D数值模拟软件，依据三元煤业3号煤层柱状信息，建立4306工作面回采巷道的数值计算模型，模型四周及底面均为面法向位移约束，煤岩层均采用拉剪复合破坏强度准则的理想弹塑性模型，主要煤岩层的物理力学参数见表1。

2.2 锚索预应力分布特征模拟分析

不同锚索预紧力下巷道顶板煤岩层预应力数值模拟结果如图1所示，由图1可知，随锚索预紧力P的增加，被单根锚索自由段夹持的煤岩层的预应力在锚索轴向逐渐贯通，且垂直锚索轴向的预应力影响半径RP随之增大；例如：当预紧力P=100kN，预应力阈值σP=0.015MPa时，预应力在煤岩体内分别以锚索自由段两端为长轴起点，沿锚索轴向的两个椭球体分布，且两椭球体在锚索自由段中部偏上位置开始叠加贯通，预应力影响半径RP=810mm；当锚索预紧力P增至150kN时，两预应力椭球体已大部分叠加，预应力影响半径RP=960mm；当预紧力P增至250kN时，两椭球体叠加为一个预应力椭球体，预应力影响半径RP=1250mm；当锚索预紧力或轴力为400kN时，预应力影响半径RP增至1610mm。预应力分布如图2所示，由图2可知，随锚索预紧力P的增加，预应力影响范围随之增大，只是其影响半径RP随预应力阈值σP的增大而减小。

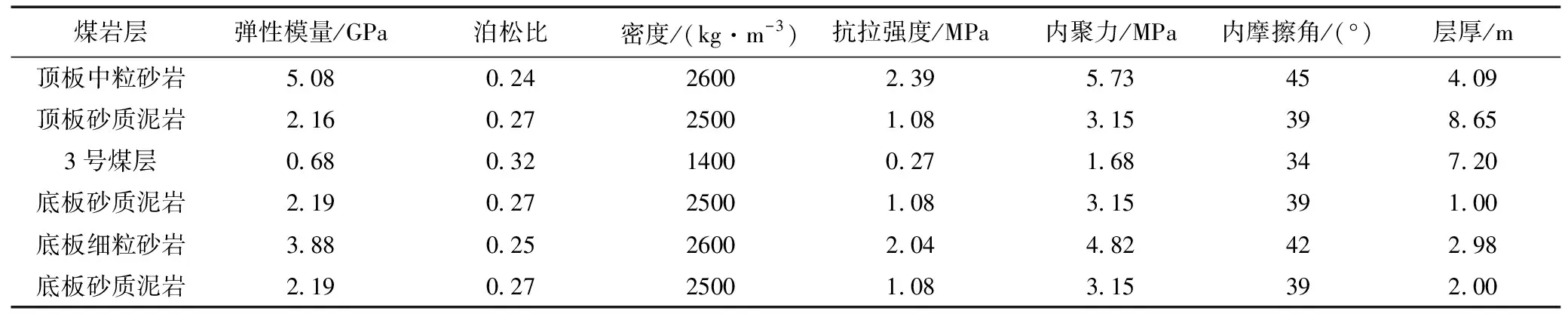
表1 煤岩层基本物理力学参数

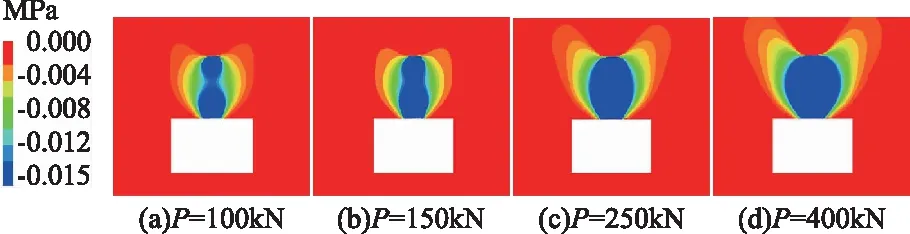
图1 不同锚索预紧力P下巷道围岩预应力分布 (σP≥0.015MPa)

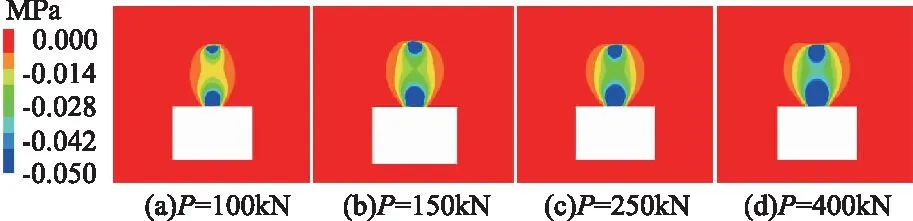
图2 不同锚索预紧力P下巷道围岩预应力分布 (σP≥0.05MPa)

不同锚索预紧力P下巷道围岩预应力分布云图如图3所示，由图3给出的预应力模拟结果表明，当锚索排距S=3m时，随锚索预紧力P的增大，单根锚索产生的预应力影响范围随之增大，最终相邻锚索间围岩的预应力产生叠加，在锚索自由段范围内形成连续加固拱效应；例如：若预应力阈值σP=0.015MPa，当预紧力P=100kN时，单根锚索产生的两椭球体预应力开始叠加，但相邻锚索间煤岩体的预应力未发生叠加；当预紧力P=200kN时，单根锚索产生的两预应力椭球体叠加为一个椭球体，且相邻锚索间煤岩体的预应力已发生叠加，预应力叠加高度约为锚索自由段长度的一半，基本形成连续的加固拱效应；当预紧力P=300kN时，单根锚索的预应力影响半径进一步增大，相邻锚索间煤岩体的预应力叠加高度约为锚索自由段长度的80%，相邻两锚索间预应力呈现苹果或扁鼓形状，已形成连续的加固拱效应；当锚索轴力或预紧力增至400kN时，扁鼓形预应力横向影响范围进一步增大。

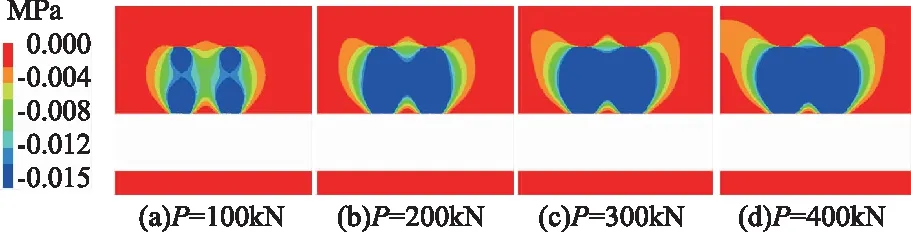
图3 不同锚索预紧力P下巷道围岩预应力分布 (S=3m，σP≥0.015MPa)

锚索预紧力为150kN、预应力阈值σP为0.015MPa，不同锚索排距下的预应力模拟结果如图4所示，从中可清晰地看出，当锚索排距较大时，如排距S为4m，相邻锚索间煤岩体的预应力基本未产生叠加现象；当排距S减小至某一值时，如排距S为3m，煤岩体预应力在相邻锚索正中间的锚索自由段一半位置处开始发生叠加，对比250kN预紧力单根锚索预应力影响半径为1250mm可知，相邻锚索间预应力叠加效应产生的预应力影响范围要大于单体锚索；当锚索排距S分别降至2m和1m时，相邻锚索产生的预紧力已充分叠加为苹果形状和扁鼓形状，加固拱效应显著。

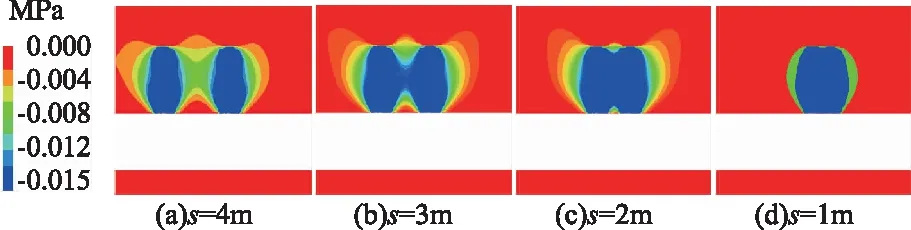
图4 不同锚索排距S下巷道围岩预应力分布 (P=150kN，σP≥0.015MPa)

为了确定锚索预紧力P、加固拱效应指标即预应力阈值σP和单根锚索预应力影响半径RP间的关系，对不同预紧力P和预应力阈值σP对应的预应力影响半径RP进行数理统计与拟合，获得了基于预应力分布特征下锚索支护参数确定方法的实用理论关系，如式(1)。由理论拟合公式(1)可知，锚索预应力影响范围RP与预紧力P和加固拱效应指标σP的负幂指数呈正相关。

式中，RP为单根锚索预应力影响半径，mm；P为锚索预紧力，kN；σP为锚索加固拱效应指标即预应力阈值，MPa。

锚索预紧力P、锚索加固拱效应指标σP和锚索预应力影响半径RP三者间关系的数值模拟结果和理论拟合公式结果见表2，从表中可定量地看出，上述理论拟合公式(1)计算得到的锚索预应力影响半径与数值模拟结果吻合较好，最大、最小和平均误差分别为11.16%、0.44%和2.19%。由此可见，上述理论拟合公式实用计算方法的精度可很好地满足煤矿巷道锚杆支护参数中预紧力P、间排距S(S=2RP)的设计要求。

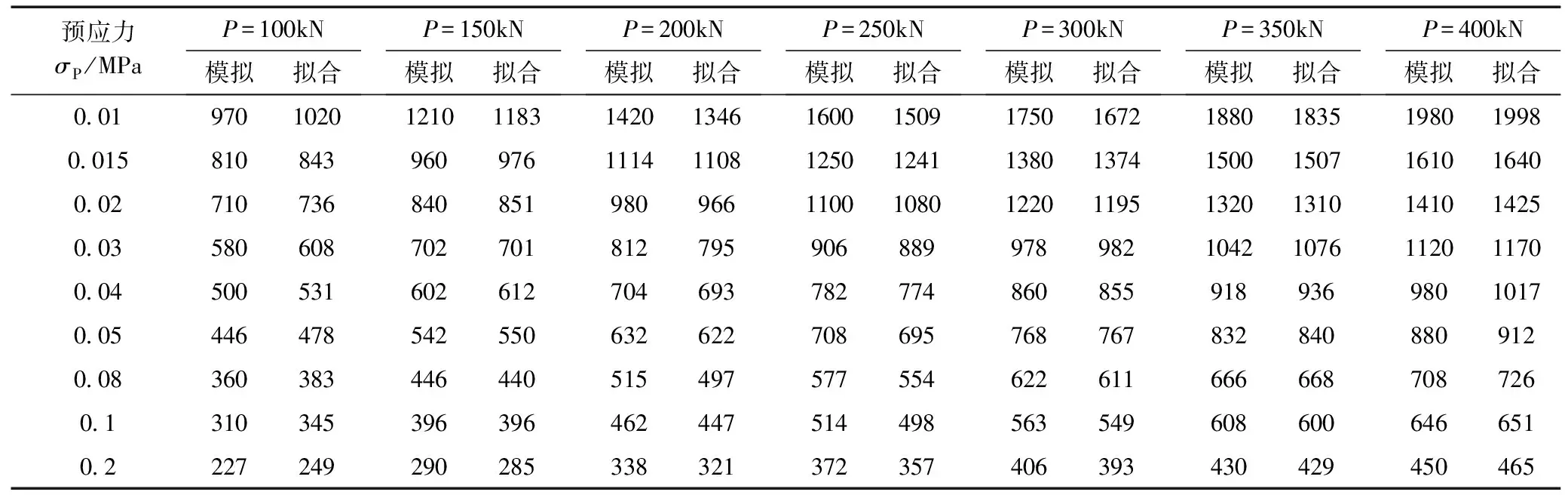
表2 不同锚索预紧力P及预应力阈值σP下预应力影响半径RP统计 mm

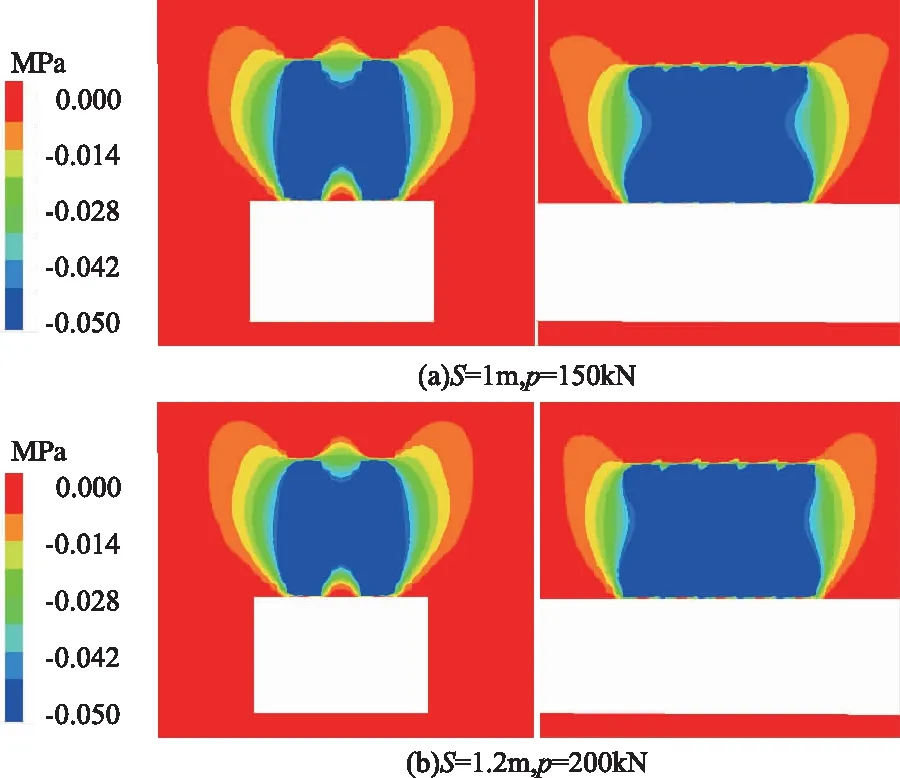
图5 不同锚索排距S下巷道围岩预应力分布 (σP≥0.05MPa)

三元煤业3号煤层回采巷道原顶板锚索支护参数和基于上述理论公式优化后的锚索支护参数下的预应力模拟结果如图5所示。从图中可直观地看出，若预应力阈值σP=0.05MPa，在间排距为2.3m×1.0m、预紧力150kN的原锚索支护参数下，回采巷道横纵断面的煤岩体在锚索自由段长度范围均形成了连续的加固拱，单体锚索影响半径至少为1.15m，如图5(a)所示，这与回采巷道能满足工作面正常回采的现场情况相印证；与图5(b)对比分析可知，锚索间距不变情况下，将锚索排距由1.0m增至1.2m，预紧力由150kN增至200kN后，回采巷道横纵断面也产生连续的加固拱现象，沿巷道走向纵断面的预应力影响范围增大，且横断面的预应力影响范围不仅未减小反而增大。由此可知，从煤岩体预应力分布特征角度来看，若增加锚索的间排距，可通过适当提高锚索预紧力，达到原高密度支护参数下相同的支护效果，进而实现低密度支护目的[8，10]。

2.3 锚杆预应力分布特征模拟分析

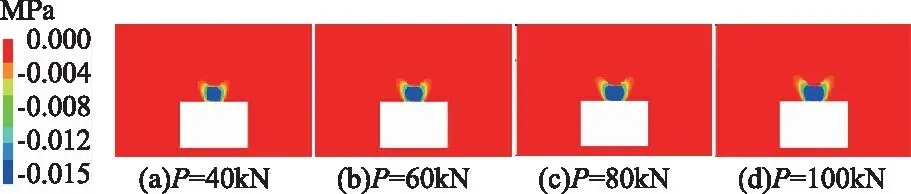
图6 不同锚杆预紧力P下巷道围岩预应力分布 (σP≥0.015MPa)

不同锚杆预紧力P下煤岩体预应力分布如图6所示，模拟结果表明，与不同锚索预紧力下煤岩体预应力分布特征一致，随锚杆预紧力P的增大，单体锚杆影响范围随之增大；例如：当预应力阈值σP=0.015MPa，锚杆预紧力P为40kN、60kN、80kN和100kN时，单体锚杆影响半径分别为505mm、633mm、733mm和870mm，煤岩体预应力沿锚杆自由段两端均呈现扁鼓形状。相同锚杆预紧力下，锚杆预应力阈值越大，预应力影响半径随之减小，在此不再逐一给出模拟结果。

不同锚杆排距S下煤岩体预应力分布如图7所示，模拟结果同样表明，与不同排距下锚索预应力分布特征相一致，当锚杆排距较大时，如排距S=3m，相邻锚杆间煤岩体的预应力不产生叠加现象；当排距S减小至某一值时，如排距S=1.5m，煤岩体预应力在相邻锚杆自由段一半位置处开始发生叠加，其预应力影响半径RP大于单体锚杆、大间距锚杆的预应力影响半径；当锚索排距S小于1.5m后，相邻锚杆产生的预紧力已充分叠加为一个扁鼓形状，加固拱效应显著。

锚杆预紧力P、预应力影响半径RP和加固拱效应指数σP三者的理论统计拟合关系形式与锚索的相同，如式(2)。

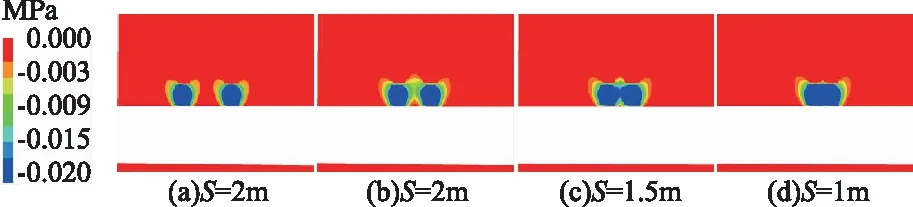
图7 不同锚杆排距S下巷道围岩预应力分布 (P=60kN，σP≥0.02MPa)

锚杆预应力预紧力P、锚杆加固拱效应指标σP和锚杆预应力影响半径RP的数值模拟结果和理论拟合公式结果见表3，误差分析表明：理论拟合公式实用计算方法最大误差为5.7%，最小误差为0.35%，平均误差为0.34%。由此可见，上述理论拟合公式(2)计算得到的锚杆预应力影响半径与数值模拟结果吻合较好。

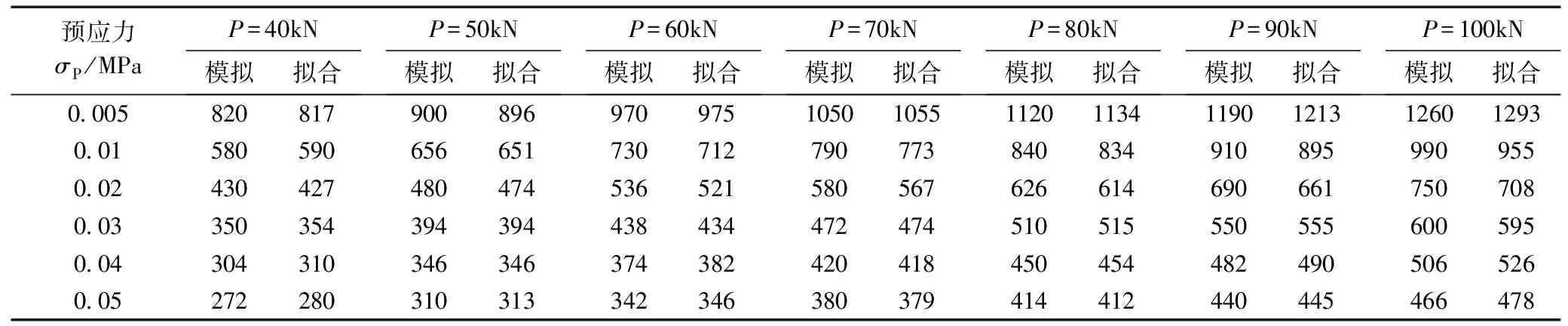
表3 不同锚杆预紧力P及预应力阈值σP下预应力影响半径RP统计 mm

不同锚杆排距S下巷道围岩预应力分布如图8所示。模拟结果表明，无论是间排距为1.15m×1.0m、预紧力60kN的原锚杆支护参数，还是锚杆排距由1.0m放大至1.2m、预紧力提高至75kN的优化支护参数，巷道围岩均形成厚度为锚杆自由段长度的连续加固拱，且优化后的预应力加固拱厚度略有增大。由此可见，也可以通过适当提高锚杆预紧力，来抵消锚杆排距放大带来加固拱效应降低的现象。

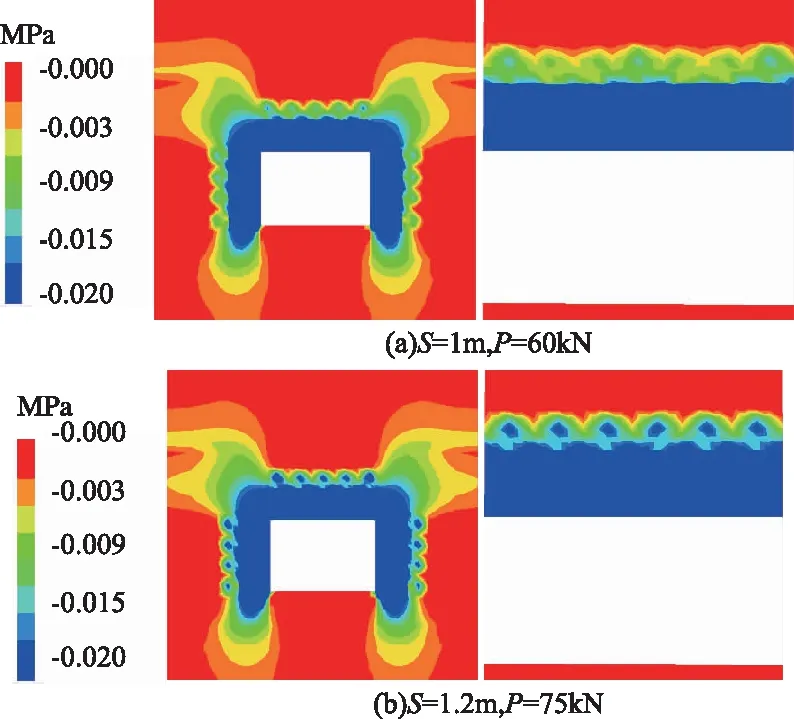
图8 不同锚杆排距S下巷道围岩预应力分布 (σP≥0.02MPa)

3 回采巷道锚杆支护参数优化及现场试验

3.1 锚杆支护参数优化设计

山西三元煤业3号煤层回采巷道锚杆预紧力一般为60kN，锚索预紧力一般为150～180kN左右。以往矿压监测信息表明，掘进期间巷道变形量较小，工作面回采动压作用下回采巷道未发生冒顶、溃帮和过大变形等影响工作面正常回采的现象，为此初步推断原锚杆支护参数有进一步优化的空间。锚杆支护参数优化的原则为锚杆索间距不变，放大其排距的同时，适当提高锚杆索的预紧力，以优化后的预应力加固拱效应不降低为评价指标，确定锚杆索的预紧力和排距。因此，基于上述优化原则，采用理论拟合公式计算得到原锚杆支护参数下的预应力阈值σP，并以此预应力阈值作为加固拱效应评价指标，再次利用理论拟合公式，计算得到排距放大后的锚杆索预紧力，最后采用数值模拟方法，对比分析优化前后巷道围岩的预应力分布，进一步验证理论优化结果的合理性和有效性。

将原回采巷道锚杆预紧力P=60kN、锚索预紧力P=150kN和锚杆索影响半径RP=500mm，代入式(1)和式(2)，计算得到锚杆和锚索的预应力阈值分别为σP≈0.02MPa和σP≈0.06MPa；依据该预应力阈值，可计算得到两种优化方案：方案一是锚杆索预紧力分别为65kN、200kN，排距1100mm；方案二是锚杆索预紧力分别为75kN、225kN，排距1200mm，其中排距S=2×RP。

由锚索悬吊理论可计算得到回采巷道锚杆索支护原方案、方案一、方案二的安全系数分别为1.83～2.00、1.66～1.82、1.52～1.67，其安全系数均满足设计要求。再考虑到实际锚杆索预紧力一般不低于其锚固力的40%～60%，确定方案二为最终的优化方案。

山西三元煤业3号煤层回采巷道优化前后的锚杆索预紧力和围岩预应力模拟结果如图9所示，对比分析可知：两种支护参数下回采巷道的两帮和顶板均形成了连续分布的加固拱，且锚杆索联合支护的顶板形成了低位锚杆加固拱和高位锚索加固拱叠加的加固拱效应；当回采巷道锚杆索排距由1m放大至1.2m后，由于锚杆索预紧力的提高，弥补了排距放大带来的加固拱支护效应下降的现象，且优化后的预应力影响范围不仅未减小还有所增加。由此可见，基于上述理论拟合公式计算得到的锚杆索支护参数在理论上是完全可行的。

3.2 现场试验效果分析

为验证上述基于预应力分布特征优化设计的锚杆索支护参数的合理性，选取距4306工作面切眼400～600m的200m运输巷作为试验段，其它地段仍采用原锚杆索支护方案。两种锚杆支护参数下4306运输巷的矿压信息统计结果分别见表4和表5。对比分析可知，与原方案相比，优化方案锚杆索的预紧力分别由57kN、151kN提高至76kN和228kN，使得运输巷掘进期间，无论是巷道顶板浅部离层、表面变形还是顶板深部变形均未超过原支护方案，且变形量较小，仅为20mm左右，说明高预紧力形成的较高预应力加固拱效应可较好地抑制掘巷期间围岩的变形；工作面回采期间受回采动压的影响，两种支护方案的顶板锚索轴力均增至310～320kN，顶板与巷帮的锚杆轴力均增至90～110kN，且均在锚杆索设计工作阻力范围内，优化方案下巷道顶板与两帮的变形与原方案基本一致，顶板浅部离层量为30～40mm，深部离层量为30mm左右，顶板下沉量约为110mm，两帮移近量为170～180mm，两种支护方案均未发生锚杆索破断、冒顶、溃帮和大变形等影响工作面正常回采的现象，验证了基于锚杆索预应力分布特征获得的实用理论公式优化设计锚杆索支护参数的合理性和有效性。

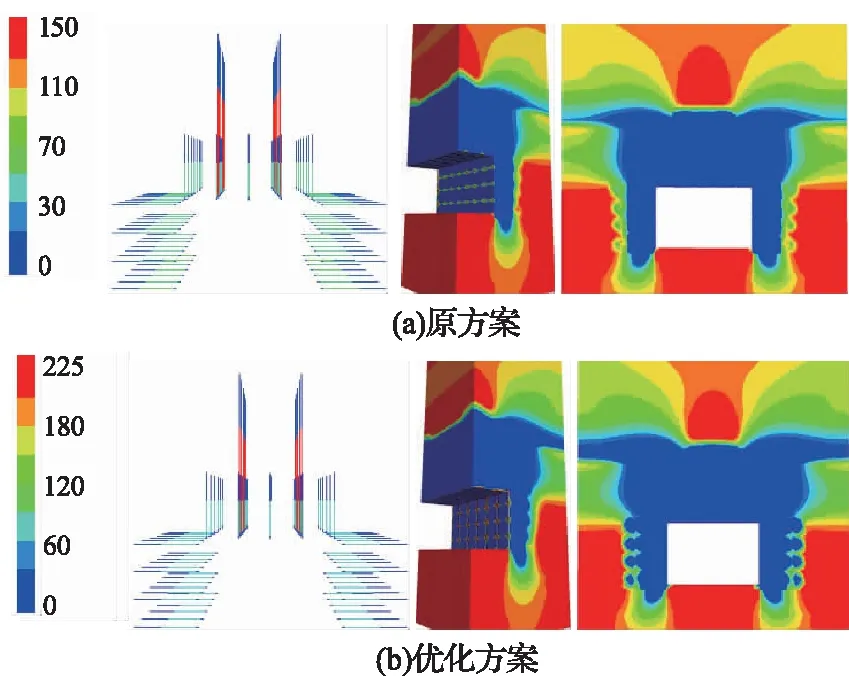
图9 回采巷道优化前后的巷道围岩预应力(kN) (σP≥0.02MPa)

表4 锚杆索轴力统计 kN

表5 巷道围岩变形量统计 mm

由此可知，回采巷道锚杆支护优化方案不仅提高了巷道的掘支效率，还降低了巷道掘支材料和人力的投入；掘支效率提高率、支护材料和人力投入节省率均超过20%以上，达到了低密度支护目标，提产增效显著，为类似条件下煤矿锚杆支护参数设计提供了可借鉴的实用理论计算方法。

4 结 论

1)预应力在巷道围岩内形成以锚杆索自由段为起点的预应力椭球体，随锚杆索预紧力的增加，单根锚杆索影响范围随之增大；当预应力增加到一定量值，相邻锚杆索的预应力椭球体将相互叠加，在巷道顶板及两帮形成“深度约为锚杆自由段长度的低位锚杆加固拱和深度约为锚索自由段长度的高位锚索加固拱”。

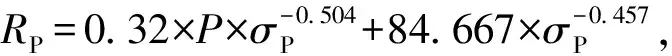
3)基于拟合得到的实用理论公式，优化设计了三元煤业3号煤层回采巷道的锚杆索支护参数；数值模拟和现场工业试验结果表明，优化前后的回采巷道在掘进及工作面回采期间，无论是锚杆索工作阻力，还是巷道围岩的深浅部离层和表面位移，均相差不大，未发生影响工作面正常生产的事件，验证了实用理论公式设计锚杆支护参数的合理性和有效性。

4)相比原锚杆索支护方案，优化方案提高了回采巷道的掘支效率，降低了巷道掘支材料和人力的投入，达到了低密度支护目标，提产增效显著，为类似条件下煤矿锚杆支护参数设计提供了可借鉴的实用理论计算方法。