基于EMD-SE-LSTM模型的股指日内已实现波动率预测——以中证500指数为例

刘 传， 陈彦晖

(上海海事大学 经济管理学院， 上海 201306)

随着中国金融市场的蓬勃发展，作为金融市场中重要组成部分的股票市场逐渐成为企业融资者筹集资金的重要渠道，同时也给投资者进行资金管理和实现投资收益提供了重要途径。在股票市场中，股票价格指数作为整个股票市场的股票总指数，反映了整体股票价格水平以及整体走势。股指波动率像是一个方向标，在波动的股市当中起着重要的作用。在即将遇到风险时，投资者利用股指期货将其对整个股票市场价格指数的预期风险转移至期货市场，以此来规避风险。股指期货也是对股票未来价格预期，深受股票指数的影响。股指期货的基础标的是股票指数。股指的波动率情况则是对股指未来走势的影响因素。而股票价格波动变化极其复杂，并没有明确的规律。因此，准确地预测股指的波动率及走势不仅可以有效地实现高额的投资回报还可以有效地规避投资风险。

股票指数的波动性是极其复杂没有明确规律的，想要从复杂的股指波动中洞悉股票指数的走势和波动情况，从而实现高额的投资回报，一直以来是人们关注的焦点问题。而股票指数数据具有非线性、不平稳、数据量很大、非常复杂等特点，增加了预测难度。而传统的预测金融数据模型则要求数据必须是平稳的、线性或近似线的，在预测股指走势和波动方面，其准确性和精度并不高。众所周知，经验模态分解是一种自适应性强的时间序列数据分解算法，能够对非线性、非平稳的时间序列数据进行分解，非常适合对像股指波动率这样的金融高频数据进行分解。面对庞大的金融时间序列数据，深度学习算法脱颖而出，它可以从大量复杂的数据中提取特征，无须依赖先验知识，非常适合预测高频金融时间序列的波动率，在所有深度学习算法中，长短期记忆神经网络因其循环结构和链状结构，具有长记忆性，可作为复杂的非线性单元构造更大型的神经网络。因此，长短期记忆神经网络更适合预测金额高频时间序列数据。

国内外对波动率的研究可以追溯到1982年，Engle提出并采用自回归条件异方差(ARCH)模型对金融资产收益率方差进行统计并有效地拟合了收益率的波动性，研究发现金融资产波动率具有高度的相关性[1]。随后其他传统模型也被纷纷应用于股指波动率预测，如ARMA模型、ARIMA模型、GARCH模型以及由GARCH模型改进的TGARCH、EGARCH、IGARCH等诸多GARCH族模型[2-5]。而后随着计算机技术的飞速发展，机器学习、深度学习等算法逐渐应用于高频金融时间序列数据分析当中。Ghosh等采用随机森林和LSTM网络作为训练方法对标普500指数成分股进行预测，结果表明，使用LSTM网络的多特征设置提供了0.64%的日回报要高于随机森林0.54%的日回报[6]。杨青和王晨慰在研究全球股票指数预测中，实证表明LSTM神经网络具有很强的泛化能力，预测效果非常稳定，与其他模型对比，LSTM模型预测精度很高且能够有效控制误差[7]。 Zhang等使用长短期记忆网络模型来预测股价走势，通过采用投资者注意力的代理变量作为市场变量的补充，实证结果表明，LSTM模型相比其他的人工神经网络(ANNs)在处理非线性、非平稳和复杂的金融时间序列更合适，且其预测精度更高[8]。而经验模态分解将时间序列数据根据自身的时间尺度特征分解成不同周期、不同频率的本征模函数和残差项，无须提前设定任何基函数，也不要求数据是线性、平稳的。刘海飞和李心丹使用EMD分解算法对股票价格进行预测和小波分析预测方法做比较，实证研究表明，使用经验模态分解方法预测结果精度更高、拟合度更优、预测功能更强、模型更加稳定[9]。 Luo等通过构建EMD-Copula-CoVaR模型来衡量国际股票市场多尺度的金融风险传染力，实证结果表明，EMD-Copula-CoVaR模型在衡量金融风险传染在所有时间尺度上都是有效的，金融风险传染主要贡献者是高频成分。同时还实证了除英国外，在原始和中频分量下，美国金融市场对其他金融市场输出的风险要高于接受的风险[10]。Wei等为了能够准确地预测海浪情况提出了EMD-LSTM模型，通过分析不同预报时间的预报效果，实证表明，EMD分解算法可以有效降低LSTM的误差且预报时间在相同的容忍度下可以提前一倍以上[11]。刘铭和单玉莹在预测股指时发现，在预测沪深300指数收盘价和深证成指收盘价时，EMD和LSTM组合模型有较好的预测效果[12]。

梳理前人的研究成果发现：长短期记忆网络在预测高频金融时间序列数据方面，相比传统模型准确性和精确度都更高，预测过程也比较简单；经验模态分解算法对数据自身的特征提取有着很好的表现。基于以上讨论，本文提出一种基于经验模态分解和长短期记忆神经网络的组合模型。

1 基本理论

1.1 经验模态分解

经验模态分解(empirical mode decomposition，EMD)是由Huang等于1998年提出的一种全新的自适应性强的时间序列数据分析算法[13]。EMD算法有3个假设条件：①原序列至少含有一个极大值和一个极小值；②特征时间尺度由极大值和极小值之间时间差决定；③若原序列无极值点，但有拐点，可通过求导求其极值。EMD分解对于任意时间序列y(t)计算流程如下：

步骤1找出原序列y(t)的所有的局部极大值和极小值，再用三次样条插值画出y(t)的上下包络线分别为m(t)和n(t),求其均值：

u(t)=(m(t)+n(t))/2

(1)

步骤2从y(t)中减去均值包络线u(t)，得到一个新序列d(t)，即

d(t)=y(t)-u(t)

(2)

步骤3判断新序列d(t)是否满足IMF的两个条件：①在整个时间尺度内，d(t)所有的局部极值点的个数和零点个数要么相等，要么最多相差一个；②在整个时间尺度范围任何时间点上，其上、下包络线均值恒为0。若满足，则d(t)是原始时间序列的一阶本征模函数，即d(t)=IMF1，若不满足，将d(t)看作是原始时间序列，重复步骤上述步骤，直到d(t)满足IMF的两个条件为止。

步骤4从原始时间序列y(t)中剔除IMF1，得到新的序列,重复以上步骤，得到IMF2、IMF3… 和一个残差项r(t)。则原始序列y(t)可表示为

(3)

1.2 样本熵

样本熵(sample entropy,SE)是Richman和Moornan在近似熵原理的基础上提出的一种改进的衡量时间序列数据自身波动复杂程度的度量方法[14]。时间序列自身前后的波动的重复性和周期性，即该时间序列数据前后自相似性的概率大小。若测得一个时间序列数据的样本熵值很大，那么意味着该序列中有很多的杂乱的信号，该时间序列数据本身在震荡前后的相似度就越低，就有很大概率产生新模式，因而序列本身就越复杂。对任意一个包含有n个数据的时间序列X={x1,x2,…,xn}样本熵的计算方法如下：

步骤1按序号构成(n-m+1)组m维向量空间时间序列，可表示为一个m(n-m+1)的矩阵。

步骤2计算任意两组向量Xm,i和Xm,j的距离d[Xm,i,Xm,j]。在任意两组向量一一对应的元素中，对应元素差值的绝对值最大的那一组对应元素的差值绝对值即为这两组向量的距离，即

d[Xm,i,Xm,j]=max|xi+k-xj+k|

(4)

式中：k=0,1,2,…,m-1；1≤i，j≤n-m+1。

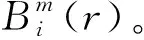
(5)

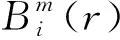
(6)

步骤5将原向量组的维数m提升到m+1，再对m+1维向量组进行重复上面步骤，得到Bm+1(r)。

步骤6该时间序列数据的样本熵值SE为

(7)

1.3 长短期记忆网络

长短期记忆网络(long short-term memory,LSTM)算法是一种改进的递归循环神经网络模型(RNN)。LSTM改进之处在于在原来的RNN结构中增加了“输入门”“遗忘门”“输出门”和隐藏单元控制门，能够及时有效地增加某些重要信息、剔除无关的信息以及处理时间或事件的影响。改进之后，LSTM模型有效地缓解了传统循环神经网络的梯度消失和梯度爆炸等问题。LSTM算法结构如图1所示。

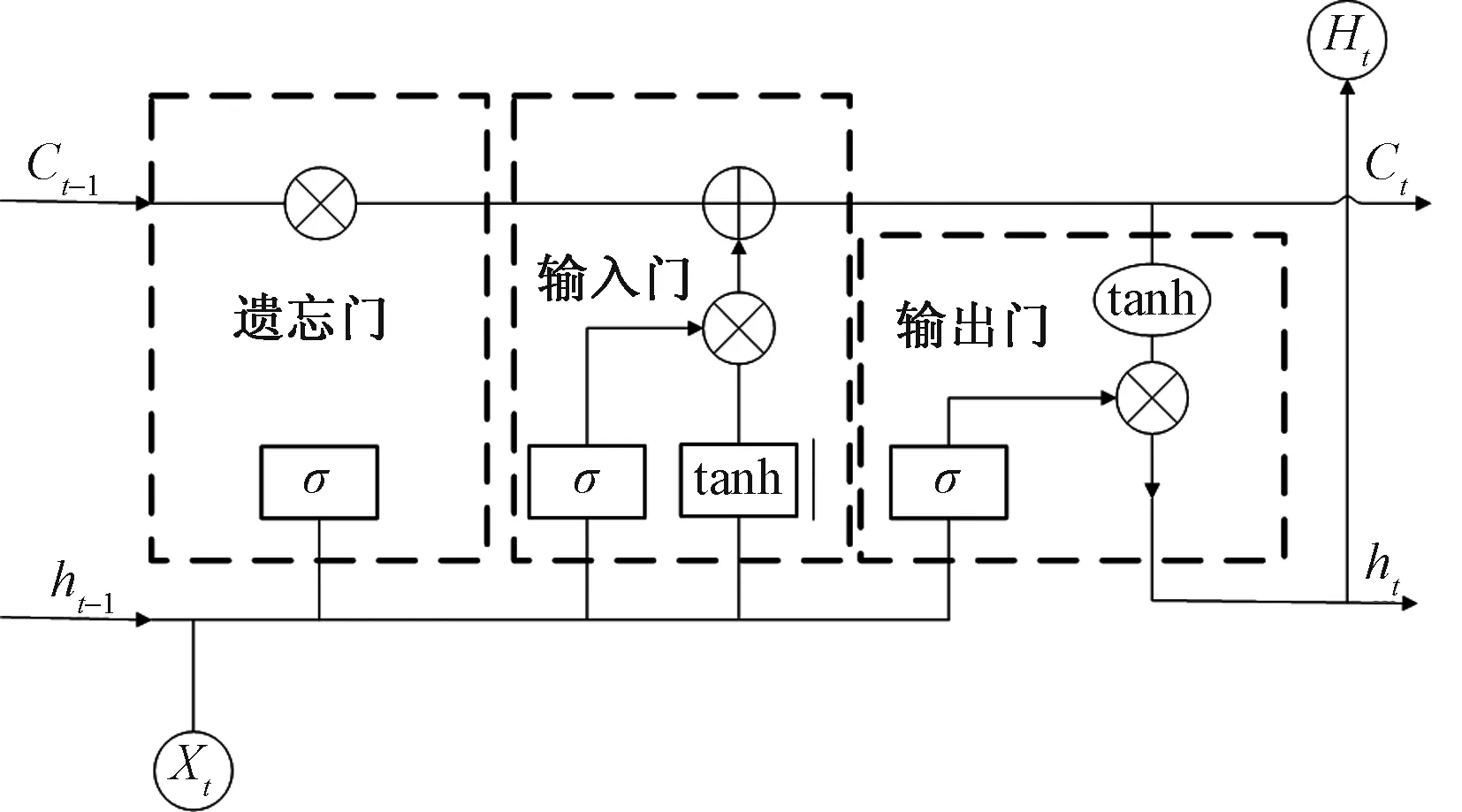
图1 LSTM算法结构

步骤1输入时间序列数据Xt和隐藏层单元状态ht-1经过“遗忘门”，得到此门细胞状态ft值，其计算公式为

ft=σ[Wf(ht-1,Xt)+bf]

(8)

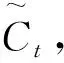
it=σ[Wi(ht-1,Xt)+bi]

(9)

(10)

步骤3输入时间序列数据Xt和隐藏单元层状态ht-1进入“输出门”，得到待输出结果ot和t时刻细胞状态Ct，待输出结果ot再经过细胞状态Ct的筛选得到最终的输出结果ht。

ot=σ[Wo(ht-1,Xt)+bo]

(11)

(12)

ht=ottanhCt

(13)

式中：σ为sigmod函数；Wf和bf为“遗忘门”的权值矩阵和偏置系数；Wi和bi分别为“输入门”的权值矩阵和偏置系数；Wc和bc分别为细胞状态更新后的权值矩阵和偏置系数；Wo和bo分别为“输出门”的权值矩阵和偏置系数；Ct-1表示t-1时刻的细胞状态。tanh为双曲正切激活函数，取值范围为[-1,1]。

1.4 EMD-SE-LSTM预测模型

结合各种算法的优势，构建EMD-SE-LSTM组合预测模型，从而更加精准预测股指波动率，其模型框架如图2所示。

图2 EMD-SE-LSTM预测模型框架

由图2可知，首先通过EMD算法将日内已实现波动率数据进行分解，得到不同频率、不同周期的本征模函数(IMF)序列和残差序列(Res)。再将这些IMF根据样本熵的大小分别重构成高频、中频和低频序列。最后通过LSTM算法进行滑动预测。将分解后的IMF序列和残差序列作为模型的输入数据集，经大量数据的训练，设定好模型的参数，得到一系列预测值，合并成最终的预测结果。

2 实证分析

2.1 数据处理与模型设定

以中证500指数为例，选取数据时间跨度为2019年1月2日到2021年5月24日每一分钟收盘

价，共有138 960个有效数据。为了避免隔夜效应对已实现波动率的影响，剔除了每日开盘第一分钟的收盘价。计算每分钟的对数收益率(即rt=lnPt-lnPt-1，其中Pt为第t时刻收盘价，Pt-1为第t-1时刻收盘价)，并采用1分钟和5分钟日内对数收益率平方和近似代替日内已实现波动率，最终形成579条有效样本数据。全部样本数据分为两部分，第一部分作为预测的训练集，取前522条数据；第二部分作为测试集，取后57条数据。全文以1分钟日内已实现波动率(图3)样本为例进行详细介绍。

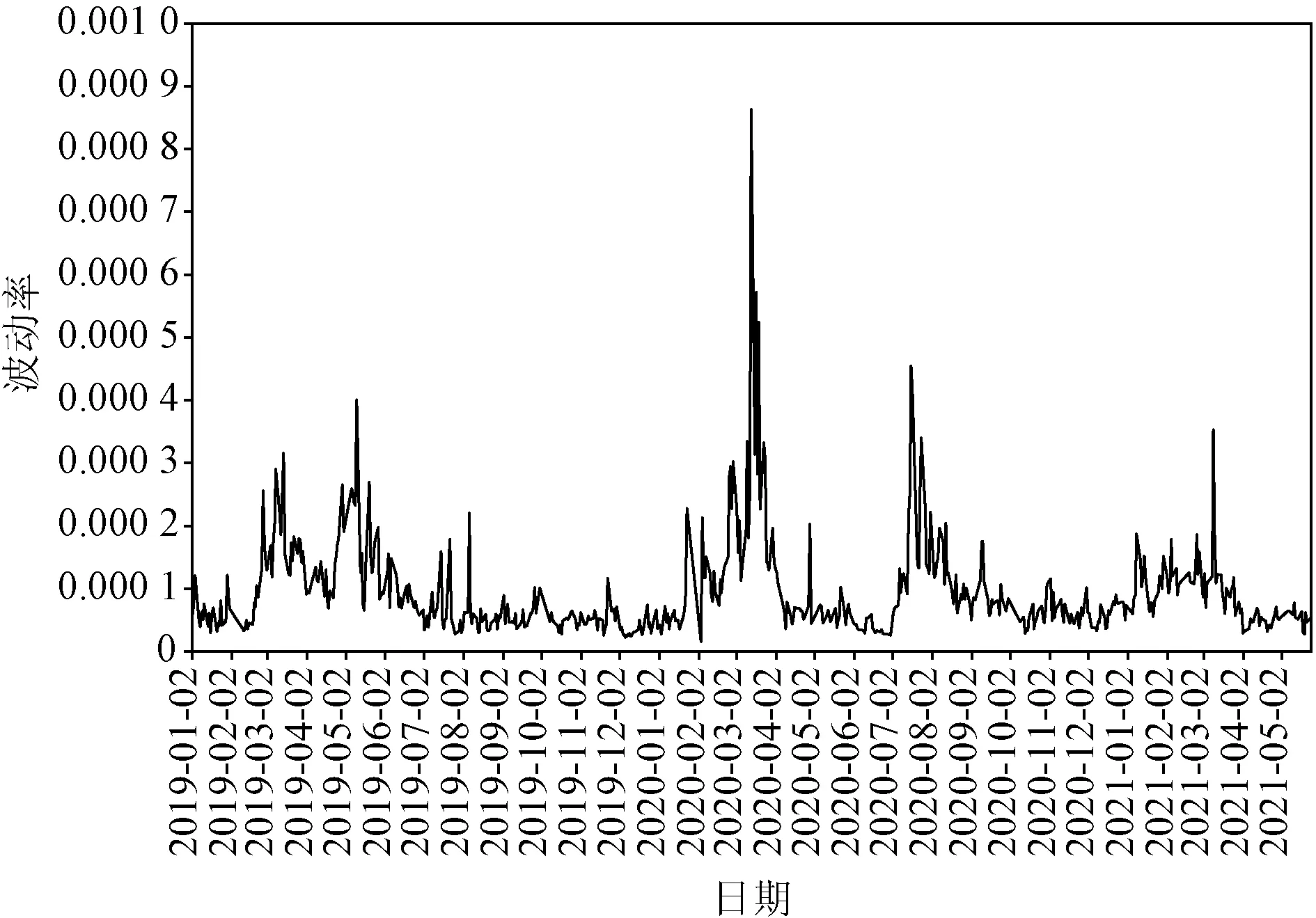
图3 1分钟日内已实现波动率

在EMD-SE-LSTM模型中，LSTM模型结构选择单层GPU，以均方根误差(RMAE)作为损失函数。LSTM层含有300个隐含单元,在指定训练项，将求解器设置为Adam算法并进行500轮训练。使用动态学习算法，初始学习效率为0.005，在进行125轮训练后，通过乘以因子0.2来逐渐衰减学习效率。设定ARMA模型时，先对原始时间序列进行了单位根检验，再进行数据平稳化处理。在构建ARMA(p,q)模型参数设置时，经过多次调试，根据信息准则AIC、SC和HQ最小原理，在进行1分钟和5分钟日内已实现波动率建模时，分别选择了ARMA(2,2)和ARMA(1,3)。

2.2 EMD分解

使用MATLAB软件实现EMD算法对数据正交分解，根据数据自身的时间尺度分解成不同频率的7个IMF序列和一个残差序列Res。各序列统计指标见表1,各序列走势如图4所示。

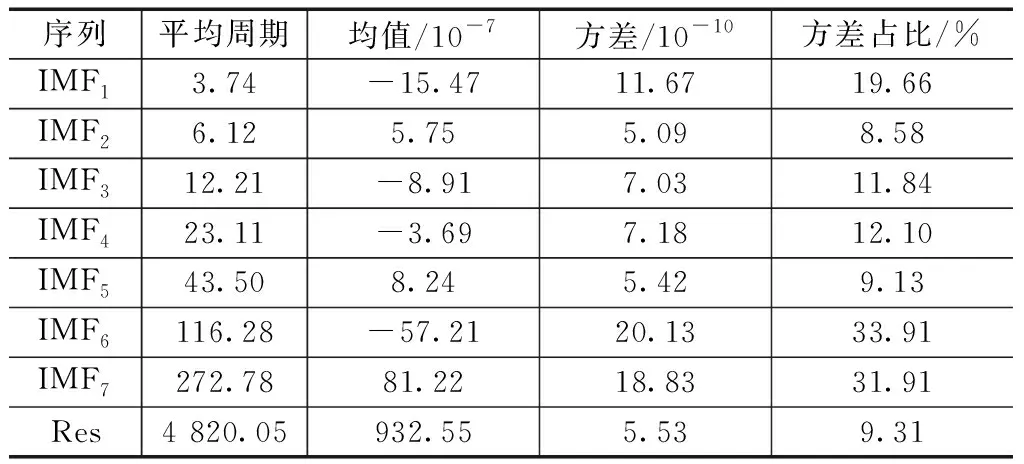
表1 各序列统计指标

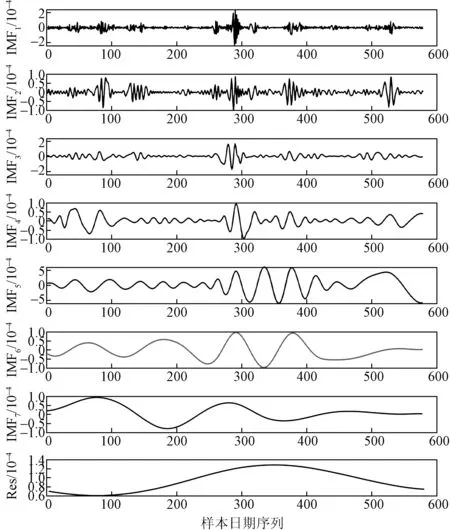
图4 EMD分解的IMF和残差序列Res

2.3 基于SE的IMF重构

本文研究的IMF分量较多，如果对于每个IMF分量都分别进行LSTM算法预测，由于在建模过程中每个IMF分量都会产生相应的误差，IMF分量越多所产生的误差就会越大，最后在合并预测结果的时候，所累积的误差就越大，最后在很大程度上影响了预测结果的精度。因此，本文提出了在将IMF分量进行LSTM建模前进行样本熵重构处理。计算出原始序列、IMF1～IMF7以及残差项Res的样本熵分别为0.218、2.309、1.432、0.731、0.517、0.328、0.062、0.048和0.027。其中IMF1～IMF5的样本熵都是大于原始序列的样本熵，IMF6和IMF7都是小于原始样本熵。因此本文将IMF1和IMF2合并成高频序列，IMF3～IMF5合并成中频序列，IMF6和IMF7合并成低频序列。

2.4 模型评价指标

为了客观量化地评价各个模型的拟合水平，本文选取了均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和纳什效率系数(R2)4个指标来评价模型的拟合优度。计算公式如下：

(14)

(15)

(16)

(17)

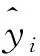
2.5 EMD-SE-LSTM预测结果

2.5.1 1分钟日内已实现波动率预测结果

通过比较ARMA(2,2)、LSTM和EMD-SE-LSTM模型的均方根误差、平均绝对误差、平均绝对百分比误差和纳什系数可知，EMD-SE-LSTM的4项统计指标均优于其他模型，可以说明EMD-SE-LSTM模型的预测准确性、预测精度和模型的拟合优度均是最好的。各模型预测统计指标见表2，结果走势如图5所示。

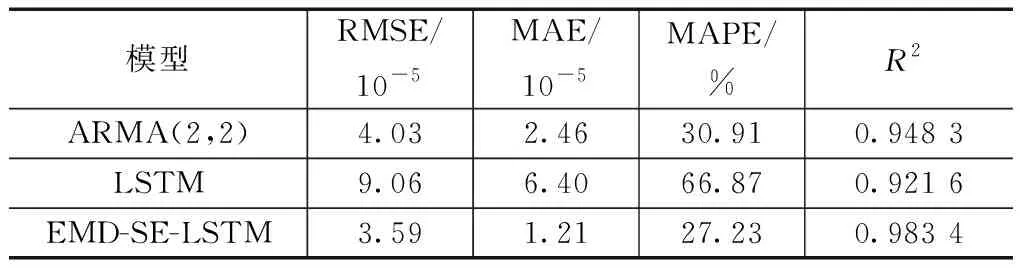
表2 各模型1分钟日内已实现波动率预测统计指标值

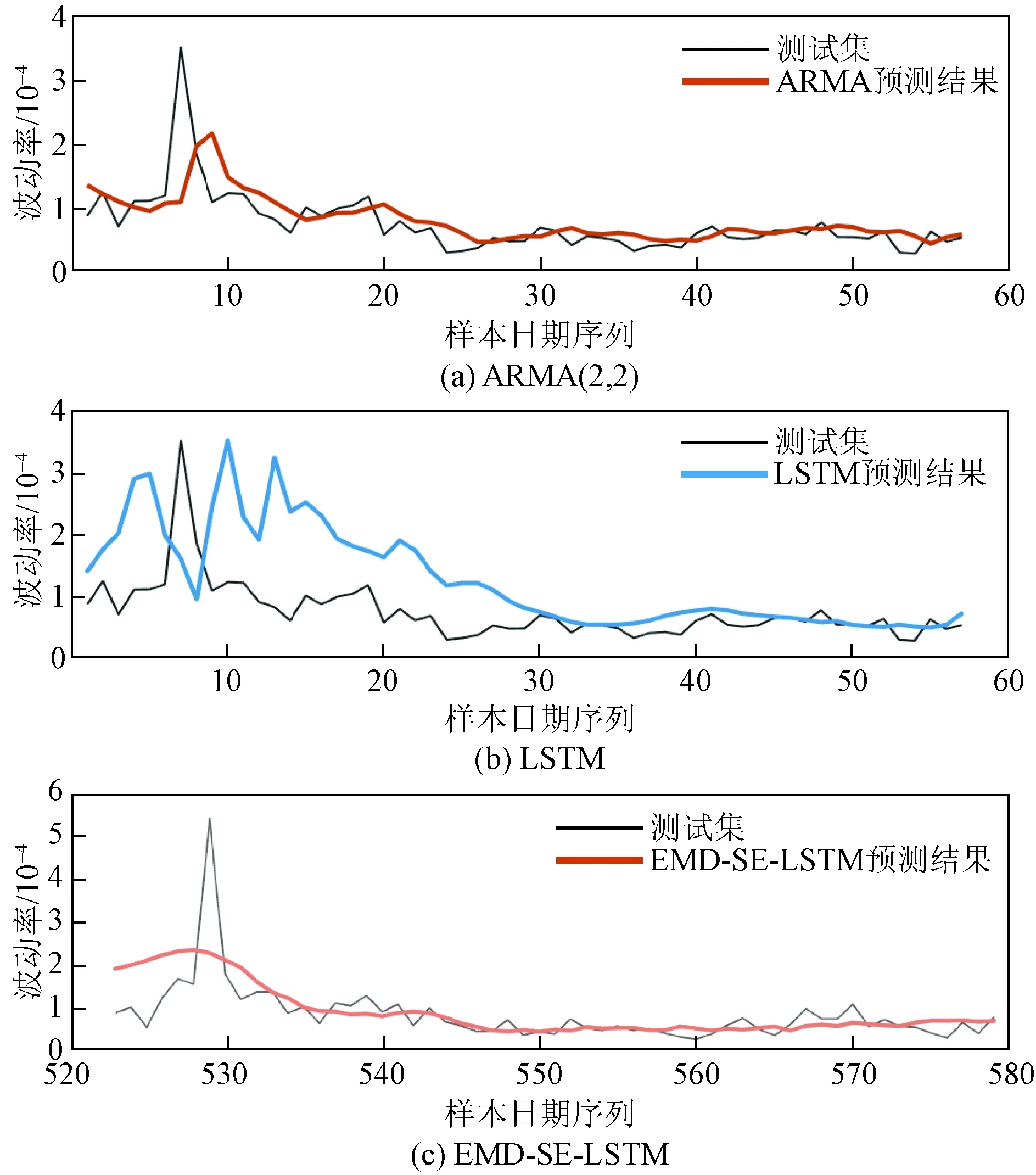
图5 各模型1分钟日内已实现波动率预测结果

通过EMD-SE-LSTM模型与单独的LSTM模型预测结果统计指标对比，使用EMD分解算法后的LSTM模型，精确度评估指标RMSE从9.06×10-5降低到3.59×10-5，均方根误差减少了5.47×10-5，MAE从6.40×10-5降低至1.21×10-5，平均绝对误差减少了4.19×10-5，MAPE从66.87%降低至27.23%，降低了39.64个百分点，而拟合优度从0.921 6提升至0.983 4。这足以表明本文引用的EMD分解算法能够有效地提取股票指数波动率的特征，提高了LSTM模型的预测精度和拟合优度。

从预测结果图5来看，EMD-SE-STM模型的预测效果明显比ARMA模型和LSTM模型好，ARMA模型预测效果次之，LSTM模型预测值与真实值有很明显的误差并且预测值的走势与真实值的延迟输出很类似，延迟的大小在两个工作日左右。通过对比EMD-SE-LSTM模型和单独的LSTM模型预测走势图，可以直观地知道EMD-SE-LSTM组合模型的预测值和真实值拟合得更好，预测值更贴合真实值的走势，误差更小，延迟效果也更小了。从而可知，EMD分解算法提高LSTM预测模型的效果。在面对股指波动率出现异常值方面，EMD-SE-LSTM模型很好地克服了波动率异常值的影响，使得预测结果更加平滑。

2.5.2 5分钟日内已实现波动率预测结果

5分钟日内已实现波动率实证过程与1分钟日内已实现波动率一致，故不再进行详细介绍，只给出最终结果，如表3和图6所示。

表3 各模型5分钟日内已实现波动率预测统计指标值

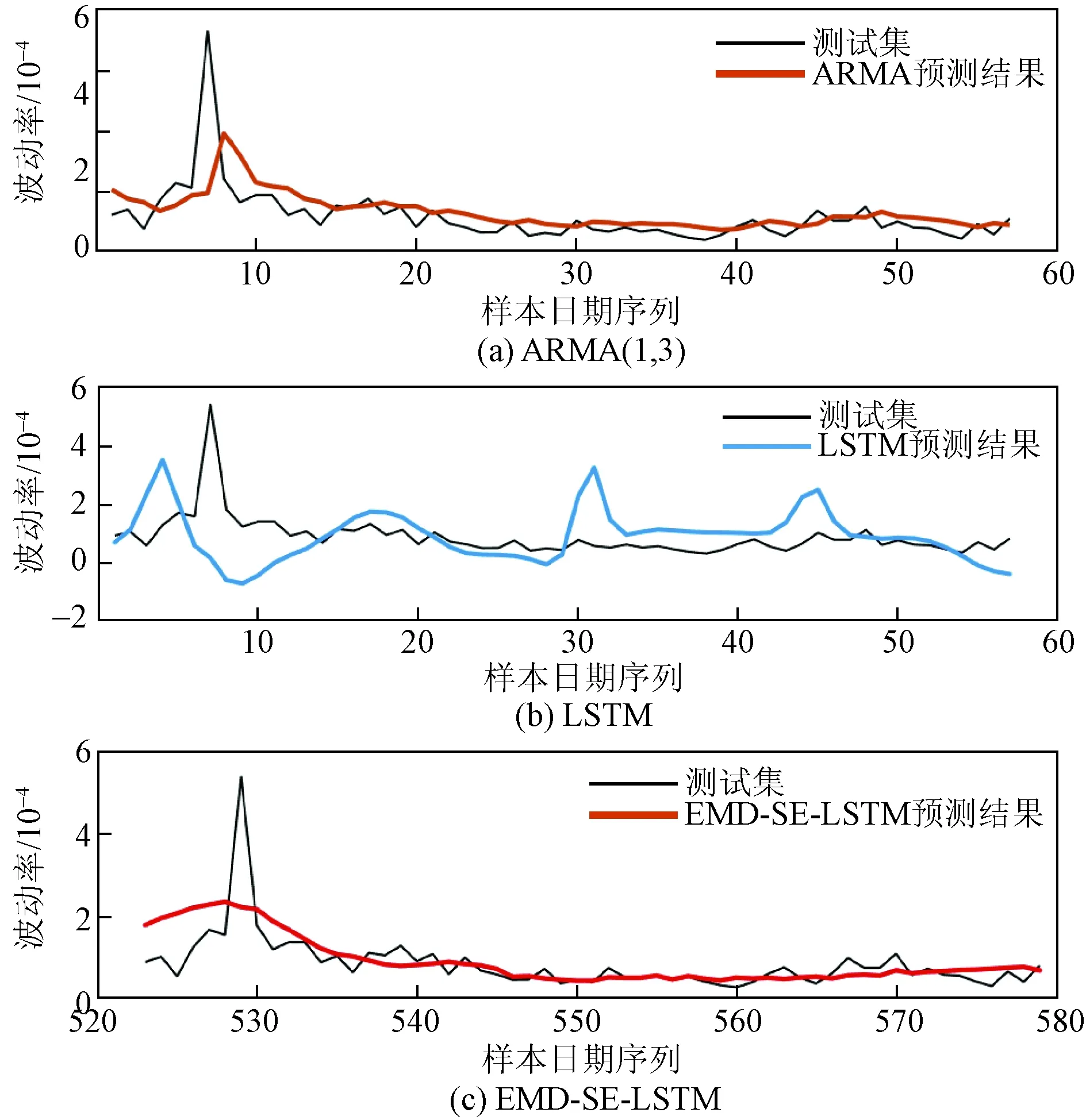
图6 各模型5分钟日内已实现波动率预测结果

由最终结果对比分析，可以得出EMD-SE-LSTM模型在衡量模型精确度和拟合优度的4个指标评估下同样表现最佳。总体而言，针对不同频率的已实现波动率，不管是从统计指标来看，还是预测结果走势图对比分析来看，EMD-SE-LSTM模型均能表现出最佳的预测效果。同样也可知，EMD分解算法对于LSTM模型预测效果有很大的提升。

3 结论

在股票市场中，由于股票指数波动具有高度嘈杂、非线性、动态、非平稳等特点，预测股指波动率的变动显得格外棘手。面对传统的预测模型预测的结果并不那么理想，因此本文提出了EMD-SE-LSTM组合模型对股指波动率进行预测。实证结果表明：EMD-LSTM组合预测模型在预测精确度和模型的拟合优度方面均超越其他模型，非常适合股票指数波动率的金融高频数据预测；此外，EMD算法通过有效提取股指波动率的特征，提升了LSTM模型的预测效果，同时也体现了EMD算法对动态、非平稳数据处理的良好效果。本文提出的EMD-SE-LSTM组合预测模型为研究金额高频时间序列数据预测提供了新思路，为进一步预测国内外股指波动率奠定了基础。