浮式风力机运动形式对尾迹大尺度运动的影响
李曌斌,董国丹,秦建华,周志登,杨晓雷,*
(1. 中国科学院 力学研究所,北京 100190;2. 中国科学院大学 工程科学学院,北京 100049)
0 引言
为实现“3060”的碳达峰、碳中和目标,风能将在我国能源体系中发挥重要的作用。在大型风电场中,多数风力机将不可避免地受到上游机组尾迹的干扰。尾迹具有风速低和湍流脉动高的特征,影响下游风力机的来流风况,降低其发电功率并增加其疲劳载荷。因此,准确的尾迹预报对风力机结构设计和风电场的排布优化具有重要价值。
风力机尾迹具有动态变化的特点。尾迹最显著的动态特征是低频、大尺度的横向摆动[1-2],被称作蜿蜒(meandering)。从时均角度来看,蜿蜒将尾迹的速度亏损分散到一个更大的区域,增强了尾迹与周围空气的动量混合,加速了尾迹速度亏损恢复,最终提高了下游风力机的时均来流风速[3]。另一方面,尾迹蜿蜒使下游机组不断地在全尾迹、半尾迹和自由流之间切换,增大了其所受的非定常载荷[4]。关于尾迹蜿蜒的产生机制,通常认为有两种,分别是来流大尺度涡机制和剪切层失稳机制[1]。大尺度涡机制认为尾迹蜿蜒源自大气湍流的大尺度涡对尾迹的输运(通常需假定大尺度涡的特征长度大于2倍风轮直径[4])。这时尾迹像被动标量一样跟随来流大尺度涡运动(类似于烟线)。与之相对,剪切层失稳机制认为尾迹蜿蜒来自于尾迹本身的失稳,即尾迹促进了上游扰动的增长,并最终引起尾迹大尺度的横向摆动[5-7]。此外,最近的研究工作在对2.5 MW陆上风力机的尾迹蜿蜒进行数值模拟[8]和实地测量[9]研究后,发现两种机制在尾迹蜿蜒中同时存在。
值得注意的是,以上关于尾迹蜿蜒的理论多来自对陆上的固定式风力机的研究。对于漂浮式风力机而言,海上复杂的风、浪、流组合载荷将引起浮式平台和风力机的刚体运动,但该运动对尾迹演化的影响尚不清楚。这一问题在最近十年间引起了流体力学、风能和海洋工程领域学者的广泛关注。2012年,美国马萨诸塞大学Sebastian及Lackner使用自由涡方法研究了浮式风力机在俯仰运动下的叶轮载荷,报道了由风力机运动引起的近尾迹涡系失稳现象[10]。此后,韩国学者Tran和Kim用URANS(Unsteady Reynolds Averaged Navier-Stokes)方法开展了叶片解析的数值模拟,分析了俯仰和纵荡运动对叶片载荷的影响,同样发现了风力机运动对近尾迹涡系结构的破坏[11]。2014年,挪威科技大学De Vaal等在基于致动盘方法的尾迹模拟中发现风力机纵荡运动会引发远尾迹的收张式波动[12]。中南大学Chen等(2022)使用叶片解析的IDDES(Improved Delayed Detached Eddy Simulation)方法也发现了纵荡运动引起的远尾迹的收张式波动,并且发现该波动能加速尾迹恢复[13]。韩国科学技术院Lee等(2019)使用涡格/涡粒法对尾迹进行了数值模拟,发现简谐风力机运动会诱发远尾迹周期性的形变[14]。佛罗里达州立大学Kopperstad等(2020)在不规则波浪的激励下,同样发现了浮式风力机尾迹的大尺度低频波动[15]。值得注意的是,以上工作仅关注了与风向一致的运动形式,而最近的水动力分析发现,在风浪异向条件下浮式风力机将发生明显的侧向运动[16]。
近期工作中,本文作者团队发现了浮式风力机侧向运动能够诱发尾迹的蜿蜒,并基于线性稳定性理论发展了浮式风力机尾迹稳定性的评估模型,准确地预测了可以诱发尾迹蜿蜒的风力机侧向运动频段[17]。该工作说明平台运动是引起风力机尾迹蜿蜒的重要因素,剪切层失稳机制在浮式风力机尾迹蜿蜒中起到了重要作用。因而,有望以稳定性理论为框架预测浮式风力机尾迹的演化。
本文在文献[17]的基础上,拓展了浮式风力机的运动形式,考虑了纵荡、横荡、艏摇三个不同的自由度,以研究不同运动形式对尾迹影响的异同。
1 研究方法
1.1 尾迹的稳定性分析
首先介绍用于分析尾迹对不同频率扰动的增长率的线性稳定性理论。
分析中使用的基本流来自于固定风力机的时均尾迹,并作了局部平行和轴对称两个假设。基本流的流向、径向和周向的速度分别设为。设扰动速度和压强为其中 •ˆ表 示径向形状函数,n为扰动模态的周向波数。n=0表 示轴对称的扰动,对应纵荡情况;n=1表示反轴对称情况,近似对应横荡和艏摇下引起的扰动。
对扰动的空间增长进行分析。假设风力机整体的刚体运动的角频率 ω=2πf为实数。对每一个扰动频率 ω,求解与之对应的复波数k=kr+iki。若k的虚部ki<0,表明该扰动将在向下游发展的过程中增大,是不稳定的;反之,若k的虚部ki>0则表示扰动将在向下游发展的过程中减小,是稳定的。
将扰动表达代入线化的Navier-Stokes方程,可得:

注意,上述方程忽略了黏性项。这一假设在基本流剖面存在拐点时是合理的,这时尾迹失稳由无黏的K-H不稳定性主导。
方程通过Chebyshev多项式进行离散。径向计算域的大小设为rmax=15D,共使用了128个Gauss-Lobatto节点。在远场边界上假设扰动衰减为零。其他 边界条件参照文献[18]设置。
1.2 大涡模拟方法
本文采用大涡模拟和风力机的致动面模型来模拟不同形式的风力机运动对风力机尾迹的影响,使用的计算流体力学程序为VFS-Wind[19]。VFS-Wind 预测风力机尾迹的能力已经过风洞实验和实地观测的系统验证[20-21],并已应用于风力机尾迹的机理研究[22]。
流动的控制方程为滤波的不可压N-S方程:

其中:xi和ui代表直角坐标系下三个方向的坐标和速度分量(i,j= 1,2,3);p为 压强;ρ 为流体密度;υ为运动黏度;为空间滤波算符; τij为由滤波产生的亚格子应力,使用动态Smargorinsky模型进行封闭;fi表示单位质量流体所受的体积力,代表叶片、机舱等部件对流动的作用。
控制方程通过二阶中心差分进行空间离散,时间推进采用二阶分步方法。离散后的动量方程通过Jacobian-Free Newton-Krylov方法求解。压力泊松方程通过GMRES算法求解,并利用代数多重网格法进行加速。
1.3 风力机的致动面模型
本文使用致动面方法对风力机叶轮和机舱进行模化[23]。叶片的致动面模型使用无厚度曲面简化表达风力机叶片形状。各径向位置处的气动力通过从二维翼型数据库中查询升/阻力系数并按下式计算:
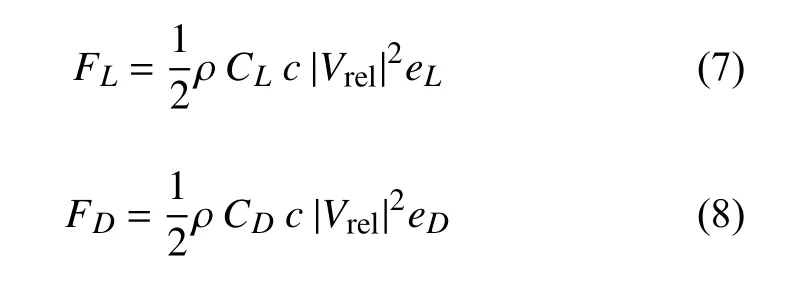
其中:FL和FD分别为单位长度翼型上的升阻力;c为翼型弦长;Vrel为叶片与来流的相对速度,在计算时考虑了叶片的转速以及浮式风力机刚体运动的影响;eL和eD分别为升、阻力的方向矢量;CL和CD为查表获得的升、阻力系数,对应当前的攻角和雷诺数。单位叶片面积上所受的气动力F通过下式计算,

并通过磨光基函数[24]散布到叶片周围的流体网格上。
1.4 研究对象和算例设置
以美国可再生能源实验室(NREL)5 MW 海上风力机标模为研究对象。叶轮直径D= 126 m。依正常发电的设计工况把来流风速设置为U∞= 11.4 m/s,叶尖速比固定为 λ=ΩR/U∞= 7(其中 Ω为叶轮角速度、R为风轮半径)。由叶轮直径和来流速度定义的雷诺数 为Re≈ 9.6 × 107。机 舱 用 长 方 体 近 似(2.3 m ×2.3 m × 14.2 m)。文献[17]中证明了塔柱的影响不大,因此在本工作中未予考虑。
研究了三种典型的风力机运动自由度,包括:纵荡、横荡和艏摇(见图1)。这三种自由度对应xOy平面内的平动和转动,最易引起尾迹蜿蜒(发生在轮毂高度平面上)。在各自由度下,风力机均做强制的简谐运动。运动控制参数为频率f和幅值A。其中,纵荡、横荡的幅值为A=0.05D。艏摇角度的幅值满足sin(γmax) =A/R =0.1。因此,三种运动形式具有相同的叶尖运动幅值。风力机运动的频率f用无量纲的Strouhal数来表示,定义为St=fD/U∞。在各运动自由度下,均选取St= 0.1,0.3,1.0三个典型频率,分别代表低、中、高频率的扰动。以OC3 Hywind Spar单柱式浮式基础为例,以上频率分别近似对应系统(包含风力机和系泊装置)的纵荡、横摇、艏摇的固有频率[25-26]。大涡模拟中未考虑各自由度的组合。表1总结了本文考虑的风力机运动的形式及控制参数。

表1 浮式风力机强制运动参数Table 1 Parameters of wind turbine motions
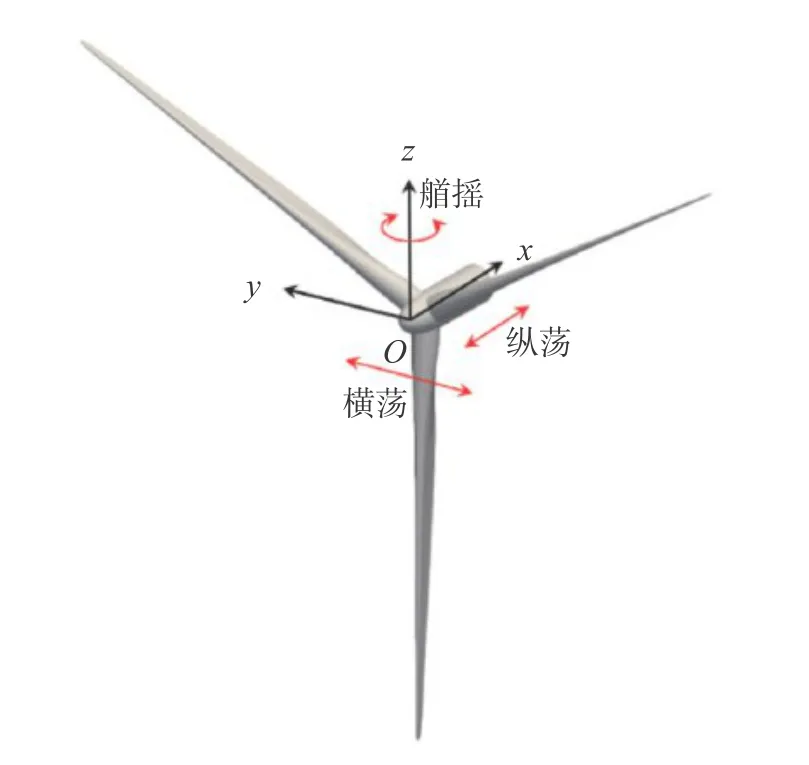
图1 本文选取的三个浮式风力机运动自由度Fig. 1 Sketch of platform motions
大涡模拟的计算域为长方体,在流向(x)、横向(y)和垂向(z)三个方向的长度分别为Lx,Ly,Lz=14D,7D,7D。风力机距入口边界3.5D。坐标系原点与风力机轮毂中心重合。入口边界施加均匀来流的速度条件。出口边界(x= 10.5D)施加速度导数的诺伊曼条件( ∂ui/∂x= 0)。侧向四个边界上均施加滑移条件。计算域用笛卡尔网格进行离散。流向网格大小为Δx= Δz/20。在y和x方向上,在尾迹区域内(y×z∈[−1.5D,1.5D] × [−1.5D,1.5D]),网 格 间 距 为Δy= Δz=D/40,在此区域外网格的尺寸逐渐增长。网格总数为Nx×Ny×Nz= 281 × 141 × 141 ≈ 5.6×106。根据之前的网格无关性验证,该网格分辨率满足预测尾迹速度和湍流强度的要求[3]。
2 稳定性分析结果
图2给出了尾迹的线性稳定性分析结果。分析使用的基本流是固定式风力机的时均尾迹,通过大涡模拟方法获得。图2(a)展示了机舱轮毂平面上时均流向速度亏损分布。由图可见,在x< 1D范围内可以观察到y= 0附近的机舱尾迹。尾迹核心区域和自由流之间存在剪切层,剪切层厚度在下游逐渐增加。在x> 7D之后的区域,尾迹两侧的剪切层在中心汇合,这时尾迹的速度亏损廓线(红色曲线)与钝体尾迹的高斯剖面相似。
图2(b)、图2(c)分别给出了扰动的周向波数取n= 0和n= 1两种情况下,各流向位置的扰动局部增长率。从图中可以看出,近尾迹(x <3D)的失稳频率范围很广,只要扰动的无量纲频率在 0 <St< 0.9范围内,几乎都是不稳定的,这与近尾迹较窄的剪切层厚度有关。用红色虚线标出的最不稳定的扰动频率约对应St≈0.5。两种波数下(n= 0,n= 1),失稳频段均沿流向逐渐降低。在x= 9D处,轴对称扰动(n= 0)的最不稳定频率几乎降至St= 0(如图2(b));非轴对称扰动(n= 1)的最敏感频率则降至约St= 0.1(如图2(c))。这与尾迹剪切层的厚度增加有关[6]。这种失稳频段沿流向的变化,说明不同下游位置处的最优扰动频率各异。因此,高频扰动虽然在近尾迹中增长较快,但在下游很快就停止增长。与之相反,频率较低的扰动虽然在近尾迹增长较慢,但可以持续保持增长。周向波数(n)的影响主要体现在远尾迹。从图2(b)中可以看出,轴对称扰动(n= 0)只在x< 6D范围内有较明显的增长;而图2(c)中非轴对称的扰动(n =1)的增长则可保持到约x= 8D。

图2 基于固定式风力机时均尾迹的线性稳定性分析结果Fig. 2 Linear stability analyses based on the time-averaged wake of a fixed wind turbine
为了考虑扰动从风力机所在位置起(x= 0)一直发展到下游的过程,用局部增长率( −ki)沿流向x的积分构造扰动的累积放大系数累积放大系数近似地代表了扰动在流向上的累积增长。图2(d)、图2(e)比较了不同频率的初始扰动在各流向位置处x的累积放大系数。对于两种周向波数,累积放大系数均在向下游发展的过程中逐渐增长,且均在7D<x< 10D范围内达到最大。在远尾迹,周向波数n对累积放大系数有较大的影响。轴对称扰动(n =0)的累积放大系数最大值约为Nmax≈13,非轴对称扰动(n =1)的累积放大系数最大值可达Nmax≈18,说明非轴对称扰动更容易在远尾迹产生剧烈的波动。图2(d,e)中用红色虚线绘出了不同位置处的累积放大系数对应的峰值频率,该频率随着流向距离x的增长而降低。在7D<x< 10D的远尾迹,轴对称扰动(n= 0)对应的最优扰动频率约在0.3 ≤St≤ 0.5区间,非轴对称扰动(n= 1)对应的最优扰动频率约在0.2 ≤St≤ 0.4区间。在St≤ 0.1的低频段以及St≥ 1.0的高频段,两种周向波数的累积扰动放大系数均不高,说明这些扰动在尾迹中增长较慢。
以上的线性稳定性分析可以快速地给出尾迹的不稳定特性。但要注意,以上分析依赖于如下假设,即:(1)基本流是平行且轴对称的;(2)扰动是无限小的;(3)忽略黏性效应。这些假设不能完全代表实际情况,例如:实际的基本流通常更加复杂且基本流会因扰动而改变;扰动是有限幅值的,扰动幅值较高后会引发非线性效应;黏性效应将减弱扰动的增长,降低扰动放大率。因此,下一节将利用高可信度的大涡模拟方法对本节的分析进行检验。
3 大涡模拟结果
图3中比较了固定和三种运动形式下的风力机尾迹。风力机运动的无量纲频率为St= 0.3。图中用瞬时速度的等值面绘出了瞬时尾迹的三维结构,其中绿色为U=0.8U∞的 等值面,蓝色为U=0.5U∞的等值面。从图3(a)中可见,固定式风力机的尾迹几乎呈平直状向下游发展,未有明显的大尺度波动。但在风力机发生运动时,尾迹均发生了较为明显的大尺度波动。从图3(b)中可见,纵荡运动使U=0.8U∞的等值面发生了有节律的收张,扩张段内部可见明显的U<0.5U∞的低速区,说明了风力机纵荡增大了尾迹的流向速度的脉动强度,与文献[12-13]相符。这时风力机尾迹的中心线仍基本保持平直,轮廓大致保持轴对称的形状。图3(c)给出了横荡状态下的尾迹速度轮廓,展示了尾迹在xOy平面内的明显蜿蜒现象,尾迹蜿蜒的幅值在下游逐渐增大,在远尾迹与风力机叶轮直径相当。这种尾迹蜿蜒的现象同样发生在风力机艏摇运动下(图3d),但艏摇运动引起的尾迹蜿蜒幅值小于横荡运动。另外,尾迹中未见大范围的低速U<0.5U∞区域,表明横荡、艏摇对尾迹的主要影响并非是流向速度的波动,而是横向的蜿蜒。
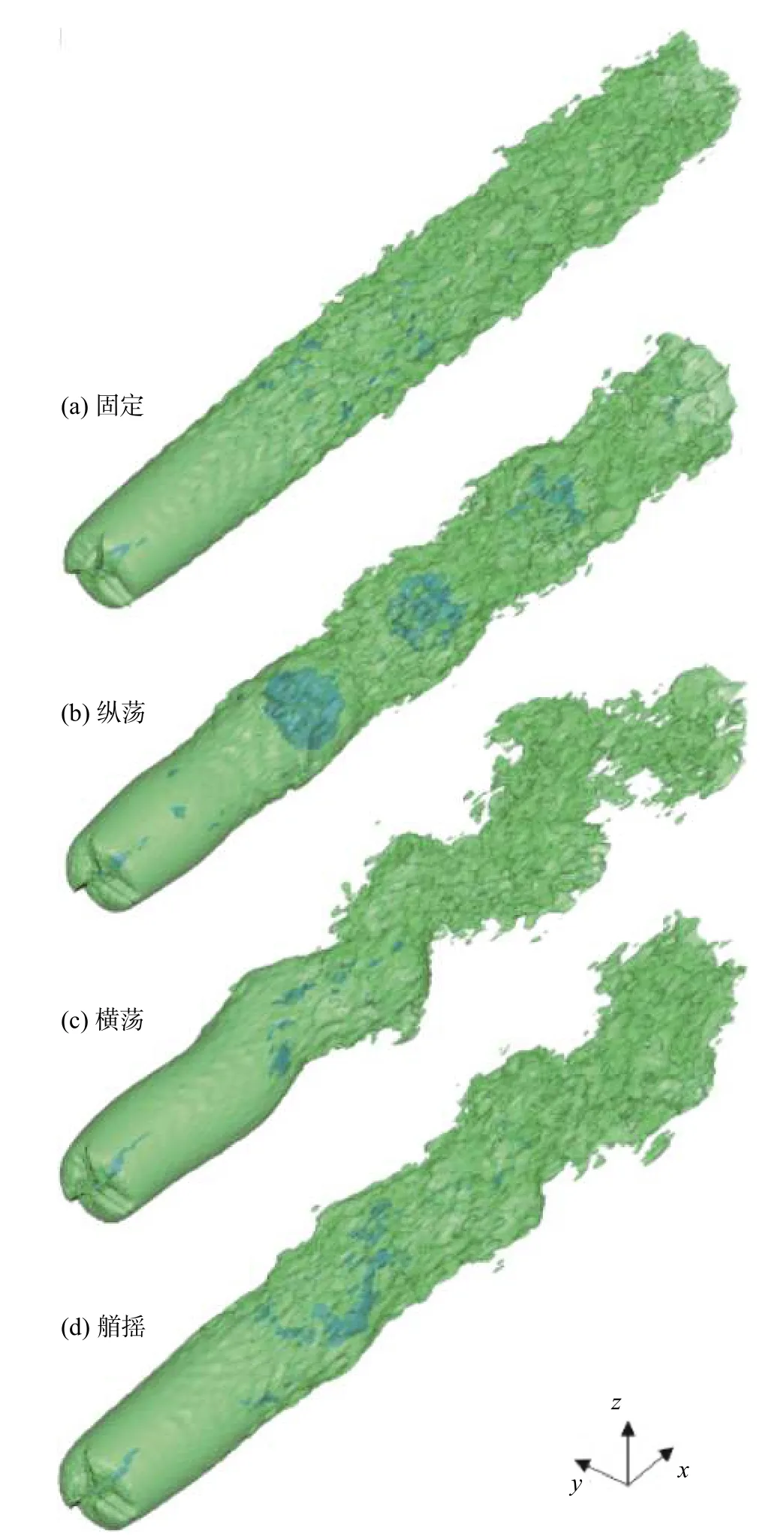
图3 不同运动形式下风力机力尾迹速度的等值面(运动无量纲频率为St = 0.3)Fig. 3 Isosurfaces of the wake velocity for different turbine motions (St = 0.3)
从图3中可知,三种运动均未引起尾迹的垂向起伏。因此,后文将在轮毂高度的水平面内开展分析。
图4给出了轮毂高度平面上风力机纵荡下尾迹的瞬时速度亏损云图,对St= 0.1,0.3,1.0三个运动频率的影响进行了比较。从图4中可见,尾迹中心线均基本沿y= 0保持平直,但不同运动频率下,尾迹的波动状态区别较大。三种运动频率下的尾迹基本沿y= 0保持对称,支持了稳定性分析中使用的轴对称扰动假设(n =0)。在不同的风力机运动频率下,尾迹的演化特征具有较大差异:(1)当风力机运动频率为St= 0.1时,其尾迹与固定式风力机的尾迹非常接近—尾迹边缘在x< 3D段保持平直,并在远尾迹产生了小尺度的速度波动。(2)当风力机运动频率为St= 0.3时,近尾迹(x< 3D)仍与固定式风力机尾迹相差不多,但远尾迹出现了明显的、大尺度的交替收张:在尾迹舒张段,尾迹核心区域内可见与尾迹宽度相当的低速流动结构;尾迹的收缩段的流速则相对较快;二者交替出现,增加了流向速度脉动的强度。(3)当风力机运动频率为St= 1.0时,风力机运动在近尾迹即引起了尾迹边缘的小尺度波动,但这种波动没有在下游持续地增长,最终未能形成贯穿尾迹核心区域的大尺度结构。这时尾迹总体轮廓与固定式风力机的尾迹相似。综上,在三个频率当中,St= 0.3的风力机运动对尾迹波动的贡献最显著,与线性稳定性分析的结果相符合(如图2(d))。
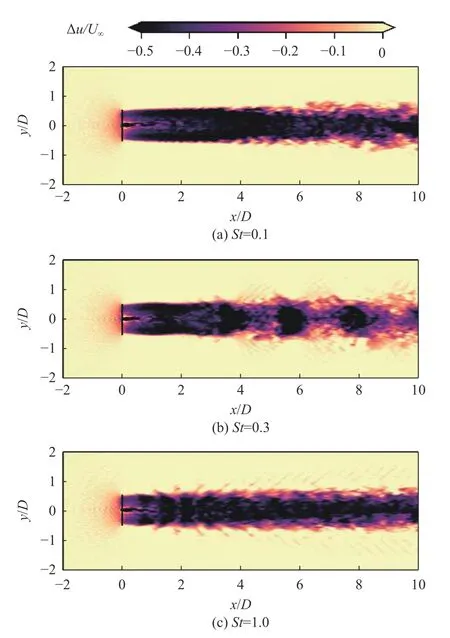
图4 纵荡运动下的尾迹瞬时尾迹速度亏损云图Fig. 4 Instantaneous wake velocity fields for cases with surge motion
图5 给出了在轮毂高度平面上风力机横荡运动下的尾迹瞬时速度场。图5也表明St= 0.3的风力机运动将引起较明显的尾迹蜿蜒,而St= 0.1和St= 1.0两种情况下尾迹的波动较小。当风力机在St= 0.1频率下做简谐运动时,尾迹的摆动幅值较小,轮廓总体与固定式风力机的尾迹相似。在频率为St= 0.3的情况下,风力机运动使尾迹出现了明显的蜿蜒,且蜿蜒幅值持续增长,最后可超过风轮直径。在这种剧烈的蜿蜒下,尾迹核心区域的速度亏损恢复加快,且势必显著增强尾迹的速度脉动。St= 1.0的高频风力机运动同样没有引起尾迹的整体蜿蜒,仅在尾迹边缘处出现了小尺度的波动。随着向下游的发展,这些波动的幅值并无明显增长。这些现象同样与线性稳定性理论的结果(如图2(e))相符,即在0.2 ≤St≤ 0.4区间内的扰动较易引起尾迹的失稳,而在St≤ 0.1的低频段以及St≥ 1.0的高频段的风力机运动较难对尾迹产生明显影响。
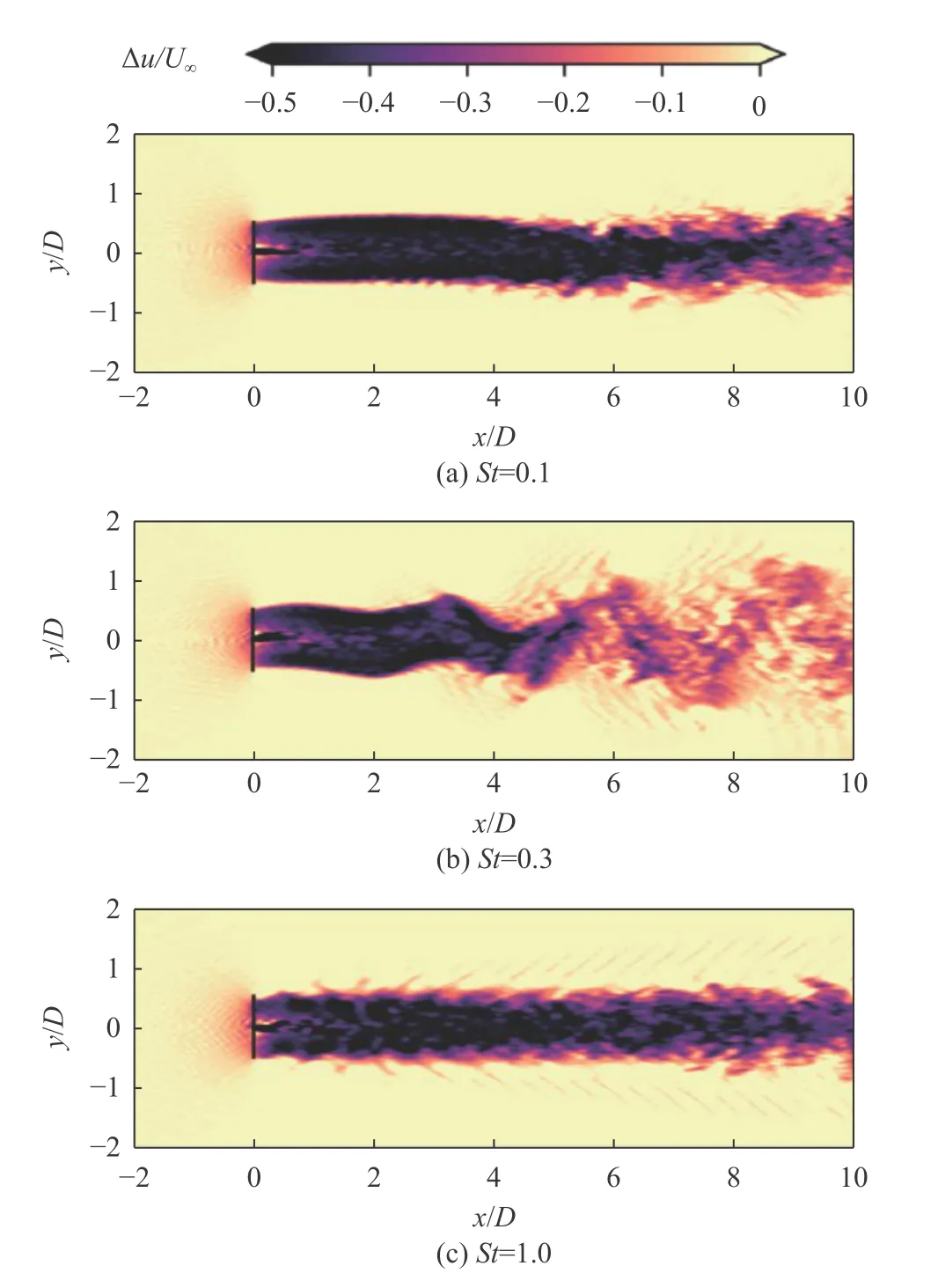
图5 横荡运动下的尾迹瞬时尾迹速度亏损云图Fig. 5 Instantaneous wake velocity fields for cases with Sway motion
图6 给出了风力机艏摇运动下的尾迹瞬时流向速度场。在艏摇状态下,风力机尾迹时空演化特征与横荡状态(图5)非常相似,在St= 0.3的频率下出现了较为明显的尾迹蜿蜒,而频率为St= 0.1和St= 1.0的风力机艏摇运动未能引起明显的尾迹波动。
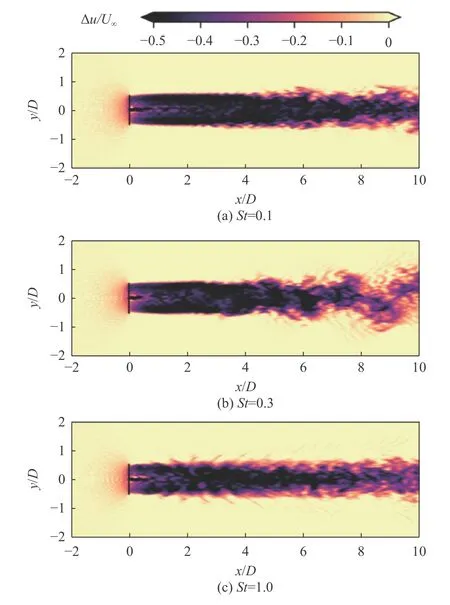
图6 艏摇运动下的尾迹瞬时尾迹速度亏损云图Fig. 6 Instantaneous wake velocity fields for cases with yaw motion
以上结果表明三种扰动均在St= 0.3的频率下引发了较为明显的尾迹波动,而St= 0.1及St= 1.0的运动频率均不易引发尾迹波动。这一规律均与线性稳定性理论的预测相符,说明三种形式的运动对尾迹影响的机制均为剪切层失稳,线性稳定性分析可以作为估计敏感频率的快速计算工具。但是,三种运动方式引发的尾迹演化特征存在差异。纵荡运动对尾迹的影响主要表现为尾迹轮廓的舒张和流向速度的交替波动,尾迹中心线几乎不发生摆动。与之相反,横荡、艏摇对尾迹影响的主要表现为横向的蜿蜒,具有相似的机理。但是,二者引起的尾迹蜿蜒剧烈程度明显不同—在艏摇运动下,尾迹蜿蜒的起始位置距风力机更远,且蜿蜒的幅值更低。虽然本工作在运动幅值的设置上保证了两种运动具有相同的叶尖最大位移,但这种位移相等的条件未能保证二者在尾迹动力学上的等价。
图7比较了不同风力机运动条件下尾迹的时均速度亏损。由图可见,在x =6D位置处,无量纲频率为St= 0.3的横荡运动比其他运动形式更能促进时均尾迹的恢复。在x =9D位置,St= 0.3的横荡、艏摇运动均使尾迹恢复速度显著加快,且横荡运动的作用更明显。以上现象说明合适的风力机运动具有促进尾迹恢复、增加下游风力机发电输出的潜力。
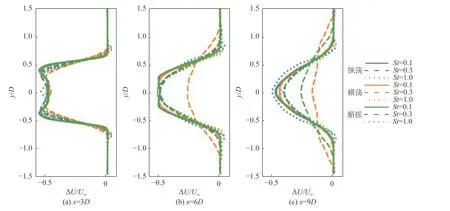
图7 风力机运动对尾迹时均速度亏损廓线的影响比较Fig. 7 Comparisons of velocity deficits of wind turbines subjected to different motions
4 结论与展望
本文研究了浮式风力机尾迹在纵荡、横荡、艏摇三种运动形式下的演化规律。利用线性稳定性理论,预测了尾迹在轴对称和非轴对称两种理想扰动下的敏感频率。然后,利用大涡模拟研究了不同形式、不同频率的浮式风力机刚体运动对尾迹产生的影响,检验了线性稳定性理论预报浮式风力机尾迹失稳演化的能力,并比较了不同运动形式、频率下的尾迹动态特征。最后,从风力机尾迹演化的角度讨论了浮式风力机设计中应重点考虑的刚体运动形式和频率范围。研究得出以下结论:
1)风力机运动的不同形式将使尾迹产生两种不同于固定式风力机尾迹的演化模式。第一种为收张模式,在风力机纵荡运动下产生,表现为远尾迹轮廓有节律地收缩和舒张,并伴随高、低速交替的流动结构。第二种为尾迹蜿蜒,在风力机横荡、艏摇两种运动下产生,表现为尾迹的横向甩动。
2)在不同的运动形式下,能够引起尾迹显著动态响应的频段相近。线性稳定性分析结果显示,轴对称扰动(纵荡)的失稳敏感频率范围约为0.3 ≤St≤ 0.5;非轴对称扰动(横荡和艏摇)的失稳敏感频段范围约为0.2 ≤St≤ 0.4。大涡模拟结果表明,当St= 0.3时,三种运动形式均在远尾迹产生了较为剧烈的波动;而St= 0.1和St= 1.0的低频和高频情况下,尾迹均与固定式风力机尾迹较为相似。
3)剧烈的尾迹蜿蜒一方面将引起下游风力机载荷的振荡,另一方面又能促进尾迹恢复,提升下游机组功率。因此,在浮式风力机的设计中,应慎重评估无量纲频率在St= 0.3附近的风力机运动的潜在影响。
下一步的工作展望:
1)横荡、艏摇两种运动形式对尾迹蜿蜒的影响机理的差异仍待进一步研究。本工作中在设定运动幅值时,设置了相等的叶尖最大位移,但两种运动引起的尾迹蜿蜒存在差异。因此,两种运动形式之间的关联与差异性有待开展深入研究。
2)本文仅考虑了三个典型自由度下简谐运动的影响。在线性稳定性的理论框架下,扰动演化满足线性叠加原理,因此本文的理论分析可以应用到非规则运动及多自由度运动的情况下。但实际情况下,有限幅值的扰动将引起非线性效应,因而浮式风力机在复杂运动下的尾迹演化仍需使用高可信度仿真进行考察,有待在下一步工作中深入研究。
3)本文仅考虑了一种风轮转速。改变风轮转速将改变风力机工况,进而改变风力机尾迹的速度亏损特征。文献中的研究结果表明[8],在一定的风轮转速范围内,固定式风力机的尾迹蜿蜒的特征相近。对于改变风轮转速将如何影响浮式风力机运动引发的尾迹蜿蜒,仍有待进一步研究。
4)下一步工作中还可以考虑平台尾迹[27]、水波[28]与尾迹间的相互作用。

