例析“角平分线”在思路探究中的作用

⦿甘肃省武威市天祝藏族自治县新华中学 赵 霞

1 引言

经历了几何解题思路探究的过程后，人们通常会发现到找出解题的突破口非常关键[1].基于此，本文中借助几道例题分析“角平分线”对初中几何解题思路探究发挥的作用，希望对一线教师有所启发.

2 例题引入，思路探究

例1如图1，已知在Rt△ABC中，∠ACB=90°，∠B=60°，AD平分∠BAC，CE平分∠BCA，AD与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为点M，N.求证：FE=FD.

图1

分析：本题可根据题目已知条件及角平分线定理作出点F到AC的距离，如图2所示.然后，通过FN的“桥梁”作用证明FM=FN.最后，在证明△FME和△FND全等的基础上得到FE=FD.

证明：如图2所示，过点F作AC的垂线，垂足为H.

∵AD平分∠BAC，CE平分∠BCA，且FM⊥AB，FN⊥BC，

∴MF=FH=NF.

∵∠ACB=90°，∠B=60°，

∴∠MEF=75°，∠FDN=75°.

∴△FME≌△FND(AAS).

∴FE=FD.

图2

例2已知：如图3所示，在△ABC中，∠C=90°，∠B=30°，AD是∠BAC的角平分线.求证：BD=2CD.

图3

图4

分析：本题条件不多，对寻找解题突破口最有帮助的是“AD是∠BAC的角平分线”这个条件.这类题和角平分线的性质有关，常结合等腰三角形、垂直平分线、直角三角形30°角的性质定理等知识，相对比较基础.

证明一：∵∠C=90°，∠B=30°，

∴∠BAC=60°.

∵AD是∠BAC的角平分线,

∴∠BAD=∠CAD=30°.

∴BD=AD，AD=2CD.

∴BD=2CD.

证明二：如图4，过点D作AB的垂线，垂足为点E.

∵AD是∠BAC的角平分线，

∴CD=ED，∠BAD=∠CAD.

∵∠C=90°，∠B=30°，

∴∠BAC=60°.

∴∠BAD=30°.

∴AD=2ED.

∵∠B=∠BAD=30°，

∴BD=2ED.

∴BD=2CD.

例3已知：如图5所示，△ABC的外角∠CBD和∠BCE的角平分线分别是BF，CF，且这两条角平分线相交于点F.求证：点F在∠DAE的角平分线上.

图5

分析：本题给出的条件非常少，但当已知角平分线时，不妨将角平分线上的点到角的两边的垂线段作出来，然后结合“角平分线的判定定理”证明“点F在∠DAE的平分线上”.但是，要注意说明点F在∠DAE的内部，这是角平分线判定定理使用的前提.由此可见，抓住“角平分线”这个关键条件并借助它的性质解决问题非常重要.

证明：如图6所示，过点F分别作AD，BC，AE的垂线，垂足分别为点G，H，M，连接AF.

∵BF和FC分别是△ABC的外角∠CBD和∠BCE的角平分线，

∴GF=HF=MF.

∵点F在∠DAE的内部，

∴点F在∠DAE的角平分线上.

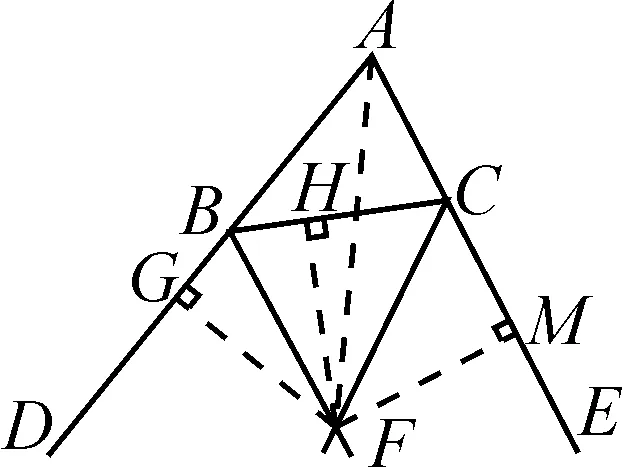
图6

3 总结经验，发挥作用

通过以上三道例题的分析不难发现，“角平分线”这个条件一旦题中给出，那么常会对解题发挥如下作用.

首先，引导思路.“角平分线”的出现让学生的解题思路不知不觉倾向于与之有关的性质定理和判定定理，而这些都与“点到角的两边的距离相等”有关[2].所以，这就提醒学生需要作出与“点到角的两边的距离”有关的辅助线.但是，这里的辅助线通常有两种情况：第一，题中已经给出了“点到角的一边的距离”，需要再作出与“点到角的另一边的距离”有关的垂线段，如例1、例2都是如此；第二，题中只已知角平分线，但这个点到角任何一边的距离是未知的，此时需要将点到角的两边的垂线段都作出，如例3便是如此.

其次，变中有定，训练思维.题中作辅助线的方式虽然有差异，但是证明过程具有相同点，即发挥等量代换的作用实现三角形全等的证明.这主要表现在以下两个方面(以上述题目为例)：第一，都利用了“等量代换”.如例1中通过“FM=FH，FH=FN”中的FN起到“桥梁”作用，证明了FM=FN；如例2中可将“BD=2DE”的“DE”根据“DE=CD”代换，最终得到“BD=2CD”；再如例3中通过“FG=FH，FH=FM”证明了FG=FM.第二，都可用“全等三角形”证明.由此可见，“角平分线”和“全等三角形”具有非常密切的联系[3].

最后，构建知识网络.角平分线和垂直平分线在初中几何题中同时出现的可能性非常大，而这“两线”无论是定义、性质、判定，还是尺规作图的方法都非常相似，学生在学习时极易混淆.但是，角平分线的出现，常让学生联想到垂直平分线，从而将二者联系起来，从而构建更丰富、完善的知识网络体系[4].例如，学生在题中接触了角平分线后，由角平分线的性质、判定联想到垂直平分线的性质、判定，或者联想到它们的尺规作图方法，从而衍生出类似的思维导图.一旦这样的思维导图建立，那么学生就能从一个“点”出发联想到更多的“点”，而点与点之间往往可构成知识网络.所以，作为初中数学教师有必要在角平分线出现的同时，将之与垂直平分线联系起来，从而给予学生更多构建知识网络的机会，让他们更灵活地掌握和运用知识.

4 结语

总之，若题中给出了“角平分线”这个条件，那么它将对这道题解题思路的探究发挥积极的作用.学生要在熟练掌握角平分线性质定理和判定定理的基础上，灵活作出点到角平分线的距离的辅助线，以此找到解决问题的突破口.