例谈与反比例函数有关的图形面积问题

⦿湖北省建始县教学研究室 李翠芝

1 引言

反比例函数的学习是初中数学的一大难点，也是重点，是每年必考的内容.而数形结合思想是解决初中数学问题最重要、最基础的数学思想方法.如,借助数轴求不等式组的解集、借助画线段图解行程问题等都是运用数形结合思想.解决与反比例函数有关的图形面积问题时,如果我们也能运用数形结合思想,往往可以使复杂的问题简单化.下面举例说明.

2 基础题型

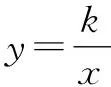
图1

图2

3 简单应用

解析：S△POB=S△POA-S△BOA

图3

图4

图5

解析：如图4,连接OA,OB，则

S△ABC=S△ABO=S△AOD-S△BOD

所以，k1-k2=6.故填：6.

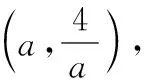
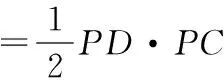
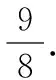
4 常考类型——与中点相关

这类题主要是利用线段的中点得到图形之间的面积关系，一般只需直接应用k的几何意义求解，但有时设坐标求解也比较简单.

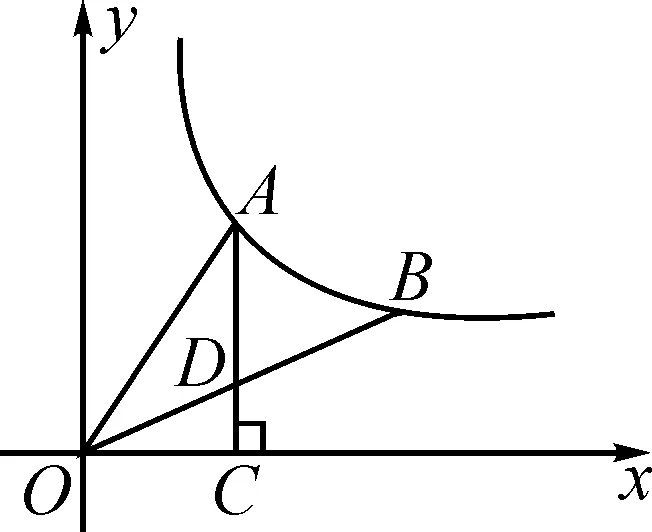
图6

图7

故选：B.

点评：此题也可以设A,D,B中任意一点的坐标，表示出另外两点的坐标，再根据面积求解.

图8

解析：如图9，过点E作EF垂直于y轴于点F.

图9

易证△OEF∽△OBC.由中点条件易得

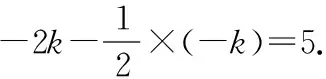
图10

分析：此题的矩形和三角形顶点都不在原点，不能直接用k值表示图形面积，适合设坐标求解.

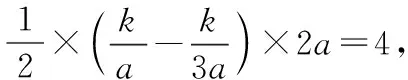
故选：D.

5 直击中考——综合题举例

(1)求经过点B的反比例函数解析式；

图11

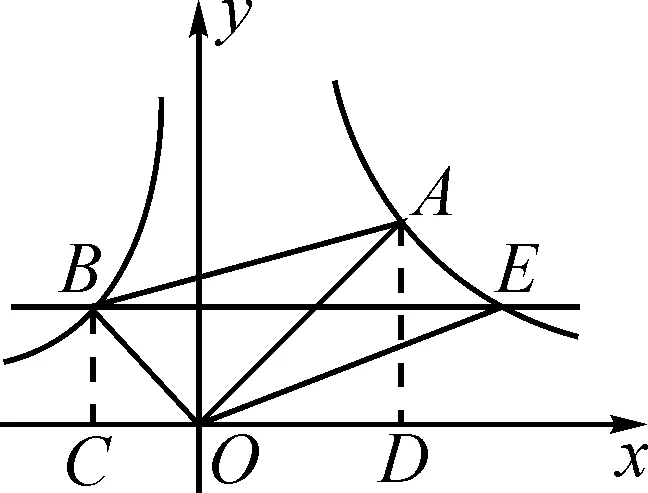
图12

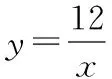
点评：第(1)问也可设点A的坐标，利用三角形相似，由线段之间的关系表示出点B的坐标再求函数关系式.写反比例函数关系式时要注意k值的正负.第(2)问的解答要过点E作x轴的垂线,关键是把求三角形的面积转化成直角梯形的面积问题.

6 结语

综上所述，在解与反比例函数有关的图形面积问题时,一般有两种途径：一是直接利用反比例函数解析式中k的值求解;二是利用函数解析式和图形中的点之间的特殊关系巧设点的坐标求解.即要解决形的问题,我们抓住形的特征,以及形和数之间的特殊关系,把形的问题直接转化成数的问题来求解.这里转化的桥梁就是反比例函数图象上点的坐标.