基于数学思维构建的课堂生成探索——以“平面直角坐标系”的概念教学为例

⦿江苏省滨海县第一初级中学 陈月玲

1 引言

数学思维，顾名思义就是用数学的相关知识去思考问题和解决问题的思维活动形式.心理学认为：“思维是指人脑对客观现实的概括和间接反映，属于人脑的基本活动形式.”而数学思维是逻辑性极强的思维，涵盖了转化与化归，从一般到特殊、特殊到一般，函数与映射的思想，等等.一般来说数学思维能力主要体现在两种能力上，一是联想力，二是数字敏感度.数字敏感度是人从数字的视角认识事物，主要是用数字对事物进行的记忆、辨识的能力，是与生俱来的，与数学的功底无关；而联想力则是“求异思维”或是“多向思维”，属于发散思维的范畴.帮助学生形成联想力是数学思维构建的关键所在，本文中就以“平面直角坐标系”的概念教学为例，谈一谈基于数学思维构建的课堂生成探索.

既然帮助学生形成联想力是数学思维构建的关键所在，那么，数学的联想力又是什么呢？联想力是从给定的一个数学目标出发，用已学的知识通过多种不同的思考途径去探求多种答案的思维方法.在学生的学习中，联想力可以简单地理解为从问题的基本点出发，沿着不同的方向寻求多种解答方法的思维形式，不拘泥于传统的定式做法，有更多的创造性.联想力具有流畅性、变通性和创新性的特点.

2 悉心创设联想力的目标情境

联想力是创造能力的动力源泉，是帮助学生树立创新意识的关键所在[1].为了适应社会的发展，初中阶段的数学教育应当以注重学生良好个性品质和创新思维的构建为根本.作为初中数学的课堂教学，教师应当有意识、有目的地充分应用各种方式对学生进行发散思维的训练，并着重体现在训练学生联想力的流畅性、变通性和创新性等方面.那么教师如何有意识、有目的地在数学教学中培养学生的联想力呢？

例如，苏教版初中数学八年级上册“5.2平面直角坐标系”这一节中，“平面直角坐标系”的内容是学习函数及其图象、曲线和方程的基础，是沟通数与形的纽带.因此，这部分内容在初中数学教学中有着举足轻重的作用，为了帮助学生形成一定的联想力，在本节课堂教学中可以创设如下的教学情境.

师：同学们喜欢旅游吗？现在老师就陪伴你们一起去游西湖.在西湖有十处漂亮的风景，如果你是导游，你会如何向“游客们”介绍这几个风景的位置呢？(让学生尽可能给出简洁的方法，并在小组中交流.学生小组讨论，利用“5.1.物体位置的确定”的知识，确定物体的位置.)

师：如果你站在苏堤春晓，请以“苏堤春晓”为原点作两条互相垂直的数轴，一个方格的边长看作一个单位长度，那么你能找到“平湖秋月”的位置吗？在游玩的过程中，以你为中心，你就是“原点”，若你在“三潭印月”，那么“平湖秋月”的位置又在哪里呢？……

(学生进行实践活动，利用已有的知识在数轴上作出相应的点表示物体的位置.)

设计意图：通过确定风景区的原点位置和改变原点的位置，让学生感受利用数轴上的点表示物体位置的过程，体验数轴与直角坐标系是从一维到二维的思维拓展.这一创设情境具有变通性，让学生的思维活动不再局限于某一框架之中，而是能贯通交汇，巧妙地根据自己是“原点”这一已知条件，应用确定物体位置的相关知识圆满解决问题.

3 营造可以激发联想力灵感的课堂氛围

现代教学理念认为，必须把课堂还给学生，以学生为本，教师着力于引导，营造一个师生关系民主和谐的教学氛围.因为民主和谐的课堂氛围，能让学生有一种作为课堂主人的自豪感，更愿意和教师一起融入到教学中.在这种学习氛围中，学生才明白学习的使命，才敢于表达自己不拘一格的见地，激发出联想力的灵感.那么，如何营造一个民主和谐的课堂氛围呢？

例如，在“5.2.平面直角坐标系”的教学知识生成环节，教师可以帮助学生归纳直角坐标系概念的特征(两条数轴互相垂直，原点重合；通常取向右、向上为正方向，单位长度相同等).再引导学生明确点的位置与对应坐标(示范画出直角坐标系，在给定的平面直角坐标系中，根据坐标找到点的位置，反过来根据已知点的位置写出它所对应的坐标).为了内化这部分知识，可以让学生将一个长是4 cm，宽是2 cm的长方形ABCD置于自己建立的直角坐标系中，并写出各点的坐标.

设计意图：这是一个富含联想力的问题情境.从小组讨论后展示的情况看，学生给出的答案五花八门，如图1～3.

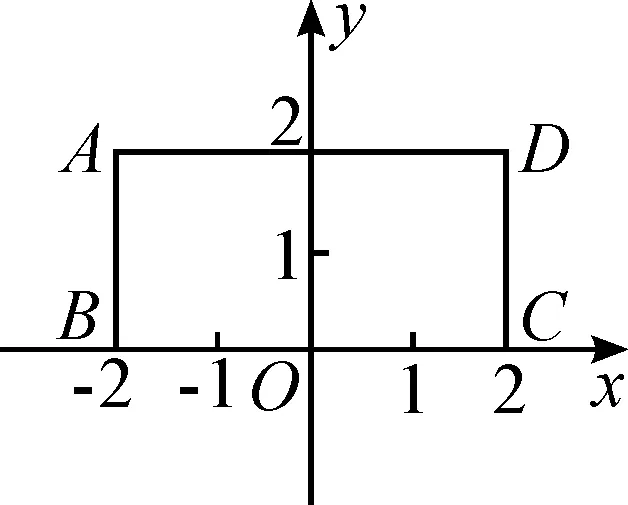
图1

图2

图2

这只展示了一部分答案，还有将长方形的长边放在y轴的.在这个环节，每一个学生都能积极主动地投入到思考、交流、讨论和总结中.尤其是小组合作更利于帮助学生发展团队建设，提升探究实践能力.这种民主和谐的课堂氛围在汇集多种思维的同时，还会碰撞出更多思维的火花，激发出联想力的灵感，这种联想力发展的思维可以让学生获得的成功的体验，增强学习的信心.

4 巧设具有联想力的数学问题变式

众所周知，创新能力是学生在联想力中所做出的不同寻常的、异于常规思路的新奇反应的能力.而创新思维是思维中的最高目标，需要在课堂教学过程中不断地变换知识角度、知识层面.创新思维不仅运用了视觉思维和听觉思维，而且在多重感官的配合下充分接受信息并进行加工，产生联想力.

帮助学生形成具有创新能力的数学联想力，不应采用题海战术，而应该是讲究学习方法，利用多种思维举达到举一反三的效果[2].从学生解决数学问题情况来看，教师需要引导学生对典例“一题多思”，即从不同角度来分析和思考，寻找多种解题方法；同时帮助学生对多种方法进行比较，优化解题思路，总结其内在规律，利用知识进行数学建模.

例如，在“5.2.平面直角坐标系”的教学反思环节，为了让学生能够巩固直角坐标系中点的位置与坐标的关系，在变式练习中创设了“以点O为原点，在直角坐标系中表示出点A在点O的南偏西30°，20 km的位置，并写出点A的坐标”.学生通过解决问题发现“方向与位置”可以表示一个物体在另一个物体的什么位置，点A在点O的南偏西30°，20 km，即是以点O为原点，从南向西(逆时针) 旋转30°，其距离是20 km.通过练习后，有学生大胆地提出，一个风向标和一个旋转就能确定一个物体在另一个物体的什么位置.假如把一个物体放在一点，使用一个数轴和旋转角，也就能够确定另一个物体所在的位置.精彩，这是一种创新思路！

由以上例子不难看出，“一题多思”不在于其方法是否多路径，而在于解决问题后的多反思.经过多反思，一题就可以变成多问，题目还是原来的面目，而达成的结果却是迥然不同，这就是创新.教师在课堂上必须引导学生透过表面看到本质，灵活运用知识解答问题，长久这样善思善问就可以产生“新花样”，让人心花怒放，也就发展了联想力.

5 结束语

总之，联想力是生成数学思维构建的课堂关键之所在.因为联想力中有创新思维的火花，是新时代对创新人才的需要.只要在课堂教学中悉心创设联想力的目标情境，营造可以激发联想力灵感的课堂氛围，巧设具有联想力的数学问题变式，那么就一定可以达成用数学的眼光看待世界的愿景.