“生长数学”:数学课堂教学的愿景
宿迁市苏州外国语学校 费力权
1 引言
著名教育家杜威曾说过:“教育即生长.”教育是为学生的成长而服务的,“学习即生长”也是判断学习成效的标准[1].生长教育强调对教育本质的回归,让教育回归到学科原点,以促进学生更好地生长.如此,我们的数学课堂也应成为数学生长的“摇篮”,学生自然生长的“土壤”.作为教师的我们只有不断为这片土壤注入活水、添加养料,使之不断改良,才能让学生在每个日子里感悟自我生长的内在力量和享受外部生长的阳光雨露.
2 从“问题”中生长思维
问题是数学知识探究的核心本质,也是学生思维的生长点.生长数学的本质,就是让数学教学回归到原点,促进学生的自然生长和必然生长.数学问题的价值在于启迪学生思维,诱导学生积极探索和发现,进而使其学会数学思维,掌握思维方法,实现核心素养的培养.
案例1一元一次方程的认识
在以往的教学中,笔者都是以“年龄问题”进行导入,让学生初步感受从“问题”到“方程”的这一转换过程.然而每次上完课后,都会出现一个共性问题:学生在解决类似问题的过程中,首先就会习惯性地想到用小学数学的代数方法求解,而不是用方程的方法.从学生的共性问题来看,笔者对于问题的设计,相当于直接告诉学生这个问题可以利用列方程的方法来解决,而并未让学生经历从“问题”到“方程”的这一过程.同时,在教学过程中存在两个问题,一是学生在此之前并未接触过方程的概念,二是缺乏用方程来解决问题的经验.在这样的情况下,如何设计问题,才能让学生在问题中生长思维呢?
基于此,笔者在后面执教时,对上述教学做了如下改进:选取学生在小学学习过的“鸡兔同笼”问题进行课堂导入.由于学生已经有解决该问题的经验,所以,提出问题后,首先让学生尽可能地尝试用小学阶段的算术方法进行求解,并对他们的方法进行归纳和总结,指出虽然大家的方法不同,但其数学本质是相同的,那就是“算术法”.在此基础上,向学生提出问题:“我们能否使用假设法的思想,利用字母表示未知数的方法进行求解呢?”
经过这样的引导提问,就有学生提出:假设鸡有x只,兔就有(35-x)只,根据题目中提示“下有九十四足”,就可以列出等式2x+4(35-x)=94.这样就从“算术法”转换为“方程法”,接下来,就是如何求出方程中的未知量的问题了.
在指导学生求出x后,引导学生归纳总结解题的整个过程,让学生明白“假设”的用意,“假设法”迁移变成了“方程法”.这样学生就顺利地实现从“问题”到“方程”的转换,在问题的思考中学生的思维自然得以生长.
3 在“探究”中生长学力
一节数学课应该具有以下几种味道:生活的味道、学科的味道、生长的味道.一节好的数学课都有一个共同的特征就是让学生经历知识的探究过程,并因此喜欢上数学,甚至是迷恋数学,陶醉于每一节数学课,并在数学课上生长学力[2].所谓“学力”指的是知识水平、动手能力和学习能力的总称.而学力的生长,主要源自于课堂上的数学探究,所以,教师在教学中应给予学生充分探究的时间、独立思考的空间,使其体验数学的魅力、成败的乐趣,只有这样才能促使学生的学力走向纵深处.
案例2二元一次方程组的解法2
在课堂教学中,笔者首先以复习导入的方式,帮助学生巩固旧知:
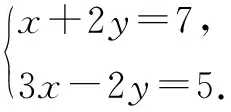
练习2(1)若a=b,c=d,则a+c=.(依据:.)
(2)若3a+b=1,a+2b=2,则4a+3b=.(依据:.)
这两道习题旨在帮助学生复习和巩固代入消元法和等式的性质,从而激活学生已有的知识和经验,加深学生的消元思想,这也正是本节课教学的重点.在此基础上,笔者设计了如下探究活动,为二元一次方程组的解法2探究搭建支架,让学生经历思考、分析、实践和体验的完整学习过程,从而促进学生的学力生长.
活动一:加减法消元.
(1)试一试:认真观察上述练习1中的两个方程,x,y的系数分别是多少?你能试一试如何消元吗?
(2)想一想:如何通过加减消元法求解下面方程组?
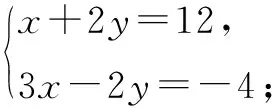
根据你的求解过程归纳总结在方程组①②中何时用相加消元?何时用相减消元?

③和④中何时用相加消元?何时用相减消元?
设计意图:活动一以问题链探究的形式,让学生通过试一试、想一想,观察方程组中系数的特征,思考何时用相加消元,何时用相减消元以及究竟该怎么消元.问题是思维的起点,当学生在这些问题的引导下逐步深入探究时,就会发现新知与旧知之间的联系,有利于发展学生的思维能力和深度学习能力.
活动二:加减消元法一般步骤的探究.
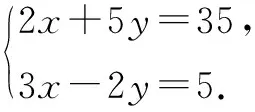
让学生探究例1后,引导学生归纳总结用加减消元法求解二元一次方程组的一般步骤.
设计意图:活动二通过例题的探究,让学生经历知识的发展与形成过程,引导学生从中提炼出一般性的结论,即加减消元法求解二元一次方程组的一般规律和步骤,有利于提升学生思维能力.
活动三:探究合适的方法求解二元一次方程组.
请用合适的方法求解下列二元一次方程组:
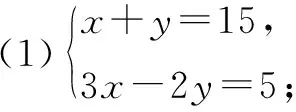
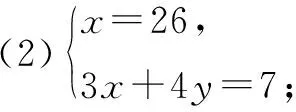

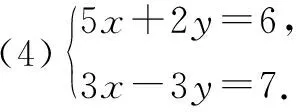
设计意图:活动三设计的目的是让学生通过习题训练,比较两种消元法的差异,感受新知与旧知的异同点,从而加强学生对二元一次方程组解题步骤的理解和认知.
在上述三个探究活动中,让学生经历了利用两种消元法求解二元一次方程组的过程,在促进学生深度思维的同时,也让学生在“探究”中生长了学力,发展了核心素养.
4 结束语
“教育的出发点和落脚点就是让学生经历一种成长、见证一种成长.”这是生长教育的核心本质.生长性数学教学,不需要机械训练题海战术,只需要一点深入一通百通,还能让学生变得更加聪明、理性,且富有科学精神,这也是数学课堂教学的愿景.我们只有立足数学教学的学科本质和高远目标,给学生拾级而上的机会,引导学生开展积极的思维活动,让学生熟练掌握数学核心知识及其关联,领悟数学思想方法,那么,知识、经验、智慧等素养就一定会融入学生的生命成长!

