空气取水系统预冷器遗传算法优化及变工况分析
陈亦涵,胡凌峰,王淑珍,张后雷
(南京理工大学能源与动力工程学院,南京 210094)
我国海岸海岛等地区缺乏淡水资源,获取淡水成为维持此类地区人员生活的重要工作。常用的解决方案包括海水淡化技术、从空气和雾中取水等。本文的研究背景是从空气中取水。典型的空气取水系统基于制冷原理:空气先流经预冷器,再经过蒸发器降温,当温度降低到露点以下时,空气中的水分凝结析出。预冷器的作用是对进入蒸发器之前的空气先进行预冷,可减小蒸发器的制冷负荷,降低制冷装置能耗。预冷器也是整个取水系统的重点研究对象之一。
本文采用重力热管换热器作为预冷器,与其它形式的换热器相比,其优点在于结构简单,加工方便,传热效果好,均温性能显著,冷热流体不易掺混,可实现加热段和冷却段的灵活布置。国内外研究人员对重力热管的传热特性进行了大量实验测试和理论研究,但对其在空气取水系统中的应用则较少涉及。例如,MERT等[1]设计了直径为 25 mm和 40 mm的新型重力热管,研究了风速、空气温度及热源温度对重力热管蒸发段和冷凝段换热性能的影响。HAO等[2]通过实验和数值模拟研究了在 1~4 m/s范围内翅片节距、翅片厚度和翅片类型对重力热管换热性能和压降的影响。
热管换热器设计变量较多,优化方法各异。遗传算法作为一种有效的优化算法,在管壳式换热器和板翅式换热器优化设计中得到了普遍应用,但针对热管换热器的研究则较少。SEPEHR等[3]采用ε-NTU方法对热管换热器进行了建模,并以效率最大化为目标进行了优化,为了保证热管的正常运行,引入热管极限作为约束条件。ZHONG等[4]采用非支配排序遗传算法对重力热管换热器管长、管径和管排数等进行了优化配置,可降低材料消耗和压降,提高热性能。
本文的主要工作是建立预冷器数学模型,采用遗传算法优化预冷器设计,确定最佳设计变量组合,并对初始设计和优化设计预冷器进行相应的变工况分析。
1 预冷器优化数学模型
1.1 几何模型

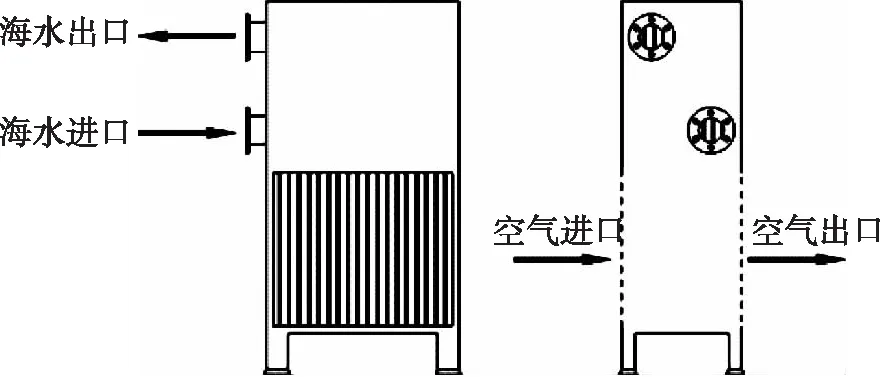
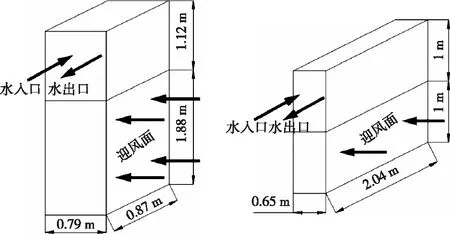
图1 预冷器外形结构
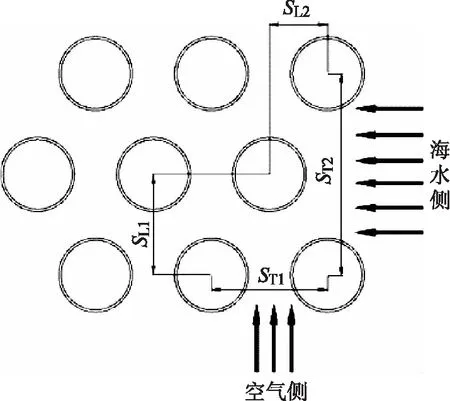
图2 热管布置示意图
1.2 传热模型
预冷器设计计算采用常规工程方法[5]。重力热管的等效热阻网络如图 3 所示。Te为蒸发段管外热流体的定性温度,Tc为冷凝段管外冷流体的定性温度,Tv为管内工质的工作温度。重力热管总热阻包括串联热阻和并联热阻:Rext,e,Rext,c分别为蒸发段和冷凝段管外对流换热热阻;Rwall,e,Rwall,c分别为蒸发段和冷凝段的管壁导热热阻;Rb,e为蒸发段沸腾热阻主要由Rfb,e膜沸腾热阻以及Rpb,e池沸腾热阻组成;Rvapor,n为蒸汽轴向流动热阻;Rcon,c为冷凝段的凝结热阻;Rwall,in为管壁轴向导热热阻。Rvapor,in相对较小,可忽略不计,Rwall,in数值较大,将其所在支路视为开路。由此得到单根热管总热阻简化计算公式为:

图3 重力热管的等效热阻网络图
R=Rext,e+Rext,c+Rwall,e+Rb,e+Rvap,in+Rcon,c+Rwall,c
(1)
总传热系数K的计算以光管外表面积为基准:
1/K=πdolR
(2)
式(2)中,do为管径,m;l为单根热管长度,m;R为单根热管总热阻,K/W。
预冷器总换热量Q、换热面积A及热管总根数n计算如下:
(3)
(4)
(5)
(6)
(7)

空气侧迎风面面积Af1及预冷器管排数B为:
(8)
(9)
(10)
式(8)~(10)中,vf为空气迎面风速,m/s;ρair为空气密度,kg/m3;le为热管蒸发段长度,m;ST1为空气侧热管横向节距,m;n1为迎风面第一排热管的根数。
空气侧和海水侧的总压降ΔP为:
(11)
式(11)中,ΔP1为空气侧压降,Pa;ΔP2为海水侧压降,Pa;Gmax1为空气侧最窄截面处质量流速,kg/(m2·s);vmax2为海水侧最窄截面处流速,m/s;N为海水侧每流程流动方向上的管排数;P为海水侧的流程数;Cf为海水侧阻力修正系数,取值为0.74。
对于等边三角形错排空气横掠圆管,摩擦因子f采用Robinson-Briggs实验关联式[6]:
(12)
式(12)中,Re为空气侧雷诺数。
1.3 约束条件
(1)几何约束条件。管节距大于翅片管外径,即ST>do+ 2Hf,Hf为翅片高度;排节距大于翅片管外径,即SL>do+ 2Hf;翅片节距大于翅片厚度,即lf>δf,δf为翅片厚度。
(2)单根热管换热量约束条件。对于重力热管,携带极限是主要限制,要校核并保证单管最大换热量小于携带极限换热量,当单根热管换热量Qi> 热管极限Qent时,热管不能工作。对于重力式无芯热管,热管的携带极限采用如下公式计算[7]:
(13)
(14)
Bo=dV[g(ρL-ρV)σ-1]1/2
(15)
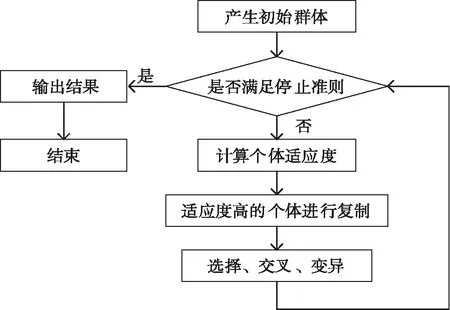
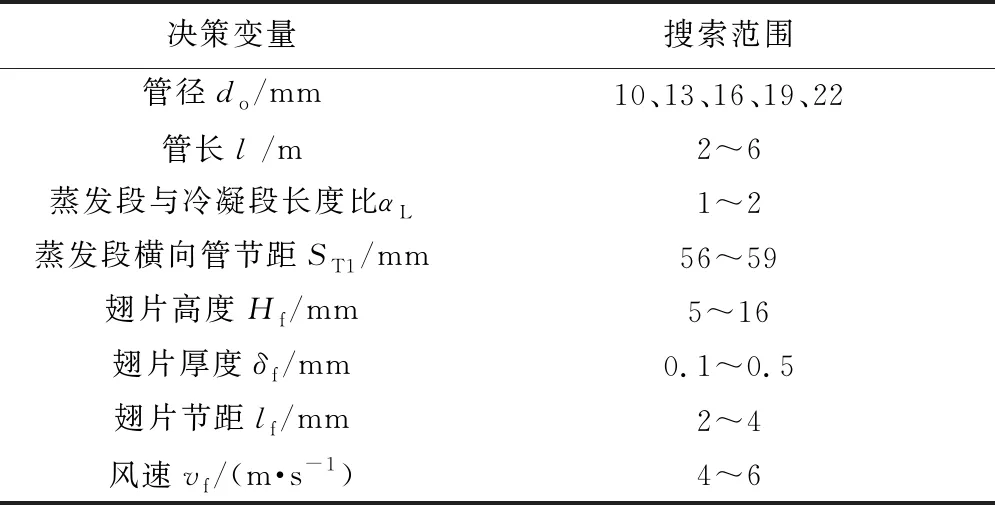
式(13)~(15)中,σ为表面张力系数,N/m;AV为蒸汽流通的横截面积,近似等于管内横截面积,m2;dV为蒸汽流道直径,取管内径,m;Bo为邦德数;ρL为管内工质饱和液密度,kg/m3;ρV为管内工质饱和蒸汽密度,kg/m3;g为重力加速度,m/s2;Ck为系数。在进行遗传算法优化时,不满足Qi 本文采用的遗传算法是一种通过模拟自然界生物遗传和进化过程来完成优化的自适应概率搜索方法[8],其法思路简单,易于实现。当自变量数量较多时,涉及不同参数在取值范围内的随机组合,采用遗传算法可同时兼顾解的质量和求解效率。遗传算法基本流程如图 4 所示,主要包括个体编码、适应度计算、选择、交叉和变异等步骤。本文选取种群规模M= 200;交叉概率Pc=0.8;变异概率Pm=0.07;终止代数iter = 150。 图4 遗传算基本法流程 适应度函数即目标函数,本文以预冷器总功耗为目标函数,包括空气侧的风机功耗和海水侧的泵功耗,适应度函数最小值即要寻找的最优目标函数值: (16) 式(16)中,W1和W2分别为空气侧和海水侧的功耗,kW;qV1和qV2分别为空气侧和海水侧的体积流量,m3/s;ηP1为风机效率,取值为 0.9;ηP2为小型水泵的泵效率,取值为 0.75。 优化时选择管径do、管长l,蒸发段与冷凝段长度比αL、蒸发段横向管节距ST1、翅片高度Hf、翅片厚度δf、翅片节距lf和风速vf等八个变量作为设计变量,组成遗传算法中的个体,目标函数可以表示为W=f(do,l,αL,ST1,Hf,δf,lf,υf),设计变量及范围如表 1 所示。需要说明的是:υf对应气侧迎风面积,当选定l和αL后,υf对应气侧迎风面宽度,因此υf实际上可等效为几何参数。 表1 设计变量及范围 图 5 所示为预冷器的总功耗随遗传代数的变化。由图 5 可见,随着优化过程的进行,功耗逐渐降低。在前 30 代的进化过程中,功耗下降较快且已降低到2.14 kW,此后功耗下降缓慢,进化到 125 代以后基本保持恒定。为提高优化效率并确保计算可靠性,本文只考虑前 200 代的优化结构,超过 200 代数值保持恒定无需计算。图 6 所示为单根热管总热阻随遗传代数的变化。随着优化过程的进行,单根热管总热阻逐渐降低,说明预冷器的换热效果在不断提升。 图5 预冷器的总功耗随遗传代数的变化 图6 单根热管总热阻随遗传代数的变化 预冷器优化结果见表 2 。表 2 中的初始值(初始设计)系在工程经验范围内随机选定[8]。由表 2 可见,空气侧的功耗占总功耗的主要部分,且优化后预冷器的总功耗下降为初始值的 37%。采用遗传算法进行优化的总耗时约为 52 min(电脑配置为Intel-i7 16GB),若采用普通的枚举法,假设忽略连续变量离散化处理而产生的误差,将 8 个变量(包括1个离散型变量管径do和 其它7 个连续型变量)每个变量都取 5 个离散点,则共有 58=390 625种方案,假设每种方案的计算时间为 1 s的量级,则总耗时为 6 510 min的量级,由此可见遗传算法可极大地缩短寻优计算时间。 表2 预冷器优化结果 预冷器优化前的外形尺寸示意图如图 7 所示。初始设计预冷器热管总根数为 272 根,管排数为 17,迎风面第一排管子根数为 16 根,外形尺寸为0.79 m×0.87 m×3 m,总换热面积为(包含翅片)876.1 m2;优化设计预冷器热管总根数为 476 根,管排数为 14,迎风面第一排管子根数为 34 根,外形尺寸为 0.65 m×2.04 m×2 m,总换热面积为(包含翅片)814.8 m2。值得注意的是,优化后的总换热面积较优化前减小了约7%,但热管数量较多。 图7 预冷器优化前的外形尺寸示意图 当环境温度变化时,预冷器进口风温会变化,预冷器负荷(对应风量)也可能会随需求变化。本节对初始设计和优化设计预冷器进行变工况(变进口风温、变风量)分析,其中进口风温变化范围为20~45 ℃,风量变化范围为5~10 kg/s。 进口风温对单根热管换热量和携带极限的影响见图 8 ,由图 8 可见,两种设计的携带极限随Th1的变化不明显。对于初始设计,当Th1>33.4 ℃ 时,单根热管换热量将超出携带极限,热管不能正常工作,见图 8 中(a)部分;对于优化设计,当Th1>35 ℃ 时,单根热管换热量超出携带极限,热管不能正常工作,见图 8 中(b)部分。图 8 的结果表明优化设计对应的进口风温上限略高于初始设计。 图8 进口风温对单根热管换热量和携带极限的影响 进口风温对总换热量的影响如图 9 所示。由图 9 可见,在变风温条件下,两种设计的总换热量基本相等,均随进口风温的升高而线性增大。显然,进口风温增大,换热温差会增大,从而导致换热量增加。进口风温对出口风温和出口水温的影响如图 10 所示。由图 10 可见,当风量保持不变时,两种设计的Th2和Tc2均随Th1的升高而线性升高,且两种设计的变风温特性基本一致。 图9 进口风温对总换热量的影响 图10 进口风温对出口风温和出口水温的影响 进口风温对总功耗的影响如图 11 所示。由图 11 可见,随着Th1的升高,两种设计的W均略有增大,且在整个进口风温范围内,优化设计的总功耗都显著低于初始设计。事实上,由于进口空气流量给定,进口风温增加导致空气密度减小,因此进口风速提高,从而使得空气侧功耗或总功耗增大,但是在给定温度范围内Th1对W的影响较为有限。 图11 进口风温对总功耗的影响 进口风量对单根热管换热量和携带极限的影响如图12所示。由图 12 可见,在 5 kg/s ~ 10 kg/s流量范围内,风量对两种设计的携带极限均无明显影响,单根热管换热量也都小于相应的携带极限,两种设计单根热管换热量均随着流量的增大而增大。事实上,优化设计热管采用了更小的管径,其单根热管换热量和携带极限均小于初始设计;小管径虽然携带极限更低,但小管径热管布管密度更高,即单位体积的换热面积更大。 图12 进口风量对单根热管换热量和携带极限的影响 风量对总换热量的影响如图 13 所示。由图 13 可见,两种设计的总换热量均随风量的增大而增大,且基本无差异。事实上,风量增大意味着风侧换热系数和总传热系数增大,总换热量因此增大。风量对出口风温和出口水温的影响如图 14 所示。由图14可见,当Th1不变时,两种设计的Th2和Tc2均随风量M1的升高而升高,且两种设计基本无差别。 图13 风量对总换热量的影响 图14 风量对出口风温和出口水温的影响 风量对总功耗的影响如图 15 所示。由图 15 可见,风量对两种设计的总功耗具有显著影响。当流量增大时,初始设计比优化设计的总功耗增加得更快,且前者总功耗始终显著高于后者。事实上,风量增加,空气侧压降增大,从而导致总功耗增大,但两种设计的变风量特性(例如,总功耗随风量的变化率)并不一致。 图15 风量对总功耗的影响 本文采用遗传算法对用于空气取水系统的预冷器进行了优化。优化以预冷器运行总功耗最小为目标,涉及管径、管长、蒸发段与冷凝段长度比、横向管节距、翅片高度、翅片厚度、翅片节距、风速等八个设计变量。设计实例表明:与根据工程经验随机选取的初始设计相比,总功耗由 4.9 kW减小到 1.8 kW,下降显著;与普通枚举法优化相比,遗传算法显著缩短了寻优时间,优化时间由普通枚举法的 6 510 min下降到 52 min。 对初始设计和优化设计进行的变工况分析表明:两种设计的总换热量、出口风温和出口水温随进口风温和风量的变化特性基本一致,但优化设计的进口风温上限略高于初始设计,进口风温对两种设计的总功耗影响都较小,而风量对两种设计的总功耗影响都较大,且两种设计的总功耗随风量的变化率明显不同。 本文的优化结果可用于空气取水系统优化设计,所建立的优化模型也可用于其他场合的重力热管换热器设计。2 遗传算法进行热管换热器优化
2.1 算法原理
2.2 适应度函数
2.3 决策变量编码及搜索范围
3 预冷器优化结果与变工况分析
3.1 优化结果
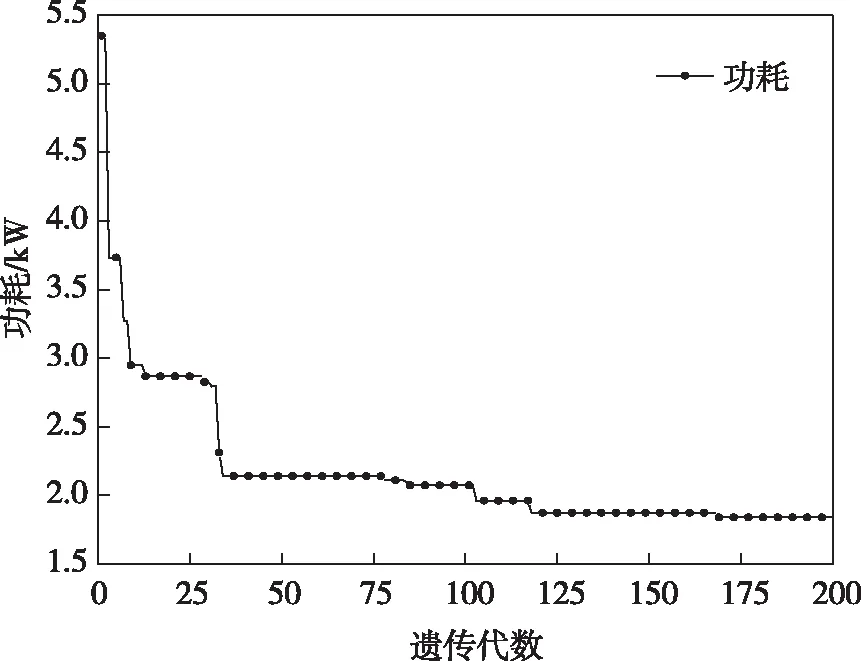


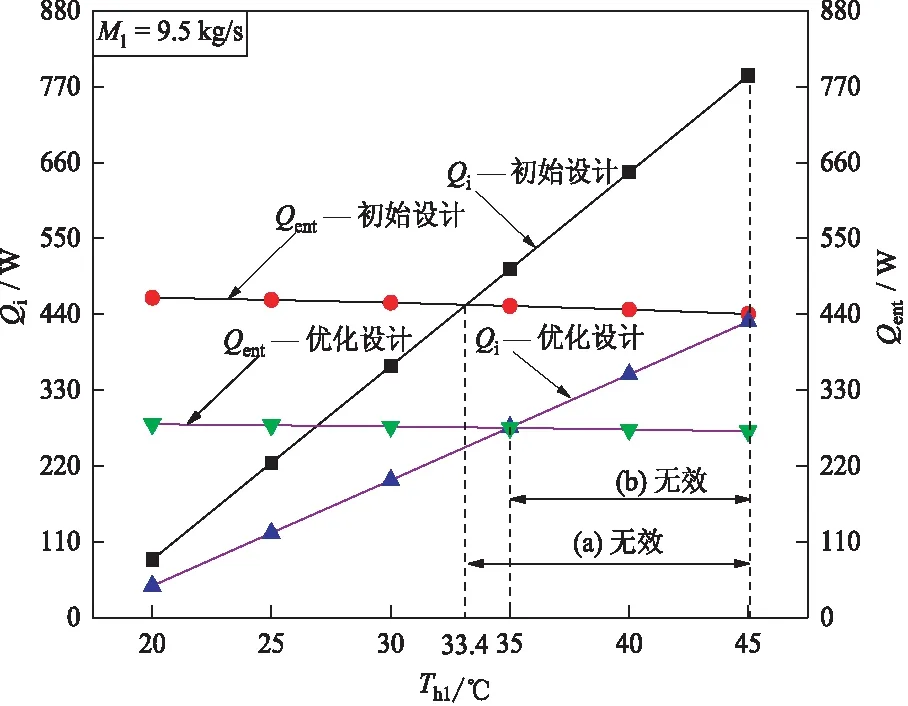
3.2 变工况分析
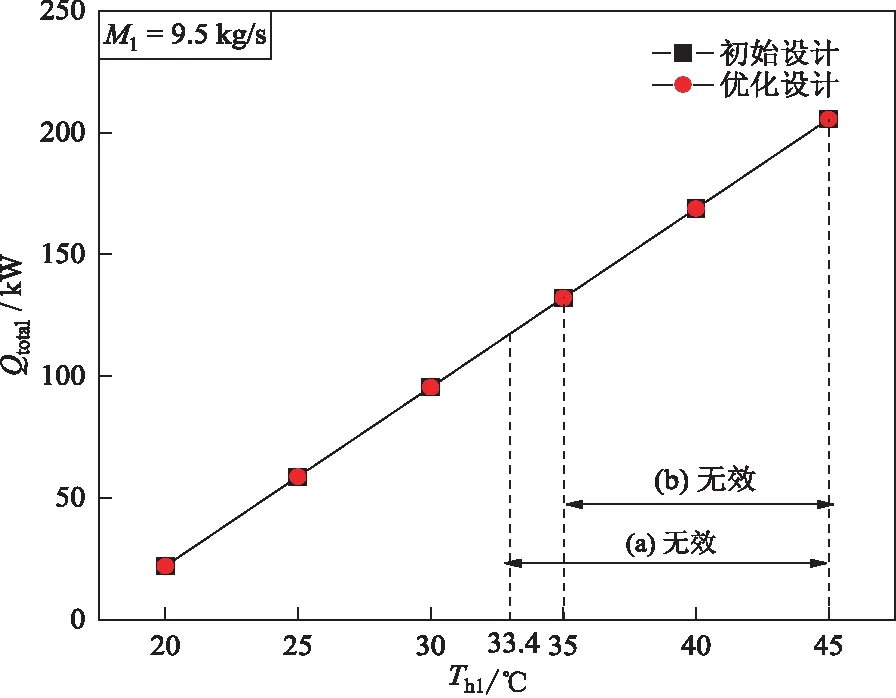


4 结语

