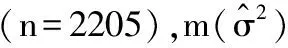基于LS-SVM的时空变系数回归模型算法及仿真

苏磊·乃比，张辉国，胡锡健

(新疆大学数学与系统科学学院，新疆乌鲁木齐市 830046)

1 引言

SVM首先由Vapnik等[7]提出，其主要特点为可以通过引入核函数估计较为复杂的非线性变化趋势，且比起Bagging，岭回归及回归树，SVM具有稀疏化运算，避免维数灾难的优点。Suykens等[8]提出的最小二乘支持向量机(least squares support vector machine，LS-SVM)则是将SVM的二次规划问题转化成线性方程组，大幅度提高了求解的可行性。Quan等[9]建立了一类针对非线性时间序列的加权LS-SVM，并通过仿真模拟证实了其精度高于普通的LS-SVM。Shim和Hwang[10]提出了变系数模型的LS-SVM回归估计方法，并通过三组仿真模拟及一项实证分析证实其处理带有不同变化趋势的回归系数及误差项具有精度高，偏差小的优点。随后Shim和Hwang[11]基于GTWAR模型提出了一类基于SVM核函数的时空加权自回归模型，并通过深圳房价数据将提出的模型与普通最小二乘回归，空间自回归，GWR，GTWAR等模型比较分析，验证了其具有更低的误差，更高的F统计量以更高的决策系数R2。

然而绝大部分空间或时空模型的研究很少涉及将传统回归框架与新兴的机器学习框架结合并通过仿真验证其还原真实系数曲面的能力。本文通过将LS-SVM框架应用于时空变系数回归模型，在保持传统模型的可解释性特征的前提下提高模型精度及灵活性。

2 GTWR模型的介绍

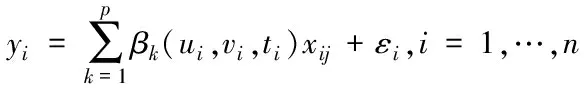
(1)

其中，βk(ui，vi，ti)，k=1，…，p为 (ui，vi，ti)点处的系数函数，εi(i=1，…，n)为均值为0，方差为σ2的独立同分布随机变量。模型允许通过规定xi1=(1，1，…，1)T引入时空变系数截距项β1(ui，vi，ti)。系数函数βj(ui，vi，ti)的估计值可由下式给出：

其中X=(x1，…，xp)，Y=(y1，…，yn)T，时空权重矩阵W(ui，vi，ti)=diag(wi1，…，win)，其对角元素wij(j=1，…，n)为样本点之间的权重函数，可以通过引入以下时空距离确定该权重函数：

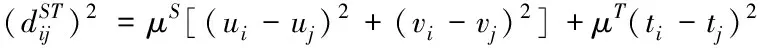
(2)

相应的

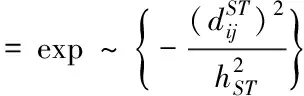
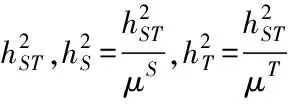
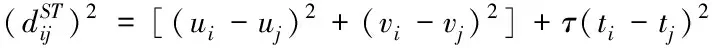
(3)

GTWR模型中的超参数参数一般可通过交叉验证(CV)或赤池信息准则(AIC)等方法选取最有超参数。

3 LSSVM-STVC回归模型

3.1 LSSVM-STVC回归模型及其系数估计

基于文献[10]中的思想，本文假设模型(1)中的时空变系数函数βk(ui，vi，ti)，k=1，…，p与时空坐标(ui，vi，ti)有如下非线性关系

(4)

其中，Φ(ui，vi，ti)为非线性特征映射，其作用是将输入空间映射到更高维(甚至无穷维)特征空间；wj为与特征映射Φ(ui，vi，ti)相应维度的权重向量。于是对于给定样本点(ui，vi，ti，xi)，回归函数可以表示为

根据Mercer[12]，特征映射的内积可以由输入空间的一类核函数表示：

K((ui，vi，ti)，(uj，vj，tj))=Φ(ui，vi，ti)TΦ(uj，vj，tj)

(5)

最常用的核函数之一称之为高斯核函数，其形式如下

Kij=K((ui，vi，ti)，(uj，vj，tj))

基于经典LS-SVM模型，模型(1)对应的优化问题可定义为

i=1，…，n

其中，γ为正则化参数，ei,i=1，…，n为均值为0，方差Var(e)<∞的独立同分布随机误差。通过引入一组拉格朗日乘子αi，i=1，…，n可得以下拉格朗日函数

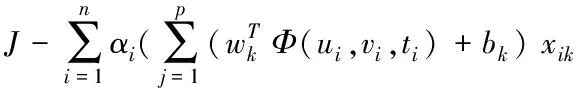
+ei-yi)，i=1，…，n

(6)

于是，原优化问题的KKT条件可以表示为

k=1，…，p，

基于上述，替换wk,k=1，…，p及ei,i=1，…，n，可得以下线性方程组

(7)

其中，X=(x1，…，xp)，Y=(y1，…，yn)T，α=(α1，…，αn)T，b=(b1，…，bj)T，核函数矩阵K由Kij=K((ui，vi，ti)，(uj，vj，tj))组成，Op×p表示p维全0方阵，0p×1为p维全0向量，⊙表示矩阵对应元素相乘。

给定样本点(u0，v0，t0，x0)，LSSVM-STVC回归模型的系数估计为

对应的回归函数的估计值为

3.2 LSSVM-STVC回归模型的参数选择

基于文献[10]中模型选择的思想，本文给出一类适用于LSSVM-STVC回归模型的一类广义交叉验证(GCV)方法。该方法相比较于传统的交叉验证(CV)可大幅度提高运算效率。

假设λ是LSSVM-STVC回归模型的一组超参数(包括核参数κ，τ以及正则化参数γ)，且

=((u1，v1，t1，x1)|λ)，…，(un，vn，tn，xn)|λ))T=HY

其中，H=(XXT⊙K)H0称之为帽子矩阵，且有

及Z=XXT⊙K+(1γ)In，于是可得相应的GCV函数

最优超参数组λ亦选取恰当使得上式取最小值即可。

4 仿真与结果分析

基于本文模型，本节分别设计样本量为n=245及n=2205情形下的仿真，并通过构造合适的统计量对拟合效果进行检验。

给定时空变系数模型(1)，令p=2，xi1≡1 及xi2=xi，i=1，…，n，于是仿真模拟数据可由下式生成

yi=β1(ui，vi，ti)+β2(ui，vi，ti)xi+εi，

i=1，…，n

(8)

其中，解释变量xi，i=1，…，n通过均匀分布U(0，1)随机生成，随机误差项εi，i=1，…，n由正态分布N(0，0.52)随机生成，回归系数βk(u，v，t)，k=1，2分别取定为以下时空非线性及时空线性趋势：

β1(u，v，t)=2sin(πu)exp(-(4-t)/40)

β2(u，v，t)=(u+v)exp(-(4-t)/40)，

其中，对应于每一个时间点t，均有1×1矩形区域内的m×m个空间坐标u和v。根据上式，回归系数βk(u，v，t)，k=1，2值均限定在0到2之间。由上述步骤生成的两个回归系数的初始曲面如图1所示。

为了评价本文模型的拟合优度，以下引入几类统计量。假设响应变量的估计值为

其中H为上一节定义的帽子矩阵。于是残差的样本方差可定义为：

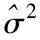
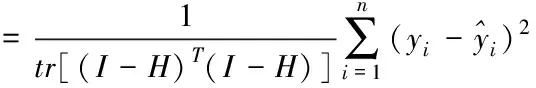
(9)

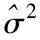
(10)

图1 初始回归系数曲面

对于给定时空坐标点(ui，vi，ti)，第k个回归系数βk(ui，vi，ti)的估计值为：

(11)

(12)

虽然实际问题中真实的βk(ui，vi，ti)往往不是已知的，进而导致MMSEβk无法计算，但是本文设计的仿真模拟实验可以有效地展示在一组同时包含时空线性以及非线性趋势的回归系数下的拟合效果。

实验分别选取样本量为n=245及n=2205的情形来展示本文模型在样本量较小及较大情形下的拟合效果。对于每一个样本量，解释变量x重复随机生成50次，且对于每一次生成的x，误差项随机生成N=100次并计算(8)-(11)式中各统计量。最终结果如表1及图2、3所示。

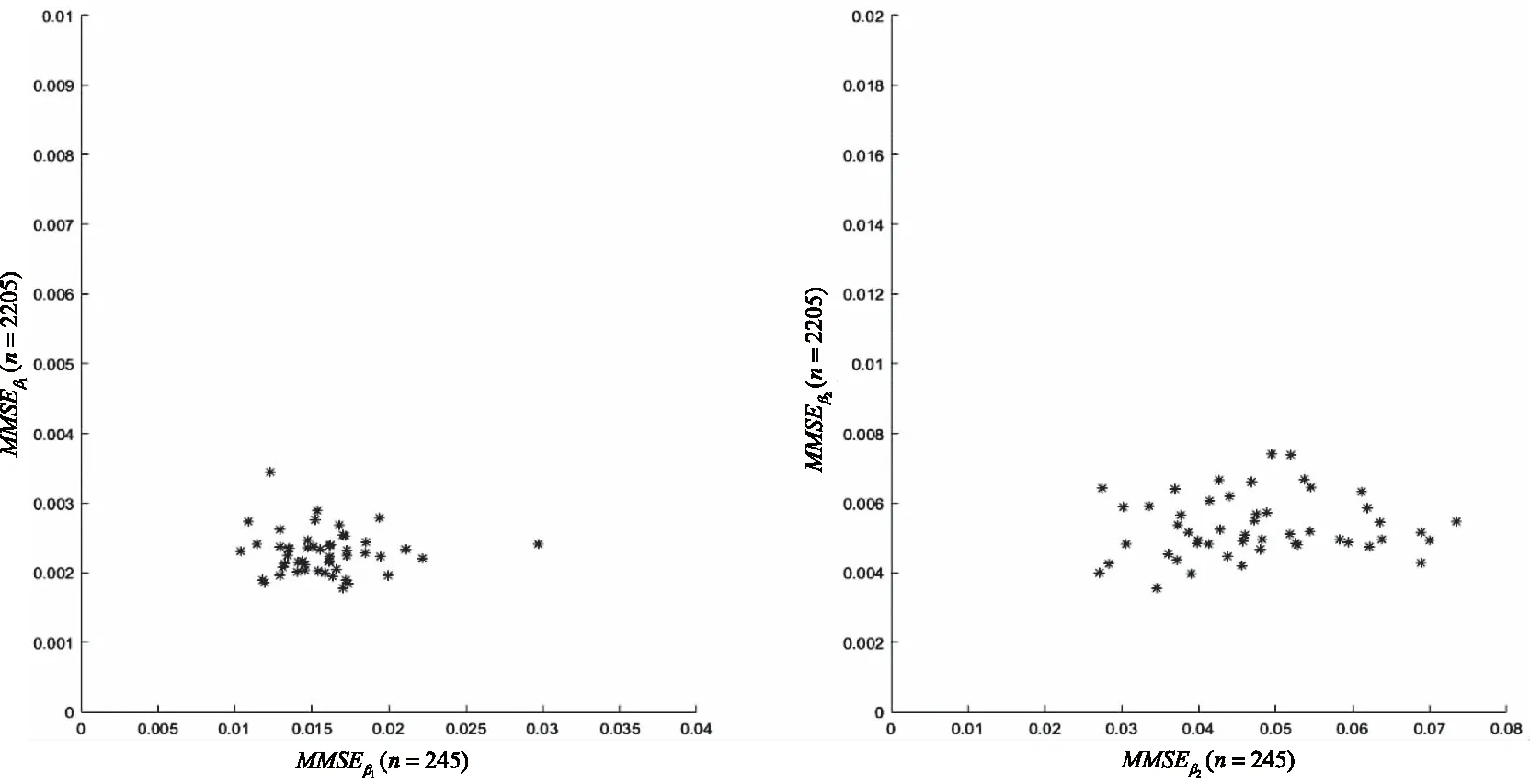
图2 重复试验50次MMSEβ1(左)与MMSEβ2(右)散点图

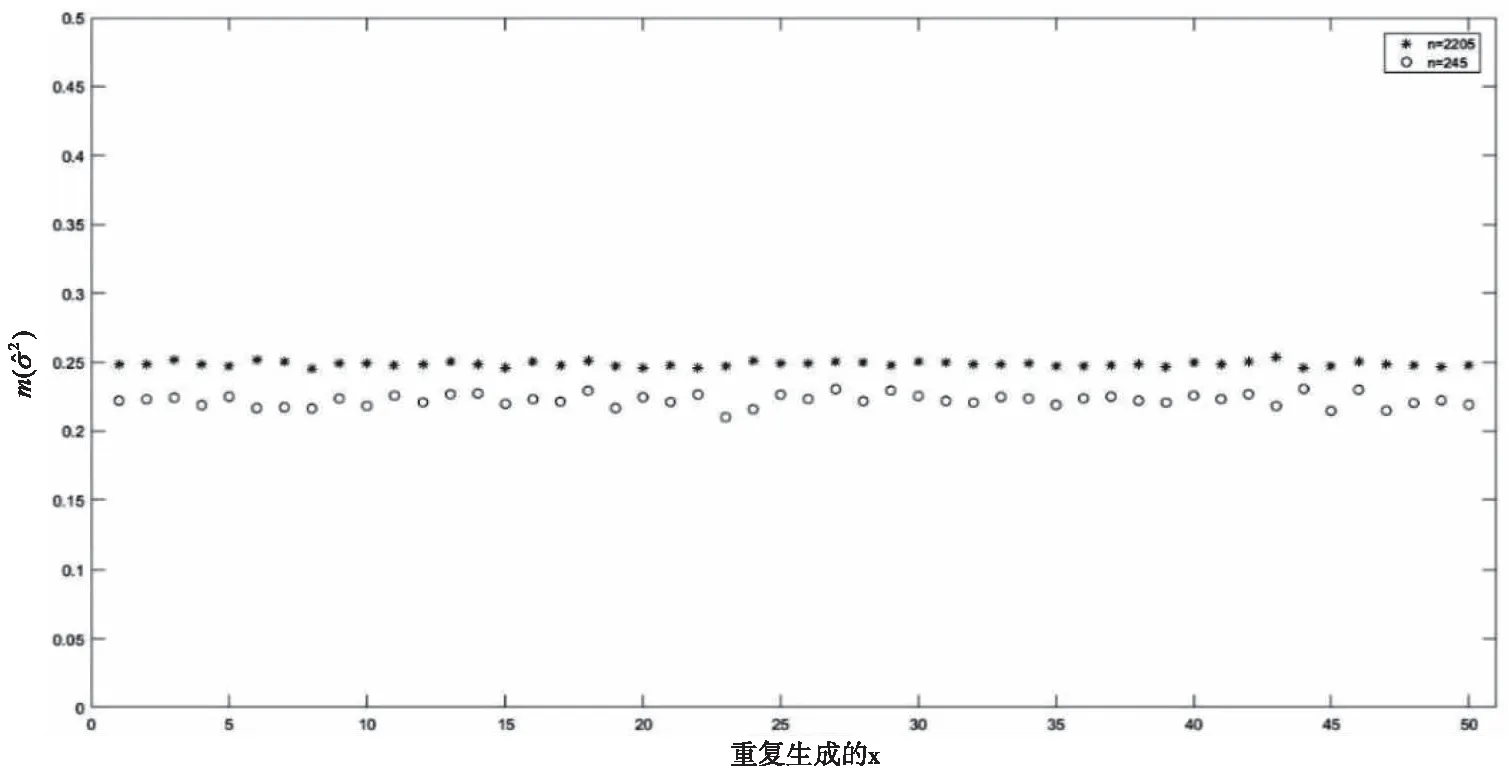
图3 重复试验50次散点图

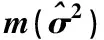
表1 50次重复试验MMSEβk(k=1，2)以及的均值及标准差

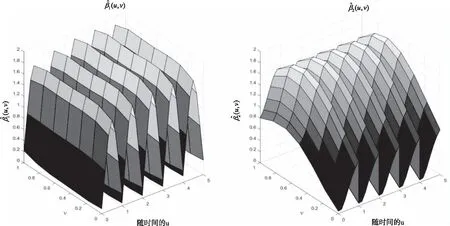
图4 n=245下的m(1 (ui，vi，ti))(左)及m(2 (ui，vi，ti))(左)曲面

图5 n=2205下的m(1 (ui，vi，ti))(左)及m(2 (ui，vi，ti))(左)曲面

5 结论