一种多重影像线特征匹配算法的设计与仿真

崔戈辉，房金谱

(1. 西安工业大学计算机科学与工程学院，陕西 西安 710021；2. 西安工业大学，陕西 西安 710021)

1 引言

在不同类型的影像中均含有大量有价值的几何和语义信息，影像匹配在三维建模中占据重要的地位，影像匹配是指分析两幅图像中相似特征之间的关联性，即求解不同影像之间的几何关系[1，2]。目前，影像匹配已经逐渐发展成为目标图像识别和配准的重要技术之一。和传统的影像相比，多重影像更加复杂，导致进行多重影像线特征匹配存在更大的难度。

为此，各种多重影像线特征匹配方法相继被提出，例如张平等人[3]通过直线检测算法针对参考图像和搜索图像进行直线特征提取，将提取结果进行编码处理，得到对应的直线对。将直线对设定为匹配基元，通过双重核线约束以及最优相似性原则确定同名直线对，对直线对进行拆分处理，同时结合仿射变换过程中不一致的单直线进行整合，获取最终的匹配结果。陈敏等人[4]优先分析不同直线特征之间的几何关系，构建特征区域和对应的描述符，采用双向匹配策略对图像直线特征进行初始匹配。结合初始匹配结果建立影像基础矩阵，同时借助自适应特征进行二次匹配。在设定的自适应特征区域内，提取影像内容一致的特征区域，获取相似特征描述符，完成特征点自适应匹配。

由于以上两种算法没有对多重影像进行边缘检测，导致匹配结果不理想，匹配效率下降，漏匹配率增加。为此提出一种基于仿射不变性的多重影像线特征匹配算法，经实验测试证明，所提算法能够有效提升匹配效率，降低漏匹配率，获取高精度的匹配结果。

2 多重影像线特征匹配算法

2.1 多重影像边缘检测

对于多重影像{f(x，y)}中的不同像素，需要考虑不同坐标下邻近点灰度的加权和，设定Sobel算子表示为

s(i，j)=|Δxf|+|Δyf|

(1)

式中，s(i，j)代表边缘图像；Δxf和Δyf分别代表不同的卷积算子，详细的表达形式如下

(2)

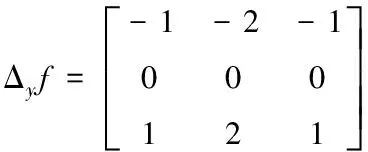
(3)

针对Sobel算子具有较强的方向性等特点，对已有Sobel算子进行改进，详细的操作步骤为：

优先对图像进行全局阈值分割处理，同时进行边缘提取，即可精准检测到多重影像各个方向的边缘[5，6]。经过以上分析，结合边缘提取以及数学形态学理论和方法，对多重影像进行边缘检测，详细的检测流程如图1所示。

图1 多重影像边缘检测流程图

结合图1，优先对多重影像进行阈值处理，主要使用迭代求全局阈值的方法，详细的操作步骤如下所示：

1)设定阈值为T，选取一个与之对应的初始估计值。

2)通过阈值T对多重影像进行分割。

3)计算亮度值G1和高度值G2，设定范围内像素的平均值。

4)计算一个全新的阈值。

5)重复步骤1)到步骤4)，直至满足设定的约束条件。

当得到多重影像的最佳阈值T后，需要对多重影像进行二值化处理，得到经过分割处理后的影像[7，8]。对多重影像进行分割时，会出现将错误背景作为孤立像素的情况。因此，需要将背景中存在的孤立像素全部剔除，然后再进行闭运算。其中，闭运算的基本计算流程为：优先对多重影像进行膨胀；完成膨胀后再对其进行腐蚀，将影像中存在的小裂缝进行拟合，确保目标的位置和形状不发生任何改变。

通过上述分析，能够直接得到一个可以进行目标边缘检测的目标影像。通过Sobel算子实现目标影像的边缘检测，采用A表示。另外一幅多重目标影像需要先对其中一个阈值进行分割，然后再通过Sobel算子进行一次边缘检测，采用B表示。将两幅影像加以相加，即可获取一幅完成边缘检测的多重影像。

2.2 基于仿射不变的多重影像线特征提取

针对目标区域内的不同影像分别采取不同的分割方式进行划分，将梯度方向相同的点统一放置在一个支持区域内，同时提取对应的直线，详细的操作流程如下所示：

1)计算多重影像中各个像元对应的幅值以及梯度方向。

2)将梯度方向对应的值域划分为多个较小的区域，将各个区域进行编号。

3)通过连通成分算法将符号相同的邻接点进行连接，组成直线支持区。

4)提取每一个直线区域所对应的直线。

当得到像元的梯度后，可以通过方向的差异，根据一定的规则将多重影像划分为不同的直线支撑区域。将多重影像直线支持区域内的灰度表面借助平面进行展示。其中，平面中的参数是利用最小二乘法加权拟合获取，而且直线的各个面都是相互垂直的。结合2.1小节获取的边缘检测结果，优先提取边缘点所在的直线支持区，同时将全部像元设定为已知变量，通过计算得到不同边缘点的权值。采用最小二乘计算方法对直线支持区内的全部参数进行拟合，得到直线方程。详细的操作步骤如图2所示。

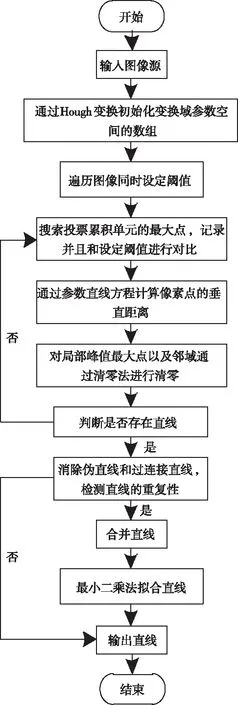
图2 多重影像线特征提取流程图

1)在二值化影像中获取不同坐标点的位置信息，将其存储到对应的二维数据组中。对数组中的全部像素进行遍历处理，得到对应的参数空间矩阵。

2)嵌入清零法的峰值检测：计算多重影像经过Hough变换后矩阵的最大极值点，即局部峰值点。获取该点的取值范围以及坐标位置信息，将其存储到对应的文件夹中。

3)消除伪直线和过连接直线：设定直线连接的最小间隔和检测直线的最小长度，结合两者的取值设定阈值，通过阈值进行伪直线和过连接直线的消除工作。

4)直线合并：由于直线本身具有长度和角度等多种不同的几何属性，所以在进行直线检测的过程中，需要结合阈值对两条直线之间的角度进行设定，当直线满足设定的约束条件，则将其进行合并。

5)直线拟合：当直线完成合并后，通过最小二乘法进行拟合，同时结合仿射不变特性完成多重影像线特征提取[9，10]。

2.3 多重影像线特征匹配

采用SIFT算子对特征区域进行描述，SIFT算子共包含4个步骤，具体如下所示：

1)尺度空间特征检测：

将原始多重影像和高斯函数两者进行卷积操作，形成高斯尺度空间。同时将卷积结果和邻近层次的卷积结果两者相减，获取DOG金字塔D(x，y，σ)，具体的计算公式为

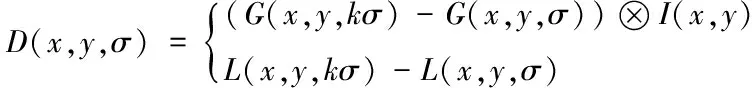
(4)

式中，G(x，y，σ)代表特征描述符；I(x，y)代表原始多重影像；L(x，y，σ)代表经过卷积操作后的多重影像；k代表特征描述符的总数。

2)特征点精确定位：

根据局部极值点对全部函数进行拟合，实现亚像素的精准定位，并且消除外界各种干扰因素带来的不良影响。

3)特征点主方向的计算：

设定邻域中心为特征点，以此为依据计算各个梯度方向的像素值。

4)特征描述符的形成：

设定特征点所在的方向为主方向，其中多重影像以特征点为中心进行旋转。设定中心窗口的大小为16×16，将其划分为4个规格相同的小块，经过计算得到对应的累加值，进而构建128维的SIFT特征向量，即特征描述符。

通过Hesssin-Affine和MSER算法对多重影像中的仿射不变特征进行提取，将目标提取区域进行标准化处理，形成全新的椭圆形区域，采用统一的参数形式进行描述。另外，还需要对得到的区域统一进行归一化处理，形成圆形区域。同时借助SIFT对区域的组成结构进行描述，在此基础上，结合欧式距离进行粗匹配，将匹配不成功的匹配点删除[11]。详细的操作步骤如下所示：

优先通过仿射不变量的方式对特征区域进行转换，形成椭圆区域。结合不同规格MSER特征区域内的像素信息建立二阶中心矩阵，同时将该区域调整为椭圆形区域，如公式(5)所示：

(5)

式中，X代表向量；R代表不规则区域；|R|代表不规则区域内相似像素的总数；E代表中心坐标点；T代表椭圆区域内全部像素点数量。

在上述分析的基础上，需要建立标准的椭圆方程，将两种不同形式的特征参数采用标准化机制进行描述，并且转换为标准的椭圆参数模式。另外，还需要将属性不同的特征进行属性统一。

为了对特征区域进行描述，同时保持原有区域内的内容能够顺利进行传递。结合特征点自相关矩阵M，将特征点xL和xR对应的椭圆区域经过归一化处理形成圆形区域，具体的计算式为

(6)

经过归一化处理后，两个特征区域之间的关系为

xL=RxR

(7)

将Hesssin-Affine和MSER获取的椭圆区域经过归一化处理形成圆形区域，优先通过SIFT计算主方向的方式计算获取各个特征点的主方向，并对多重影像根据特征点进行旋转，保持其旋转不变的特性。结合Hesssin-Affine和MSER特征区域的优势，优先采用SIFT描述目标区域内的全部向量，使多重影像具有旋转不变特性，并且对光照以及噪声等具有较好的抑制作用。所以，无论在任何位置都能够进行精准地匹配。

为了提升匹配结果的准确性，需要通过两个不同的阶段实现。第一阶段将提取的全部多重影像特征向量进行对比，获取可信度最高的匹配点；第二阶段分析不同多重影像之间的约束关系，同时设定约束条件，将不满足需求的特征向量剔除，获取高精度的匹配对。详细的操作步骤如下所示：

1)通过距离相似度的初始匹配：

当得到随机两幅多重影像的特征向量后，在多重影像中任意提取一个特征点，同时获取另外一个影像中相似的特征点。假设第一近距离和第二近距离之间的比例小于阈值，则说明两者是匹配的。另外，多重影像线特征匹配率会随着阈值的降低而增加。

2)基于核线约束的特征匹配：

核线约束在计算机视觉中也可以称为极限几何约束，主要采用基础矩阵F描述任意两幅多重影像之间的核线约束关系。

利用RANSANC算法对各个多重影像之间的关系进行分析，进而获取基本矩阵F，结合矩阵完成基于核线约束的匹配。

3 仿真研究

为了验证所提基于仿射不变性的多重影像线特征匹配算法的有效性，选取文献[3]方法和文献[4]方法作为对比方法，进行仿真实验测试。

为了实现多重影像的匹配，需要对各个算法的匹配性能进行测试，实验优先对比三种不同匹配算法的正确匹配对数量，详细的实验结果如表1所示。

表1 不同视角下的正确匹配对数量

分析表1中的实验数据可知，当视角开始增加，各个方法的正确匹配对数量开始呈下降趋势，但是相比另外两种方法，所提方法的正确匹配对数量明显更高一些。

分析各个方法在不同实验次数下的正确匹配率，详细的实验对比结果如图3所示。

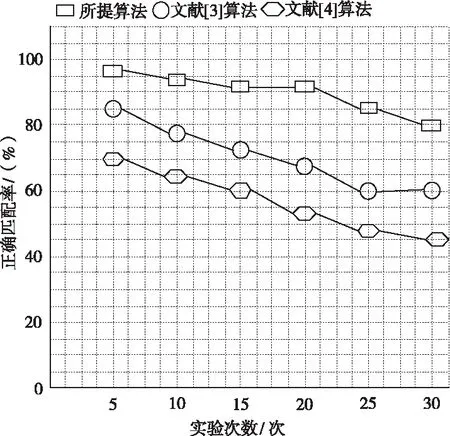
图3 不同算法的正确匹配率仿真测试

分析图3中的实验数据可知，所提算法的匹配结果明显更好，同时具有较高的正确匹配率。

为了更进一步验证所提算法的匹配性能，实验选取一幅多重影像作为测试对象，对各个算法的匹配性能进行测试，详细的实验结果如图4所示。

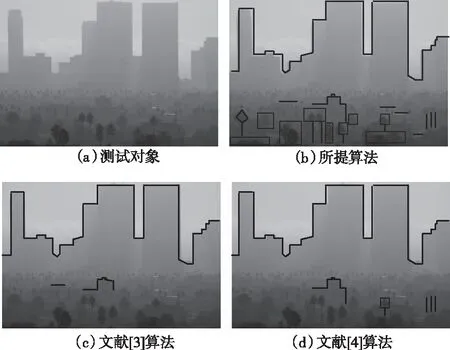
图4 不同算法的匹配结果测试分析

根据图4可知，相比另外两种算法，所提方法能够更加精准提取多重影像的线特征，进而更好地进行线特征匹配，获取满意的匹配结果。

在进行多重影像线特征匹配的过程中，会存在遗漏匹配的情况，以下实验测试将漏匹配率设定为测试指标，详细的实验对比结果如5所示。

图5 不同算法的漏匹配率对比结果

分析图5中的实验数据可知，相比另外两种算法，所提算法的漏匹配率明显更低一些，其漏匹配率始终低于5%。

为了更进一步验证所提算法的有效性，以下测试三种不同算法的匹配效率，详细的实验对比结果如图6所示。

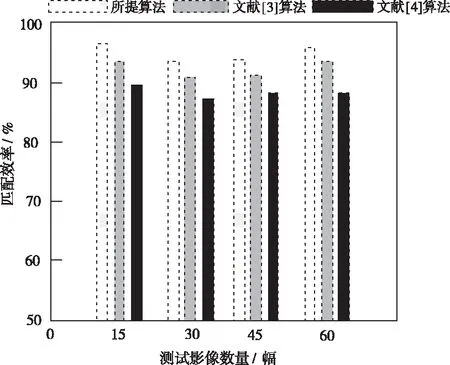
图6 不同算法的匹配效率对比结果

分析图6中的实验数据可知，由于所提算法在进行多重影像线特征匹配之前，对影像进行了边缘检测，并结合边缘检测结果进行特征匹配，能够有效优化特征匹配流程，促使整个算法的匹配效率得到有效提升，明显优于另外两种算法。

4 结束语

多重影像线特征匹配是目前三维重建过程中的难点和热点话题，通过对现有算法的分析和总结，提出一种基于仿射不变性的多重影像线特征匹配算法。实验测试结果表明，所提算法能够有效提升匹配结果的准确性和匹配效率，降低漏匹配率，更好地完成多重影像线特征匹配。

由于研究时间和精力有限，所提算法仍然存在一定的不足，后续将对其展开更加深入地研究。